1.4: 分数

学习目标

在本节结束时，您将能够：

• 简化分数
• 乘以和除以分数
• 加减分数
• 使用运算顺序简化分数
• 使用分数计算变量表达式

可以在基本代数章节 “基础” 中找到对本节所涵盖主题的更详尽的介绍。

简化分数

分数是表示整体各部分的一种方式。 分数\(\frac{2}{3}\)代表三个相等部分中的两个（图\(\PageIndex{1}\)）。 在分数中\(\frac{2}{3}\)，2 被称为分子，3 被称为分母。 这条线被称为分数条。

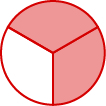
图\(\PageIndex{1}\)：在圆圈中，圆圈\(\frac{2}{3}\)中有阴影——3个相等部分中的2个。

分数

写一个分数\(\dfrac{a}{b}\)，其中\(b\neq 0\)和

\(a\)是分子，\(b\)是分母。

分数代表整体的各个部分。 分母\(b\)是整数被划分为的相等部分的数量，分子\(a\)表示包含了多少个部分。

具有相同值的分数是等效分数。 等效分数

属性允许我们找到等效分数，还可以简化分数。

如果\(a\)\(b\)、和\(c\)是数字\(b\neq 0,c\neq 0\)，其中，

然后还\(\dfrac{a}{b}=\dfrac{a·c}{b·c}\)有\(\dfrac{a·c}{b·c}=\dfrac{a}{b}.\)

如果分数的分子和分母中除了 1 之外没有其他公共因子，则认为该分数是简化的。

例如，

\(\dfrac{2}{3}\)之所以简化，是因为没有\(2\)和的常见因子\(3\)。

\(\dfrac{10}{15}\)未被简化\(5\)，因为是 and 的常见因\(10\)子\(15\)。

我们通过移除分子和分母的共同因子来简化或减少分数。 在移除所有常见因子之前，分数不会被简化。 如果表达式有分数，则在分数被简化之前，它不会被完全简化。

有时候，要找到分子和分母的共同因子可能并不容易。 发生这种情况时，一个好主意是将分子和分母分数分成素数。 然后使用等效分数属性除去常见因子。

简化\(\dfrac{−315}{770}\)。

回答

简化\(−\dfrac{69}{120}\)。

回答

\(−\dfrac{23}{40}\)

示例\(\PageIndex{3}\)

简化\(−\dfrac{120}{192}\)。

回答

\(−\dfrac{5}{8}\)

现在，我们总结了简化分数时应遵循的步骤。

简化一小部分。

1. 重写分子和分母以显示常见因子。
   如果需要，先将分子和分母分数分成素数。
2. 通过除去常见因子来简化等效分数属性的使用。
3. 将所有剩余因子相乘。

乘以和除以分数

许多人发现乘以和除分数比加减分数容易。

要乘以分数，我们将分子相乘，然后乘以分母。

分数乘法

如果\(a\)、\(b\)\(c\)、和\(d\)是数字，其中\(b≠0\)、和\(d≠0\)，那么

\[\frac{a}{b}·\frac{c}{d}=\frac{ac}{bd}\]

要乘以分数，请将分子相乘并乘以分母。

当然，当乘以分数时，正数和负数的属性仍然适用。 作为第一步确定产品的标志是个好主意。 在示例中，我们将乘以负数和正数，因此乘积将为负。

将分数乘以整数时，将整数写成分数可能会有所帮助。 任何整数 a 都可以写成\(\dfrac{a}{1}\)。 所以，例如，\(3=\dfrac{3}{1}\)。

练习\(\PageIndex{4}\)

乘以：\(−\dfrac{12}{5}(−20x).\)

回答

第一步是找到产品的标志。 由于迹象相同，因此该产品为阳性。

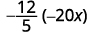
确定产品的标志。 迹象相同，因此产品为阳性。
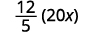
将 20 x 写成分数。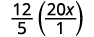
乘以。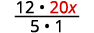
重写 20 以显示公因子 5 并将其除去。
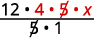
简化。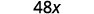

练习\(\PageIndex{5}\)

乘以：\(\dfrac{1}{13}(−9a)\)。

回答

\(−33a\)

练习\(\PageIndex{6}\)

乘以：\(\dfrac{13}{7}(−14b)\)。

回答

\(−26b\)

现在我们知道如何乘以分数，我们差不多可以分数了。 在做到这一点之前，我们需要一些词汇。 分数的倒数是通过反转分数，将分子放在分母中，将分母放在分子中来得出的。 的倒数\(\frac{2}{3}\)是\(\frac{3}{2}\)。 由于 4 以分数形式写成\(\frac{4}{1}\)，因此 4 的倒数为\(\frac{1}{4}\)。

要除以分数，我们将第一个分数乘以第二个分数的倒数。

分数除法

如果\(a\)\(b\)、\(c\)、和\(d\)是数字\(b≠0\)，其中\(c≠0\)、和\(d≠0\)，那么

\[\frac{a}{b}÷\frac{c}{d}=\frac{a}{b}⋅\frac{d}{c}\]

要除以分数，我们将第一个分数乘以第二个分数的倒数。

我们需要说\(b≠0\)\(c≠0\)、和\(d≠0\)，以确保我们不会除以零！

练习\(\PageIndex{7}\)

找出商数：\(−\dfrac{7}{18}÷(−\dfrac{14}{27}).\)

回答

	\(−\dfrac{7}{18}÷(−\dfrac{14}{27})\)
要除以，请将第一个分数乘以第二个分数的倒数。
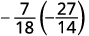
确定产品的符号，然后乘以。
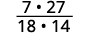
重写显示常见因素。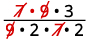
移除常见因素。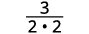
简化。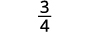

除以：\(−\dfrac{7}{27}÷(−\dfrac{35}{36})\)。

回答

\(\dfrac{4}{15}\)

练习\(\PageIndex{9}\)

除以：\(−\dfrac{5}{14}÷(−\dfrac{15}{28}).\)

回答

\(\dfrac{2}{3}\)

某些分数的分子或分母本身包含分数。 分子或分母是分数的分数称为复数分数。

定义：复杂分数

复数分数是其中分子或分母包含分数的分数。

复杂分数的一些例子是：

\[\dfrac{\frac{6}{7}}{3} \quad \dfrac{\frac{3}{4}}{\frac{5}{8}} \quad \dfrac{\frac{x}{2}}{ \frac{5}{6}}\]

要简化复杂分数，请记住分数条表示除法。 例如，复数分数\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\)意味着\(\dfrac{3}{4}÷\frac{5}{8}.\)

练习\(\PageIndex{10}\)

简化：\(\dfrac{\dfrac{x}{2}}{ \dfrac{xy}{6}}\)。

回答

\(\begin{array}{lc} \text{} & \dfrac{\dfrac{x}{2}}{ \dfrac{xy}{6}} \\[6pt] \text{Rewrite as division.} & \dfrac{x}{2}÷\dfrac{xy}{6} \\[6pt] \text{Multiply the first fraction by the reciprocal of the second.} & \dfrac{x}{2}·\dfrac{6}{xy} \\[6pt] \text{Multiply.} & \dfrac{x·6}{2·xy} \\[6pt] \text{Look for common factors.} & \dfrac{ \cancel{x}·3·\cancel{2}}{\cancel{2}·\cancel{x}·y} \\[6pt] \text{Divide common factors and simplify.} & \dfrac{3}{y} \end{array}\)

简化：\(\dfrac{\dfrac{a}{8}}{ \dfrac{ab}{6}}\)。

回答

\(\dfrac{3}{4b}\)

简化：\(\dfrac{\dfrac{p}{2}}{ \dfrac{pq}{8}}\)。

回答

\(\dfrac{4}{q}\)

加减分数

当我们乘以分数时，我们只是将分子相乘，然后将分母直接相乘。 要加上或减去分数，它们必须有一个公分母。

分数加法和减法

如果\(a\)\(b\)、和\(c\)是数字，其中\(c≠0\)，那么

\[\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \text{ and } \dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\]

要加上或减去分数，请将分子相加或减去，然后将结果置于公分母之上。

两个分数的最小公分母 (LCD) 是可用作分数公分母的最小数字。 两个分数的 LCD 是其分母的最小公倍数 (LCM)。

最小公分母

两个分数的最小公分母 (LCD) 是其分母的最小公倍数 (LCM)。

在我们找到两个分数的最小公分母之后，我们将这些分数转换为使用 LCD 的等效分数。 将这些步骤组合在一起可以让我们加上和减去分数，因为它们的分母将是一样的！

示例\(\PageIndex{13}\): How to Add or Subtract Fractions

添加：\(\dfrac{7}{12}+\dfrac{5}{18}\)。

回答

示例\(\PageIndex{14}\)

添加：\(\dfrac{7}{12}+\dfrac{11}{15}\)。

回答

\(\dfrac{79}{60}\)

示例\(\PageIndex{15}\)

添加：\(\dfrac{13}{15}+\dfrac{17}{20}\)。

回答

\(\dfrac{103}{60}\)

加上或减去分数。

1. 他们有共同点吗？
   • 是-转到步骤 2。
   • 否-使用 LCD（最小公分母）重写每个分数。
     • 找到液晶屏。
     • 将每个分数更改为等效分数，以 LCD 为其分母。
2. 加上或减去分数。
3. 尽可能简化。

现在，我们有了分数的所有四个运算。 该@@ 表汇总了分数运算。

分数乘法	分数除法
\(\dfrac{a}{b}⋅\dfrac{c}{d}=\dfrac{ac}{bd}\)	\(\dfrac{a}{b}÷\dfrac{c}{d}=\dfrac{a}{b}⋅\dfrac{d}{c}\)
将分子相乘然后乘以分母	将第一个分数乘以第二个分数的倒数。
分数加法	分数减法
\(\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c}\)	\(\dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\)
将分子相加，然后将总和放在公分母上。	减去分子，然后将差值放在公分母上。
要乘以或除以分数，不需要使用液晶屏。 要加上或减去分数，需要使用液晶显示屏。

开始练习时，请务必确定该操作，然后回忆该操作所需的方法。

简化：ⓐ\(\dfrac{5x}{6}−\dfrac{3}{10}\) ⓑ\(\dfrac{5x}{6}·\dfrac{3}{10}\)。

回答

首先问：“手术是什么？” 识别操作将决定我们是否需要一个共同点。 请记住，我们需要一个公分母来加或减，但不是乘法或除法。

ⓐ

\ (\ begin {array} {lc}\ text {操作是什么？ 运算是减法。}\\ [6pt]\ text {分数有共同分母吗？ 没有。} &\ dfrac {5x} {6} −\ dfrac {3} {10}\\ [6pt]\ text {查找} 6\ text {和} 10 &\ text {液晶屏是 30。}\\ [6pt] {\\ 3\\\ [6pt]
\;\ 下划线 {\;\;\;\\;\;\;} &\ 下划线 {=2·5\;\;\;\;}\;\\ [6pt]
\ text {LCD} & =2·3·5\\ [6pt]
\ text {LCD} & =30\ end {align*}}\\ [6pt]\\\\
\ text {使用 LCD 将每个分数重写为等效分数。} &\ dfrac {5x·5} {6·5} −\ dfrac {3·3} {10·3}\\ [6pt]
\ text {} &\ dfrac {25x} {30}\\ [6pt]
\ text {减去分子然后将}\\ [6pt]
\ text {差异放在普通值分母。} &\ dfrac {25x−9} {30}\\ [6pt]\\\\
\ text {如果可能的话简化。没有常见的因素。}\\ [6pt]
\ text {分数被简化了。} \ end {array}\)

ⓑ

\(\begin{array}{lc} \text{What is the operation? Multiplication.} & \dfrac{25x}{6}·\dfrac{3}{10} \\ \text{To multiply fractions,multiply the numerators} \\ \text{and multiply the denominators.} & \dfrac{25x·3}{6·10} \\ \text{Rewrite, showing common factors.} \\ \text{Remove common factors.} & \dfrac{\cancel{5} x · \cancel{3}}{2·\cancel{3}·2·\cancel{5}} \\ \text{Simplify.} & \dfrac{x}{4} \end{array}\)

注意，我们需要一个液晶显示器来添加\(\dfrac{25x}{6}−\dfrac{3}{10}\)，但不是要乘以\(\dfrac{25x}{6}⋅\dfrac{3}{10}\)。

示例\(\PageIndex{17}\)

简化：ⓐ\(\dfrac{3a}{4}−\dfrac{8}{9}\) ⓑ\(\dfrac{3a}{4}·\dfrac{8}{9}\)。

回答

ⓐ\(\dfrac{27a−32}{36}\) ⓑ\(\dfrac{2a}{3}\)

示例\(\PageIndex{18}\)

简化：ⓐ\(\dfrac{4k}{5}−\dfrac{1}{6}\) ⓑ\(\dfrac{4k}{5}⋅\dfrac{1}{6}\)。

回答

ⓐ\(\dfrac{24k−5}{30}\) ⓑ\(\dfrac{2k}{15}\)

使用运算顺序简化分数

分数中的分数条用作分组符号。 然后，运算顺序告诉我们要简化分子，然后简化分母。 然后我们分开。

使用@@ 分数条简化表达式。

1. 简化分子中的表达式。 简化分母中的表达式。
2. 简化分数。

分数中的负号在哪里？ 通常负号位于分数的前面，但有时您会看到带有负分母的分数，有时会看到带有负分母的分数。 请记住，分数代表除法。 当分子和分母有不同的符号时，商为负数。

\[\dfrac{−1}{3}=−\dfrac{1}{3} \; \; \; \; \; \; \dfrac{\text{negative}}{\text{positive}}=\text{negative}\]

\[\dfrac{1}{−3}=−\dfrac{1}{3} \; \; \; \; \; \; \dfrac{\text{positive}}{\text{negative}}=\text{negative}\]

在分数中放置负号

对于任何正数\(a\)\(b\)和

\[\dfrac{−a}{b}=\dfrac{a}{−b}=−\dfrac{a}{b}\]

示例\(\PageIndex{19}\)

简化：\(\dfrac{4(−3)+6(−2)}{−3(2)−2}\)。

回答

分数条的作用类似于分组符号。 因此，完全分别简化分子和分母。

\(\begin{array}{lc} \text{} & \dfrac{4(−3)+6(−2)}{−3(2)−2} \\[5pt] \text{Multiply.} & \dfrac{−12+(−12)}{−6−2} \\[5pt] \text{Simplify.} & \dfrac{−24}{−8} \\[5pt] \text{Divide.} & 3 \end{array}\)

示例\(\PageIndex{20}\)

简化：\(\dfrac{8(−2)+4(−3)}{−5(2)+3}\)。

回答

4

示例\(\PageIndex{21}\)

简化：\(\dfrac{7(−1)+9(−3)}{−5(3)−2}\)。

回答

2

现在我们来看一下复杂的分数，其中分子或分母包含可以简化的表达式。 因此，我们首先必须使用运算顺序完全分别简化分子和分母。 然后我们将分子除以分母，因为分数条表示除法。

示例\(\PageIndex{22}\): How to Simplify Complex Fractions

简化：\(\dfrac{\left(\frac{1}{2}\right)^2}{4+3^2}\)。

回答

示例\(\PageIndex{23}\)

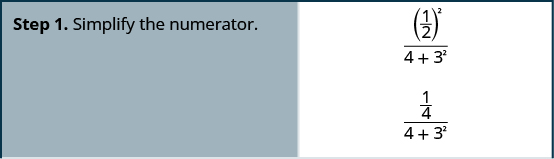
简化：\(\dfrac{\left(\frac{1}{3}\right)^2}{2^3+2}\)。

回答

\(\frac{1}{90}\)

示例\(\PageIndex{24}\)

简化：\(\dfrac{1+4^2}{\left(\frac{1}{4}\right)^2}\)。

回答

272

简化复杂分数。

1. 简化分子。
2. 简化分母。
3. 将分子除以分母。 尽可能简化。

示例\(\PageIndex{25}\)

简化：\(\dfrac{\dfrac{1}{2}+\dfrac{2}{3}}{\dfrac{3}{4}−\dfrac{1}{6}}\)。

回答

在分子和分母两边加上括号可能会有所帮助。

\(\begin{array}{lc}\text{} & \dfrac{\dfrac{1}{2}+\dfrac{2}{3}}{\dfrac{3}{4}−\dfrac{1}{6}} \\[6pt] \text{Simplify the numerator }(LCD=6)\text{ and } \\[6pt] \text{simplify the denominator }(LCD=12). & \dfrac{\left(\dfrac{3}{6}+\dfrac{4}{6}\right)}{\left(\dfrac{9}{12}−\dfrac{2}{12}\right)} \\[6pt] \text{Simplify.} & \left(\dfrac{7}{6}\right)\left(\dfrac{7}{12}\right) \\[6pt] \text{Divide the numerator by the denominator.} & \dfrac{7}{6}÷\dfrac{7}{12} \\[6pt] \text{Simplify.} & \dfrac{7}{6}⋅\dfrac{12}{7} \\[6pt] \text{Divide out common factors.} & \dfrac{\cancel{7}⋅\cancel{6}⋅2}{ \cancel{6}⋅\cancel{7}⋅1} \\[6pt] \text{Simplify.} & 2 \end{array}\)

示例\(\PageIndex{26}\)

简化：\( \dfrac{\dfrac{1}{3}+\dfrac{1}{2}}{ \dfrac{3}{4}−\dfrac{1}{3}}\)。

回答

2

示例\(\PageIndex{27}\)

简化：\(\dfrac{\dfrac{2}{3}−\dfrac{1}{2}}{ \dfrac{1}{4}+\dfrac{1}{3}}\)。

回答

\(\frac{2}{7}\)

使用分数计算变量表达式

我们以前计算过表达式，但现在我们可以用分数计算表达式了。 请记住，要计算表达式，我们要将变量的值替换为表达式，然后进行简化。

示例\(\PageIndex{28}\)

评估\(2x^2y\)何时\(x=\frac{1}{4}\)和\(y=−\frac{2}{3}\)。

回答

将值替换到表达式中。

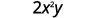
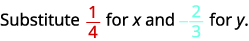
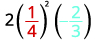
首先简化指数。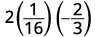
乘以；除去常见因子。 请注意，我们将 16 写成 2⋅2⋅42·2·4，以便于移除常见因素。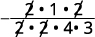
简化。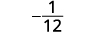

示例\(\PageIndex{29}\)

评估\(3ab^2\)何时\(a=−\frac{2}{3}\)和\(b=−\frac{1}{2}\)。

回答

\(−\dfrac{1}{2}\)

示例\(\PageIndex{30}\)

评估\(4c^3d\)何时\(c=−\frac{1}{2}\)和\(d=−\frac{4}{3}\)。

回答

\(\dfrac{2}{3}\)

访问此在线资源以获取更多指导和分数练习。

• 使用不同分母添加分数

关键概念

• 如果\(a\)\(b\)、和\(c\)是数字，其中\(b≠0,c≠0\)，那么

\(\dfrac{a}{b}=\dfrac{a·c}{b·c}\)和\(\dfrac{a·c}{b·c}=\dfrac{a}{b}.\)

• 如何简化分数。
  1. 重写分子和分母以显示常见因子。
     如果需要，先将分子和分母分数分成素数。
  2. 通过除去常见因子来简化等效分数属性的使用。
  3. 将所有剩余因子相乘。
• 如果\(a\)、\(b\)\(c\)、和\(d\)是数字，其中\(b≠0\)、和\(d≠0\)，那么

  \(\dfrac{a}{b}·\dfrac{c}{d}=\dfrac{ac}{bd}\)

  要乘以分数，请将分子相乘并乘以分母。

• 如果\(a\)\(b\)、\(c\)、和\(d\)是数字\(b≠0\)，其中\(c≠0\)、和\(d≠0\)，那么

  \(\dfrac{a}{b}÷\dfrac{c}{d}=\dfrac{a}{b}⋅\dfrac{d}{c}\)

  要除以分数，我们将第一个分数乘以第二个分数的倒数。

• 如果\(a\)\(b\)、和\(c\)是数字，其中\(c≠0\)，那么

  \(\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \text{ and } \dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\)

  要加上或减去分数，请将分子相加或减去，然后将结果置于公分母之上。

• 如何添加或减去分数。
  1. 他们有共同点吗？
     • 是-转到步骤 2。
     • 否-使用 LCD（最小公分母）重写每个分数。
       • 找到液晶屏。
       • 将每个分数更改为等效分数，以 LCD 为其分母。
  2. 加上或减去分数。
  3. 尽可能简化。
• 如何使用分数条简化表达式。
  1. 简化分子中的表达式。 简化分母中的表达式。
  2. 简化分数。
• 对于任何正数\(a\)\(b\)和

  \(\dfrac{−a}{b}=\dfrac{a}{−b}=−\dfrac{a}{b}\)

• 如何简化复杂分数。
  1. 简化分子。
  2. 简化分母。
  3. 将分子除以分母。 尽可能简化。

词汇表

复杂分数

分子或分母是分数的分数称为复数分数。

分母

用分数写成\(\dfrac{a}{b}\)，其中\(b≠0\)，分母\(b\)是整数被划分为的相等部分的数量。

等效分数

等效分数是具有相同值的分数。

分数

分数是写的\(\dfrac{a}{b}\)\(b≠0\)，其中，a 是分子，\(b\)是分母。 分数代表整体的各个部分。

最小公分母

两个分数的最小公分母 (LCD) 是其分母的最小公倍数 (LCM)。

分子

在分数中\(\dfrac{a}{b}\)，写在哪里\(b≠0\)，分子 a 表示包含了多少个部分。

倒数

分数的倒数是通过反转分数，将分子放在分母中，将分母放在分子中来得出的。