1.3: 整数
- Page ID
- 203928
在本节结束时,您将能够:
- 使用绝对值简化表达式
- 加上和减去整数
- 整数的乘法和除法
- 使用整数简化表达式
- 使用整数计算变量表达式
- 将短语翻译成带整数的表达式
- 在应用程序中使用整数
可以在基本代数章节 “基础” 中找到对本节所涵盖主题的更详尽的介绍。
使用绝对值简化表达式
负数是小于 0 的数字。 负数位于数字行零的左边(图\(\PageIndex{1}\))。
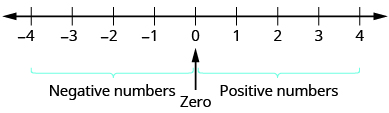
图\(\PageIndex{1}\)。 数字线显示正数和负数的位置。
你可能已经注意到,在数字行上,负数是正数的镜像,中间为零。 由于数字\(2\)和距离零\(−2\)的距离相同,因此每个数字和被称为相反的数字。 与\(2\) is 相反\(−2\),与\(−2\) is 相反\(2\)。
与数字相反的是数字线上与零的距离相同但与零相反的数字。
该@@ 图\(\PageIndex{2}\)说明了定义。

图\(\PageIndex{2}\)。 3 的反面是\(−3\)。
\[\begin{align} & -a \text{ means the opposite of the number }a \\ & \text{The notation} -a \text{ is read as “the opposite of }a \text{.”} \end{align} \]
我们看到诸如 3 和 −3 之类的数字是相反的,因为它们与数字线上的 0 的距离相同。 它们都是从 0 开始的三个单位。 0 与数字线上任何数字之间的距离称为该数字的绝对值。
数字的绝对值是它在数字线上距离 0 的距离。
数字\(n\)的绝对值以所有数字\(|n|\)\(|n|≥0\)的形式写入。
绝对值始终大于或等于零。
例如,
\[\begin{align} & -5 \text{ is } 5 \text{ units away from 0, so } |-5|=5. \\ & 5 \text{ is }5\text{ units away from 0, so }|5|=5. \end{align}\]
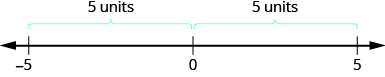
数字的绝对值永远不会为负数,因为距离不能为负。 绝对值等于零的唯一数字是数字零本身,因为数字线上从 0 到 0 的距离是零个单位。
在下一个示例中,我们将对具有绝对值的表达式进行排序。
\(=\)为以下每对数字填写\(<,\,>,\)或:
- \(\mathrm{|−5|}\_\_\mathrm{−|−5|}\_\_\mathrm{−|5|}\)
- \(\text{8__−|−8|}\)
- \(\text{−9__−|−9|}\)
- (\ text {− (−16) __|−16|}\)。
- 回答
-
一个。
\(\begin{array}{lrcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {|−5| \\ 5 \\ 5 \\ |−5|} & {\_\_ \\ \_\_ \\ > \\ >} & {−|−5| \\ −5 \\ −5 \\ −|−5|} \end{array}\)
b。
\(\begin{array}{llcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {8 \\ 8 \\ 8 \\ 8} & {\_\_ \\ \_\_ \\ > \\ >} & {−|−8| \\ −8 \\ −8 \\ −|−8|} \end{array}\)
c。
\(\begin{array}{lrcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {−9 \\ −9 \\ −9 \\ −9} & {\_\_ \\ \_\_ \\ = \\ =} & {−|−9| \\ −9 \\ −9 \\ −|−9|} \end{array}\)
d。
\(\begin{array}{lrcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {−(−16) \\ 16 \\ 16 \\ −(−16)} & {\_\_ \\ \_\_ \\ = \\ =} & {−|−16| \\ 16 \\ 16 \\ |−16|} \end{array}\)
\(=\)为以下每对数字填写\(<,\,>,\)或:
ⓐ\(−9 \_\_−|−9|\) ⓑ\(2 \_\_−|−2|\) ⓒ\(−8 \_\_|−8|\) ⓓ\(−(−9) \_\_|−9|.\)
- 回答
-
ⓐ\(>\) ⓑ\(>\) ⓒ\(<\)
ⓓ\(=\)
\(=\)为以下每对数字填写\(<,>,\)或:
- \(7 \_\_ −|−7|\)
- \(−(−10) \_ \_|−10|\)
- \(|−4| \_\_ −|−4|\)
- \(−1 \_\_ |−1|.\)
- 回答
-
ⓐ\(>\) ⓑ\(=\) ⓒ\(>\)
ⓓ\(<\)
现在,我们在分组符号列表中添加绝对值条。 当我们使用运算顺序时,首先我们尽可能简化绝对值柱的内部,然后取结果数字的绝对值。
\[\begin{array}{lclc} \text{Parentheses} & () & \text{Braces} & \{ \} \\ \text{Brackets} & [] & \text{Absolute value} & ||\end{array}\]
在下一个示例中,我们首先简化绝对值柱内的表达式,就像使用圆括号一样。
简化:\(\mathrm{24−|19−3(6−2)|}\)。
- 回答
-
\(\begin{array}{lc} \text{} & 24−|19−3(6−2)| \\ \text{Work inside parentheses first:} & \text{} \\ \text{subtract 2 from 6.} & 24−|19−3(4)| \\ \text{Multiply 3(4).} & 24−|19−12| \\ \text{Subtract inside the absolute value bars.} & 24−|7| \\ \text{Take the absolute value.} & 24−7 \\ \text{Subtract.} & 17 \end{array}\)
简化:\(19−|11−4(3−1)|\)。
- 回答
-
16
简化:\(9−|8−4(7−5)|\)。
- 回答
-
9
加减整数
到目前为止,在我们的示例中,我们只使用了计数数字和整数。
\[\begin{array}{ll} \text{Counting numbers} & 1,2,3… \\ \text{Whole numbers} 0,1,2,3…. \end{array}\]
我们使用对立面为我们提供了一种定义整数的方法。 整数及其对立面称为整数。 整数是数字\(…−3,−2,−1,0,1,2,3…\)
整数及其对立面称为整数。
整数是数字
\[…-3,-2,-1,0,1,2,3…,\]
大多数学生都对正数的加法和减法数值感到满意。 但是,同时使用正数和负数进行加法或减法可能更具挑战性。
我们将使用两个颜色计数器来模拟负数的加法和减法,这样你就可以直观地看到过程而不是记住规则。
我们让一种颜色(蓝色)代表正数。 另一种颜色(红色)将代表底片。

如果我们有一个正计数器和一个负计数器,则该对的值为零。 它们形成中性对。 这个中性货币对的价值为零。
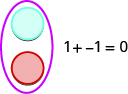
我们将使用计数器来显示如何添加:
\[5+3 \; \; \; \; \; \; −5+(−3) \; \; \; \; \; \; −5+3 \; \; \; \; \; \; \; 5+(−3)\]
第一个例子\(5+3,\)将 5 个正数和 3 个正数相加,均为正数。
第二个例子\(−5+(−3),\)将 5 个负数和 3 个负数相加,均为负数。
当标志相同时,计数器都是相同的颜色,因此我们添加它们。 在每种情况下,我们得到 8 个正面或 8 个负面。

那么,当迹象不同时会发生什么? 让我们添加\(−5+3\)和\(5+(−3)\)。
当我们使用计数器对正整数和负整数的加法进行建模时,很容易看出正数计数器还是更多负计数器。 因此,我们知道总和是正数还是负数。
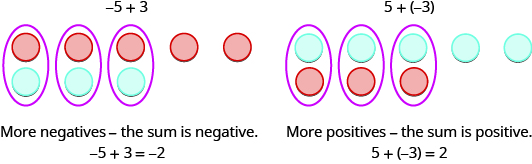
添加:ⓐ\(−1+(−4)\) ⓑ\(−1+5\) ⓒ\(1+(−5)\)。
- 回答
-
ⓐ
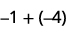

1 个负面加上 4 个负面是 5 个负面 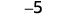
ⓑ
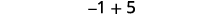

有更多的正数,所以总和是正数。 
ⓒ
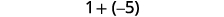

还有更多的负数,所以总和是负数。 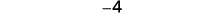
添加:ⓐ\(−2+(−4)\) ⓑ\(−2+4\) ⓒ\(2+(−4)\)。
- 回答
-
ⓐ\(−6\) ⓑ\(2\) ⓒ\(−2\)
添加:ⓐ\(−2+(−5)\) ⓑ\(−2+5\) ⓒ\(2+(−5)\)。
- 回答
-
ⓐ\(−7\) ⓑ\(3\) ⓒ\(−3\)
我们将继续使用计数器对减法进行建模。 也许当你年轻的时候,你会读\(“5−3”\)作 “5 take away 3”。 当你使用计数器时,你可以用同样的方式考虑减法!
我们将使用计数器来显示减去:
\[5−3 \; \; \; \; \; \; −5−(−3) \; \; \; \; \; \; −5−3 \; \; \; \; \; \; 5−(−3) \]
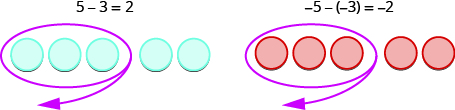
第一个例子是\(5−3\),我们从 5 个正数中减去 3 个正数,最后得到 2 个正数。
在第二个例子中,\(−5−(−3),\)我们从 5 个负数中减去 3 个负数,最后得到 2 个负数。
每个例子只使用一种颜色的计数器,而且 “外卖” 减法模型很容易应用。
当我们必须减去一个正数和一个负数时会发生什么? 我们需要同时使用蓝色和红色计数器以及一些中性对子。 如果我们没有带走所需的计数器数量,则添加中性对。 添加中性货币对不会改变该值。 这就像将季度改为镍一样——价值相同,但看起来不同。
让我们来看看\(−5−3\)和\(5−(−3)\)。
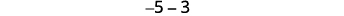 |
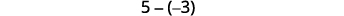 |
|
| 对第一个数字进行建模。 |  |
 |
| 我们现在添加所需的中性对。 |  |
 |
| 我们删除以第二个数字建模的计数器数量。 | 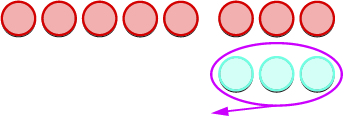 |
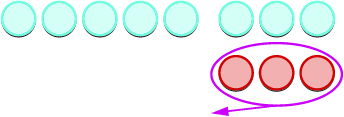 |
| 数一下还剩下什么。 |  |
 |
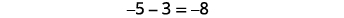 |
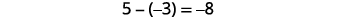 |
|
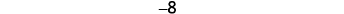 |
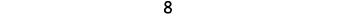 |
减去:ⓐ\(3−1\) ⓑ\(−3−(−1)\) ⓒ\(−3−1\) ⓓ\(3−(−1)\)。
- 回答
-
ⓐ
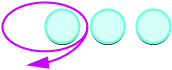
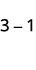
从 3 个阳性中取出 1 个阳性,得到 2 个阳性。 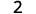
ⓑ

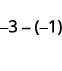
从 3 个阴性中取出 1 个阳性,得到 2 个阴性。 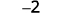
ⓒ

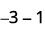
从添加的一对中性线中取出 1 个正数。 
ⓓ

从添加的一对中性线中取出 1 个负数。 

减去:ⓐ\(6−4\) ⓑ\(−6−(−4)\) ⓒ\(−6−4\) ⓓ\(6−(−4)\)。
- 回答
-
ⓐ\(2\) ⓑ\(−2\) ⓒ\(−10\) ⓓ\(10\)
减去:ⓐ\(7−4\) ⓑ\(−7−(−4)\) ⓒ\(−7−4\) ⓓ\(7−(−4)\)。
- 回答
-
ⓐ\(3\) ⓑ\(−3\) ⓒ\(−11\) ⓓ\(11\)
你有没有注意到有符号数字的减法可以通过相反的相加来完成? 在最后一个示例\(−3−1\)中,等\(3−(−1)\)于\(−3+(−1)\)和相同\(3+1\)。 你经常会看到这个概念,即减法属性,内容如下:
\[a−b=a+(−b)\]
减去一个数字等于将其相反的数字相加。
简化:ⓐ\(13−8\) 和\(13+(−8)\) ⓑ\(−17−9\) 和\(−17+(−9)\) ⓒ\(9−(−15)\) 和\(9+15\) ⓓ\(−7−(−4)\) 和\(−7+4\)。
- 回答
-
ⓐ
\(\begin{array}{lccc} \text{} & 13−8 & \text{and} & 13+(−8) \\ \text{Subtract.} & 5 & \text{} & 5 \end{array}\)ⓑ
\(\begin{array}{lccc} \text{} & −17−9 & \text{and} & −17+(−9) \\ \text{Subtract.} & −26 & \text{} & −26 \end{array}\)
ⓒ
\(\begin{array}{lccc} \text{} & 9−(−15) & \text{and} & 9+15 \\ \text{Subtract.} & 24 & \text{} & 24 \end{array}\)
ⓓ
\(\begin{array}{lccc} \text{} & −7−(−4) & \text{and} & −7+4 \\ \text{Subtract.} & −3 & \text{} & −3 \end{array}\)
简化:ⓐ\(21−13\) 和\(21+(−13)\) ⓑ\(−11−7\) 和\(−11+(−7)\) ⓒ\(6−(−13)\) 和\(6+13\) ⓓ\(−5−(−1)\) 和\(−5+1\)。
- 回答
-
ⓐ\(8,8\) ⓑ\(−18,−18\)
ⓒ\(19,19\) ⓓ\(−4,−4\)
简化:ⓐ\(15−7\) 和\(15+(−7)\) ⓑ\(−14−8\) 和\(−14+(−8)\) ⓒ\(4−(−19)\) 和\(4+19\) ⓓ\(−4−(−7)\) 和\(−4+7\)。
- 回答
-
ⓐ\(8,8\) ⓑ\(−22,−22\)
ⓒ\(23,23\) ⓓ\(3,3\)
当整数超过三个时会发生什么? 我们照常使用操作顺序。
简化:\(7−(−4−3)−9.\)
- 回答
-
\(\begin{array}{lc} \text{} & 7−(−4−3)−9 \\ \text{Simplify inside the parentheses first.} & 7−(−7)−9 \\ \text{Subtract left to right.} & 14−9 \\ \text{Subtract.} & 5 \end{array}\)
简化:\(8−(−3−1)−9.\)
- 回答
-
3
简化:\(12−(−9−6)−14.\)
- 回答
-
13
乘以和除以整数
由于乘法是重复加法的数学简写,因此我们的模型可以很容易地应用于显示整数的乘法。 让我们来看看这个具体的模型,看看我们注意到了什么模式。 我们将使用与加法和减法相同的示例。 在这里,我们使用模型只是为了帮助我们发现模式。
我们记得 a⋅ba·b 的意思是加 a, b 倍。
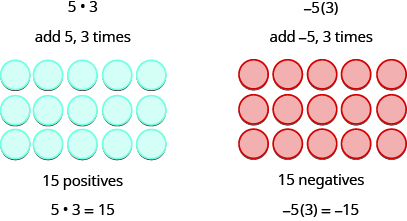
接下来的两个例子更有趣。 将 5 乘以 −3 是什么意思? 这意味着减去 5,3 倍。 将减法视为 “带走”,这意味着扣除5、3次。 但是没有什么可带走的,所以我们首先在工作空间中添加中性对。
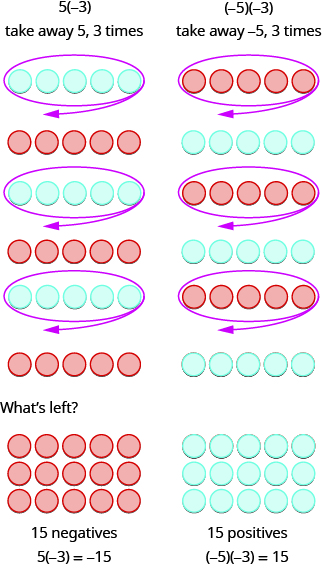
总而言之:
\[\begin{array}{ll} 5·3=15 & −5(3)=−15 \\ 5(−3)=−15 & (−5)(−3)=15 \end{array}\]
请注意,要将两个有符号数字相乘,当
\[ \text{signs are the } \textbf{same} \text{, the product is } \textbf{positive.} \\ \text{signs are } \textbf{different} \text{, the product is } \textbf{negative.} \]
那分裂呢? 除法是乘法的逆运算。 所以,\(15÷3=5\)因为\(15·3=15\)。 换句话说,这个表达式说15可以分成3组,每组5个,因为将五加三次得出15。 如果你看一些整数相乘的例子,你可能会想出整数除以的规则。
\[\begin{array}{lclrccl} 5·3=15 & \text{so} & 15÷3=5 & \text{ } −5(3)=−15 & \text{so} & −15÷3=−5 \\ (−5)(−3)=15 & \text{so} & 15÷(−3)=−5 & \text{ } 5(−3)=−15 & \text{so} & −15÷(−3)=5 \end{array}\]
在符号方面,除法遵循与乘法相同的规则。
用于两个有符号数字的乘法和除法:
| 同样的迹象 | 结果 |
|---|---|
| • 两个积极因素 | 阳性 |
| • 两张底片 | 阳性 |
如果信号相同,则结果为阳性。
| 不同的迹象 | 结果 |
|---|---|
| • 正面和负面 | 负面的 |
| • 负面和阳性 | 负面的 |
如果符号不同,则结果为负数。
乘以或除以:ⓐ\(−100÷(−4)\) ⓑ\(7⋅6\) ⓒ\(4(−8)\) ⓓ\(−27÷3.\)
- 回答
-
ⓐ
\(\begin{array}{lc} \text{} & −100÷(−4) \\ \text{Divide, with signs that are} \\ \text{the same the quotient is positive.} & 25 \end{array}\)
ⓑ
\(\begin{array} {lc} \text{} & 7·6 \\ \text{Multiply, with same signs.} & 42 \end{array}\)
ⓒ
\(\begin{array} {lc} \text{} & 4(−8) \\ \text{Multiply, with different signs.} & −32 \end{array}\)
ⓓ
\(\begin{array}{lc} \text{} & −27÷3 \\ \text{Divide, with different signs,} \\ \text{the quotient is negative.} & −9 \end{array}\)
乘以或除以:ⓐ\(−115÷(−5)\) ⓑ\(5⋅12\) ⓒ\(9(−7)\) ⓓ\(−63÷7.\)
- 回答
-
ⓐ 23 ⓑ 60 ⓒ −63 ⓓ −9
乘以或除以:ⓐ\(−117÷(−3)\) ⓑ\(3⋅13\) ⓒ\(7(−4)\) ⓓ\(−42÷6\)。
- 回答
-
ⓐ 39 ⓑ 39 ⓒ −28 ⓓ −7
当我们将一个数字乘以 1 时,结果是相同的数字。 每当我们将一个数字乘以 −1 时,我们就会得到相反的数字!
\[−1a=−a\]
将数字乘以得\(−1\)出相反的结果。
使用整数简化表达式
当表达式中有两个以上的数字时会发生什么? 当包含负数时,运算顺序仍然适用。 记得请原谅我亲爱的莎莉阿姨吗?
让我们试试一些例子。 我们将简化使用所有四个整数运算(加法、减法、乘法和除法)的表达式。 记住要遵循操作顺序。
简化:ⓐ\((−2)^4\) ⓑ\(−2^4\)。
- 回答
-
注意 (a) 和 (b) 部分的区别。 在 (a) 部分中,指数表示将括号中的内容,即 −2 提高到第 4 次方。 在 (b) 部分中,指数意味着只将 2 提高到第 4 次方,然后取相反的次方。
ⓐ
\(\begin{array}{lc} \text{} & (−2)^4 \\ \text{Write in expanded form.} & (−2)(−2)(−2)(−2) \\ \text{Multiply.} & 4(−2)(−2) \\ \text{Multiply.} & −8(−2) \\ \text{Multiply.} & 16 \end{array}\)ⓑ
\(\begin{array}{lc} \text{} & −2^4 \\ \text{Write in expanded form.} & −(2·2·2·2) \\ \text{We are asked to find} & \text{} \\ \text{the opposite of }24. & \text{} \\ \text{Multiply.} & −(4·2·2) \\ \text{Multiply.} & −(8·2) \\ \text{Multiply.} & −16 \end{array}\)
简化:ⓐ\((−3)^4\) ⓑ\(−3^4\)。
- 回答
-
ⓐ 81 ⓑ −81
简化:ⓐ\((−7)^2\) ⓑ\(−7^2\)。
- 回答
-
ⓐ 49 ⓑ −49
最后一个例子向我们展示了\((−2)^4\)和之间的区别\(−2^4\)。 这种区别对于防止将来出现错误很重要。 下一个例子提醒我们按从左到右的顺序进行乘法和除法。
简化:ⓐ\(8(−9)÷(−2)^3\) ⓑ\(−30÷2+(−3)(−7)\)。
- 回答
-
ⓐ
\(\begin{array}{lc} \text{} & 8(−9)÷(−2)^3 \\ \text{Exponents first.} & 8(−9)÷(−8) \\ \text{Multiply.} & −72÷(−8) \\ \text{Divide.} & 9 \end{array}\)
ⓑ
\(\begin{array}{lc} \text{} & −30÷2+(−3)(−7) \\ \text{Multiply and divide} \\ \text{left to right, so divide first.} & −15+(−3)(−7) \\ \text{Multiply.} & −15+21 \\ \text{Add.} & 6 \end{array}\)
简化:ⓐ\(12(−9)÷(−3)^3\) ⓑ\(−27÷3+(−5)(−6).\)
- 回答
-
ⓐ 4 ⓑ 21
简化:ⓐ\(18(−4)÷(−2)^3\) ⓑ\(−32÷4+(−2)(−7).\)
- 回答
-
ⓐ 9 ⓑ 6
使用整数计算变量表达式
请记住,计算表达式意味着用数字代替表达式中的变量。 现在我们可以使用负数和正数。
评估\(4x^2−2xy+3y^2\)时间\(x=2,y=−1\)。
- 回答
-
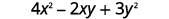
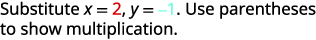
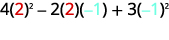
简化指数。 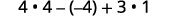
乘以。 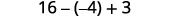
减去。 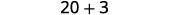
添加。 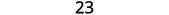
评估:\(3x^2−2xy+6y^2\)何时\(x=1,y=−2\)。
- 回答
-
31
评估:\(4x^2−xy+5y^2\)何时\(x=−2,y=3\)。
- 回答
-
67
将短语翻译成带整数的表达式
我们之前将英语翻译成代数的工作也适用于包含正数和负数的短语。
翻译和简化:8 和 −12 的总和增加 3。
- 回答
-
\(\begin{array}{lc} \text{} & \text{the } \textbf{sum } \underline{\text{of}} \; –8 \; \underline{\text{and}} −12 \text{ increased by } 3 \\ \text{Translate.} & [8+(−12)]+3 \\ \text{Simplify. Be careful not to confuse the} \; \; \; \; \; \; \; \; \; \; & (−4)+3 \\ \text{brackets with an absolute value sign.} \\ \text{Add.} & −1 \end{array}\)
翻译并简化 9 和 −16,增加 4。
- 回答
-
\((9+(−16))+4;−3\)
翻译并简化 −8 和 −12 的总和,增加 7。
- 回答
-
\((−8+(−12))+7;−13\)
在应用程序中使用整数
我们将概述解决应用程序的计划。 如果我们不知道自己在寻找什么或者该怎么称呼它,就很难找到东西! 因此,当我们解决应用程序时,我们首先需要确定问题要求我们找到什么。 然后我们将写一个短语来提供找到它的信息。 我们将把这个短语翻译成一个表达式,然后简化这个表达式以得到答案。 最后,我们用一句话总结答案,以确保答案合理。
一天早晨,印第安纳州肯德尔维尔的温度为11度。 到下午中旬,温度已降至−9−9度。 早上和下午的温度有什么区别?
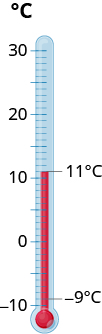
- 回答
-






一天早晨,阿拉斯加安克雷奇的温度为15度。 到下午中旬,温度已降至零下30度。 早上和下午的温度有什么区别?
- 回答
-
温度差为 45 华氏度。
午餐时间丹佛的温度为零下6度。 到了日落时分,温度已降至−15度。 午餐时间和日落温度有什么区别?
- 回答
-
温度差为9度。
- 阅读问题。 确保所有文字和想法都被理解。
- 确定我们被要求查找的内容。
- 写一个短语,提供找到它的信息。
- 将短语@@ 翻译成表达式。
- 简化表达式。
- 用完整的句子@@ 回答问题。
访问此在线资源以获取更多指导和整数练习。
- 用计数器减去整数
关键概念
- \[\begin{align} & −a \text{ means the opposite of the number }a \\ & \text{The notation} −a \text{ is read as “the opposite of }a \text{.”} \end{align} \]
- 数字的绝对值是它在数字线上距离 0 的距离。
数字 n 的绝对值写成所有数字\(|n|\)的\(|n|≥0\) and。
绝对值始终大于或等于零。
- \[\begin{array}{lclc} \text{Parentheses} & () & \text{Braces} & \{ \} \\ \text{Brackets} & [] & \text{Absolute value} & ||\end{array}\]
- 减法属性
\(a−b=a+(−b)\)
减去一个数字等于将其相反的值相加。 - 用于两个有符号数字的乘法和除法:
如果信号相同,则结果为阳性。同样的迹象 结果 • 两个积极因素 阳性 • 两张底片 阳性
如果符号不同,则结果为负数。不同的迹象 结果 • 正面和负面 负面的 • 负面和阳性 负面的 - 乘以\(−1\)
\(−1a=−a\)
将数字乘以得\(−1\)出相反的结果。
- 如何在应用程序中使用整数。
- 阅读问题。 确保所有文字和想法都被理解
- 确定我们被要求查找的内容。
- 写一个短语,提供找到它的信息。
- 将短语@@ 翻译成表达式。
- 简化表达式。
- 用完整的句子@@ 回答问题。
词汇表
- 绝对值
- 数字的绝对值是它与数字线\(0\)上的距离。
- 整数
- 整数及其对立面称为整数。
- 负数
- 小于\(0\)的数字是负数。
- 相反的
- 与数字相反的是数字线上与零的距离相同但与零相反的数字。


