9.3: الأطياف الجزيئية
- Page ID
- 196464
في نهاية هذا القسم، ستكون قادرًا على:
- استخدم مفاهيم الطاقة الاهتزازية والدورانية لوصف انتقالات الطاقة في جزيء ثنائي الذرة
- شرح السمات الرئيسية لطيف الطاقة الدورانية الاهتزازية لجزيء ثنائي الذرة
- تقدير الطاقات المسموح بها لجزيء دوار
- حدد مسافة فصل التوازن بين الذرات في جزيء ثنائي الذرة من طيف الامتصاص الدوراني الاهتزازي
تعد مستويات الطاقة الجزيئية أكثر تعقيدًا من مستويات الطاقة الذرية لأن الجزيئات يمكن أن تهتز وتدور أيضًا. تكمن الطاقات المرتبطة بهذه الحركات في نطاقات مختلفة وبالتالي يمكن دراستها بشكل منفصل. تكون التحولات الإلكترونية من الدرجة 1 eV، والتحولات الاهتزازية مرتبة\(10^{-2}eV\)، والتحولات الدورانية مرتبة\(10^{-3}eV\). بالنسبة للجزيئات المعقدة، يصعب توصيف هذه التغيرات في الطاقة، لذلك نبدأ بالحالة البسيطة للجزيء ثنائي الذرة.
الدوران الكمومي
وفقًا للميكانيكا الكلاسيكية، يتم إعطاء طاقة دوران الجزيء ثنائي الذرة بواسطة
\[E_r = \dfrac{L^2}{2I}, \nonumber \]
حيث I هي لحظة القصور الذاتي و L هي الزخم الزاوي. وفقًا لميكانيكا الكم، يتم قياس الزخم الزاوي الدوراني:
\[L = \sqrt{l(l + 1)} \hbar (l = 0,1,2,3,...), \nonumber \]
حيث l هو الرقم الكمي الزاوي المداري. وبالتالي فإن مستوى الطاقة الدورانية المسموح به لجزيء ثنائي الذرة هو
\[E_r = l(l + 1) \dfrac{\hbar^2}{2I} = l(l + 1) \, E_{0r} \, \, (l = 0,1,2,3,...), \nonumber \]
حيث يتم تعريف الطاقة الدورانية المميزة للجزيء على أنها
\[E_{0r} = \dfrac{\hbar^2}{2I}. \nonumber \]
بالنسبة للجزيء ثنائي الذرة، فإن لحظة القصور الذاتي مع الكتلة المنخفضة\(μ\) هي
\[I = \mu r_0^2, \nonumber \]
\(r_0\)أين المسافة الإجمالية بين الذرات. وبالتالي فإن فرق الطاقة بين مستويات الدوران هو
\[\Delta E_r = E_{l+1} - E_l = 2(l + 1) \, E_{0r}. \nonumber \]
تتطلب الدراسة التفصيلية للتحولات بين مستويات الطاقة الدورانية الناتجة عن امتصاص الإشعاع أو انبعاثه (ما يسمى بالانتقال الكهربائي ثنائي القطب) ما يلي:
\[\Delta l = \pm1. \label{delta l} \]
تحدد هذه القاعدة، المعروفة باسم قاعدة التحديد، التحولات المحتملة من حالة كمية إلى أخرى. المعادلة\ ref {delta l} هي قاعدة التحديد لتحولات الطاقة الدورانية. ينطبق فقط على الجزيئات ثنائية الذرة التي لها لحظة ثنائية القطب الكهربائية. لهذا السبب،\(N_2\) لا تتعرض الجزيئات المتماثلة مثل\(H_2\) وتحولات الطاقة الدورانية بسبب امتصاص أو انبعاث الإشعاع الكهرومغناطيسي.
حدِّد أدنى ثلاثة مستويات للطاقة الدورانية لجزيء كلوريد الهيدروجين ((\(\ce{HCl}\))).
إستراتيجية
كلوريد الهيدروجين (\(\ce{HCl}\)) هو جزيء ثنائي الذرة بمسافة فصل توازن قدرها 0.127 نانومتر. تعتمد مستويات الطاقة الدورانية فقط على زخم القصور الذاتي I والرقم الكمي للزخم الزاوي المداري\(l\) (في هذه الحالة\(l = 0\)، 1، و 2). يعتمد زخم القصور الذاتي بدوره على مسافة فصل التوازن (المعطاة) والكتلة المخفضة التي تعتمد على كتل ذرات H و Cl.
الحل
أولاً، نحسب الكتلة المخفضة. إذا كان الجسيم 1 هو الهيدروجين والجسيم 2 هو الكلوريد، فلدينا
\[\begin{align*} \mu &= \dfrac{m_1m_2}{m_1 + m_2} = \dfrac{(1.0 \, u)(35.4 \, u)}{1.0 \, u + 35.4 \, u} \\[4pt] &= 0.97 \, u = 0.97 \, u \left(\dfrac{931.5 \dfrac{MeV}{c^2}}{1 \, u}\right) \\[4pt] &= 906 \dfrac{MeV}{c^2}. \end{align*} \nonumber \]
وبالتالي فإن طاقة كتلة الراحة المقابلة هي
\[\mu c^2 = 9.06 \times 10^8 \, eV \nonumber \]
هذا يسمح لنا بحساب الطاقة المميزة:
\[ \begin{align*} E_{0r} &= \dfrac{\hbar^2}{2(\mu r_0^2)} = \dfrac{(\hbar c)^2}{2(\mu c^2)r_0^2} \nonumber \\[4pt] &= \dfrac{(197.3 \, eV \cdot nm)^2}{2(9.06 \times 10^8 eV)(0.127 \, nm)^2} \nonumber \\[4pt] &= 1.33 \times 10^{-3} eV. \nonumber \end{align*} \nonumber \]
(لاحظ كيف تتم كتابة هذا التعبير بدلالة طاقة الكتلة الباقية. هذه التقنية شائعة في حسابات الفيزياء الحديثة.) يتم تحديد مستويات الطاقة الدورانية بواسطة
\[E_r = l(l + 1) \dfrac{\hbar^2}{2I} = l(l + 1) E_{0r}, \nonumber \]
أين\(l\) هو الرقم الكمي المداري. وبالتالي فإن أدنى ثلاثة مستويات للطاقة الدورانية لجزيء HCl هي
\[\begin{align*} l &= 0:\quad E_r &&= 0 \, eV \, \text{(no rotation)} \\[4pt] l &= 1: \quad E_r &&= 2 \, E_{0r} = 2.66 \times 10^{-3}eV, \\[4pt] l &= 2:\quad E_r &&= 6 \, E_{0r} = 7.99 \times 10^{-3} eV. \end{align*} \nonumber \]
الدلالة
يرتبط الطيف الدوراني بانتقالات ضعيفة (1/1000 إلى 1/100 من eV). وبالمقارنة، فإن طاقة الإلكترون في الحالة الأرضية للهيدروجين هي\(- 13.6 \, eV\).
بماذا يخبرك فصل الطاقة بين خطوط الامتصاص في الطيف الدوراني لجزيء ثنائي الذرة؟
- إجابة
-
لحظة القصور الذاتي
الاهتزاز الكمومي
يصعب تقدير مستوى الطاقة الاهتزازية، وهو مستوى الطاقة المرتبط بالطاقة الاهتزازية للجزيء، مقارنة بمستوى الطاقة الدورانية. ومع ذلك، يمكننا تقدير هذه المستويات بافتراض أن الذرتين في الجزيء ثنائي الذرة مرتبطتان بنابض مثالي من ثابت الزنبرك k. الطاقة الكامنة لنظام الربيع هذا هي
\[U_{osc} = \dfrac{1}{2}k \Delta r^2, \nonumber \]
\(\Delta r\)أين يحدث تغيير في «الطول الطبيعي» للجزيء على طول الخط الذي يربط الذرات. يعطي حل معادلة شرودنغر لهذه الإمكانية
\[E_n = \left(n + \dfrac{1}{2}\right) \hbar \omega \, (n = 0,1,2,. . .), \nonumber \]
\(\omega\)أين التردد الزاوي الطبيعي للاهتزاز و n هو الرقم الكمي الاهتزازي. تبين أن التنبؤ بأن مستويات الطاقة الاهتزازية متباعدة بالتساوي (\(\Delta E = \hbar \omega\)) جيد في الطاقات المنخفضة.
تتطلب الدراسة التفصيلية للتحولات بين مستويات الطاقة الاهتزازية الناتجة عن امتصاص الإشعاع أو انبعاثه (وما يسمى على وجه التحديد بانتقال ثنائي القطب الكهربائي) ما يلي:
\[\Delta n = \pm 1. \label{delta n} \]
تمثل المعادلة\ ref {delta n} قاعدة التحديد لتحولات الطاقة الاهتزازية. كما ذكرنا سابقًا، تنطبق هذه القاعدة فقط على الجزيئات ثنائية الذرة التي لها لحظة ثنائية القطب الكهربائية. لا تواجه الجزيئات المتماثلة مثل هذه التحولات.
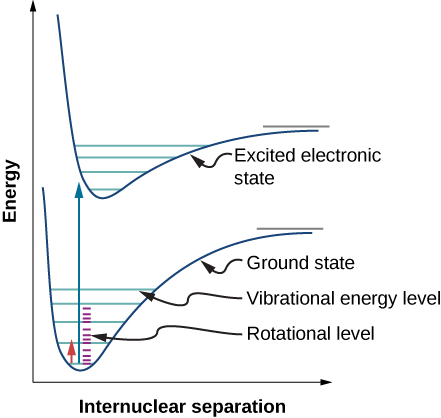
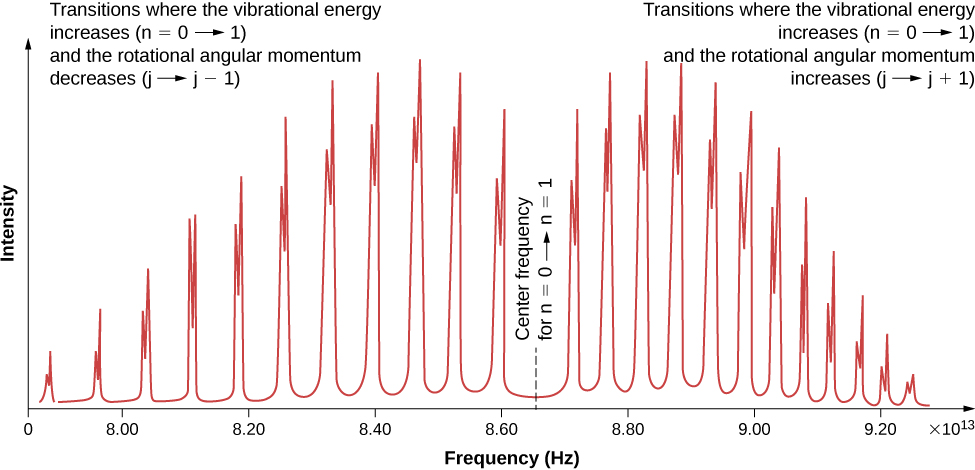
نظرًا لقواعد الاختيار، فإن امتصاص أو انبعاث الإشعاع بواسطة جزيء ثنائي الذرة ينطوي على انتقال في حالات الاهتزاز والدوران. على وجه التحديد، إذا تغير الرقم الكمي الاهتزازي (n) بوحدة واحدة، فإن الرقم الكمي الدوراني (l) يتغير بوحدة واحدة. يوضح الشكل رسم تخطيطي لمستوى الطاقة للانتقال المحتمل\(\PageIndex{1}\). يظهر طيف الامتصاص لمثل هذه التحولات في كلوريد الهيدروجين (HCl) في الشكل (\ pageIndex {2}\). تعود قمم الامتصاص إلى التحولات من الحالات\(n = 1\) الاهتزازية\(n = 0\) إلى الحالة الاهتزازية. اختلافات الطاقة لنطاق القمم على اليسار واليمين هي، على التوالي:
(الفرقة اليمنى)
\[ \Delta E_{l \rightarrow l+1} = \hbar \omega + 2(l + 1)E_{0r} = \hbar \omega + 2E_{0r}, \, \hbar \omega + 4E_{0r}, \, \hbar \omega + 6E_{0r}, ... \nonumber \]
(الفرقة اليسرى)
\[ \Delta E_{l \rightarrow l-1} = \hbar \omega - 2l E_{0r} = \hbar \omega - 2E_{0r}, \, \hbar \omega - 4E_{0r}, \, \hbar \omega - 6E_{0r}, .... \nonumber \]
يمكن بعد ذلك تحديد لحظة القصور الذاتي من تباعد الطاقة بين القمم الفردية (\(2E_{0r}\)) أو من الفجوة بين النطاقين الأيسر والأيمن (\(4E_{0r}\)). التردد في مركز هذه الفجوة هو تردد الاهتزاز.