7.A: ميكانيكا الكم (الإجابات)

Last updated
Save as PDF

Page ID: 196775

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

تحقق من فهمك

7.1. \(\displaystyle (3+4i)(3−4i)=9−16i^2=25\)

7.2. \(\displaystyle A=\sqrt{2/L}\)

7.3. \(\displaystyle (1/2−1/π)/2=9%\)

7.4. \(\displaystyle 4.1×10^{−8}eV; 1.1×10^{−5}nm\)

7.5. \(\displaystyle 0.5mω^2x^2ψ(x)∗ψ(x)\)

7.6. لا شيء. تحتوي الوظيفة الأولى على انقطاع؛ والوظيفة الثانية ذات قيمة مزدوجة؛ وتتباعد الوظيفة الثالثة بحيث لا يمكن تطبيعها.

7.7. أ. 9.1 في المائة؛

ب. 25%

7.8. أ. 295 نيوتن/متر؛

ب. 0.277 فولت

7.9. \(\displaystyle ⟨x⟩=0\)

7.10. \(\displaystyle L_{proton}/L_{electron}=\sqrt{m_e/m_p}=2.3%\)

أسئلة مفاهيمية

1. \(\displaystyle 1/\sqrt{L}\)، أين\(\displaystyle L=length\)؛ 1/L، أين\(\displaystyle L=length\)

3. لا تتوافق وظيفة الموجة بشكل مباشر مع أي كمية مقاسة. إنها أداة للتنبؤ بقيم الكميات الفيزيائية.

5. متوسط قيمة الكمية الفيزيائية لعدد كبير من الجسيمات التي لها نفس وظيفة الموجة.

7. نعم، إذا كان موقعها غير معروف تمامًا. نعم، إذا كان زخمها غير معروف تمامًا.

9. لا. وفقًا لمبدأ عدم اليقين، إذا كان عدم اليقين بشأن موضع الجسيم صغيرًا، يكون عدم اليقين بشأن زخمه كبيرًا. وبالمثل، إذا كان عدم اليقين بشأن موضع الجسيم كبيرًا، فإن عدم اليقين بشأن زخمه يكون صغيرًا.

11. لا، هذا يعني أن التنبؤات حول الجسيم (المعبر عنها من حيث الاحتمالات) مستقلة عن الوقت.

13. لا، لأن احتمال وجود الجسيم في فترة ضيقة (صغيرة للغاية) عند الانقطاع غير محدد.

15. لا. بالنسبة للبئر المربع اللانهائي، يزداد التباعد بين مستويات الطاقة مع زيادة العدد الكمي n. تتوافق أصغر طاقة تم قياسها مع الانتقال من n = 2 إلى 1، وهو ثلاثة أضعاف طاقة الحالة الأرضية. تتوافق أكبر طاقة تم قياسها مع الانتقال من\(\displaystyle n=∞\) إلى 1، وهو اللانهاية. (ملاحظة: حتى الجسيمات ذات الطاقات الكبيرة للغاية تظل مرتبطة ببئر مربع لا نهائي - لا يمكنها أبدًا «الهروب»)

17. لا. تتوافق هذه الطاقة مع\(\displaystyle n=0.25\)، ولكن يجب أن تكون n عددًا صحيحًا.

19. لأن أصغر قيمة مسموح بها للرقم الكمي n لمذبذب توافقي بسيط هي 0. لا، لأن ميكانيكا الكم والميكانيكا الكلاسيكية تتفق فقط في حدود nn الكبيرة.

21. نعم، ضمن قيود مبدأ عدم اليقين. إذا كان الجسيم المتذبذب موضعيًا، يتم توزيع الزخم وبالتالي طاقة المذبذب.

23. مضاعفة عرض الحاجز

25. لا، قوة الاستعادة على الجسيم عند جدران بئر مربع غير محدود هي اللانهاية.

مشاكل

27. \(\displaystyle ∣ψ(x)∣^2sin^2ωt\)

29. (أ) و (ه) يمكن تطبيعهما

31. أ\(\displaystyle A=\sqrt{2α/π}\)؛

ب\(\displaystyle probability=29.3%\)؛

ج\(\displaystyle ⟨x⟩=0⟨x⟩=0\).

د\(\displaystyle ⟨p⟩=0\)؛

ه.\(\displaystyle ⟨K⟩=α^2ℏ^2/2m\)

33. أ\(\displaystyle Δp≥2.11×10^{−34}N⋅s\)؛

ب\(\displaystyle Δv≥6.31×10^{−8}m\)؛

ج.\(\displaystyle Δv/\sqrt{k_BT/m_α}=5.94×10^{−11}\)

35. \(\displaystyle Δτ≥1.6×10^{−25}s\)

37. أ\(\displaystyle Δf≥1.59MHz\)؛

ب.\(\displaystyle Δω/ω_0=3.135×10^{−9}\)

39. تنفيذ عوائد المشتقات\(\displaystyle k^2=\frac{ω^2}{c^2}\).

41. يؤدي تنفيذ المشتقات (كما هو موضح أعلاه) للدالة الجيبية إلى إعطاء جيب التمام على الجانب الأيمن المعادلة، وبالتالي تفشل المساواة. يحدث نفس الشيء بالنسبة لمحلول جيب التمام.

43. \(\displaystyle E=ℏ^2k^2/2m\)

45. \(\displaystyle ℏ^2k^2ℏ\)؛ للجسيم زخم محدد وبالتالي يتعادل الزخم المحدد.

47. 9.4 فولت، 64٪

49. 0.38 نانومتر

51. 1.82 ميللي فولت

53. 24.7 نانومتر

55. \(\displaystyle 6.03Å\)

57. أ.

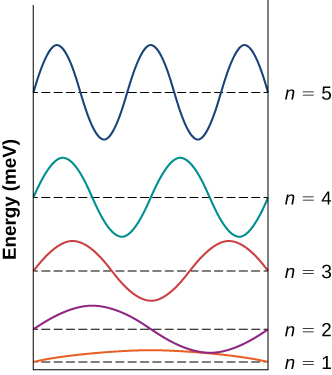
يتم عرض وظائف الموجة للحالات من n =1 إلى n = 5 للإلكترون في بئر مربع غير محدود. يتم إزاحة كل دالة رأسيًا بواسطة طاقتها، ويتم قياسها بm e V. حالة n=1 هي الموجة النصفية الأولى للدالة الجيبية. الدالة n=2 هي الموجة الكاملة الأولى للدالة الجيبية. الدالة n=3 هي أول موجة ونصف من الدالة الجيبية. الدالة n=4 هي أول موجتين من الدالة الجيبية. الدالة n=5 هي أول موجتين ونصف من الدالة الجيبية.

يتم عرض وظائف الموجة للحالات من n =1 إلى n = 5 للإلكترون في بئر مربع غير محدود. يتم إزاحة كل دالة رأسيًا عن طريق طاقتها، ويتم قياسها بالمي فولت. الحالة n=1 هي الموجة النصفية الأولى للدالة الجيبية. الدالة n=2 هي الموجة الكاملة الأولى للدالة الجيبية. الدالة n=3 هي أول موجة ونصف من الدالة الجيبية. الدالة n=4 هي أول موجتين من الدالة الجيبية. الدالة n=5 هي أول موجتين ونصف من الدالة الجيبية. ؛

ب.\(\displaystyle λ_{5→3}=12.9nm,λ_{3→1}=25.8nm,λ_{4→3}=29.4nm\)

59. برهان

61. \(\displaystyle 6.662×10^{14}Hz\)

63. \(\displaystyle n≈2.037×10^{30}\)

65. \(\displaystyle ⟨x⟩=0.5mω^2⟨x^2⟩=ℏω/4\)؛\(\displaystyle ⟨K⟩=⟨E⟩−⟨U⟩=ℏω/4\)

67. برهان

69. تفي دالة معقدة من الشكل،\(\displaystyle Ae^{iϕ}\)، بمعادلة Schrdinger المستقلة عن الوقت. تكون عوامل التشغيل الخاصة بالطاقة الحركية والطاقة الكلية خطية، لذا فإن أي مزيج خطي من هذه الوظائف الموجية يعد أيضًا حلاً صالحًا لمعادلة Schrdinger. لذلك، نستنتج أن المعادلة 7.68 تفي بالمعادلة 7.61، والمعادلة 7.69 تفي بالمعادلة 7.63.

71. أ. 4.21%؛

(ب) 0.84 في المائة؛

ج. 0.06%

73. أ. 0.13%؛

ب. ما يقرب من 0٪

75. 0.38 نانومتر

مشاكل إضافية

77. برهان

79. أ. 4.0 في المائة؛

(ب) 1.4 في المائة؛

(ج) 4.0%;

د. 1.4%

81. أ\(\displaystyle t=mL^2/h=2.15×10^{26}years\)؛

ب.\(\displaystyle E_1=1.46×10^{−66}J,K=0.4J\)

83. برهان

85. 1.2 نيوتن/متر

87. 0

مشاكل التحدي

89. 19.2 ميكرومتر؛ 11.5 ميكرومتر مكعب؛ 11.5 ميكرومتر

91. 3.92%

93. برهان