7.7: النفق الكمي للجسيمات من خلال الحواجز المحتملة
- Page ID
- 196772
في نهاية هذا القسم، ستكون قادرًا على:
- وصف كيف يمكن لجسيم كمي أن يمر عبر حاجز محتمل
- حدد المعلمات الفيزيائية المهمة التي تؤثر على احتمالية حفر الأنفاق
- حدد الظواهر الفيزيائية التي يتم فيها ملاحظة الأنفاق الكمومية
- شرح كيفية استخدام الأنفاق الكمومية في التقنيات الحديثة
النفق الكمومي هو ظاهرة تخترق فيها الجسيمات حاجز طاقة محتمل بارتفاع أكبر من الطاقة الكلية للجسيمات. هذه الظاهرة مثيرة للاهتمام ومهمة لأنها تنتهك مبادئ الميكانيكا الكلاسيكية. يعد حفر الأنفاق الكمومية أمرًا مهمًا في نماذج الشمس وله مجموعة واسعة من التطبيقات، مثل مجهر المسح النفقي والصمام الثنائي النفقي.
حفر الأنفاق والطاقة الكامنة
لتوضيح النفق الكمومي، ضع في اعتبارك كرة تتدحرج على سطح بطاقة حركتها 100 J. عندما تتدحرج الكرة، تصطدم بتل. تبلغ الطاقة الكامنة للكرة الموضوعة فوق التل 10 جول، لذلك تتدحرج الكرة (بقوة 100 جول من الطاقة الحركية) بسهولة فوق التل وتستمر في التقدم. في الميكانيكا الكلاسيكية، احتمال مرور الكرة فوق التل هو بالضبط 1 - إنها تصل إلى النهاية في كل مرة. ومع ذلك، إذا زاد ارتفاع التل - كرة موضوعة فوق التل تبلغ طاقتها الكامنة 200 جول - فإن الكرة تتحرك فقط جزءًا من الطريق إلى أعلى التل وتتوقف وتعود في الاتجاه الذي جاءت منه. يتم تحويل الطاقة الكلية للكرة بالكامل إلى طاقة كامنة قبل أن تصل إلى قمة التل. لا نتوقع، حتى بعد المحاولات المتكررة، أن يتم العثور على كرة 100-J خارج التل. لذلك، فإن احتمال مرور الكرة فوق التل هو 0 بالضبط، واحتمال إعادتها إلى الوراء أو «انعكاسها» بواسطة التل هو بالضبط 1. لا تصل الكرة أبدًا فوق التل. إن وجود الكرة خلف التل أمر مستحيل أو «ممنوع بشدة».
ومع ذلك، وفقًا لميكانيكا الكم، فإن الكرة لها دالة موجة ويتم تحديد هذه الوظيفة في كل الفضاء. قد تكون وظيفة الموجة محلية للغاية، ولكن هناك دائمًا احتمال أن تظهر الكرة فجأة خلفها عندما تصطدم الكرة بالتل. في الواقع، يكون هذا الاحتمال ملموسًا إذا كانت «الحزمة الموجية» للكرة أوسع من الحاجز.
شاهد هذه المحاكاة التفاعلية لمحاكاة حفر الأنفاق.
في لغة ميكانيكا الكم، يتميز التل بحاجز محتمل. يتم وصف الحاجز المربع ذي الارتفاع المحدود بواسطة وظيفة الطاقة المحتملة التالية:
\ [U (x) =
\ ابدأ {الحالات}
0 و\ mbox {عندما} x < 0\\ [4pt] U_0, &\ mbox {when} 0\ leq x\ leq L\\ [4pt] 0, &\ mbox {when} x > L
\ end {الحالات}\ التسمية {piBpotential}\]
يظهر الحاجز المحتمل في الشكل\(\PageIndex{1}\). عندما يكون ارتفاع\(U_0\) الحاجز غير محدود، تكون حزمة الموجة التي تمثل جسيمًا كموميًا ساقطًا غير قادرة على اختراقه، ويرتد الجسيم الكمومي مرة أخرى من حدود الحاجز، تمامًا مثل الجسيم الكلاسيكي. عندما يكون عرض\(L\) الحاجز غير محدود وارتفاعه محدودًا، يمكن لجزء من حزمة الموجة التي تمثل جسيمًا كموميًا ساقطًا أن يرشح عبر حدود الحاجز ويهلك في النهاية بعد قطع مسافة ما داخل الحاجز.
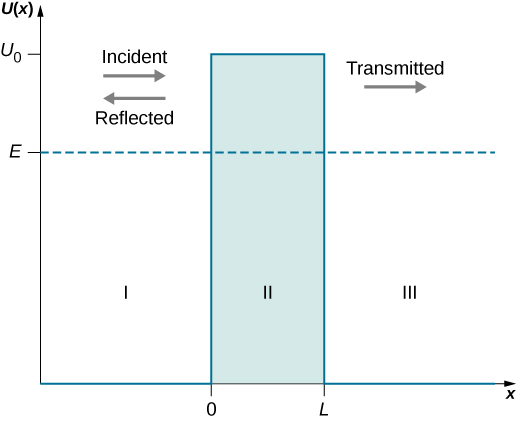
عندما يكون كل من العرض\(L\) والارتفاع\(U_0\) محدودين، يمكن لجزء من حزمة الموجة الكمومية الواقعة على جانب واحد من الحاجز اختراق حدود الحاجز ومواصلة حركته داخل الحاجز، حيث يتم تخفيفه تدريجيًا في طريقه إلى الجانب الآخر. يظهر جزء من حزمة الموجة الكمومية الساقطة في النهاية على الجانب الآخر من الحاجز في شكل حزمة الموجة المرسلة التي مرت عبر الحاجز. يعتمد مقدار الموجة الساقطة التي يمكن أن تمر عبر الحاجز على عرض\(L\) الحاجز وارتفاعه\(U_0\)، وعلى طاقة الجسيم\(E\) الكمومي الساقط على الحاجز. هذه هي فيزياء الأنفاق.
تم تحليل اختراق الحاجز بواسطة وظائف الموجة الكمومية لأول مرة نظريًا بواسطة فريدريش هوند في عام 1927، بعد وقت قصير من نشر Schrdinger للمعادلة التي تحمل اسمه. بعد عام، استخدم جورج جامو شكلية ميكانيكا الكم لشرح\(\alpha\) التحلل الإشعاعي للنواة الذرية كظاهرة حفر الأنفاق الكمومية. لقد أوضح اختراع الصمام الثنائي النفقي في عام 1957 أن حفر الأنفاق الكمومية مهم لصناعة أشباه الموصلات. في التقنيات النانوية الحديثة، تتم معالجة الذرات الفردية باستخدام معرفة الأنفاق الكمومية.
النفق والوظيفة الموجية
لنفترض أن شعاعًا موحدًا ومستقلًا عن الوقت من الإلكترونات أو الجسيمات الكمومية الأخرى ذات الطاقة التي\(E\) تنتقل على طول المحور x (في الاتجاه الإيجابي إلى اليمين) يواجه حاجزًا محتملاً موصوف في المعادلة\ ref {piBpotential}. السؤال هو: ما احتمال مرور جسيم فردي في الحزمة عبر الحاجز المحتمل؟ يمكن العثور على الإجابة من خلال حل مشكلة القيمة الحدية لمعادلة Schrdinger المستقلة عن الوقت لجسيم في الحزمة. يتم إعطاء الشكل العام لهذه المعادلة من خلال المعادلة\ ref {TISE}، والتي نعيد إنتاجها هنا:
\[-\frac{\hbar^2}{2m} \frac{d^2\psi(x)}{dx^2} + U(x)\psi(x) = E\psi(x), \label{TISE} \]
أين\(-\infty < x < +\infty\).
يتم تعريف الدالة المحتملة\(U(x)\) في المعادلة\ ref {TISE} بواسطة المعادلة\ ref {pibPotential}. نفترض أن الطاقة\(E\) المعطاة للجسيم الوارد أصغر\(U_0\) من ارتفاع الحاجز المحتمل\(E < U_0\)، لأن هذه هي الحالة الفيزيائية المثيرة للاهتمام. بمعرفة طاقة\(E\) الجسيم الوارد، تتمثل مهمتنا في حل المعادلة\ ref {TISE} لدالة\(\psi(x)\) مستمرة ولها مشتقات أولى مستمرة لجميع x. بمعنى آخر، نحن نبحث عن حل «سلس المظهر» (لأن هذه هي الطريقة التي تبدو بها وظائف الموجة) التي يمكن إعطاؤها تفسيرًا احتماليًا بحيث\(|\psi(x)|^2 = \psi^*(x)\psi(x)\) تكون الكثافة الاحتمالية.
نقسم المحور الحقيقي إلى ثلاث مناطق مع الحدود المحددة بالوظيفة المحتملة في المعادلة\ ref {pibPotential} (كما هو موضح في الشكل\(\PageIndex{1}\)) وننسخ المعادلة\ ref {TISE} لكل منطقة. تشتمل معادلة Schrdinger الثابتة\(x < 0\)، باستخدام\(\psi_{II}(x)\) الحل في المنطقة\(II\)\(0 \leq x \leq L\)، والحل في المنطقة\(x > L\)،\(III\) والحل في المنطقة، على الأشكال التالية في هذه المناطق الثلاث:\(\psi_I(x)\)\(I\)\(\psi_{III}(x)\)
\[-\dfrac{\hbar^2}{2m} \frac{d^2\psi_I(x)}{dx^2} = E\psi_I(x), \label{R1} \]
في المنطقة\(I\):\(-\infty < x < 0,\)
\[-\dfrac{\hbar^2}{2m} \frac{d^2\psi_{II}(x)}{dx^2} + U_0\psi_{II}(x) = E\psi_{II}(x) \label{R2} \]
في المنطقة\(II\):\(0 < x < L,\)
\[-\dfrac{\hbar^2}{2m} \frac{d^2\psi_{III}(x)}{dx^2} = E\psi_{III}(x) \label{R3} \]
في المنطقة\(III\):\(L < x < +\infty,\)
تتطلب حالة الاستمرارية عند حدود المنطقة ما يلي:
\[\psi_I(0) = \psi_{II}(0) \label{Bound1} \]
على الحدود بين المناطق\(I\) و\(II\)
و
\[\psi_{II}(L) = \psi_{III}(L) \label{Bound2} \]
على الحدود بين المناطق\(II\) و\(III\).
تتطلب حالة «النعومة» أن يكون المشتق الأول من المحلول مستمرًا عند حدود المنطقة:
\[ \left.\dfrac{d\psi_I(x)}{dx}\right|_{x = 0} = \left.\dfrac{d\psi_{II}(x)}{dx}\right|_{x = 0} \label{smooth1} \]
على الحدود بين المناطق\(I\) و\(II\)
و
\[ \left.\dfrac{d\psi_{II}(x)}{dx}\right|_{x = L} = \left.\dfrac{d\psi_{III}(x)}{dx}\right|_{x = L} \label{smooth2} \]
على الحدود بين المناطق\(II\) و\(III\).
في ما يلي، نجد الوظائف\(\psi_I(x), \, \psi_{II}(x)\)، و\(\psi_{III}(x)\).
يمكننا التحقق بسهولة (من خلال الاستبدال في المعادلة الأصلية والتمييز) من أنه في المناطق\(I\)\(III\)، يجب أن تكون الحلول في الأشكال العامة التالية:
\[\psi_I(x) = Ae^{+ikx} + Be^{-ikx} \label{Eq5A} \]
\[\psi_{III}(x) = Fe^{+ikx} + Ge^{-ikx} \label{Eq5B} \]
أين\(k = \sqrt{2mE}/\hbar\) يوجد رقم الموجة ويشير الأس المعقد إلى التذبذبات،
\[e^{\pm ikx} = \cos \, kx \pm i \, \sin \, kx. \nonumber \]
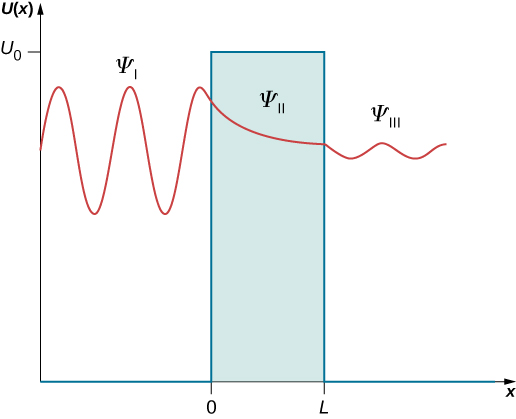
قد تكون الثوابت و\(A\)\(B\)\(F\)،\(G\) وفي المعادلات\ ref {Eq5A} و\ ref {Eq5B} معقدة. هذه الحلول موضحة في الشكل\(\PageIndex{2}\). في المنطقة الأولى، توجد موجتان - واحدة عرضية (تتحرك إلى اليمين) والأخرى تنعكس (تتحرك إلى اليسار) - لذلك قد لا تختفي أي من\(A\) الثوابت\(B\) وفي المعادلة\ ref {Eq5A}. في المنطقة الثالثة، توجد موجة واحدة فقط (تتحرك إلى اليمين)، وهي الموجة المرسلة، لذلك\(G\) يجب أن يكون الثابت صفرًا في المعادلة\ ref {Eq5B}،\(G = 0\). يمكننا أن نكتب صراحة أن الموجة الساقطة هي\(\psi_{in}(x) = Ae^{+ikx}\) وأن الموجة المنعكسة هي\(\psi_{ref}(x) = Be^{-ikx}\)، وأن الموجة المرسلة هي\(\psi_{tra}(x) = Fe^{+ikx}\). سعة الموجة الساقطة هي
\[ \begin{align*}|\psi_{in}(x)|^2 &= \psi_{in}^*(x)\psi_{in}(x) \\[4pt] &= (Ae^{+ikx})^*Ae^{+ikx} \\[4pt] &= A^*e^{-ikx}Ae^{+ikx} \\[4pt] &= A^*A = |A|^2. \end{align*} \nonumber \]
وبالمثل، فإن سعة الموجة المنعكسة هي\(|\psi_{ref}(x)|^2 = |B|^2\) وسعة الموجة المرسلة هي\(|\psi_{tra}(x)|^2 = |F|^2\). نعلم من نظرية الموجات أن مربع سعة الموجة يتناسب طرديًا مع شدة الموجة. إذا أردنا معرفة مقدار أنفاق الموجة الساقطة عبر الحاجز، فنحن بحاجة إلى حساب مربع سعة الموجة المرسلة. احتمالية الإرسال أو احتمالية النفق هي نسبة الكثافة المرسلة (\(|F|^2\)) إلى شدة الحادث (\(|A|^2\))، المكتوبة كـ
\[ \begin{align} T(L, E) &= \frac{|\psi_{tra}(x)|^2}{|\psi_{in}(x)|^2} \\[4pt] &= \frac{|F|^2}{|A|^2} \\[4pt] &= \left|\frac{F}{A}\right|^2 \label{trans} \end{align} \]
أين\(L\) هو عرض الحاجز\(E\) وهو الطاقة الكلية للجسيم. هذا هو احتمال أن يمر جسيم فردي في الحزمة الساقطة عبر الحاجز المحتمل. بشكل بديهي، نفهم أن هذا الاحتمال يجب أن يعتمد على ارتفاع الحاجز\(U_0\).
في المنطقة الثانية، يمكن إعادة ترتيب المصطلحات في معادلة المعادلة\ ref {R2} إلى
\[\frac{d^2\psi_{II}(x)}{dx^2} = \beta^2 \psi_{II}(x) \label{eq10} \]
أين\(\beta^2\) هو إيجابي لأن\(U_0 > E\) المعلمة\(\beta\) هي رقم حقيقي،
\[\beta^2 = \frac{2m}{\hbar^2}(U_0 - E). \label{eq20} \]
الحل العام للمعادلة\ ref {eq10} ليس تذبذبيًا (على عكس المناطق الأخرى) وهو في شكل أسس تصف التوهين التدريجي لـ\(\psi_{II}(x)\)،
\[\psi_{II}(x) = Ce^{-\beta x} + De^{+\beta x}. \label{eq25B} \]
يوضح الشكل نوعين من الحلول في المناطق الثلاث\(\PageIndex{2}\).
الآن نستخدم شروط الحدود لإيجاد معادلات للثوابت غير المعروفة. يتم استبدال المعادلات\ ref {Eq5A} و\ ref {eQ25b} في المعادلة\ ref {Bound1} لإعطاء
\[A + B = C + D. \nonumber \]
يتم استبدال المعادلات\ ref {eQ25b} و\ ref {Eq5B} في المعادلة\ ref {Bound2} لإعطاء
\[Ce^{-\beta L} + De^{+\beta L} = Fe^{+ik L}. \nonumber \]
وبالمثل، نستبدل المعادلات\ ref {Eq5A} و\ ref {eq25b} إلى المعادلة\ ref {smooth1}، ونميز ونحصل عليها
\[-ik(A - B) = \beta(D - C). \nonumber \]
وبالمثل، فإن معادلة الشرط الحدودي\ ref {smooth2} تقرأ بشكل صريح
\[\beta (De^{+\beta L} - Ce^{-\beta L}) = +ikFe^{+ikL}. \nonumber \]
لدينا الآن أربع معادلات لخمسة ثوابت غير معروفة. ومع ذلك، نظرًا لأن الكمية التي نسعى إليها هي معامل الإرسال (\(T\))، المحدد في المعادلة\ ref {trans} بالكسر\(F/A\)، فإن عدد المعادلات صحيح تمامًا لأنه عندما نقسم كل من المعادلات المذكورة أعلاه\(A\)، ينتهي بنا الأمر إلى وجود أربعة كسور غير معروفة فقط: \(B/A\)،\(C/A\)،\(D/A\)، و\(F/A\)، يمكن التخلص من ثلاثة منها للعثور عليها\(F/A\). الجبر الفعلي الذي يؤدي إلى التعبير طويل\(F/A\) جدًا، ولكن يمكن القيام به إما يدويًا أو بمساعدة برامج الكمبيوتر. النتيجة النهائية هي
\[\frac{F}{A} = \frac{e^{-ikL}}{\cosh \, (\beta L) + i (\gamma /2) \, \sinh \, (\beta L)}. \label{eq40} \]
في اشتقاق المعادلة\ ref {eq40}، لتجنب الفوضى\(\gamma \equiv \beta/k - k/\beta\)، نستخدم البدائل وتعريف الدوال القطعية:
\[\cosh \, y = \frac{e^y + e^{-y}}{2} \nonumber \]
و
\[\sinh \, y = \frac{e^y - e^{-y}}{2}. \nonumber \]
نستبدل المعادلة\ ref {eq40} بالمعادلة\ ref {trans} ونحصل على التعبير الدقيق لمعامل الإرسال للحاجز،
\[T(L,E) = \left(\frac{F}{A}\right)^*\frac{F}{A} = \frac{e^{+ikL}}{\cosh \, (\beta L) - i (\gamma /2) \, \sinh \, (\beta L)} \cdot \frac{e^{-ikL}}{\cosh \, (\beta L) + i (\gamma /2) \, \sinh \, (\beta L)}. \nonumber \]
أو
\[T(L,E) = \frac{1}{\cosh^2 \, (\beta L) + (\gamma /2)^2 \, \sinh^2 \, (\beta L)}. \label{eqTrans1} \]
حيث
\[\left(\frac{\gamma}{2}\right)^2 = \frac{1}{4}\left( \frac{1 - E/U_0}{E/U_0} + \frac{E/U_0}{1 - E/U_0} - 2\right). \nonumber \]
بالنسبة للحاجز العريض والعالي الذي ينقل بشكل سيئ، يمكن تقريب المعادلة\ ref {eQTrans1} بواسطة
\[T(L,E) \approx 16 \frac{E}{U_0}\left(1 - \dfrac{E}{U_0}\right) e^{-2\beta L}. \label{eqTrans2} \]
سواء كان التعبير الدقيق (Equation\ ref {eqTrans1}) أو التعبير التقريبي (Equation\ ref {eQTrans2})، نرى أن تأثير النفق يعتمد بشدة على عرض\(L\) الحاجز المحتمل. في المختبر، يمكننا ضبط كل من الارتفاع\(U_0\) المحتمل والعرض\(L\) لتصميم أجهزة النانو ذات معاملات الإرسال المرغوبة.
يتم عزل سلكين نانويين نحاسيين بطبقة نانوية من أكسيد النحاس توفر حاجزًا محتملاً يبلغ 10.0-EV. قم بتقدير احتمالية حفر الأنفاق بين الأسلاك النانوية بواسطة إلكترونات بقوة 7.00-eV من خلال طبقة أكسيد بسمك 5.00-nm. ماذا لو انخفض سمك الطبقة إلى 1.00 nm فقط؟ ماذا لو زادت طاقة الإلكترونات إلى 9.00 eV؟
إستراتيجية
عند معالجة طبقة الأكسيد العازل كحاجز محتمل ذو ارتفاع محدود، نستخدم Equation\ ref {eQTrans2}. نحدد\(U_0 = 10.0 \, eV, \, E_1 = 7.00 \, eV, \, E_2 = 9.00 \, eV, \, L_1 = 5.00 \, nm\)، و\(L_2 = 1.00 \, nm\). نحن نستخدم المعادلة\ ref {eq20} لحساب الأس. نحتاج أيضًا إلى كتلة الراحة للإلكترون\(m = 511 \, keV/c^2\) وثابت بلانك\(\hbar = 0.1973 \, keV \cdot nm/c\). من المعتاد أن يتعامل هذا النوع من التقديرات مع الكميات الصغيرة جدًا التي غالبًا ما تكون غير مناسبة للآلات الحاسبة المحمولة. لإجراء تقديرات صحيحة للطلبات، نقوم بإجراء التحويل\(e^y = 10^{y/ln \, 10}\).
الحل
الثوابت:
\[\frac{2m}{\hbar^2} = \frac{2(511 \, keV/c^2)}{(0.1973 \, keV \cdot nm/c^2)^2} = 26,254 \frac{1}{keV \cdot (nm)^2}, \nonumber \]
\[\beta = \sqrt{\frac{2m}{\hbar^2}(U_0 - E)} = \sqrt{26,254\frac{(10.0 \, eV - E)}{keV \cdot (nm)^2}} = \sqrt{26.254(10.00 - E)/eV} \frac{1}{nm}.\nonumber \]
لإلكترون منخفض الطاقة مع\(E_1 = 7.00 \, eV\):
\[\beta_1 = \sqrt{26.254(10.00 \, eV - E_1)/eV}\frac{1}{nm} = \sqrt{26.254(10.00 - 7.00)}\frac{1}{nm} = \frac{8.875}{nm},\nonumber \]
\[T(L,E) = 16\frac{E_1}{U_0}\left(1 - \frac{E_1}{U_0}\right)e^{-2\beta_1L} = 16\frac{7}{10}\left(1 - \frac{7}{10}\right)e^{-17.75 \, L/nm} = 3.36 \, e^{-17.75 \, L/nm}\nonumber \]
لإلكترون عالي الطاقة مع\(E_2 = 9.00 \, eV\):
\[\beta_2 = \sqrt{26.254(10.00 \, eV - E_2)/eV}\frac{1}{nm} = \sqrt{26.254 (10.00 - 9.00)}\frac{1}{nm} = \frac{5.124}{nm},\nonumber \]
\[T(L,E_2) = 16\frac{E_2}{U_0}\left( 1 - \frac{E_2}{U_0}\right) e^{-2\beta_2 L} = 16 \frac{9}{10} \left(1 - \frac{9}{10}\right) e^{-10.25 \, L/nm} = 1.44 \, e^{-10.25 \, L/nm}\nonumber \]
للحصول على حاجز واسع مع\(L_1 = 5.00 \, nm\):
\[T(L_1,E_1) = 3.36 e^{-17.75 \, L_1/nm} = 3.36 e^{-17.75 \cdot 5.00 nm/nm} = 3.36e^{-88} = 3.36(6.2 \times 10^{-39}) = 2.1\% \times 10^{-36}\nonumber \]
\[T(L_1,E_2) = 1.44 e^{-10.25 \, L_1/nm} = 1.44 e^{-10.25 \cdot 5.00 \, nm/nm} = 1.44^{-51.2} = 1.44(5.81 \times 10^{-12}) = 8.36\% \times 10^{-25}\nonumber \]
للحصول على حاجز أضيق مع\(L_2 = 1.00 \, nm\):
\[T(L_2,E_1) = 3.36e^{−17.75 \, L_2/nm} = 3.36 e^{−17.75 \cdot 1.00 \, nm/nm} = 3.36 e^{−17.75} = 3.36(5.1 \times 10^{−7}) = 1.7\% \times 10^{−4},\nonumber \]
\[T(L_2,E_2) = 1.44e^{−10.25 \, L_2/nm} = 1.44e^{-10.25 \cdot 1.00 \, nm/nm} = 1.44e^{−10.25} = 1.44(3.53 \times 10^{−5}) = 5.09\% \times 10^{-7}.\nonumber \]
الدلالة
نرى من هذه التقديرات أن احتمالية حفر الأنفاق تتأثر بعرض الحاجز المحتمل أكثر من طاقة الجسيم الساقط. في تقنيات اليوم، يمكننا معالجة الذرات الفردية على الأسطح المعدنية لإنشاء حواجز محتملة تمثل أجزاء من النانومتر، مما يؤدي إلى ظهور تيارات نفقية قابلة للقياس. يعد مجهر المسح النفقي (STM) أحد التطبيقات العديدة لهذه التقنية، والذي نناقشه لاحقًا في هذا القسم.
يسقط بروتون ذو طاقة حركية تبلغ 1.00 eV على حاجز مربع محتمل بارتفاع 10.00 eV. إذا كان للبروتون نفس احتمال الإرسال مثل إلكترون له نفس الطاقة، فما الذي يجب أن يكون عرض الحاجز بالنسبة لعرض الحاجز الذي يواجهه الإلكترون؟
- إجابة
-
\[L_{proton}/L_{electron} = \sqrt{m_e/m_p} = 2.3\% \nonumber \]
الاضمحلال الإشعاعي
في عام 1928، حدد Gamow الأنفاق الكمومية كآلية مسؤولة عن التحلل الإشعاعي للنواة الذرية. لاحظ أن بعض نظائر الثوريوم واليورانيوم والبزموت تتفكك عن طريق انبعاث جزيئات ألفا (وهي ذرات هيليوم مؤينة بشكل مضاعف أو، ببساطة، نوى الهيليوم). في عملية إصدار جسيم ألفا، تتحول النواة الأصلية إلى نواة جديدة يقل عدد النيوترونات واثنين من البروتونات عن النواة الأصلية. تحتوي جزيئات ألفا المنبعثة من أحد النظائر على نفس الطاقات الحركية تقريبًا. عندما ننظر إلى الاختلافات في هذه الطاقات بين نظائر العناصر المختلفة، فإن أقل طاقة حركية هي حوالي 4 MeV وأعلاها حوالي 9 MeV، لذا فإن هذه الطاقات لها نفس الترتيب من حيث الحجم. هذا هو المكان الذي تنتهي فيه أوجه التشابه بين النظائر المختلفة.
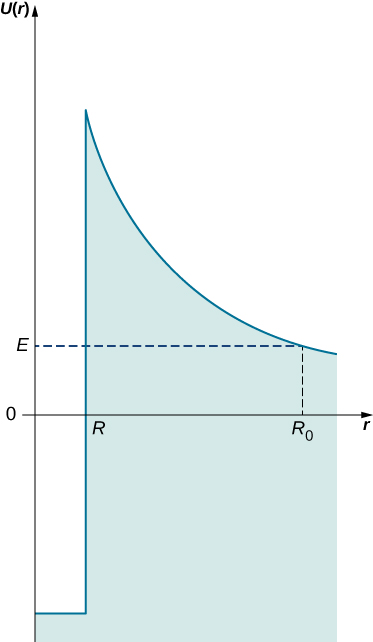
عندما نفحص فترات نصف العمر (نصف العمر هو الوقت الذي تفقد فيه العينة المشعة نصف نواتها بسبب التحلل)، تختلف النظائر المختلفة بشكل كبير. على سبيل المثال، يبلغ نصف عمر البولونيوم 214 160 ميكروثانية ونصف عمر اليورانيوم 4.5 مليار سنة. شرح Gamow هذا الاختلاف من خلال النظر في نموذج «الصندوق الكروي» للنواة، حيث يمكن لجسيمات ألفا أن ترتد ذهابًا وإيابًا بين الجدران كجزيئات حرة. يتم توفير الحبس من خلال إمكانات نووية قوية على جدار كروي للصندوق. ومع ذلك، فإن سمك هذا الجدار ليس بلا حدود ولكنه محدود، لذلك من حيث المبدأ، فإن الجسيمات النووية لديها فرصة للهروب من هذا الحبس النووي. يوجد على الجدار الداخلي للحاجز المحصور إمكانات نووية عالية تحافظ على جسيم ألفا في حجرة صغيرة. ولكن عندما يخرج جسيم ألفا إلى الجانب الآخر من هذا الجدار، فإنه يخضع لصد كولوم الكهروستاتيكي ويبتعد عن النواة. هذه الفكرة موضحة في الشكل\(\PageIndex{3}\). يعتمد عرض\(L\) الحاجز المحتمل الذي يفصل جسيم ألفا عن العالم الخارجي على الطاقة الحركية للجسيم\(E\). هذا العرض هو المسافة بين النقطة المحددة بنصف القطر\(R\) النووي والنقطة التي يظهر\(R_0\) فيها جسيم ألفا على الجانب الآخر من الحاجز\(L = R_0 - R\). على مسافة بعيدة\(R_0\)، يجب أن تتطابق طاقتها الحركية على الأقل مع الطاقة الكهروستاتيكية للتنافر،\(E = (4\pi\epsilon_0)^{-1}Ze^2/R_0\) (حيث +Ze هي شحنة النواة). بهذه الطريقة يمكننا تقدير عرض الحاجز النووي،
\[L = \frac{e^2}{4\pi\epsilon_0} \frac{Z}{E} - R. \nonumber \]
نرى من هذا التقدير أنه كلما زادت طاقة جسيم ألفا، كلما كان عرض الحاجز الذي سيتم النفق عبره أضيق. نعلم أيضًا أن عرض الحاجز المحتمل هو أهم عامل في احتمالية حفر الأنفاق. وبالتالي، فإن الجسيمات ألفا عالية الطاقة لديها فرصة جيدة للهروب من النواة، وبالنسبة لهذه النوى، فإن نصف عمر التفكك النووي قصير. لاحظ أن هذه العملية غير خطية للغاية، مما يعني أن الزيادة الطفيفة في طاقة الجسيمات ألفا لها تأثير تعزيز كبير بشكل غير متناسب على احتمالية حفر الأنفاق، وبالتالي على تقصير عمر النصف. وهذا يفسر سبب كون نصف عمر البولونيوم الذي ينبعث منه جزيئات ألفا من 8 MeV هو مئات المللي ثانية فقط، ونصف عمر اليورانيوم الذي ينبعث منه جزيئات ألفا من 4 MeV هو مليارات السنين.
الانبعاثات الميدانية
الانبعاثات الميدانية هي عملية انبعاث إلكترونات من الأسطح الموصلة بسبب المجال الكهربائي الخارجي القوي الذي يتم تطبيقه في الاتجاه الطبيعي للسطح (الشكل\(\PageIndex{4}\)). كما نعلم من دراستنا للمجالات الكهربائية في الفصول السابقة، يتسبب المجال الكهربائي الخارجي المطبق في انتقال الإلكترونات في الموصل إلى سطحه والبقاء هناك طالما أن المجال الخارجي الحالي ليس قويًا بشكل مفرط. في هذه الحالة، لدينا إمكانات كهربائية ثابتة في جميع أنحاء الجزء الداخلي من الموصل، بما في ذلك سطحه. في لغة الطاقة الكامنة، نقول أن الإلكترون داخل الموصل لديه طاقة كامنة ثابتة\(U(x) - -U_0\) (هنا، تعني x داخل الموصل).
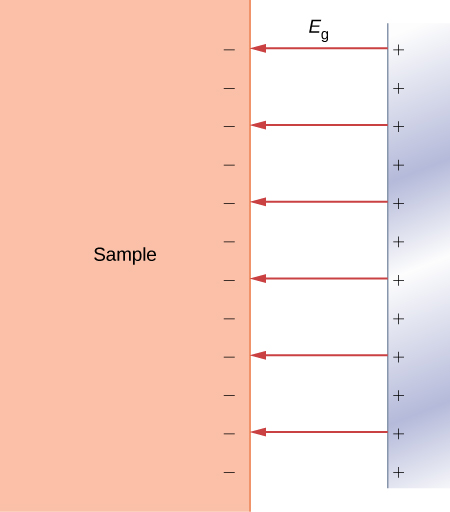
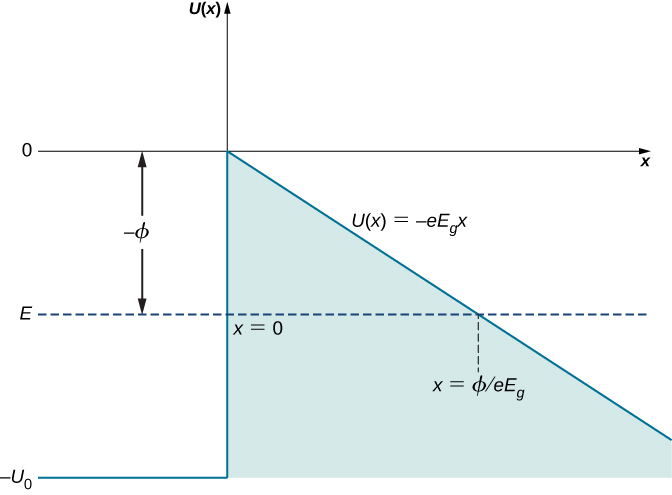
في الحالة الممثلة في الشكل\(\PageIndex{4}\)، حيث يكون المجال الكهربائي الخارجي موحدًا وله حجم\(E_g\)، إذا حدث وجود إلكترون خارج الموصل على مسافة x من سطحه، فيجب أن تكون طاقته الكامنة\(U(x) = -eE_gx\) (هنا، تشير x إلى المسافة إلى السطح). بأخذ نقطة الأصل على السطح، أي\(x = 0\) موقع السطح، يمكننا تمثيل الطاقة الكامنة لإلكترونات التوصيل في المعدن باعتبارها حاجز الطاقة المحتمل الموضح في الشكل\(\PageIndex{5}\). في حالة عدم وجود المجال الخارجي، تصبح الطاقة الكامنة حاجزًا متدرجًا يتم تحديده بواسطة\(U(x \leq 0) = -U_0\) وبواسطة\(U(x > 0) = 0\).
عندما يكون المجال الكهربائي الخارجي قويًا، قد تنفصل إلكترونات التوصيل الموجودة على السطح عنه وتتسارع على طول خطوط المجال الكهربائي في اتجاه مضاد للمجال الخارجي، بعيدًا عن السطح. باختصار، قد تتسرب إلكترونات التوصيل من السطح. يمكن فهم الانبعاثات الميدانية على أنها النفق الكمي لإلكترونات التوصيل من خلال الحاجز المحتمل على سطح الموصل. يشبه المبدأ الفيزيائي في العمل هنا إلى حد كبير آلية انبعاث ألفا من نواة مشعة.
لنفترض أن إلكترون التوصيل يحتوي على طاقة حركية E (متوسط الطاقة الحركية للإلكترون في المعدن هو وظيفة العمل للمعدن ويمكن قياسها، كما تمت مناقشته للتأثير الكهروضوئي في الفوتونات وموجات المادة)، ويمكن أن يكون المجال الكهربائي الخارجي محليًا يقترب من مجال قوة كهربائي موحد\(E_g\). عرض L للحاجز المحتمل الذي يجب أن يتجاوزه الإلكترون هو المسافة من سطح الموصل إلى النقطة خارج السطح حيث تتطابق طاقته الحركية مع قيمة طاقته الكامنة في المجال الخارجي. في الشكل\(\PageIndex{5}\)، يتم قياس هذه المسافة على طول الخط الأفقي المتقطع\(U(x) = E\) من\(x = 0\) إلى التقاطع\(U(x) = -eE_gx\)، وبالتالي فإن عرض الحاجز هو
\[L = \frac{e^{-1}E}{E_g} = \frac{e^{-1}\phi}{E_g} \nonumber \]
نرى أن L يتناسب عكسيًا مع\(E_g\) قوة المجال الخارجي. عندما نزيد من قوة المجال الخارجي، يصبح الحاجز المحتمل خارج الموصل أكثر حدة ويقل عرضه للإلكترون ذي الطاقة الحركية المعينة. في المقابل، يصبح احتمال مرور الإلكترون عبر الحاجز (سطح الموصل) أكبر بشكل كبير. تشكل الإلكترونات التي تظهر على الجانب الآخر من هذا الحاجز تيارًا (تيار إلكتروني نفقي) يمكن اكتشافه فوق السطح. يتناسب تيار الإلكترون النفقي مع احتمال حفر الأنفاق. تعتمد احتمالية حفر الأنفاق بشكل غير خطي على عرض الحاجز L، ويمكن تغيير L عن طريق التعديل\(E_g\). لذلك، يمكن ضبط تيار الإلكترون النفقي عن طريق ضبط قوة المجال الكهربائي الخارجي على السطح. عندما تكون قوة المجال الكهربائي الخارجي ثابتة، فإن تيار الإلكترون النفقي له قيم مختلفة عند ارتفاعات مختلفة L فوق السطح.
إن ظاهرة حفر الأنفاق الكمومية على الأسطح المعدنية، التي وصفناها للتو، هي المبدأ المادي وراء تشغيل مجهر المسح النفقي (STM)، الذي اخترعه جيرد بينيغ وهاينريش روهرر في عام 1981. يتكون جهاز STM من طرف المسح (إبرة، عادة ما تكون مصنوعة من التنجستن أو البلاتين أو الإيريديوم أو الذهب)؛ جهاز كهرضغطي يتحكم في ارتفاع الطرف في نطاق نموذجي من 0.4 إلى 0.7 نانومتر فوق السطح المراد مسحه ضوئيًا؛ بعض الأجهزة التي تتحكم في حركة الطرف على طول السطح؛ وجهاز كمبيوتر لعرض الصور. بينما يتم الاحتفاظ بالعينة عند تحيز مناسب للجهد، يتحرك طرف المسح على طول السطح (الشكل\(\PageIndex{6}\)) ويتم تسجيل تيار الإلكترون النفقي بين الطرف والسطح في كل موضع.
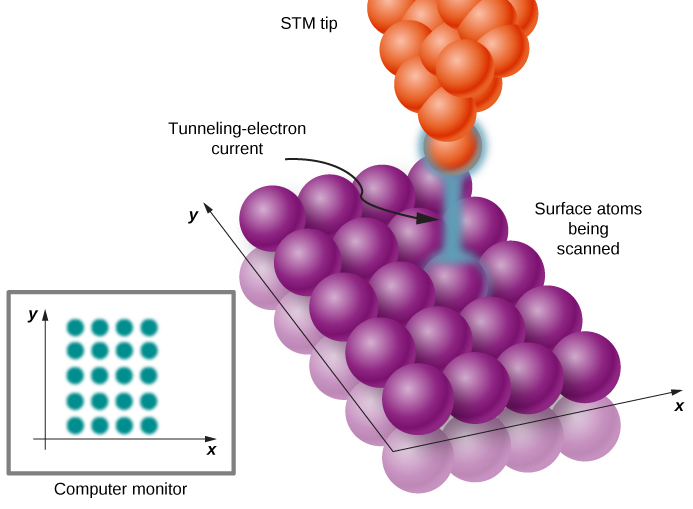
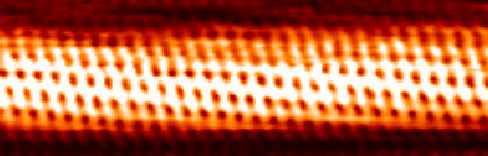
يعتمد مقدار التيار على احتمال نفق الإلكترون من السطح إلى الطرف، والذي بدوره يعتمد على ارتفاع الطرف فوق السطح. وبالتالي، عند كل موضع طرف، يتم قياس المسافة من الطرف إلى السطح عن طريق قياس عدد الإلكترونات التي تتدفق من السطح إلى الطرف. يمكن أن تعطي هذه الطريقة دقة غير مسبوقة تبلغ حوالي 0.001 نانومتر، أي حوالي 1٪ من متوسط قطر الذرة. بهذه الطريقة، يمكننا رؤية ذرات فردية على السطح، كما في صورة الأنبوب النانوي الكربوني في الشكل\(\PageIndex{7}\).
النفق الكمومي الرنيني
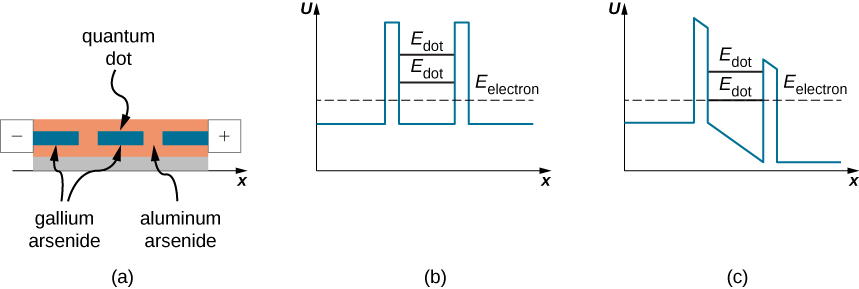
يحتوي حفر الأنفاق الكمومية على العديد من التطبيقات في أجهزة أشباه الموصلات مثل مكونات الدوائر الإلكترونية أو الدوائر المتكاملة المصممة على المقاييس النانوية؛ ومن هنا جاء مصطلح «تقنية النانو». على سبيل المثال، يمكن تحقيق الصمام الثنائي (عنصر الدائرة الكهربائية الذي يتسبب في اختلاف تيار الإلكترون في اتجاه واحد عن التيار في الاتجاه المعاكس، عندما يتم عكس قطبية جهد التحيز) من خلال تقاطع نفقي بين نوعين مختلفين من المواد شبه الموصلة. في مثل هذا الصمام الثنائي النفقي، تمر الإلكترونات عبر حاجز محتمل واحد عند اتصال بين اثنين من أشباه الموصلات المختلفة. عند التقاطع، يتغير تيار الإلكترون النفقي بشكل غير خطي مع فرق الجهد المطبق عبر الوصلة وقد ينخفض بسرعة مع زيادة جهد التحيز. هذا على عكس سلوك قانون أوم الذي نعرفه في الدوائر المنزلية. هذا النوع من السلوك السريع (الناجم عن الأنفاق الكمومية) مرغوب فيه في الأجهزة الإلكترونية عالية السرعة.
يستخدم نوع آخر من أجهزة النانو الإلكترونية الأنفاق الرنانة للإلكترونات من خلال الحواجز المحتملة التي تحدث في النقاط الكمومية. النقطة الكمومية هي منطقة صغيرة من البلورة النانوية شبه الموصلة التي تنمو، على سبيل المثال، في بلورة زرنيخيد السيليكون أو الألومنيوم. \(\PageIndex{8a}\)يوضِّح الشكل نقطة كمية من زرنيخيد الغاليوم مُضمَّنة في رقاقة زرنيخيد الألومنيوم. تعمل منطقة النقطة الكمومية كبئر محتمل بارتفاع محدود (الشكل\(\PageIndex{8b}\)) يحتوي على حاجزين محتملين ذوي ارتفاع محدود عند حدود النقاط. وبالمثل، بالنسبة للجسيم الكمومي في صندوق (أي بئر إمكانات غير محدودة)، يتم تحديد الطاقات المنخفضة لجسيم كمي محاصر في بئر جهد ذي ارتفاع محدود. الفرق بين إمكانات الصندوق وإمكانات البئر هو أن الجسيم الكمومي في الصندوق يحتوي على عدد لا حصر له من الطاقات الكمية ويتم احتجازه في الصندوق إلى أجل غير مسمى، في حين أن الجسيم الكمومي المحاصر في بئر محتمل لديه عدد محدود من مستويات الطاقة الكمية ويمكنه المرور عبر الإمكانات. حواجز عند حدود البئر إلى خارج البئر. وبالتالي، فإن النقطة الكمومية من زرنيخيد الغاليوم الموجودة في زرنيخيد الألومنيوم هي بئر محتملة يتم فيها قياس الطاقات المنخفضة للإلكترون، كما هو موضح\(E_{dot}\) في الجزء (ب) في الشكل. عندما لا تتطابق طاقة\(E_{electron}\) الإلكترون في المنطقة الخارجية من النقطة مع طاقته\(E_{dot}\) التي ستكون في النقطة، لا يمر الإلكترون عبر منطقة النقطة ولا يوجد تيار من خلال عنصر الدائرة هذا، حتى لو تم الاحتفاظ به عند فرق الجهد الكهربائي (تحيز). ومع ذلك، عندما يتغير تحيز الجهد هذا بطريقة تؤدي إلى خفض أحد الحواجز، بحيث\(E_{dot}\) يتم محاذاته، كما هو موضح في الجزء (ج) من الشكل، يتدفق تيار الإلكترون عبر النقطة.\(E_{electron}\) عندما يزداد تحيز الجهد الآن، يتم فقدان هذه المحاذاة ويتوقف التيار عن التدفق. عندما يزداد تحيز الجهد أكثر، يصبح نفق الإلكترون غير محتمل حتى يصل جهد التحيز إلى قيمة تتطابق فيها طاقة الإلكترون الخارجية مع مستوى طاقة الإلكترون التالي في النقطة. تعني كلمة «الرنين» في اسم الجهاز أن تيار الإلكترون النفقي يحدث فقط عندما يتم مطابقة مستوى طاقة محدد عن طريق ضبط تحيز الجهد المطبق، كما هو الحال في آلية تشغيل الصمام الثنائي النفقي بالرنين الموصوف للتو. تُستخدم الصمامات الثنائية النفقية للرنين كمفاتيح نانوية فائقة السرعة.