7.6: المذبذب التوافقي الكمي
- Page ID
- 196757
في نهاية هذا القسم، ستكون قادرًا على:
- وصف نموذج المذبذب التوافقي الكمي
- حدد الاختلافات بين النماذج الكلاسيكية والكمومية للمذبذب التوافقي
- اشرح المواقف المادية التي يتطابق فيها النموذج الكلاسيكي والنموذج الكمي
توجد التذبذبات في جميع أنحاء الطبيعة، في أشياء مثل الموجات الكهرومغناطيسية والجزيئات المهتزة والتأثير اللطيف ذهابًا وإيابًا لفرع الشجرة. في الفصول السابقة، استخدمنا ميكانيكا نيوتن لدراسة التذبذبات العيانية، مثل الكتلة على الزنبرك والبندول البسيط. في هذا الفصل، نبدأ بدراسة الأنظمة المتذبذبة باستخدام ميكانيكا الكم. نبدأ بمراجعة المذبذب التوافقي الكلاسيكي.
المذبذب التوافقي الكلاسيكي
المذبذب التوافقي البسيط هو جسيم أو نظام يخضع لحركة توافقية حول موضع التوازن، مثل جسم تهتز كتلته على زنبرك. في هذا القسم، ننظر في التذبذبات ذات البعد الواحد فقط. لنفترض أن الكتلة تتحرك ذهابًا وإيابًا على طول\(x\) الاتجاه - حول موضع التوازن،\(x = 0\). في الميكانيكا الكلاسيكية، يتحرك الجسيم استجابة لقوة استعادة خطية تُعطى بواسطة\(F_x = -kx\)، أين\(x\) إزاحة الجسيم من موضع توازنه. تحدث الحركة بين نقطتي دوران\(x \pm A\)، حيث تشير A إلى سعة الحركة. يختلف موضع الجسم دوريًا بمرور الوقت مع التردد الزاوي\(\omega = \sqrt{k/m}\)، والذي يعتمد على الكتلة m للمذبذب وعلى ثابت\(k\) القوة للقوة الصافية، ويمكن كتابته كـ
\[x(t) = A \, \cos (\omega t + \phi). \label{7.52} \]
الطاقة الكلية\(E\) للمذبذب هي مجموع طاقته الحركية\(K = mu^2/2\) والطاقة الكامنة المرنة للقوة\(U(x) = kx^2/2\)،
\[E = \dfrac{1}{2} mu^2 + \dfrac{1}{2}kx^2. \label{7.53} \]
عند نقاط التحول\(x = \pm A\)، تكون سرعة المذبذب صفرًا؛ لذلك، عند هذه النقاط، تكون طاقة التذبذب فقط في شكل طاقة كامنة\(E = kA^2/2\). مخطط الطاقة الكامنة\(U(x)\) للمذبذب مقابل موضعه\(x\) هو المكافئ (الشكل\(\PageIndex{1}\)). دالة الطاقة الكامنة هي دالة تربيعية لـ\(x\)، تُقاس فيما يتعلق بموضع التوازن. في نفس الرسم البياني، نرسم أيضًا الطاقة الكلية\(E\) للمذبذب، كخط أفقي يعترض المكافئ عند\(x = \pm A\). ثم\(K\) يتم تمثيل الطاقة الحركية على أنها المسافة الرأسية بين خط الطاقة الكلية والقطع المكافئ للطاقة الكامنة.
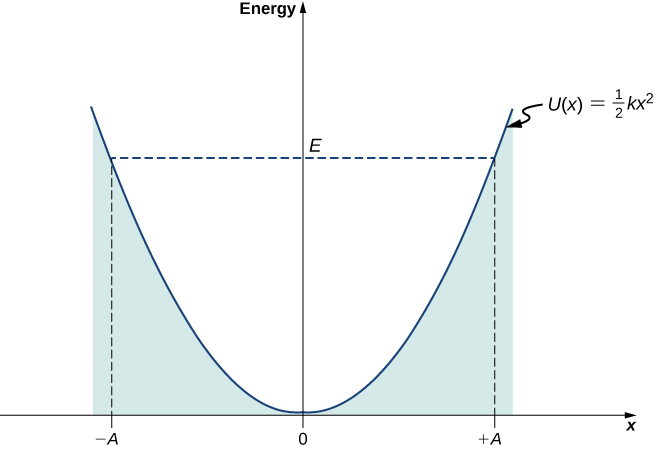
في هذا المخطط، تقتصر حركة المذبذب الكلاسيكي على المنطقة التي تكون فيها طاقته الحركية غير سالبة، وهو ما تقوله معادلة علاقة الطاقة\ ref {7.53}. من الناحية الفيزيائية، يعني ذلك أنه لا يمكن أبدًا العثور على المذبذب الكلاسيكي خارج نقاط التحول، وتعتمد طاقته فقط على مدى بُعد نقاط التحول عن موضع توازنه. تتغير طاقة المذبذب الكلاسيكي بطريقة مستمرة. أقل طاقة قد يمتلكها المذبذب الكلاسيكي هي صفر، وهو ما يتوافق مع الحالة التي يكون فيها الجسم في حالة سكون في وضع الاتزان. حالة الطاقة الصفرية للمذبذب الكلاسيكي تعني ببساطة عدم وجود تذبذبات وعدم وجود حركة على الإطلاق (جسيم كلاسيكي يجلس في أسفل البئر المحتمل في الشكل\(\PageIndex{1}\)). عندما يتذبذب جسم، بغض النظر عن حجم طاقته أو صغرها، فإنه يقضي أطول وقت بالقرب من نقاط الانعطاف، لأن هذا هو المكان الذي يتباطأ فيه ويعكس اتجاه حركته. لذلك، فإن احتمال العثور على مذبذب كلاسيكي بين نقاط التحول هو الأعلى بالقرب من نقاط التحول والأدنى عند موضع التوازن. (لاحظ أن هذا ليس بيانًا لتفضيل الكائن للذهاب إلى طاقة أقل. إنه بيان حول مدى سرعة تحرك الكائن عبر مناطق مختلفة.)
المذبذب التوافقي الكمي
مشكلة واحدة في هذه الصيغة الكلاسيكية هي أنها ليست عامة. لا يمكننا استخدامه، على سبيل المثال، لوصف اهتزازات الجزيئات ثنائية الذرة، حيث تكون التأثيرات الكمومية مهمة. الخطوة الأولى نحو الصيغة الكمومية هي استخدام التعبير الكلاسيكي\(k = m\omega^2\) للحد من ذكر ثابت «الربيع» بين الذرات. بهذه الطريقة يمكن كتابة وظيفة الطاقة المحتملة في شكل أكثر عمومية،
\[U(x) = \dfrac{1}{2}m \omega^2 x^2. \label{7.54} \]
يؤدي الجمع بين هذا التعبير ومعادلة Schrdinger المستقلة عن الوقت إلى
\[-\dfrac{\hbar}{2m} \dfrac{d^2 \psi(x)}{dx^2} + \dfrac{1}{2}m\omega^2 x^2 \psi(x) = E\psi (x). \label{7.55} \]
لحل المعادلة\ ref {7.55}، أي للعثور على الطاقات\(E\) المسموح بها ووظائف الموجة المقابلة لها\(\psi (x) \) - نطلب أن تكون وظائف الموجة متماثلة حول\(x = 0\) (الجزء السفلي من البئر المحتمل) وأن تكون قابلة للتطبيع. تضمن هذه الشروط أن كثافة الاحتمالية\(|\psi (x)|^2\) يجب أن تكون محدودة عند دمجها على النطاق الكامل لـ x من\(-\infty\) إلى\(+\infty\). كيفية حل المعادلة\ ref {7.55} هي موضوع دورة أكثر تقدمًا في ميكانيكا الكم؛ هنا، نستشهد ببساطة بالنتائج. الطاقات المسموح بها هي
\[ \begin{align} E_n &= \left(n + \dfrac{1}{2}\right) \hbar \omega \\[5pt] &= \dfrac{2n + 1}{2} \hbar \omega \label{7.56} \end{align} \]
مع\(n = 0,1,2,3,...\)
وظائف الموجة التي تتوافق مع هذه الطاقات (الحالات الثابتة أو حالات الطاقة المحددة) هي
\[\psi_n (x) = N_n e^{-\beta^2 x^2/2} H_n (\beta x), \, n = 0,1,2,3, ... \label{7.57} \]
حيث\(\beta = \sqrt{m\omega/\hbar}\)\(N_n\) يكون التطبيع ثابتًا،\(H_n(y)\) وهو عبارة عن دالة متعددة الحدود\(n\) تسمى متعددة الحدود الهرمية. وكثيرات حدود هيرميت الأربعة الأولى هي:
- \(H_0 (y) = 1\)
- \(H_1 (y) = 2y\)
- \(H_2 (y) = 4y^2 - 2\)
- \(H_3 (y) = 8y^3 - 12 y.\)
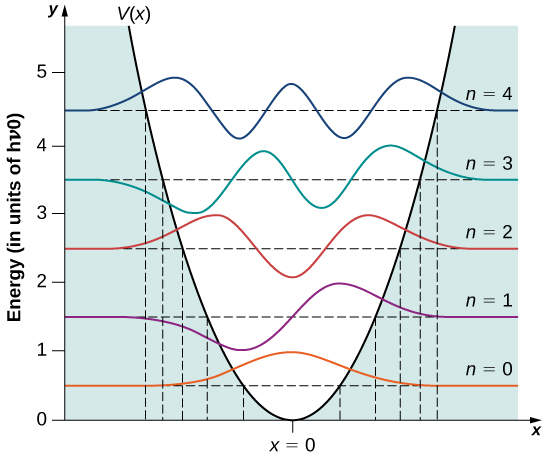
يتضمن الشكل بعض نماذج الدوال الموجية\(\PageIndex{2}\). كلما زادت قيمة الرقم الأساسي، تتناوب الحلول بين الوظائف الزوجية والوظائف الفردية\(x = 0\).
أوجد سعة التذبذبات\(A\) لمذبذب كلاسيكي بطاقة تساوي طاقة المذبذب الكمومي في الحالة الكمومية\(n\).
إستراتيجية
لتحديد السعة\(A\)، قمنا بتعيين الطاقة الكلاسيكية التي\(E = kx^2/2 = m\omega^2 \, A^2/2\) تساوي\(E_n\) المعطاة بالمعادلة\ ref {7.56}.
الحل
نحصل على
\[\begin{align} E_n &= m\omega^2 A_n^2/2 \nonumber \\[5pt] A_n &= \sqrt{\dfrac{2}{m\omega^2}E_n} \nonumber \\[5pt] &= \sqrt{\dfrac{2}{m\omega^2} \dfrac{2n + 1}{2}\hbar \omega} \nonumber \\[5pt] &= \sqrt{(2n + 1) \dfrac{\hbar}{m\omega}}. \nonumber \end{align} \nonumber \]
الأهمية
مع زيادة الرقم الكمي n، تزداد طاقة المذبذب وبالتالي سعة التذبذب (لتردد زاوي طبيعي ثابت). بالنسبة للرقم n الكبير، تتناسب السعة تقريبًا مع الجذر التربيعي للرقم الكمومي.
تظهر العديد من الميزات المثيرة للاهتمام في هذا الحل. على عكس المذبذب الكلاسيكي، يمكن أن تحتوي الطاقات المقاسة لمذبذب الكم على قيم الطاقة فقط المعطاة بالمعادلة\ ref {7.56}. علاوة على ذلك، على عكس حالة الجسيم الكمومي في الصندوق، تكون مستويات الطاقة المسموح بها متباعدة بالتساوي،
\[\begin{align} \Delta E &= E_{n+1} - E_n \\[5pt] &= \dfrac{2(n + 1) + 1}{2} \hbar \omega - \dfrac{2n + 1}{2} \hbar \omega \\[5pt] &= \hbar \omega = hf. \label{7.58} \end{align} \]
عندما ينتقل جسيم مرتبط بمثل هذا النظام من حالة الطاقة العالية إلى حالة الطاقة المنخفضة، فإن كمية الطاقة الأصغر التي يحملها الفوتون المنبعث هي بالضرورة\(hf\). وبالمثل، عندما ينتقل الجسيم من حالة الطاقة المنخفضة إلى حالة الطاقة العالية، يكون مقدار الطاقة الأصغر الذي يمكن أن يمتصه الجسيم هو\(hf\). يمكن لمذبذب الكم أن يمتص أو ينبعث الطاقة فقط بمضاعفات هذا الكم الأصغر من الطاقة. وهذا يتفق مع فرضية بلانك لتبادل الطاقة بين الإشعاع وجدران التجويف في مشكلة إشعاع الجسم الأسود.
يتكون الجزيء\(\ce{HCl}\) ثنائي الذرة من ذرة كلور واحدة وذرة هيدروجين واحدة. نظرًا لأن ذرة الكلور أكبر بـ 35 مرة من ذرة الهيدروجين، يمكن تقريب اهتزازات\(\ce{HCl}\) الجزيء جيدًا من خلال افتراض أن ذرة Cl بلا حركة وأن ذرة H تقوم بتذبذبات متناسقة بسبب القوة الجزيئية المرنة التي صممها قانون هوك. يحتوي الطيف الاهتزازي بالأشعة تحت الحمراء الذي تم قياسه لكلوريد الهيدروجين على أقل خط تردد يتركز عند\(f = 8.88 \times 10^{13} Hz\). ما المسافة بين الطاقات الاهتزازية لهذا الجزيء؟ ما ثابت القوة k للرابطة الذرية في جزيء HCl؟
إستراتيجية
يتوافق خط التردد الأدنى مع انبعاث الفوتونات ذات التردد الأدنى. تنبعث هذه الفوتونات عندما ينتقل الجزيء بين مستويين من الطاقة الاهتزازية المتجاورة. بافتراض أن مستويات الطاقة متباعدة بالتساوي، نستخدم Equation\ ref {7.58} لتقدير المسافات. يتم تقريب الجزيء جيدًا من خلال معالجة ذرة Cl على أنها ثقيلة للغاية وذرة H ككتلة\(m\) تؤدي التذبذبات. عند معالجة هذا النظام الجزيئي كمذبذب كلاسيكي، يتم العثور على ثابت القوة من العلاقة الكلاسيكية\(k = m\omega^2\).
الحل
تباعد الطاقة هو
\[ \begin{align} \Delta E &= hf \nonumber \\[5pt] &= (4.14 \times 10^{-15} eV \cdot s)(8.88 \times 10^{13} Hz) \nonumber\\[5pt] &= 0.368 \, eV. \nonumber \end{align} \nonumber \]
ثابت القوة هو
\[ \begin{align} k &= m \omega^2 \nonumber \\[5pt] &= m (2\pi f)^2 \nonumber \\[5pt] &= (1.67 \times 10^{ −27} kg)(2\pi \times 8.88 \times 10 ^{13}Hz)^2 \nonumber \\[5pt] &= 520 \, N/m. \nonumber \end{align} \nonumber \]
الأهمية
القوة بين الذرات في جزيء HCl قوية بشكل مدهش. الطاقة النموذجية المنبعثة في انتقالات الطاقة بين مستويات الاهتزاز هي في نطاق الأشعة تحت الحمراء. كما سنرى لاحقًا، غالبًا ما تصاحب التحولات بين مستويات الطاقة الاهتزازية لجزيء ثنائي الذرة التحولات بين مستويات الطاقة الدورانية.
التردد الاهتزازي لجزيء يوديد الهيدروجين HI هو\(6.69×10^{ 13}\,Hz\).
- ما ثابت قوة الرابطة الجزيئية بين ذرات الهيدروجين وذرات اليود؟
- ما طاقة الفوتون المنبعث عندما ينتقل هذا الجزيء بين مستويات الطاقة الاهتزازية المتجاورة؟
- الإجابة أ
-
295 نيوتن/متر
- الإجابة ب
-
0.277 فولت
يختلف المذبذب الكمي عن المذبذب الكلاسيكي بثلاث طرق:
- أولاً، الحالة الأرضية لمذبذب الكم ليست\(E_0 = \hbar \omega /2\) صفرًا. في العرض الكلاسيكي، أقل طاقة هي صفر. يعد عدم وجود حالة الطاقة الصفرية أمرًا شائعًا في جميع الأنظمة الميكانيكية الكمومية بسبب التقلبات المنتشرة في كل مكان والتي هي نتيجة لمبدأ عدم اليقين في Heisenberg. إذا جلس جسيم كمي بلا حراك في قاع البئر المحتمل، فسيتعين أن يكون زخمه وموقعه دقيقين في نفس الوقت، الأمر الذي من شأنه أن ينتهك مبدأ عدم اليقين لهايزنبرغ. لذلك، يجب أن تتميز حالة الطاقة المنخفضة بعدم اليقين في الزخم والموضع، لذلك يجب أن تقع الحالة الأرضية للجسيم الكمومي فوق قاع البئر المحتمل.
- ثانيًا، يمكن العثور على جسيم في جهد مذبذب توافقي كمي باحتمالية غير صفرية خارج الفاصل الزمني\(-A \leq x \leq +A\). في الصيغة الكلاسيكية للمشكلة، لن يكون للجسيم أي طاقة ليكون في هذه المنطقة. تبلغ احتمالية العثور على جسيم كمي من الحالة الأرضية في المنطقة المحرمة تقليديًا حوالي 16٪.
- ثالثًا، تكون توزيعات الكثافة الاحتمالية\(|\psi_n(x)|^2\) لمذبذب كمي في حالة الطاقة الأرضية المنخفضة\(\psi_0(x)\)، هي الأكبر في منتصف البئر\((x = 0)\). لكي يتم العثور على الجسيم بأكبر احتمال في مركز البئر، نتوقع أن يقضي الجسيم معظم الوقت هناك أثناء تذبذبه. هذا عكس سلوك المذبذب الكلاسيكي، حيث يقضي الجسيم معظم وقته في التحرك بسرعات صغيرة نسبيًا بالقرب من نقاط الدوران.
أوجد قيمة التوقع لموضع الجسم في الحالة الأرضية للمذبذب التوافقي باستخدام التماثل.
- الإجابة ب
-
\[\langle x \rangle = 0 \nonumber \]
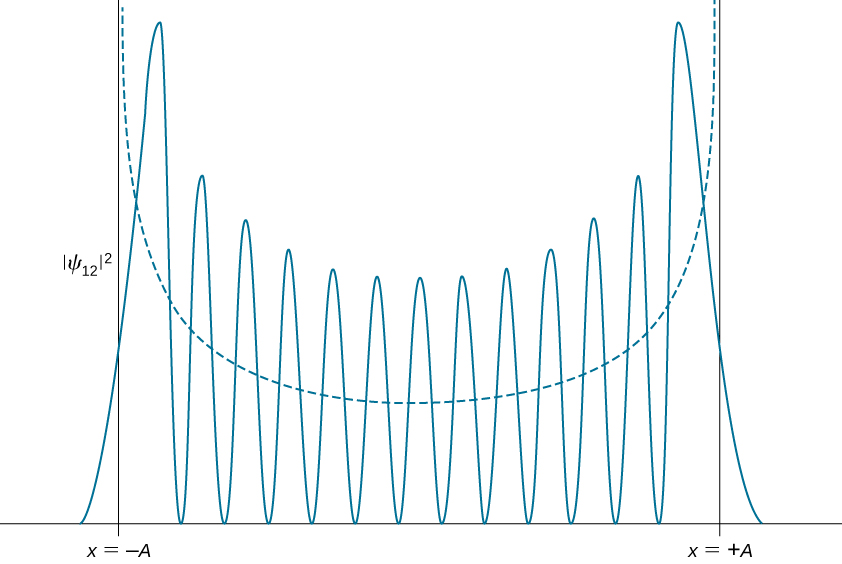
تتغير توزيعات الكثافة الاحتمالية الكمومية في الشخصية للحالات المثيرة، وتصبح أشبه بالتوزيع الكلاسيكي عندما يرتفع الرقم الكمي. نلاحظ هذا التغيير بالفعل في الحالة المثيرة الأولى لمذبذب كمي لأن التوزيع\(|\psi_1(x)|^ 2\) يبلغ ذروته حول نقاط التحول ويختفي عند موضع التوازن، كما هو موضح في الشكل\(\PageIndex{2}\). وفقًا لمبدأ المراسلات في بوهر، في حدود الأعداد الكمومية العالية، يتقارب الوصف الكمي للمذبذب التوافقي مع الوصف الكلاسيكي، الموضح في الشكل\(\PageIndex{3}\). إن توزيع كثافة الاحتمالية الكلاسيكي المقابل للطاقة الكمومية\(n = 12\) للحالة هو تقريب جيد بشكل معقول لتوزيع الاحتمال الكمي لمذبذب الكم في هذه الحالة المثيرة. تصبح هذه الاتفاقية أفضل بشكل متزايد للدول المتحمسة للغاية.