7.5: الجسيم الكمومي في صندوق
- Page ID
- 196788
في نهاية هذا القسم، ستكون قادرًا على:
- وصف كيفية إعداد مشكلة القيمة الحدية لمعادلة Schrdinger الثابتة
- اشرح سبب قياس طاقة الجسيم الكمومي في الصندوق
- وصف المعنى المادي للحلول الثابتة لمعادلة Schrdinger وربط هذه الحلول بالحالات الكمومية المعتمدة على الوقت
- شرح المعنى المادي لمبدأ المراسلات في Bohr
في هذا القسم، نطبق معادلة Schrdinger على جسيم مرتبط بصندوق أحادي البعد. توفر هذه الحالة الخاصة دروسًا لفهم ميكانيكا الكم في الأنظمة الأكثر تعقيدًا. يتم تحديد طاقة الجسيم كنتيجة لحالة الموجة الدائمة داخل الصندوق.
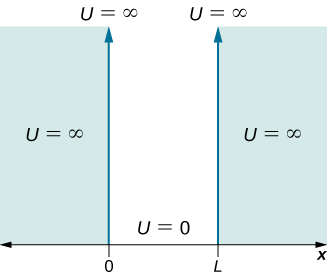
ضع في اعتبارك جسيمًا من الكتلة\(m\) يُسمح له بالتحرك فقط على طول الاتجاه x وتقتصر حركته على المنطقة الواقعة بين الجدران الصلبة والصلبة الموجودة عند\(x = 0\) وعند\(x = L\) (الشكل\(\PageIndex{1}\)). بين الجدران، يتحرك الجسيم بحرية. يُطلق على هذا الوضع المادي اسم البئر المربع اللانهائي، والذي يتم وصفه بواسطة وظيفة الطاقة الكامنة
\ [U (x) =\ ابدأ {الحالات}
0 و 0\ leq x\ leq\ leq L
\\ infty & x< 0\; and\; x> L\ end {الحالات}\ التسمية {3.5.2}\]
يؤدي الجمع بين هذه المعادلة مع معادلة الموجة المستقلة عن الوقت لـ Schrdinger إلى نتيجة
\[\dfrac{-\hbar^2}{2m} \dfrac{d^2\psi(x)}{dx^2} = E\psi(x), \, for \, 0 \leq x \leq L \label{7.32} \]
\(E\)أين الطاقة الكلية للجسيم. ما أنواع الحلول التي نتوقعها؟ طاقة الجسيم هي رقم موجب، لذلك إذا كانت قيمة دالة الموجة موجبة (الجانب الأيمن من المعادلة)، فإن انحناء دالة الموجة يكون سالبًا أو مقعرًا لأسفل (الجانب الأيسر من المعادلة). وبالمثل، إذا كانت قيمة دالة الموجة سالبة (الجانب الأيمن من المعادلة)، فإن انحناء دالة الموجة يكون موجبًا أو مقعرًا لأعلى (الجانب الأيسر من المعادلة). تتحقق هذه الحالة من خلال وظيفة الموجة المتذبذبة، مثل الموجة الجيبية أو موجة جيب التمام. نظرًا لأن هذه الموجات تقتصر على الصندوق، فإننا نتخيل موجات واقفة بنقاط نهاية ثابتة عند\(x = 0\) و\(x = L\).
\(\psi(x)\)حلول هذه المعادلة لها تفسير احتمالي. على وجه الخصوص،\(|\psi(x)|^2\) يمثل المربع الكثافة الاحتمالية لإيجاد الجسيم في موقع معين x. يجب دمج هذه الوظيفة لتحديد احتمال العثور على الجسيم في بعض فترات الفضاء. لذلك نحن نبحث عن حل قابل للتطبيع يلبي شرط التطبيع التالي:
\[\int_0^L dx|\psi(x)|^2 = 1. \label{7.33} \]
الجدران صلبة وغير قابلة للاختراق، مما يعني أن الجسيم لا يوجد أبدًا خارج الجدار. من الناحية الرياضية، هذا يعني أن الحل يجب أن يختفي عند الجدران:
\[\psi(0) = \psi(L) = 0. \label{7.34} \]
نتوقع حلولًا متذبذبة، لذا فإن الحل الأكثر عمومية لهذه المعادلة هو
\[\psi_k(x) = A_k \, \cos \, kx + B_k \, \sin \, kx \label{7.35} \]
\(k\)أين رقم الموجة،\(B_k\) وهي الثوابت.\(A_k\) يعطي تطبيق شرط الحدود المعبر عنه بالمعادلة\ ref {7.33}
\[\psi_k(0) = A_k \, \cos (k \cdot 0) + B_k \, \sin (k \cdot 0) = A_k = 0. \label{7.36} \]
لأن لدينا\(A_k = 0\)، يجب أن يكون الحل
\[\psi_k(x) = B_k \, \sin \, kx. \label{7.37} \]
إذا كان\(B_k\) صفرًا، فلا\(\psi_k(x) = 0\) يمكن تلبية جميع القيم\(x\) وشرط التطبيع (المعادلة\ ref {7.33}). بافتراض\(B_k \neq 0\) أن المعادلة\ المرجع {7.34}\(x = L\) بعد ذلك تعطي
\[0 = B_k \, \sin (kL) \Rightarrow \sin(kL) = 0 \Rightarrow kL = n\pi, \, n = 1,2,3,... \label{7.38} \]
نتجاهل\(n = 0\) الحل لأن\(\psi(x)\) هذا الرقم الكمي سيكون صفرًا في كل مكان - وهو حل غير قابل للتطبيع وبالتالي غير فيزيائي. يعطي استبدال المعادلة\ المرجع {7.37} بالمعادلة\ المرجع {7.32}
\[-\dfrac{\hbar^2}{2m}\dfrac{d^2}{dx^2} (B_k \sin(kx)) = E(B_k \sin(kx)). \label{7.39} \]
يؤدي حساب هذه المشتقات إلى
\[E = E_k = \dfrac{\hbar^2k^2}{2m}. \label{7.40} \]
وفقًا لـ de Broglie\(p = \hbar k\)، فإن هذا التعبير يعني أن الطاقة الكلية تساوي الطاقة الحركية، بما يتفق مع افتراضنا بأن «الجسيم يتحرك بحرية». الجمع بين نتائج المعادلة\ ref {7.38} و\ ref {7.40} يعطي
\[E_n = n^2 \dfrac{\pi^2 \hbar^2}{2mL^2}, \, n = 1,2,3,... \label{7.41} \]
تشير المعادلة\ ref {7.41} إلى أن الجسيم المرتبط بصندوق أحادي البعد يمكن أن يحتوي فقط على قيم منفصلة (كمية) للطاقة. علاوة على ذلك، لا يمكن للجسيم أن يحتوي على طاقة حركية صفرية - فمن المستحيل أن يكون الجسيم المرتبط بصندوق «في حالة سكون».
لتقييم وظائف الموجة المسموح بها التي تتوافق مع هذه الطاقات، يجب أن نجد ثابت التطبيع\(B_n\). نحن نفرض معادلة شرط التطبيع\ ref {7.33} على دالة الموجة
\[\psi_n(x) = B_n \, \sin \, \dfrac{n\pi x}{L} \label{7.42} \]
نبدأ بشرط التطبيع (المعادلة\ ref {7.33})
\[\begin{align} 1 &= \int_0^L dx|\psi_n(x)|^2 \\[5pt] &= \int_0^L dx \, B_n^2 \, \sin^2 \dfrac{n\pi}{L} x \\[5pt] &= B^2 n \int_0^2 dx \, \sin^2 \dfrac{n\pi}{L}x \\[5pt] &= B_n^2 \dfrac{L}{2} \\[5pt] \Rightarrow B_n &= \sqrt{\dfrac{2}{L}}. \end{align} \nonumber \]
وبالتالي، فإن وظائف الموجة التي تتوافق مع قيم الطاقة الواردة في المعادلة\ ref {7.41} هي
\[\psi_n(x) = \sqrt{\dfrac{2}{L}} \, \sin \, \dfrac{n\pi x}{L}, \, n = 1,2,3,... \label{7.43} \]
للحصول على أدنى حالة للطاقة أو طاقة الحالة الأرضية، لدينا
\[E_1 = \dfrac{\pi^2 \hbar^2}{2mL^2}, \, \psi_1(x) = \sqrt{\dfrac{2}{L}} \, \sin \left(\dfrac{\pi x}{L}\right). \label{7.44} \]
يمكن التعبير عن جميع حالات الطاقة الأخرى على النحو التالي
\[E_n = n^2 E_1, \, \psi_n(x) = \sqrt{\dfrac{2}{L}} \, \sin \, \left(\dfrac{n\pi x}{L}\right). \label{7.45} \]
\(n\)يسمى المؤشر بالرقم الكمي للطاقة أو الرقم الكمي الأساسي. الدولة\(n = 2\) هي أول ولاية متحمسة، والدولة\(n = 3\) هي الولاية الثانية المثيرة، وما إلى ذلك. يوضح الشكل الحالات الكمومية الثلاث الأولى (لـ n = 1 و2 و3) للجسيم في الصندوق\(\PageIndex{2}\). يشار أحيانًا إلى وظائف الموجة في المعادلة\ ref {7.45} باسم «حالات الطاقة المحددة». ويقال أن الجسيمات في هذه الحالات تحتل مستويات الطاقة، والتي تمثلها الخطوط الأفقية في الشكل\(\PageIndex{2}\). تتشابه مستويات الطاقة مع درجات السلم التي يمكن للجسيم أن «يتسلقها» عندما يكتسب الطاقة أو يفقدها.
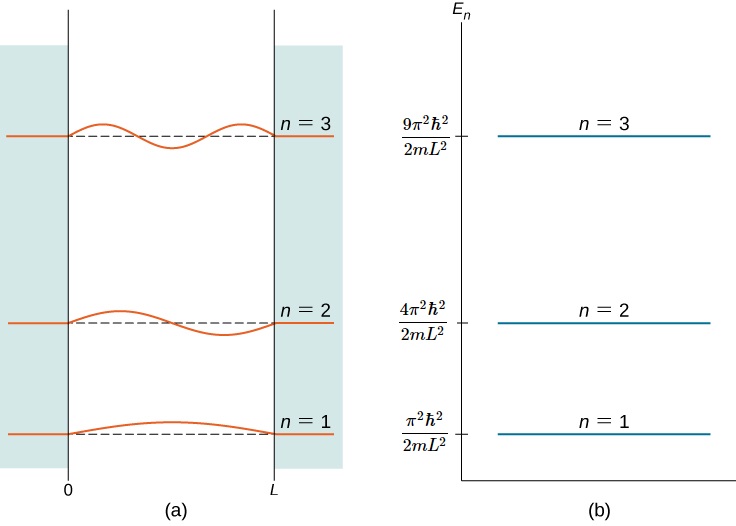
تسمى وظائف الموجة في المعادلة\ ref {7.45} أيضًا الحالات الثابتة وحالات الموجة الدائمة. هذه الوظائف «ثابتة»، لأن وظائف الكثافة الاحتمالية الخاصة بها\(|\Psi(x,t)|^2\)، لا تختلف في الوقت، و «الموجات الواقفة» لأن أجزائها الحقيقية والخيالية تتأرجح صعودًا وهبوطًا مثل الموجة الواقفة - مثل حبل يلوح بين طفلين في الملعب. الحالات الثابتة هي حالات الطاقة المحددة (المعادلة\ ref {7.45})، ولكن التوليفات الخطية لهذه الحالات، مثل\(\psi(x) = a\psi_1 + b\psi_2\) (أيضًا حلول معادلة Schrdinger) هي حالات الطاقة المختلطة.
تحديد كمية الطاقة هو نتيجة لظروف الحدود. إذا لم يقتصر الجسيم على صندوق ولكنه يتجول بحرية، فإن الطاقات المسموح بها تكون مستمرة. ومع ذلك، في هذه الحالة، يُسمح فقط ببعض الطاقات (\(E_1, 4E_1, 9E_1,...\)). يتم تحديد فرق الطاقة بين مستويات الطاقة المجاورة بواسطة
\[\Delta E_{n+1,n} = E_{n+1} - E_n = (n + 1)^2 E_1 - n^2E_1 = (2n + 1) E_1. \nonumber \]
يتطلب الحفاظ على الطاقة أنه في حالة تغير طاقة النظام، يتم نقل فرق الطاقة في شكل آخر من أشكال الطاقة. بالنسبة للحالة الخاصة للجسيم المشحون المحصور في حجم صغير (على سبيل المثال، في الذرة)، غالبًا ما يتم تغيير الطاقة بواسطة الفوتونات. توفر لنا ترددات الفوتونات المنبعثة معلومات حول اختلافات الطاقة (المسافات) للنظام وحجم الاحتواء - حجم «الصندوق» (المعادلة\ ref {7.44}).
لنفترض أن البروتون يقتصر على صندوق عرض\(L = 1.00 \times 10^{-14} m\) (نصف قطر نووي نموذجي). ما هي طاقات الأرض والدول المتحمسة الأولى؟ إذا انتقل البروتون من حالة الإثارة الأولى إلى الحالة الأرضية، فما طاقة الفوتون المنبعث وتردده؟
إستراتيجية
إذا افترضنا أن البروتون المحصور في النواة يمكن تشكيله كجسيم كمي في صندوق، فكل ما نحتاج إليه هو استخدام Equation\ ref {7.41} للعثور على طاقاته\(E_1\) و\(E_2\). كتلة البروتون هي\(m = 1.76 \times 10^{-27}kg\). يزيل الفوتون المنبعث فرق الطاقة\(\Delta E = E_2 - E_1\). يمكننا استخدام العلاقة\(E_f = hf\) لإيجاد ترددها f.
الحل
الحالة الأرضية:
\[\begin{align*} E_1 &= \dfrac{\pi^2 \hbar^2}{2mL^2} \\[5pt] &= \dfrac{\pi^2 (1.05 \times 10^{-34} J \cdot s)}{2(1.67 \times 10^{-27} kg)(1.00 \times 10^{-14}m)^2} \\[5pt] &= 3.28 \times 10^{−13}J \\[5pt] &= 2.05 \, MeV \end{align*} \nonumber \]
أول حالة متحمسة:
\[E_2 = 2^2 E_1 = 4(2.05 \, MeV) = 8.20 \, MeV. \nonumber \]
طاقة الفوتون المنبعث هي
\[E_f = \Delta E = E_2 - E_1 = 8.20 \, MeV - 2.05 \, MeV = 6.15 \, MeV. \nonumber \]
تردد الفوتون المنبعث هو
\[f = \dfrac{E_f}{h} = \dfrac{6.15 \, MeV}{4.14 \times 10^{-21}MeV \cdot s} = 1.49 \times 10^{21} Hz. \nonumber \]
الدلالة
هذا هو التردد النموذجي لأشعة جاما المنبعثة من النواة. تبلغ طاقة هذا الفوتون حوالي 10 ملايين مرة أكبر من طاقة فوتون الضوء المرئي.
تُعطى القيمة المتوقعة لموضع الجسيم في الصندوق بواسطة
\[\langle x \rangle = \int_0^L dx \,\psi_n^* (x) x \psi_n(x) = \int_0^L dx\,x|\psi_n^*(x)|^2 = \int_0^L dx\,x \dfrac{2}{L}sin^2 \, \dfrac{nπx}{L} = \dfrac{L}{2}. \label{7.47} \]
يمكننا أيضًا العثور على القيمة المتوقعة للزخم أو متوسط الزخم لعدد كبير من الجسيمات في حالة معينة:
\[\begin{align} \langle p \rangle &= \int_0^L dx\psi_n^* (x) \left[-i\hbar \dfrac{d}{dx} \psi_n(x)\right] \label{7.48} \\[5pt] &= -i\hbar \int_0^L dx \sqrt{\dfrac{2}{L}} \, \sin \, \dfrac{n\pi x}{L} \left[ \dfrac{d}{dx} \sqrt{\dfrac{2}{L}} \, \sin \, \dfrac{n\pi x}{L}\right] \\[5pt] &= -i \dfrac{2\hbar}{L} \int_0^L dx \, \sin \, \dfrac{n\pi x}{L} \left[ \dfrac{n\pi}{L} \, \cos \, \dfrac{n\pi x}{L}\right] \\[5pt] &= - i\dfrac{2n\pi \hbar}{L^2} \int_0^L dx \dfrac{1}{2} \sin \, \dfrac{2n\pi x}{L} \\[5pt] &= -i \dfrac{n\pi \hbar}{L^2} \dfrac{L}{2n\pi} \int_0^{2\pi n} d\varphi \, \sin \, \varphi \\[5pt] &= -i \dfrac{\hbar}{2L} \cdot 0 \\[5pt] &= 0. \end{align} \]
وبالتالي، بالنسبة لجسيم في حالة طاقة محددة، يكون متوسط الموضع في منتصف الصندوق ومتوسط زخم الجسيم هو صفر - كما هو الحال أيضًا للجسيم الكلاسيكي. لاحظ أنه في حين أن الحد الأدنى من طاقة الجسيم الكلاسيكي يمكن أن يكون صفرًا (يمكن أن يكون الجسيم في حالة سكون في منتصف الصندوق)، فإن الحد الأدنى من طاقة الجسيم الكمومي هو غير صفري وتعطى بواسطة المعادلة\ ref {7.44}. متوسط طاقة الجسيمات في الحالة الكمية النونية - القيمة المتوقعة للطاقة - هو
\[E_n = \langle E \rangle = n^2 \dfrac{\pi^2 \hbar^2}{2m}. \label{7.49} \]
النتيجة ليست مفاجئة لأن حالة الموجة الدائمة هي حالة طاقة محددة. يجب أن يؤدي أي قياس للطاقة في هذا النظام إلى إرجاع قيمة مساوية لإحدى هذه الطاقات المسموح بها.
لن يكتمل تحليلنا للجسيم الكمومي في الصندوق دون مناقشة مبدأ المراسلات الخاص بـ Bohr. ينص هذا المبدأ على أنه بالنسبة للأعداد الكمومية الكبيرة، يجب أن تعطي قوانين فيزياء الكم نتائج مماثلة لقوانين الفيزياء الكلاسيكية. لتوضيح كيفية عمل هذا المبدأ للجسيم الكمومي في صندوق، نرسم توزيع الكثافة الاحتمالية
\[|\psi_n(x)|^2 = \dfrac{2}{L} sin^2 (n\pi x/L) \label{7.50} \]
للعثور على الجسيم حول الموقع\(x\) بين الجدران عندما يكون الجسيم في حالة كمية\(\psi_n\). \(\PageIndex{3}\)يوضح الشكل هذه التوزيعات الاحتمالية للحالة الأرضية والحالة المثيرة الأولى والحالة المثيرة للغاية التي تتوافق مع عدد كمي كبير. نرى من هذه المخططات أنه عندما يكون الجسيم الكمومي في الحالة الأرضية، فمن المرجح أن يتم العثور عليه في منتصف الصندوق، حيث يكون للتوزيع الاحتمالي أكبر قيمة. لا يكون الأمر كذلك عندما يكون الجسيم في الحالة المثارة الأولى لأن التوزيع الاحتمالي الآن له القيمة الصفرية في منتصف الصندوق، لذلك لا توجد فرصة للعثور على الجسيم هناك. عندما يكون الجسيم الكمومي في الحالة المثارة الأولى، يكون للتوزيع الاحتمالي قسمان، وأفضل فرصة للعثور على الجسيم تكون في مواقع قريبة من مواقع هذه الحدود القصوى. هذه الصورة الكمومية تختلف عن الصورة الكلاسيكية.
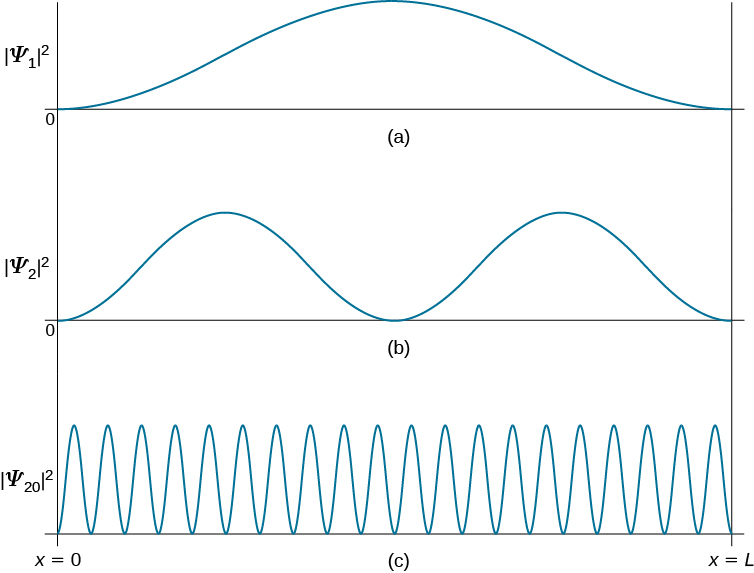
\(x + \Delta x\)تعتمد الكثافة الاحتمالية لإيجاد جسيم كلاسيكي\(x\) بين مقدار الوقت\(Δt\) الذي يقضيه الجسيم في هذه المنطقة. بافتراض أن سرعتها u ثابتة\(Δt = Δx/u\)، فإن هذه المرة ثابتة أيضًا لأي موقع بين الجدران. لذلك،\(x\) تكون الكثافة الاحتمالية لإيجاد الجسيم الكلاسيكي عند موحدة في جميع أنحاء الصندوق، ولا يوجد موقع مفضل للعثور على جسيم كلاسيكي. تتم مطابقة هذه الصورة الكلاسيكية في حدود الأعداد الكمومية الكبيرة. على سبيل المثال، عندما يكون الجسيم الكمومي في حالة شديدة الإثارة، كما هو موضح في الشكل\(\PageIndex{3}\)، تتميز الكثافة الاحتمالية بالتقلبات السريعة ومن ثم لا تعتمد احتمالية العثور على الجسيم الكمومي في الفاصل الزمني Δx على مكان وجود هذا الفاصل بين الجدران.
تتحرك عربة صغيرة تزن 0.40 كجم ذهابًا وإيابًا على طول مسار هوائي بين مصدين يقعان على بعد 2.0 متر. نحن نفترض عدم وجود احتكاك؛ فالتصادمات مع المصدات مرنة تمامًا بحيث تحافظ السيارة بين المصدات على سرعة ثابتة تبلغ 0.50 متر/ثانية، وعند التعامل مع العربة كجسيم كمي، قم بتقدير قيمة العدد الكمي الرئيسي الذي يتوافق مع طاقتها الكلاسيكية.
إستراتيجية
نجد الطاقة الحركية K للعربة وطاقة حالتها الأرضية\(E_1\) كما لو كانت جسيمًا كموميًا. طاقة العربة حركية بالكامل، لذلك\(K = n^2 E_1\) (المعادلة\ المرجع {7.45}). حل مشكلة ن يعطي\(n = (K/E_1)^{1/2}\).
الحل
الطاقة الحركية للعربة هي
\[K = \dfrac{1}{2} mu^2 = \dfrac{1}{2}(0.40 \, kg)(0.50 \, m/s)^2 = 0.050 \, J. \nonumber \]
الحالة الأرضية للعربة، التي تُعامل كجسيم كمي، هي
\[E_1 = \dfrac{\pi^2 \hbar^2}{2mL^2} = \dfrac{\pi^2 (1.05 \times 10^{-34} J \cdot s)^2}{2(0.40 \, kg)(2.0 \, m)^2} = 1.700 \times 10^{-68} J. \nonumber \]
لذلك،\[n = (K/E_1)^{1/2} = (0.050/1.700 \times 10^{-68})^{1/2} = 1.2 \times 10^{33}. \nonumber \]
الدلالة
نرى من هذا المثال أن طاقة النظام الكلاسيكي تتميز بعدد كمي كبير جدًا. يتعلق مبدأ مراسلات Bohr بهذا النوع من المواقف. يمكننا تطبيق شكلية ميكانيكا الكم على أي نوع من الأنظمة، الكمومية أو الكلاسيكية، والنتائج صحيحة في كل حالة. في حدود الأعداد الكمومية العالية، لا توجد ميزة في استخدام الشكلية الكمومية لأننا نستطيع الحصول على نفس النتائج باستخدام الشكليات الأقل تعقيدًا للميكانيكا الكلاسيكية. ومع ذلك، لا يمكننا تطبيق الشكلية الكلاسيكية على نظام كمي في حالة طاقة منخفضة العدد.
(أ) فكر في بئر مربع لا نهائي مع حدود الجدار\(x=0\) و\(x=L\). ما احتمال العثور على جسيم كمي في حالته الأرضية في مكان ما بين\(x=0\) و\(x=L/4\)؟ (ب) كرر السؤال (أ) للجسيم الكلاسيكي.
الحل
أ. 9.1%؛ ب. 25%
بعد العثور على الحالات الثابتة\(ψ_n(x)\) والطاقات\(E_n\) من خلال حل معادلة Schrdinger المستقلة عن الوقت (المعادلة\ ref {7.32})، نستخدم المعادلة 7.4.12 لكتابة دوال الموجة\(Ψ_n(x,t)\) التي تمثل حلولًا لمعادلة Schrdinger المعتمدة على الوقت والمعطاة بواسطة المعادلة 7.4.7. بالنسبة للجسيم الموجود في صندوق، يعطي هذا
\[\Psi_n(x,t) = e^{-i\omega_nt} \psi_n(x) = \sqrt{\dfrac{2}{L}}e^{-iE_nt/\hbar}sin \, \dfrac{n\pi x}{L}, \, n = 1,2,3,... \label{7.51} \]
حيث يتم إعطاء الطاقات بواسطة المعادلة\ ref {7.41}.
للجسيم الكمومي في النموذج الصندوقي تطبيقات عملية في مجال الإلكترونيات الضوئية الناشئ حديثًا نسبيًا، والذي يتعامل مع الأجهزة التي تحول الإشارات الكهربائية إلى إشارات بصرية. يتعامل هذا النموذج أيضًا مع الظواهر الفيزيائية النانوية، مثل الجسيمات النانوية المحاصرة في جهد كهربائي منخفض تحدها حواجز ذات إمكانات عالية.


