7.3: مبدأ عدم اليقين لهايزنبرغ
- Page ID
- 196765
في نهاية هذا القسم، ستكون قادرًا على:
- وصف المعنى المادي لعلاقة عدم اليقين بين الموضع والزخم
- شرح أصول مبدأ عدم اليقين في نظرية الكم
- وصف المعنى المادي لعلاقة عدم اليقين بين الطاقة والوقت
مبدأ عدم اليقين لهايزنبرغ هو مبدأ أساسي في ميكانيكا الكم. تقريبًا، تنص على أنه إذا عرفنا كل شيء عن مكان وجود الجسيم (عدم اليقين في الموضع صغير)، فإننا لا نعرف شيئًا عن زخمه (عدم اليقين في الزخم كبير)، والعكس صحيح. توجد أيضًا إصدارات من مبدأ عدم اليقين للكميات الأخرى أيضًا، مثل الطاقة والوقت. نناقش مبادئ وضع الزخم وعدم اليقين في وقت الطاقة بشكل منفصل.
الزخم والموضع
لتوضيح مبدأ عدم اليقين في موضع الزخم، ضع في اعتبارك الجسيم الحر الذي يتحرك على طول الاتجاه x. يتحرك الجسيم بسرعة\(u\) وزخم ثابتين\(p = mu\). وفقًا لعلاقات دي برولي,\(p = \hbar k\) و\(E = \hbar \omega\). كما تمت مناقشته في القسم السابق، يتم إعطاء وظيفة الموجة للجسيم الحر بواسطة
\[ \begin{align*} \psi_k(x,t) &= A[\cos \, (\omega t - kx) - i \, \sin \, (\omega t - kx)] \\[4pt] &= A \, e^{-i(\omega t - kx)} \\[4pt] &= A \, e^{-i(\omega t - kx)} \\[4pt] &=A\, e^{-i\omega t} e^{ikx} \end{align*} \nonumber \]
وكثافة\(|\psi_k (x,t)|^2 = A^2\) الاحتمالات موحدة ومستقلة عن الوقت. من المحتمل أيضًا العثور على الجسيم في أي مكان على طول المحور x ولكن له قيم محددة لطول الموجة ورقم الموجة، وبالتالي الزخم. إن عدم اليقين في الموقف غير محدود (نحن غير متأكدين تمامًا من الموقف) وعدم اليقين بشأن الزخم هو صفر (نحن متأكدون تمامًا من الزخم). يتوافق هذا الحساب للجسيم الحر مع مبدأ عدم اليقين لهايزنبرغ.
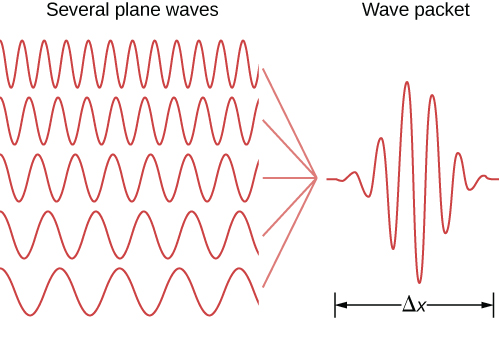
يمكن إجراء بيانات مماثلة من الجسيمات الموضعية. في نظرية الكم، يتم نمذجة الجسيم الموضعي من خلال التراكب الخطي لحالات الجسيمات الحرة (أو الموجة المستوية) التي تسمى حزمة الموجة. يظهر مثال لحزمة الموجة في الشكل\(\PageIndex{1}\). تحتوي الحزمة الموجية على العديد من الأطوال الموجية، وبالتالي من خلال علاقات de Broglie، فإن العديد من اللحظات - ممكنة في ميكانيكا الكم! يحتوي هذا الجسيم أيضًا على العديد من قيم الموضع، على الرغم من أن الجسيم يقتصر في الغالب على الفاصل الزمني\(\Delta x\). يمكن تحديد موضع الجسيم بشكل أفضل (\(\Delta x\)يمكن تقليله) إذا تمت إضافة المزيد من حالات الموجات المستوية ذات الأطوال الموجية المختلفة أو اللحظات معًا بالطريقة الصحيحة (\(\Delta p\)تمت زيادتها). وفقًا لهايزنبرغ، فإن هذه الشكوك تخضع للعلاقة التالية.
لا يمكن أبدًا أن يكون ناتج عدم اليقين في موضع الجسيم وعدم اليقين في زخمه أقل من نصف ثابت بلانك المخفض:
\[\Delta x \Delta p \geq \dfrac{\hbar}{2}. \label{Heisen} \]
تعبر هذه العلاقة عن مبدأ عدم اليقين لهايزنبرغ. يضع قيودًا على ما يمكننا معرفته عن الجسيم من القياسات المتزامنة للموضع والزخم. \(\Delta x\)إنها كبيرة وصغيرة\(\Delta p\) والعكس صحيح. يمكن اشتقاق المعادلة\ ref {Heisen} في دورة أكثر تقدمًا في الفيزياء الحديثة. وبالتأمل في هذه العلاقة في عمله «المبادئ الفيزيائية لنظرية الكم»، كتب هايزنبرغ «أي استخدام لكلمتي 'الموضع' و 'السرعة' بدقة تتجاوز تلك التي توفرها [العلاقة] لا معنى له تمامًا مثل استخدام الكلمات التي لم يتم تعريف معناها».
لاحظ أن مبدأ عدم اليقين لا علاقة له بدقة الجهاز التجريبي. حتى بالنسبة لأجهزة القياس المثالية، ستظل أوجه عدم اليقين هذه قائمة لأنها تنشأ في طبيعة المادة الشبيهة بالموجة. \(\Delta x \Delta p\)تعتمد القيمة الدقيقة للمنتج على الشكل المحدد لوظيفة الموجة. ومن المثير للاهتمام أن الدالة الغوسية (أو توزيع منحنى الجرس) تعطي الحد الأدنى لقيمة منتج عدم اليقين:
\[\Delta x \Delta p = \dfrac{\hbar}{2} \nonumber \]
حدد الحد الأدنى من حالات عدم اليقين في مواضع الأشياء التالية إذا كانت سرعاتها معروفة بدقة تبلغ\(1.0 \times 10^{-3} m/s\):
- إلكترون و
- كرة بولينج كتلتها 6.0 كجم.
إستراتيجية
نظرًا لعدم اليقين في السرعة\(\Delta u = 1.0 \times 10^{-3} m/s\)، يتعين علينا أولاً تحديد عدم اليقين في الزخم\(\Delta p = m\Delta u\) ثم عكس المعادلة\ ref {Heisen} للعثور على عدم اليقين في الموضع
\[\Delta x = \dfrac{\hbar}{2\Delta p}. \nonumber \]
الحل
- بالنسبة للإلكترون:\[\begin{align*} \Delta p &= m\Delta u \\[4pt] &= (9.1 \times 10^{-31} kg)(1.0 \times 10^{-3}m/s) \\[4pt] &= 9.1 \times 10^{-34} kg \cdot m/s,\end{align*} \nonumber \]\[\begin{align*} \Delta x &= \frac{\hbar}{2\Delta p} \\[4pt] &= 5.8 \, cm. \end{align*} \nonumber \]
- بالنسبة إلى كرة البولينج:\[\begin{align*} \Delta p &= m\Delta u \\[4pt] &= (6.0 \, kg)(1.0 \times 10^{-3}m/s) \\[4pt] &= 6.0 \times 10^{-3} kg \cdot m/s, \end{align*} \nonumber \]\[\begin{align*} \Delta x &= \frac{\hbar}{2\Delta p} \\[4pt] &= 8.8 \times 10^{-33}m. \end{align*} \nonumber \]
الأهمية
على عكس عدم اليقين في موضع الإلكترون، فإن عدم اليقين في موضع كرة البولينج صغير للغاية. ثابت بلانك صغير جدًا، لذا فإن القيود التي يفرضها مبدأ عدم اليقين ليست ملحوظة في الأنظمة العيانية مثل كرة البولينج.
قم بتقدير طاقة الحالة الأرضية لذرة الهيدروجين باستخدام مبدأ عدم اليقين لهايزنبرغ. (تلميح: وفقًا للتجارب المبكرة، يبلغ حجم ذرة الهيدروجين حوالي 0.1 نانومتر.)
إستراتيجية
يمكن نمذجة الإلكترون المرتبط بذرة الهيدروجين بجسيم مرتبط بصندوق أحادي البعد طوله\(L = 0.1 \, nm\). وظيفة موجة الحالة الأرضية لهذا النظام هي نصف موجة. هذا هو أكبر طول موجي يمكن أن «يتناسب» مع الصندوق، لذا فإن وظيفة الموجة تتوافق مع أدنى حالة طاقة. لاحظ أن هذه الدالة تشبه إلى حد كبير دالة Gaussian (منحنى الجرس). يمكننا أخذ متوسط طاقة الجسيم الموصوف بهذه الوظيفة (E) كتقدير جيد لطاقة الحالة الأرضية (\(E_0\)). يرتبط متوسط طاقة الجسيم بمتوسط مربع الزخم، والذي يرتبط بعدم اليقين في زخمه.
الحل
لحل هذه المشكلة، يجب أن نكون محددين بشأن المقصود بـ «عدم اليقين في الموقف» و «عدم اليقين في الزخم». نحدد عدم اليقين في الموضع (Δx) مع الانحراف المعياري للموضع (\(σ_x\))، وعدم اليقين في الزخم (\(Δp\)) مع الانحراف المعياري للزخم (\(σ_p\)). بالنسبة للوظيفة الغوسية، فإن منتج عدم اليقين هو
\[\sigma_x\sigma_p = \frac{\hbar}{2}, \nonumber \]
حيث
\[\sigma_x^2 = x^2 - \overline{x}^2 \nonumber \]
و
\[\sigma_p^2 = p^2 - \overline{p}^2.\nonumber \]
من المرجح أن يتحرك الجسيم يسارًا بنفس القدر الذي يتحرك فيه اليمين، لذلك\(\overline{p}^2 = 0\). كما أن عدم اليقين في الموضع يمكن مقارنته بحجم الصندوق، لذلك\(\sigma_x = L\). وبالتالي فإن طاقة الحالة الأرضية المقدرة هي
\[\begin{align*} E_0 &= E_{Gaussian} \\[4pt] &= \dfrac{\overline{p}^2}{m} \\[4pt] &= \frac{\sigma_p^2}{2m} \\[4pt] &= \frac{1}{2m} \left(\frac{\hbar}{2\sigma_x}\right)^2 \\[4pt] &= \frac{1}{2m} \left(\frac{\hbar}{2L}\right)^2 \\[4pt] &= \frac{\hbar^2}{8mL^2}. \end{align*} \nonumber \]
\[\begin{align*}E_0 &= \dfrac{(\hbar c)^2}{8(mc^2)L^2} \\[4pt] &= \frac{(197.3 \, eV \cdot nm)^2}{8(0.511 \cdot 10^6 eV)(0.1 \, nm)^2} \\[4pt] &= 0.952 \, eV \approx 1 \, eV. \end{align*} \nonumber \]
ضرب البسط والمقام\(c^2\) بالعطاء
الأهمية
استنادًا إلى التقديرات المبكرة لحجم ذرة الهيدروجين ومبدأ عدم اليقين، فإن طاقة الحالة الأرضية لذرة الهيدروجين تقع في نطاق eV. تبلغ طاقة التأين للإلكترون في طاقة الحالة الأرضية حوالي 10 eV، لذلك تم تأكيد هذا التنبؤ تقريبًا. (ملاحظة: غالبًا ما يكون المنتج cc قيمة مفيدة في إجراء العمليات الحسابية في ميكانيكا الكم.)
الطاقة والوقت
هناك نوع آخر من مبدأ عدم اليقين يتعلق بأوجه عدم اليقين في القياسات المتزامنة لطاقة الحالة الكمومية وعمرها،
\[\Delta E \Delta t \geq \frac{\hbar}{2} \label{H2} \]
\(\Delta E\)أين عدم اليقين في قياس الطاقة وعدم اليقين في قياس العمر.\(\Delta t\) لا ينتج مبدأ عدم اليقين في وقت الطاقة عن علاقة من النوع الذي تعبر عنه المعادلة\ ref {Heisen} لأسباب فنية تتجاوز هذه المناقشة. ومع ذلك، فإن المعنى العام لمبدأ وقت الطاقة هو أن الحالة الكمومية الموجودة لفترة قصيرة فقط لا يمكن أن تحتوي على طاقة محددة. والسبب هو أن تردد الحالة يتناسب عكسياً مع الوقت وأن التردد يتصل بطاقة الحالة، لذلك لقياس الطاقة بدقة جيدة، يجب ملاحظة الحالة للعديد من الدورات.
للتوضيح، ضع في اعتبارك الحالات المثيرة للذرة. يمكن استنتاج الأعمار المحدودة لهذه الحالات من أشكال الخطوط الطيفية التي لوحظت في أطياف الانبعاثات الذرية. في كل مرة تتحلل فيها حالة الإثارة، تختلف الطاقة المنبعثة قليلاً، وبالتالي، يتميز خط الانبعاثات بتوزيع الترددات الطيفية (أو الأطوال الموجية) للفوتونات المنبعثة. ونتيجة لذلك، تتميز جميع الخطوط الطيفية بعرض طيفي. يتوافق متوسط طاقة الفوتون المنبعث مع الطاقة النظرية للحالة المثارة ويعطي الموقع الطيفي لقمة خط الانبعاث. تتمتع الحالات قصيرة العمر بعرض طيفي واسع والحالات طويلة العمر لها عرض طيفي ضيق.
عادة ما توجد الذرة في حالة حماسية لمدة تقارب\(\Delta t = 10^{-8} s\). قم بتقدير عدم اليقين\(\Delta f\) في تردد الفوتونات المنبعثة عندما تنتقل الذرة من حالة الإثارة بالانبعاث المتزامن للفوتون بمتوسط تردد يبلغ\(f = 7.1 \times 10^{14} Hz\). هل الإشعاع المنبعث أحادي اللون؟
إستراتيجية
نقوم بعكس المعادلة\ ref {H2} للحصول على عدم اليقين في الطاقة\(\Delta E \approx \hbar /2\Delta t\) ودمجها مع طاقة الفوتون\(E = hf\) للحصول عليها\(\Delta f\). لتقدير ما إذا كان الانبعاث أحادي اللون أم لا، نقوم بالتقييم\(\Delta f/f\).
الحل
الانتشار في طاقات الفوتون هو\(\Delta E = h \Delta f\). لذلك،
\[\Delta E \approx \frac{\hbar}{2 \Delta t} \Rightarrow h \Delta t \approx \frac{\hbar}{2 \Delta t} \Rightarrow \Delta f \approx \frac{1}{4\pi \Delta t} = \frac{1}{4\pi (10^{-8}s)} = 8.0 \times 10^6 \, Hz, \nonumber \]
\[\frac{\Delta f}{f} = \frac{8.0 \times 10^6 \, Hz}{7.1 \times 10^{14} \, Hz} = 1.1 \times 10^{-8}. \nonumber \]
الأهمية
نظرًا لأن الفوتونات المنبعثة لها تردداتها في حدود\(1.1 \times 10^{-6}\) نسبة مئوية من متوسط التردد، يمكن اعتبار الإشعاع المنبعث أحادي اللون.
تنتقل ذرة الصوديوم من الحالة المثارة الأولى إلى الحالة الأرضية، حيث تنبعث منها فوتون 589.0 نانومتر بطاقة 2.105 eV. إذا كان عمر هذه الحالة المثيرة هو\(1.6 \times 10^{-8} s\)، فما هو عدم اليقين في طاقة هذه الحالة المثيرة؟ ما عرض الخط الطيفي المقابل؟
- إجابة
-
\(4.1 \times 10^{-8} eV\)؛\(1.1 \times 10^{-5} nm\)


