Skip to main content
Global

5.9: الزخم النسبي

  1. Last updated
  2. Save as PDF
  • Page ID
    196697

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • تعريف الزخم النسبي من حيث الكتلة والسرعة
    • أظهر مدى ارتباط الزخم النسبي بالزخم الكلاسيكي
    • أظهر كيف يؤدي الحفاظ على الزخم النسبي إلى تقييد الأجسام ذات الكتلة بسرعات أقل من c

    الزخم هو مفهوم مركزي في الفيزياء. تم تحديد الشكل الأوسع لقانون نيوتن الثاني من حيث الزخم. يتم الحفاظ على الزخم عندما تكون القوة الخارجية الصافية على النظام صفرًا. وهذا يجعل الحفاظ على الزخم أداة أساسية لتحليل التصادمات (الشكل\(\PageIndex{1}\)). يأتي الكثير مما نعرفه عن البنية دون الذرية من تحليل تصادمات الجسيمات النسبية المنتجة بواسطة المسرع، ويلعب الحفاظ على الزخم دورًا مهمًا في هذا التحليل.

    صورة لاعب كرة قدم يتصدى لخصم.
    الشكل\(\PageIndex{1}\): الزخم هو مفهوم مهم للاعبي كرة القدم هؤلاء من جامعة كاليفورنيا في بيركلي وجامعة كاليفورنيا في ديفيس. يصطدم لاعب بنفس السرعة ولكن بكتلة أكبر بتأثير أكبر لأن زخمه أكبر. بالنسبة للأجسام التي تتحرك بسرعات نسبية، يكون التأثير أكبر.

    تنص الفرضية الأولى للنسبية على أن قوانين الفيزياء هي نفسها في جميع الإطارات بالقصور الذاتي. هل يصمد قانون الحفاظ على الزخم على هذا المطلب بسرعات عالية؟ يمكن إثبات أن الزخم المحسوب على أنه مجرد\(\vec{p} = m\frac{d\vec{x}}{dt}\)، حتى لو تم حفظه في إطار مرجعي واحد، قد لا يتم حفظه في إطار مرجعي آخر بعد تطبيق تحويل لورنتز على السرعات. بدلاً من ذلك، يمكن إظهار المعادلة الصحيحة للزخم على أنها التعبير الكلاسيكي بدلالة الزيادة dللوقت المناسب للجسيم، والذي لوحظ في إطار راحة الجسيم:

    \[\begin{align*} \vec{p} &= m\frac{d\vec{x}}{dτ} = m\frac{d\vec{x}}{dt} \frac{dt}{d\tau} \\[5pt] &= m\frac{d\vec{x}}{dt}\frac{1}{\sqrt{1 - u^2/c^2}} \\[5pt] &= \frac{m\vec{u}}{\sqrt{1 - u^2/c^2}} \\[5pt] &= \gamma m\vec{u}.\end{align*} \nonumber \]

    تعريف: الزخم النسبي وكتلة الراحة

    الزخم النسبي\(\vec{p}\) هو الزخم الكلاسيكي مضروبًا في العامل النسبي\(\gamma\):

    \[\vec{p} = \gamma m\vec{u} \label{Rmomentum} \]

    أين\(m\) كتلة بقية الجسم،\(\vec{u}\) هي سرعته بالنسبة للراصد،\(γ\) وهو العامل النسبي:

    \[\gamma = \frac{1}{\sqrt{1 - \frac{u^2}{c^2}}}. \label{Rmass} \]

    لاحظ أننا نستخدم السرعة هنا\(u\) لتمييزها عن السرعة النسبية\(v\) بين المراقبين. العامل\(\gamma\) الذي يحدث هنا له نفس شكل العامل النسبي السابق\(\gamma\) باستثناء أنه الآن من حيث سرعة الجسيم\(u\) بدلاً من السرعة النسبية v لإطارين مرجعيين.

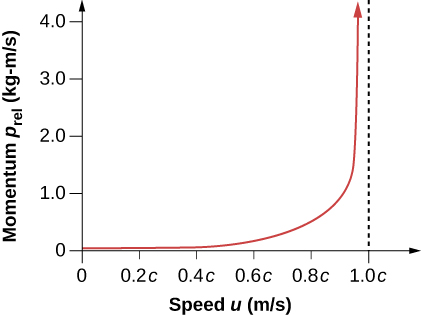
    مع التعبير عن p بهذه الطريقة،\(p_{tot}\) يتم الحفاظ على الزخم الكلي عندما تكون القوة الخارجية الصافية صفرًا، تمامًا كما هو الحال في الفيزياء الكلاسيكية. مرة أخرى نرى أن الكمية النسبية تصبح تقريبًا نفس الكمية الكلاسيكية بسرعات منخفضة، حيث\(u/c\) تكون صغيرة\(\gamma\) وتساوي تقريبًا 1. الزخم النسبي له نفس الدور البديهي للزخم الكلاسيكي. وهي أكبر بالنسبة للكتل الكبيرة التي تتحرك بسرعات عالية، ولكن بسبب العامل\(\gamma\)، يقترب الزخم النسبي من اللانهاية مع\(u\) اقتراب\(c\) (الشكل\(\PageIndex{2}\)). هذا مؤشر آخر على أن الجسم ذو الكتلة لا يمكنه الوصول إلى سرعة الضوء. وإذا حدث ذلك، فإن زخمها سيصبح بلا حدود - وهي قيمة غير معقولة.

    هذا رسم بياني للزخم النسبي كدالة للسرعة. تكون الدالة ومنحدرها صفرًا عند u=0، وكلاهما يزداد مع u، ويكون للدالة خط تقارب رأسي عند u=1.0 c
    الشكل\(\PageIndex{2}\): يقترب الزخم النسبي من اللانهاية مع اقتراب سرعة الجسم من سرعة الضوء.
    الكتلة مقابل كتلة الراحة

    أحيانًا ما يُفهم التعريف الصحيح نسبيًا للزخم (المعادلة\ ref {Rmomentum}) على أنه يشير إلى أن الكتلة تختلف مع السرعة:\(m_{var} = \gamma m\)، خاصة في الكتب المدرسية القديمة. ومع ذلك، لاحظ\(m\) أن كتلة الجسم تقاسها شخص في حالة سكون بالنسبة للجسم. وبالتالي،\(m\) يتم تعريفها على أنها كتلة الراحة، والتي يمكن قياسها عند الراحة، ربما باستخدام الجاذبية. عندما تتحرك الكتلة بالنسبة إلى الراصد، فإن الطريقة الوحيدة لتحديد كتلتها هي من خلال التصادمات أو الوسائل الأخرى التي تتضمن الزخم. نظرًا لأن كتلة الجسم المتحرك لا يمكن تحديدها بشكل مستقل عن الزخم، فإن الكتلة الوحيدة ذات المعنى هي كتلة الراحة. لذلك، عندما نستخدم مصطلح «الكتلة»، افترض أنه مطابق لـ «كتلة الراحة».

    يتم تعريف الزخم النسبي بطريقة تحافظ على الزخم في جميع الأطر بالقصور الذاتي. عندما تكون القوة الخارجية الصافية على النظام صفرًا، يتم الحفاظ على الزخم النسبي، تمامًا كما هو الحال بالنسبة للزخم الكلاسيكي. تم التحقق من ذلك في العديد من التجارب.

    التمارين\(\PageIndex{1}\)

    ما مقدار حركة الإلكترون الذي يتحرك بسرعة\(0.985c\)؟ الكتلة الباقية للإلكترون هي\(9.11 \times 10^{-31} kg\).

    إجابة

    استبدل البيانات بالمعادلة\ ref {Rmomentum}:

    \[\begin{align*} p &= \gamma mu \\[5pt] &= \frac{mu}{\sqrt{1 - \frac{u^2}{c^2}}} \\[5pt] &= \frac{(9.11 \times 10^{-31}kg)(0.985)(3.00 \times 10^8 \, m/s)}{\sqrt{1 - \frac{(0.985c)^2}{c^2}}} \\[5pt] &= 1.56 \times 10^{-21} \, kg-m/s. \end{align*} \nonumber \]