5.8: تأثير دوبلر للضوء

Last updated
Save as PDF

Page ID: 196683

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

اشرح أصل التحول في التردد والطول الموجي للطول الموجي المرصود عندما يتحرك الراصد والمصدر نحو أو بعيدًا عن بعضهما البعض
اشتقاق تعبيرًا عن تحول دوبلر النسبي
قم بتطبيق معادلات تحول دوبلر على أمثلة العالم الحقيقي

كما تمت مناقشته في الفصل الخاص بالصوت، إذا كان مصدر الصوت والمستمع يتحركان بعيدًا عن بعضهما البعض، فإن المستمع يواجه عددًا أقل من دورات الموجة في كل ثانية، وبالتالي تردد أقل، مما لو ظل الفصل بينهما ثابتًا. وللسبب نفسه، يكتشف المستمع ترددًا أعلى إذا كان المصدر والمستمع يقتربان. يحدث تحول دوبلر الناتج في التردد المكتشف لأي شكل من أشكال الموجات. ومع ذلك، بالنسبة للموجات الصوتية، تختلف معادلات تحول دوبلر بشكل ملحوظ اعتمادًا على ما إذا كان المصدر أو الراصد أو الهواء هو الذي يتحرك. لا يتطلب الضوء أي وسيط، ويعتمد تحول دوبلر للضوء الذي ينتقل في الفراغ فقط على السرعة النسبية للمراقب والمصدر.

تأثير دوبلر النسبي

لنفترض أن\(S\) الراصد يرى الضوء من مصدر\(S'\) يتحرك بعيدًا بسرعة\(v\) (الشكل\(\PageIndex{1}\)). يمكن قياس الطول الموجي للضوء في غضون\(S'\) - على سبيل المثال، باستخدام مرآة لإعداد موجات قائمة وقياس المسافة بين العقد. هذه المسافات هي الأطوال المناسبة\(S'\) كإطار الراحة الخاص بها، وتتغير بعامل\(\sqrt{1 - v^2/c^2}\) عند قياسها في إطار الراصد\(S\)، حيث يُنظر إلى المسطرة التي تقيس الطول الموجي فيها\(S'\) على أنها تتحرك.

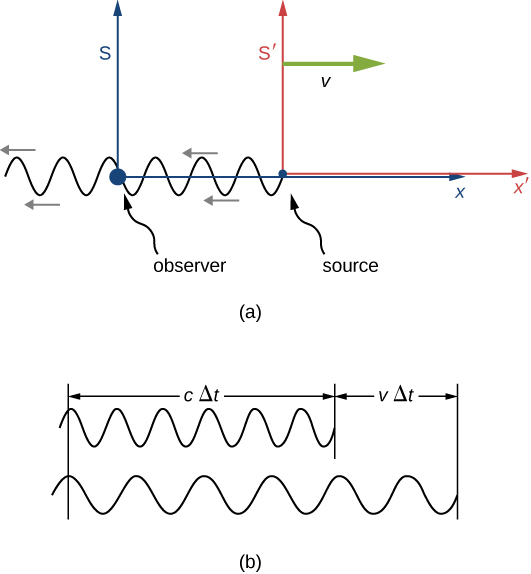
في الشكل أ: يظهر الراصد عند أصل إطار ثابت S. يتحرك الإطار الرئيسي S إلى اليمين بسرعة v بالنسبة للإطار S. يظهر مصدر في أصل S prime ينبعث منه موجة جيبية تنتشر إلى اليسار. في الشكل ب، تظهر ست دورات للموجة كما يراها الراصد وكما يراها المصدر. الطول الموجي للموجة التي يراها الراصد أطول من الموجة التي يراها المصدر. تمت تسمية عرض الدورات الست كما يراها المصدر بـ c delta t. الطول الإضافي حتى نهاية الدورات الست كما يراه الراصد يسمى v delta t. — الشكل\(\PageIndex{1}\): (أ) عندما تنبعث موجة ضوئية من مصدر ثابت في إطار القصور الذاتي المتحرك S'، يرى الراصد في S أن الطول الموجي المقاس بـ S. يكون أقصر بعامل\(\sqrt{1 - v^2/c^2}\). (ب) نظرًا لأن الراصد يرى المصدر يتحرك بعيدًا داخل S، فإن نمط الموجة الذي يصل إلى الراصد في S يتمدد أيضًا بفعل العامل\((c\Delta t + v\Delta t)/(c\Delta t) = 1 + v/c\).

إذا كان المصدر ثابتًا في S، فسيشاهد الراصد طول CΔt لنمط الموجة في الوقت Δt. ولكن بسبب حركة S بالنسبة إلى S، والتي تعتبر فقط داخل S، يرى الراصد نمط الموجة، وبالتالي الطول الموجي، ممتدًا بعامل

\[\frac{c\Delta t_{period} + v\Delta t_{period}}{c\Delta t_{period}} = 1 + \frac{v}{c} \nonumber \]

كما هو موضح في (ب) من الشكل\(\PageIndex{1}\). تعطي الزيادة الإجمالية من كلا التأثيرين

\[\begin{align*} \lambda_{obs} &= \lambda_{src} \left(1 + \frac{v}{c}\right) \sqrt{\frac{1}{1 - \frac{v^2}{c^2}}} \\[4pt] &= \lambda_{src} \left(1 + \frac{v}{c}\right) \sqrt{\frac{1}{\left(1 + \frac{v}{c}\right) \left(1 - \frac{v}{c}\right)}} \\[4pt] &= \lambda_{src}\sqrt{\frac{\left(1 + \frac{v}{c}\right)}{\left(1 - \frac{v}{c}\right)}} \end{align*} \nonumber \]

\(\lambda_{src}\)أين الطول الموجي للضوء الذي يراه المصدر في S\(\lambda_{obs}\) وهو الطول الموجي الذي يكتشفه الراصد داخل S.

التحولات الحمراء والتحولات الزرقاء

الطول الموجي\(λ_{obs}\) المرصود للإشعاع الكهرومغناطيسي أطول (يسمى «التحول الأحمر») من ذلك المنبعث من المصدر عندما يتحرك المصدر بعيدًا عن الراصد. وبالمثل، يكون الطول الموجي أقصر (يسمى «التحول الأزرق») عندما يتحرك المصدر نحو الراصد. يتم تحديد مقدار التغيير من خلال

\[\lambda_{obs} = \lambda_s \sqrt{\frac{\left(1 + \frac{v}{c}\right)}{\left(1 - \frac{v}{c}\right)}} \nonumber \]

\(\lambda_s\)أين الطول الموجي في الإطار المرجعي للمصدر،\(v\) وهي السرعة النسبية للإطارين\(S\) و\(S'\). السرعة\(v\) موجبة للحركة بعيدًا عن الراصد وسلبية للحركة تجاه الراصد. من حيث تردد المصدر والتردد الملحوظ، يمكن كتابة هذه المعادلة على النحو التالي:

\[ f_{obs} = f_s \sqrt{\frac{\left(1 - \frac{v}{c}\right)}{\left(1 + \frac{v}{c}\right)}} \label{eq20} \]

لاحظ أن العلامات تختلف عن تلك الموجودة في معادلة الطول الموجي.

مثال\(\PageIndex{1}\): Calculating a Doppler Shift

لنفترض أن المجرة تتحرك بعيدًا عن الأرض بسرعة 0.825 درجة مئوية. تنبعث منه موجات راديو بطول موجة يبلغ

0.525 م. ما الطول الموجي الذي سنكتشفه على الأرض؟

إستراتيجية

نظرًا لأن المجرة تتحرك بسرعة نسبية، يجب علينا تحديد تحول دوبلر لموجات الراديو باستخدام تحول دوبلر النسبي بدلاً من تحول دوبلر الكلاسيكي.

الحل

التعرف على الأشياء المعروفة:\(u = 0.825 c\)؛\(\lambda_s = 0.525 \, m\).
حدد المجهول:\(\lambda_{obs}\).
عبِّر عن الإجابة في صورة معادلة:
\[\lambda_{obs} = \lambda_s \sqrt{\frac{1 + \frac{v}{c}}{1 - \frac{v}{c}}}. \nonumber \]
قم بالحساب:
\[\begin{align*}\lambda_{obs} &= \lambda_s \sqrt{\frac{1 + \frac{v}{c}}{1 - \frac{v}{c}}} \\[4pt] &= (0.525 \, m) \sqrt{\frac{1 + \frac{0.825c}{c}}{1 - \frac{0.825c}{c}}} \\[4pt] &= 1.70 \, m. \end{align*} \nonumber \]

الأهمية

نظرًا لأن المجرة تبتعد عن الأرض، فإننا نتوقع أن تتحول الأطوال الموجية للإشعاع الذي تنبعث منه إلى اللون الأحمر. الطول الموجي الذي قمنا بحسابه هو 1.70 m، وهو محمر من الطول الموجي الأصلي البالغ 0.525 م، وستلاحظ في فيزياء الجسيمات وعلم الكونيات أن اكتشاف الإشعاع الأحمر أدى إلى فهم أصل الكون وتطوره في الوقت الحاضر.

التمارين الرياضية\(\PageIndex{1}\)

لنفترض أن المسبار الفضائي يتحرك بعيدًا عن الأرض بسرعة 0.350 c. يرسل رسالة موجات راديو إلى الأرض بتردد 1.50 جيجا هرتز. في أي تردد يتم استقبال الرسالة على الأرض؟

الحل

يمكننا استبدال البيانات مباشرة في المعادلة لتردد دوبلر النسبي (المعادلة\ ref {eq20}):

\[\begin{align*}f_{obs} &= f_s \sqrt{\frac{1 - \frac{v}{c}}{1 + \frac{v}{c}}} \\[4pt] &= (1.50 \, GHz)\sqrt{\frac{1 - \frac{0.350c}{c}}{1 + \frac{0.350c}{c}}} \\[4pt] &= 1.04 \, GHz. \end{align*} \nonumber \]

يحتوي تأثير دوبلر النسبي على تطبيقات تتراوح من مراقبة العاصفة برادار دوبلر إلى توفير معلومات عن حركة النجوم ومسافتها. وصفنا بعض هذه التطبيقات في التمارين.