Skip to main content
Global

5.7: تحويل السرعة النسبية

  1. Last updated
  2. Save as PDF
  • Page ID
    196685

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • اشتقاق المعادلات المتوافقة مع النسبية الخاصة لتحويل السرعات في إطار مرجعي بالقصور الذاتي إلى آخر.
    • قم بتطبيق معادلات تحويل السرعة على الأجسام التي تتحرك بسرعات نسبية.
    • افحص كيفية مقارنة السرعات المجمعة التي تنبأت بها معادلات التحويل النسبي مع تلك المتوقعة بشكل كلاسيكي.

    يتطلب البقاء في مكانه في قوارب الكاياك في نهر سريع الحركة جهدًا. يسحب تيار النهر قوارب الكاياك على طول الطريق. يمكن أن تؤدي محاولة التجديف عكس التدفق إلى تحريك قوارب الكاياك في اتجاه المنبع بالنسبة إلى الماء، ولكن هذا لا يمثل سوى جزء من سرعته بالنسبة للشاطئ. تعد حركة قوارب الكاياك مثالاً على كيفية دمج السرعات في ميكانيكا نيوتن عن طريق إضافة المتجهات. سرعة قوارب الكاياك هي المجموع المتجه لسرعته بالنسبة للماء وسرعة الماء بالنسبة إلى ضفة النهر. ومع ذلك، فإن الإضافة النسبية للسرعات مختلفة تمامًا.

    تحولات السرعة

    تخيل سيارة تسير ليلاً على طول طريق مستقيم، كما في الشكل\(\PageIndex{1}\). يرى السائق الضوء وهو يخرج من المصابيح الأمامية بسرعة\(c\) ضمن الإطار المرجعي للسيارة. إذا تم تطبيق التحول الجاليلي على الضوء، فإن الضوء المنبعث من المصابيح الأمامية للسيارة سيقترب من المشاة بسرعة\(u = v + c\)، على عكس افتراضات أينشتاين.

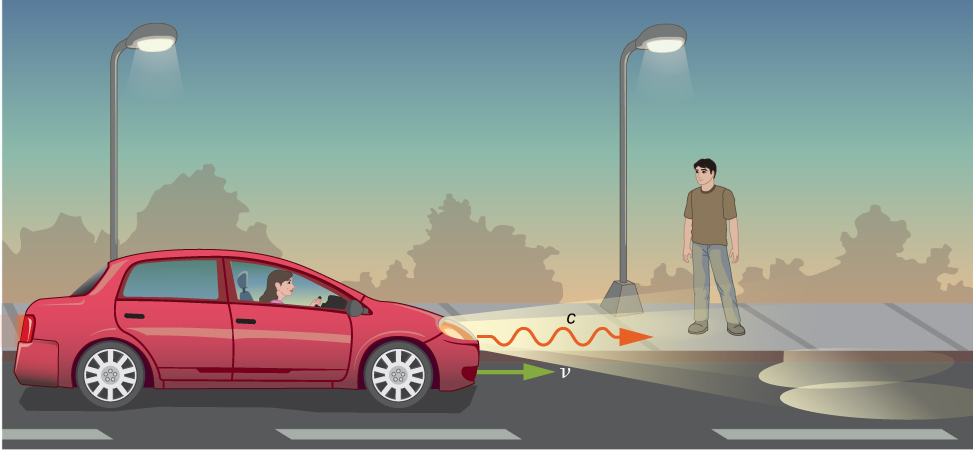
    رسم توضيحي لسيارة تتحرك بسرعة v، مع ضوء قادم من المصابيح الأمامية بسرعة أكبر c.
    الشكل\(\PageIndex{1}\): وفقًا للنتائج التجريبية والافتراض النسبي الثاني، يتحرك الضوء المنبعث من المصابيح الأمامية للسيارة بعيدًا عن السيارة بسرعة\(c\) باتجاه الراصد على الرصيف بسرعة\(c\).

    يختلف كل من المسافة المقطوعة ووقت السفر في الإطارين المرجعيين، ويجب أن يختلفا بطريقة تجعل سرعة الضوء هي نفسها في جميع الإطارات بالقصور الذاتي. يمكن الحصول على القواعد الصحيحة لتحويل السرعات من إطار إلى آخر من معادلات تحويل Lorentz.

    التحول النسبي للسرعة

    لنفترض أن الكائن P يتحرك بسرعة ثابتة\(u = (u'_x, u'_y, u'_z)\) كما تم قياسه في\(S'\) الإطار. يتحرك\(S'\) الإطار على طول محور x بسرعة\(v\). في زيادة الوقت dt '، يتم إزاحة الجسيم\(dx'\) على طول المحور x. يعطي تطبيق معادلات تحويل Lorentz الزيادات المقابلة للوقت والإزاحة في المحاور غير المجهزة:

    \[\begin{align} dt &= \gamma (dt' + vdx' /c^2) \\[4pt] dx &= \gamma (dx' + vdt') \\[4pt] dy &= dy' \\[4pt] dz &= dz'. \end{align} \nonumber \]

    يتم بعد ذلك تحديد مكونات السرعة للجسيم الذي يظهر في نظام الإحداثيات غير المطلي

    \[\begin{align} \dfrac{dx}{dt} &= \dfrac{\gamma(dx' + vdt')}{\gamma (dt' + v\,dx'/c^2)} = \dfrac{\dfrac{dx'}{dt'} + v}{1 + \dfrac{v}{c^2} \dfrac{dx'}{dt'}} \\[4pt] \dfrac{dy}{dt} &= \dfrac{dy'}{\gamma (dt' + v\,dx'/c^2)} = \dfrac{\dfrac{dy'}{dt'}}{\gamma \left(1 + \dfrac{v}{c^2} \dfrac{dx'}{dt'}\right)} \\[4pt] \dfrac{dz}{dt} &= \dfrac{dz'}{\gamma (dt' + v\,dx'/c^2)} = \dfrac{\dfrac{dz'}{dt'}}{\gamma \left(1 + \dfrac{v}{c^2} \dfrac{dx'}{dt'}\right)} \end{align} \nonumber \]

    وهكذا نحصل على معادلات مكونات السرعة للكائن كما هو موضح في الإطار\(S\):

    \[u_x = \left(\dfrac{u'_x + v}{1 + vu'_x/c^2}\right), \, u_y = \left(\dfrac{u'_y/\gamma}{1 + vu'_x/c^2}\right), \, u_z = \left(\dfrac{u'_z/\gamma}{1 + vu'_x/c^2}\right). \nonumber \]

    قارن هذا بالطريقة التي يقول بها التحول الجاليلي للميكانيكا الكلاسيكية أن السرعات تتغير، عن طريق الإضافة ببساطة كمتجهات:

    \[u_x = u'_x + u, \, u_y = u'_y, \, u_z = u'_z. \nonumber \]

    عندما تكون السرعة النسبية للإطارات أصغر بكثير من سرعة الضوء، أي عندما ينخفض\(v\gg c,\) قانون إضافة السرعة النسبية الخاصة إلى قانون سرعة غاليليو. عندما تكون سرعة\(v\)\(S'\) النسبة إلى\(S\) قابلة للمقارنة مع سرعة الضوء، يعطي قانون إضافة السرعة النسبية نتيجة أقل بكثير من إضافة السرعة الكلاسيكية (الجاليلية).

    مثال\(\PageIndex{1}\): Velocity Transformation Equations for Light

    لنفترض أن سفينة الفضاء تتجه مباشرة نحو الأرض بنصف سرعة الضوء ترسل إشارة إلينا على شعاع ضوء ينتج بالليزر (الشكل\(\PageIndex{2}\)). إذا كان الضوء يغادر السفينة\(c\) بالسرعة التي تُلاحظ من السفينة، فاحسب السرعة التي يقترب بها من الأرض.

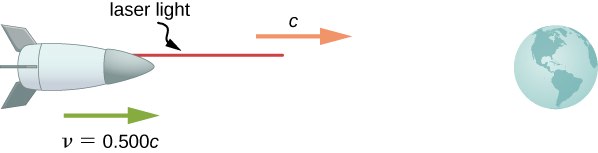
    رسم توضيحي لسفينة فضائية تتحرك إلى اليمين بسرعة v=0.500c وينبعث منها شعاع ليزر أفقي ينتشر إلى اليمين بسرعة c.
    الشكل\(\PageIndex{2}\): ما مدى سرعة اقتراب إشارة الضوء من الأرض إذا تم إرسالها من سفينة فضائية مسافرة\(0.500c\)؟

    إستراتيجية

    نظرًا لأن الضوء وسفينة الفضاء يتحركان بسرعات نسبية، لا يمكننا استخدام إضافة السرعة البسيطة. بدلاً من ذلك، نحدد السرعة التي يقترب بها الضوء من الأرض باستخدام إضافة السرعة النسبية.

    الحل

    التعرف على الأشياء المعروفة:\(v = 0.500c\)؛\(u' = c\).

    حدد المجهول:\(u\).

    عبِّر عن الإجابة في صورة معادلة:\(u = \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}}\).

    قم بالحساب:

    \[ \begin{align*} u &= \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}} \\[4pt] &= \dfrac{0.500c + c}{1 + \dfrac{(0.500c) (c)}{c^2}} \\[4pt] &= \dfrac{(0.500 + 1)c}{\left(\dfrac{c^2 + 0.500c^2}{c^2}\right)} = c. \end{align*} \nonumber \]

    الدلالة

    تعطي إضافة السرعة النسبية النتيجة الصحيحة. يخرج الضوء من السفينة بسرعة\(c\) ويقترب من الأرض بسرعة\(c\). سرعة الضوء مستقلة عن الحركة النسبية للمصدر والمراقب، سواء كان الراصد على متن السفينة أو على الأرض.

    لا يمكن أن تزيد السرعات عن سرعة الضوء، بشرط أن\(v\) تكون أقل من\(c\)\(u'\) ولا تتجاوز\(c\). يوضح المثال التالي أن إضافة السرعة النسبية ليست متماثلة مثل إضافة السرعة الكلاسيكية.

    مثال\(\PageIndex{2}\): Relativistic Package Delivery

    لنفترض أن سفينة الفضاء في المثال السابق تقترب من الأرض بنصف سرعة الضوء وتطلق علبة بسرعة\(0.750c\) (الشكل\(\PageIndex{3}\)).

    1. ما السرعة التي يرى بها الراصد الأرضي العلبة إذا تم إطلاقها مباشرة نحو الأرض؟
    2. إذا تم تصويره مباشرة بعيدًا عن الأرض؟
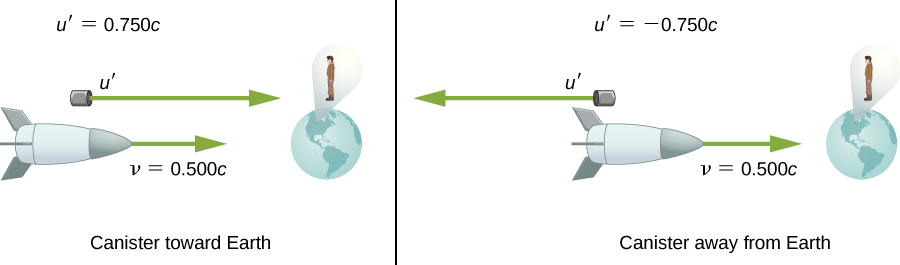
    يُظهر الرسم التوضيحي الأول سفينة الفضاء تتحرك إلى اليمين، نحو الأرض، بسرعة v=0.500c، وعلبة تتحرك إلى اليمين بسرعة u prime = 0.750c. يُظهر الرسم التوضيحي الثاني سفينة الفضاء تتحرك إلى اليمين، باتجاه الأرض، بسرعة v=0.500c، وعلبة تتحرك إلى اليسار بسرعة u prime = -0.750c.
    الشكل\(\PageIndex{3}\): يتم إطلاق علبة بسرعة 0.7500 درجة مئوية باتجاه الأرض أو بعيدًا عن الأرض.

    إستراتيجية

    نظرًا لأن العلبة وسفينة الفضاء تتحركان بسرعات نسبية، يجب أن نحدد سرعة العلبة بواسطة مراقب أرضي باستخدام إضافة السرعة النسبية بدلاً من إضافة السرعة البسيطة.

    حل لـ (أ)

    1. التعرف على الأشياء المعروفة:\(v = 0.500c\)؛\(u' = 0.750c\).
    2. حدد المجهول:\(u\).
    3. عبِّر عن الإجابة في صورة معادلة:\(u = \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}}\).
    4. قم بالحساب:\[\begin{align*} u &= \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}} \\[4pt] &= \dfrac{0.500c + 0.750c}{1 + \dfrac{(0.500c)(0.750c)}{c^2}} \\[4pt] &= 0.909c. \end{align*} \nonumber \]

    حل لـ (ب)

    1. التعرف على الأشياء المعروفة:\(v = 0.500c\)؛\(u' = - 0.750c\).
    2. حدد المجهول:\(u\).
    3. عبِّر عن الإجابة في صورة معادلة:\(u = \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}}\).
    4. قم بالحساب:\[\begin{align*} u &= \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}} \\[4pt] &= \dfrac{0.500c + (-0.750c)}{1 + \dfrac{(0.500c)(-0.750c)}{c^2}} \\[4pt] &=- 0.400c. \end{align*} \nonumber \]

    الدلالة

    تشير علامة الطرح إلى سرعة بعيدة عن الأرض (في الاتجاه المعاكس من\(v\))، مما يعني أن العلبة تتجه نحو الأرض في الجزء (أ) وبعيدًا في الجزء (ب)، كما هو متوقع. لكن السرعات النسبية لا تضيف ببساطة كما تفعل بشكل كلاسيكي. في الجزء (أ)، تقترب العلبة من الأرض بشكل أسرع، ولكن بأقل من مجموع المتجهات للسرعات، مما سيعطي\(1.250c\). في الجزء (ب)، تتحرك العلبة بعيدًا عن الأرض بسرعة −0.400 درجة مئوية، وهي أسرع من السرعة -0.250c المتوقعة بشكل كلاسيكي. الاختلافات في السرعات ليست متماثلة حتى: في الجزء (أ)، يرى راصد على الأرض العلبة والسفينة تتحركان بعيدًا بسرعة 0.409 درجة مئوية وبسرعة 0.900 درجة مئوية في الجزء (ب).

    التمارين\(\PageIndex{1}\)

    المسافات على طول الاتجاه العمودي على الحركة النسبية للإطارين هي نفسها في كلا الإطارين. لماذا إذن تختلف السرعات المتعامدة مع اتجاه x في الإطارين؟

    إجابة

    على الرغم من أن الإزاحات العمودية على الحركة النسبية هي نفسها في كلا الإطارين المرجعيين، فإن الفاصل الزمني بين الأحداث يختلف،\(dt\) والاختلافات\(dt'\) وتؤدي إلى سرعات مختلفة تظهر من الإطارين.