5.6: تحول لورنتز
- Page ID
- 196696
- وصف التحول الجاليلي للميكانيكا الكلاسيكية، وربط الموقع والوقت والسرعات والتسرعات المقاسة في إطارات مختلفة بالقصور الذاتي
- اشتق معادلات تحويل لورنتز المقابلة، والتي، على عكس التحول الجاليلي، تتوافق مع النسبية الخاصة
- اشرح تحول لورنتز والعديد من ميزات النسبية من حيث الزمكان رباعي الأبعاد
لقد استخدمنا افتراضات النسبية لفحص، على وجه الخصوص، كيف يقيس المراقبون في الأطر المرجعية المختلفة القيم المختلفة للأطوال والفواصل الزمنية. يمكننا الحصول على مزيد من الأفكار حول كيفية تغيير افتراضات النسبية للنظرة النيوتونية للزمان والمكان من خلال فحص معادلات التحويل التي تعطي إحداثيات المكان والزمان للأحداث في إطار مرجعي بالقصور الذاتي من حيث تلك الموجودة في آخر. ندرس أولاً كيفية تحول إحداثيات الموضع والوقت بين الإطارات بالقصور الذاتي وفقًا للعرض في الفيزياء النيوتونية. ثم ندرس كيف يجب تغيير ذلك للاتفاق مع افتراضات النسبية. أخيرًا، ندرس معادلات تحويل لورنتز الناتجة وبعض عواقبها من حيث مخططات الزمكان الأربعة الأبعاد، لدعم الرأي القائل بأن عواقب النسبية الخاصة تنتج عن خصائص الزمان والمكان نفسه، وليس الكهرومغناطيسية.
معادلات تحويل جاليليو
يتم تحديد الحدث من خلال موقعه ووقته\((x, y, z, t)\) بالنسبة لإطار مرجعي معين بالقصور الذاتي\(S\). على سبيل المثال،\((x, y, z, t)\) يمكن أن تشير إلى موضع الجسيم في الوقت المناسب\(t\)، ويمكن أن ننظر إلى هذه المواضع لعدة أوقات مختلفة لمتابعة حركة الجسيم. لنفترض أن الإطار المرجعي الثاني\(S'\) يتحرك بسرعة\(v\) فيما يتعلق بالأول. من أجل البساطة، افترض أن هذه السرعة النسبية تقع على طول المحور السيني. إذن العلاقة بين الوقت والإحداثيات في الإطارين المرجعيين هي
\[\begin{align} x &= x' + vt \label{eq1} \\[4pt] y &= y' \label{eq2} \\[4pt] x &= z'. \label{eq3} \end{align} \]
تتضمن هذه المعادلات الافتراض بأن قياسات الوقت التي أجراها المراقبون في كليهما\(S\)\(S'\) هي نفسها. وهذا هو،
\[t = t' \label{eq4} \]
تُعرف المعادلات\ ref {eq1} -\ ref {eq4} مجتمعة باسم تحويل غاليليو.
يمكننا الحصول على معادلات سرعة جاليليو وتحويل التسارع من خلال تمييز هذه المعادلات فيما يتعلق بالوقت. نستخدم\(u\) سرعة الجسيم في جميع أنحاء هذا الفصل لتمييزه عن\(v\) السرعة النسبية لإطارين مرجعيين. لاحظ أنه بالنسبة لتحويل غاليليو، فإن الزيادة في الوقت المستخدم في التفريق لحساب سرعة الجسيمات هي نفسها في كلا الإطارين\(dt = dt'\). عوائد التمايز
\[u_x = u'_x + v, \,u_y = u'_y, \,u_z = u'_z \nonumber \]
و
\[a_x = a'_x, \,a_y = a'_y, \,a_z = a'_z. \nonumber \]
نحن نشير إلى سرعة الجسيم\(u\) بدلاً\(v\) من تجنب الخلط مع سرعة\(v\) إطار مرجعي واحد فيما يتعلق بالآخر. تختلف السرعات في كل إطار حسب السرعة التي يراها إطار واحد من الإطار الآخر. يقيس المراقبون في كلا الإطارين المرجعيين نفس قيمة التسارع. نظرًا لأن الكتلة لا تتغير بالتحويل، والمسافات بين النقاط غير مشحونة، يرى المراقبون في كلا الإطارين نفس القوى\(F = ma\) المؤثرة بين الأجسام ونفس شكل قوانين نيوتن الثانية والثالثة في جميع الإطارات بالقصور الذاتي. تتوافق قوانين الميكانيكا مع الافتراض الأول للنسبية.
معادلات تحويل لورنتز
ومع ذلك، فإن التحول الجاليلي ينتهك افتراضات أينشتاين، لأن معادلات السرعة تنص على أن نبضة الضوء التي تتحرك بسرعة\(c\) على طول المحور x ستنتقل بسرعة\(c - v\) في إطار القصور الذاتي الآخر. على وجه التحديد، يكون للنبض الكروي نصف قطر\(t\) في\(r = ct\) الوقت المناسب في الإطار غير المطلي، وله أيضًا نصف قطر في\(r' = ct'\) الوقت t في الإطار المطلي. التعبير عن هذه العلاقات في الإحداثيات الديكارتية يعطي
\[ \begin{align} x^2 + y^2 + z^2 - c^2t^2 &= 0 \label{eq21} \\[4pt] x'^2 + y'^2 + z'^2 - c^2t'^2 &= 0. \label{eq22} \end{align} \]
يمكن ضبط معادلات الجانبين الأيسر\ ref {eq21} و\ ref {eq22} على قدم المساواة لأن كلاهما صفرًا. لأننا\(y = y'\)\(z = z'\) نحصل على
\[x^2 - c^2t^2 = x'^2 - c^2t'^2. \nonumber \]
لا يمكن تحقيق ذلك بالنسبة للسرعة\(v\) النسبية غير الصفرية للإطارين إذا افترضنا أن تحويل جاليليو ينتج\(t = t'\) مع\(x = x' + vt'\).
للعثور على المجموعة الصحيحة من معادلات التحويل، افترض نظامي الإحداثيات\(S\)\(S'\) وفي الشكل\(\PageIndex{1}\). افترض أولاً أن الحدث يقع\((x', 0, 0, t')\) في الداخل\(S'\) والخارج\((x, 0, 0, t)\)\(S\)، كما هو موضح في الشكل\(\PageIndex{1}\).
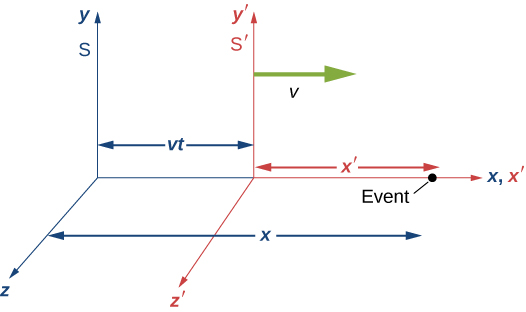
لنفترض أنه في اللحظة التي تتزامن فيها أصول أنظمة الإحداثيات في S و S، يصدر مصباح فلاش نبضة ضوئية منتشرة كرويًا بدءًا من الأصل. في الوقت t، يجد مراقب في S أن أصل S موجود\(x = vt\). بمساعدة صديق في S، يقيس مراقب S أيضًا المسافة من الحدث إلى أصل S ويجد ذلك\(x'\sqrt{1 - v^2/c^2}\). يأتي ذلك لأننا أظهرنا بالفعل افتراضات النسبية التي تشير إلى تقلص الطول. وبالتالي فإن موضع الحدث في S هو
\[x = vt + x'\sqrt{1 - v^2/c^2} \nonumber \]
و
\[x' = \dfrac{x - vt}{x'\sqrt{1 - v^2/c^2}}. \label{eq10} \]
تشير افتراضات النسبية إلى أن المعادلة المتعلقة بالمسافة والوقت لجبهة الموجة الكروية:
\[x^2 + y^2 + z^2 - c^2t^2 = 0 \nonumber \]
يجب تطبيقه من حيث الإحداثيات الأولية وغير المجهزة، والتي تم عرضها أعلاه لتؤدي إلى المعادلة:
\[x^2 - c^2t^2 = x'^2 - c^2t'^2. \nonumber \]
ندمج هذا مع المعادلة\ ref {eq10} التي\(x′\) تتعلق\(x\) وللحصول على العلاقة بين\(t\) و\(t'\):
\[t' = \dfrac{t - vx/c^2}{\sqrt{1 - v^2/c^2}}. \nonumber \]
المعادلات المتعلقة بوقت وموضع الأحداث كما هو موضح في\(S\) هي ثم
\[ \begin{align} t &= \dfrac{t' + vx'/c^2}{\sqrt{1 - v^2/c^2}}. \\[4pt] x &= \dfrac{x' + vt'}{\sqrt{1 - v^2/c^2}}. \\[4pt] y &= y' \\[4pt] z &= z'. \end {align} \nonumber \]
تُعرف هذه المجموعة من المعادلات، التي تربط الموضع والوقت في الإطارين بالقصور الذاتي، باسم تحويل لورنتز. وقد تم تسميتهم على شرف إتش إيه لورنتز (1853-1928)، الذي اقترحهم لأول مرة. ومن المثير للاهتمام أنه برر التحول على أساس ما تم اكتشافه في النهاية على أنه فرضية خاطئة. الأساس النظري الصحيح هو نظرية النسبية الخاصة لأينشتاين.
يعبر التحويل العكسي عن المتغيرات من حيث تلك الموجودة في S.\(S\) إن مجرد تبديل المتغيرات الأولية وغير الجاهزة والاستبدال يعطي:
\[\begin{align*} t'& = \dfrac{t - vx/c^2}{\sqrt{1 - v^2/c^2}} \\[4pt] x' &= \dfrac{x - vt}{\sqrt{1 - v^2/c^2}} \\[4pt] y' &= y \\[4pt] z' &= z. \end{align*} \nonumber \]
المركبة الفضائية S' في طريقها إلى Alpha Centauri عندما تمر بها المركبة الفضائية S بسرعة نسبية c /2. يرسل قبطان S إشارة راديو تدوم 1.2 ثانية وفقًا لساعة تلك السفينة. استخدم تحويل Lorentz للعثور على الفاصل الزمني للإشارة المقاسة بواسطة مسؤول الاتصالات في سفينة الفضاء S.
الحل
- حدد المعروف:\(\Delta t' = t'_2 - t'_1 = 1.2 s; \,\Delta x' = x'_2 - x'_1 = 0.\)
- حدد المجهول:\(\Delta t = t_2 - t_1\).
- عبِّر عن الإجابة في صورة معادلة. تبدأ إشارة الوقت كـ (\(x', t'_1\)) وتتوقف عند (\(x', t'_1\)). لاحظ أن إحداثيات x لكلا الحدثين هي نفسها لأن الساعة في حالة سكون في S. اكتب معادلة تحويل لورنتز الأولى بدلالة الإحداثيات الأولية\(\Delta t = t_2 - t_1\)\(\Delta x = x_2 - x_1\)، وبالمثل بالنسبة للإحداثيات الأولية، على النحو التالي:
\[\Delta t = \dfrac{\Delta t' + v\Delta x'/c^2}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]
نظرًا لأن موضع الساعة في S ثابت\(\Delta x' = 0\)،\(\Delta t\) ويصبح الفاصل الزمني:\[\Delta t = \dfrac{\Delta t'}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]
- قم بالحساب.
مع\(\Delta t' = 1.2 \,s\) هذا يعطي:
\[\begin{align*} \Delta t &= \dfrac{1.2 \,s}{\sqrt{1 - \left(\dfrac{1}{2}\right)^2}} \\[4pt] &= 1.6 \,s. \end{align*} \nonumber \]
لاحظ أن تحويل لورنتز يعيد إنتاج معادلة التمدد الزمني.
يقوم المساح بقياس الشارع ليكون\(L = 100 \,m\) طويلًا في إطار الأرض\(S\). استخدم تحويل لورنتز للحصول على تعبير عن طوله المقاس من سفينة فضائية\(S'\)، متحركًا بسرعة\(0.20c\)، بافتراض تطابق\(x\) إحداثيات الإطارين في الوقت المناسب\(t = 0\).
الحل
- تحديد المعروف:\(L = 100 \,m\)؛\(v = 0.20 c\)؛\(\Delta \tau = 0\).
- حدد المجهول:\(L'\).
- عبِّر عن الإجابة في صورة معادلة. قام المساح في الإطار S بقياس طرفي العصا في وقت واحد، ووجدهما في حالة راحة\(x_2\) وعلى\(x_1\) مسافة\(L = x_2 - x_1 = 100 \,m\) بعيدة. يقيس طاقم سفينة الفضاء الموقع المتزامن لأطراف العصي في إطارها. لربط الأطوال التي سجلها المراقبون في S وS، على التوالي، اكتب الثانية من معادلات تحويل لورنتز الأربعة على النحو التالي:
\[\begin{align*} x'_2 - x'_1 &= \dfrac{x_2 - vt}{\sqrt{1 - v^2/c^2}} - \dfrac{x_1 - vt}{\sqrt{1 - v^2/c^2}} \\[4pt] &= \dfrac{x_2 - x_2}{\sqrt{1 - v^2/c^2}} \\[4pt] &= \dfrac{L}{\sqrt{1 - v^2/c^2}}. \end{align*} \nonumber \]
- قم بالحساب. \(x_2 - x_1 = 100 \,m\)لأن طول العصا المتحركة يساوي:
\[\begin{align*} L' &= (100 \,m)\sqrt{1 - v^2/c^2} \\[4pt] &= (100 \,m)\sqrt{1 - (0.20)^2} = 98.0 \,m. \end{align*} \nonumber \]
لاحظ أن تحويل لورنتز أعطى معادلة انكماش الطول للشارع.
يرى الراصد الموضح في الشكل وهو\(\PageIndex{2}\) يقف بجانب خطوط السكك الحديدية أن المصباحين يومضان في آن واحد عند طرفي سيارة الركاب التي يبلغ طولها 26 مترًا عندما يمر منتصف السيارة به بسرعة c /2. أوجد الفاصل الزمني بين وقت وميض المصابيح كما يراها راكب القطار الجالس في منتصف السيارة.
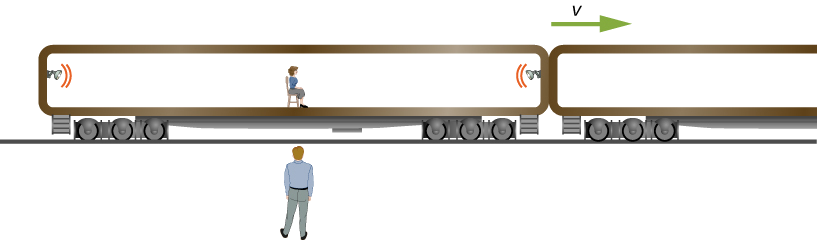
الحل
- حدد المعروف:\(\Delta t = 0\).
لاحظ أن الفصل المكاني للحدثين يقع بين المصباحين، وليس مسافة المصباح إلى الراكب.
- حدد المجهول:\(\Delta t' = t'_2 - t'_1.\).
مرة أخرى، لاحظ أن الفاصل الزمني هو بين ومضات المصابيح، وليس بين أوقات الوصول للوصول إلى الراكب.
- عبِّر عن الإجابة في صورة معادلة:
\[\Delta t = \dfrac{\Delta t' + v\Delta x'/c^2}{\sqrt{1 - v^2/c^2}}. \nonumber \]
- قم بالحساب:
\[\begin{align*} 0 &= \dfrac{\Delta t' + \dfrac{c}{2} (26 \,m)/c^2}{\sqrt{1 - v^2/c^2}} \\[4pt] \Delta t' &= - \dfrac{26 \,m/s}{2c} = - \dfrac{26 \,m/s}{2(3.00 \times 10^8 \,m/s)} \\[4pt] &= -4.33 \times 10^{-8}\,s. \end{align*} \nonumber \]
الدلالة
تشير العلامة إلى أن الحدث الأكبر،\(x'_2\) أي الفلاش من اليمين، يُنظر إليه على أنه يحدث أولاً في إطار S، كما هو موضح سابقًا في هذا المثال، لذلك\(t_2 < t_1\).
الزمكان
يمكن تحليل الظواهر النسبية من حيث الأحداث في الزمكان رباعي الأبعاد. عندما يُنظر إلى ظواهر مثل المفارقة المزدوجة، والتمدد الزمني، وانكماش الطول، واعتماد التزامن على الحركة النسبية بهذه الطريقة، يُنظر إليها على أنها مميزة لطبيعة المكان والزمان، وليس جوانب محددة من الكهرومغناطيسية.
في الفضاء ثلاثي الأبعاد، يتم تحديد المواضع بثلاثة إحداثيات على مجموعة من المحاور الديكارتية، ويتم إزاحة نقطة واحدة من أخرى من خلال:
\[(\Delta x, \,\Delta y, \,\Delta z) = (x_2 - x_1, \,y_2 - y-1, \,z_2 - z_1). \nonumber \]
المسافة\(\Delta r\) بين النقاط هي
\[\Delta r^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2. \nonumber \]
المسافة\(\Delta r\) ثابتة تحت دوران المحاور. في حالة استخدام مجموعة جديدة من المحاور الديكارتية التي تدور حول الأصل بالنسبة للمحاور الأصلية، ستحتوي كل نقطة في الفضاء على إحداثيات جديدة من حيث المحاور الجديدة، ولكن المسافة\(\Delta r'\) المعطاة بواسطة
\[\Delta r'^2 = (\Delta x')^2 + (\Delta y')^2 + (\Delta z')^2. \nonumber \]
هذا له نفس القيمة التي\(\Delta r^2\) كانت لها. يحدث شيء مماثل مع تحول لورنتز في الزمكان.
حدِّد المسافة بين حدثين، يُعطى كلٌ منهما بواسطة مجموعة من x وy وzوct على طول نظام المحاور الديكارتية رباعي الأبعاد في الزمكان، على النحو التالي:
\[(\Delta x, \,\Delta y, \,\Delta z, \,c\Delta t) = (x_2 - x_1, \,y_2 - y_1, \,z_2 - z_1, \,c(t_2 - t_1)). \nonumber \]
حدد أيضًا الفاصل الزمني بين الزمكان\(Δs\) بين الحدثين على النحو
\[\Delta s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \nonumber \]
إذا كان للحدثين نفس قيمة ct في الإطار المرجعي الذي تم النظر فيه،\(\Delta s\) فسوف يتوافق ذلك مع المسافة\(\Delta r\) بين النقاط في الفضاء.
يتكون مسار الجسيم عبر الزمكان من الأحداث (x، y، zct) التي تحدد موقعًا في كل مرة من حركته. يُطلق على المسار عبر الزمكان الخط العالمي للجسيم. الخط العالمي للجسيم الذي يظل ثابتًا في نفس الموقع هو خط مستقيم موازٍ لمحور الوقت. إذا تحرك الجسيم بسرعة ثابتة موازية لمحور x، فسيكون خطه العالمي خطًا منحدرًا\(x = vt\)، يتوافق مع رسم بياني بسيط للإزاحة مقابل الرسم البياني الزمني. إذا تسارع الجسيم، يكون خطه العالمي منحنيًا. تُعطى الزيادة في s على طول الخط العالمي للجسيم في شكل تفاضلي كـ
\[ds^2 = (dx)^2 + (dy)^2 + (dz)^2 - c^2(dt)^2. \nonumber \]
مثلما\(\Delta r\) تكون المسافة ثابتة تحت دوران محاور الفضاء، فإن فترة الزمكان:
\[\Delta s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \nonumber \]
غير متغير في ظل تحول لورنتز. يأتي هذا من افتراضات النسبية، ويمكن رؤيته أيضًا عن طريق استبدال معادلات تحويل لورنتز السابقة في التعبير عن فترة الزمكان:
\[\begin{align*} \Delta s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \\[4pt] &=\left(\dfrac{\Delta x' + v\Delta t'}{\sqrt{1 - v^2/c^2}}\right)^2 + (\Delta y')^2 + (\Delta z')^2 - \left(c\dfrac{\Delta t' + \dfrac{v\Delta x'}{c^2}}{\sqrt{1 - v^2/c^2}}\right)^2 \nonumber \]\[= (\Delta x')^2 + (\Delta y')^2 + (\Delta z')^2 - (c\Delta t')^2 \\[4pt] &= \Delta s'^2. \end{align*} \nonumber \]
بالإضافة إلى ذلك، يغير تحويل لورنتز إحداثيات الحدث في الزمان والمكان بشكل مشابه لكيفية تغيير الدوران ثلاثي الأبعاد للإحداثيات القديمة إلى إحداثيات جديدة:
|
تحويل لورنتز (إحداثيات x، t): |
المحور - الدوران حول z - المحور (إحداثيات x، t): |
|---|---|
|
\(x' = (γ)x + (−βγ)ct\) |
\(x' = (\cos θ)x + (\sin θ)y\) |
| \(ct' = (−βγ)x + (γ)ct\) | \(y' = (−\sin θ)x + (\cos θ)y\) |
أين\(\gamma = \dfrac{1}{\sqrt{1 - \beta^2}}\)؛\(\beta = v/c\).
يمكن اعتبار تحويلات لورنتز بمثابة تعميمات للتدوير المكاني إلى الزمكان. ومع ذلك، هناك بعض الاختلافات بين دوران المحور ثلاثي الأبعاد وتحويل لورنتز الذي يتضمن محور الوقت، بسبب الاختلافات في كيفية اختلاف المقياس أو القاعدة لقياس\(\Delta s\) الإزاحة\(\Delta r\) و. على الرغم من\(\Delta r\) كونه ثابتًا في ظل الدوران المكاني وغير ثابت أيضًا في إطار تحويل لورنتز، فإن تحويل لورنتز الذي يتضمن المحور الزمني لا يحافظ على بعض الميزات، مثل المحاور المتبقية عموديًا أو مقياس الطول على طول كل محور الذي يظل كما هو.\(\Delta s\)
لاحظ أن الكمية\(\Delta s^2\) يمكن أن تحتوي على أي علامة، اعتمادًا على إحداثيات أحداث الزمكان المعنية. بالنسبة لأزواج الأحداث التي تعطيها علامة سلبية، من المفيد تحديد\(c^2 \Delta \tau^2\) كـ\(-\Delta s^2\). تأتي أهمية\(c^2 \Delta \tau\) ما تم تعريفه للتو من خلال ملاحظة أنه في إطار مرجعي حيث يقع الحدثان في نفس الموقع، لدينا\(\Delta x = \Delta y = \Delta z = 0\) وبالتالي (من المعادلة لـ\(\Delta s^2 = - c^2 \Delta \tau^2\)):
\[c^2 \Delta \tau^2 = - \Delta s^2 = (c^2 \Delta t)^2. \nonumber \]
لذلك\(c^2 \Delta \tau\) هو الفاصل الزمني\(c^2 \Delta t\) في الإطار المرجعي حيث يحدث كلا الحدثين في نفس الموقع. إنها نفس الفترة الزمنية المناسبة التي تمت مناقشتها سابقًا. ويترتب أيضًا على العلاقة بين ذلك\(\Delta s\)\(c^2 \Delta \tau\) وذاك أنه نظرًا\(\Delta s\) لعدم ثبات لورنتز، فإن الوقت المناسب هو أيضًا ثابت في لورنتز. يتفق جميع المراقبين في جميع الأطر بالقصور الذاتي على الفواصل الزمنية المناسبة بين نفس الحدثين.
أظهر أنه إذا\(dt\) انقضت زيادة زمنية لراصد يرى الجسيم يتحرك بسرعة\(v\)، فإن ذلك يتوافق مع زيادة الجسيمات الزمنية المناسبة للجسيم\(d\tau = \gamma dt\).
- إجابة
-
ابدأ بتعريف الزيادة الزمنية المناسبة:
\[d\tau = \sqrt{-(ds)^2 /c^2} = \sqrt{dt^2 - (dx^2 + dx^2 + dx^2)/c^2}. \nonumber \]
حيث\((dx, dy, dx, cdt)\) يتم قياسها في إطار القصور الذاتي لمراقب لا يرى بالضرورة هذا الجسيم في حالة سكون. لذلك يصبح هذا
\[d\tau = \sqrt{-(ds)^2/c^2} = \sqrt{dt^2 - [(dx)^2 + (dy)^2 + (dz)^2]/c^2} \nonumber \]
\[dt\sqrt{1 - \left[ \left(\dfrac{dx}{dt}\right)^2 + \left(\dfrac{dy}{dt}\right)^2 + \left(\dfrac{dz}{dt}\right)^2\right] /c^2} \nonumber \]\[dt\sqrt{1 - v^2/c^2} \nonumber \]\[dt = \gamma d\tau. \nonumber \]
ذا لايت كون
يمكننا التعامل مع صعوبة تصور ورسم الرسوم البيانية في أربعة أبعاد من خلال تخيل الإحداثيات المكانية الثلاثة ليتم تمثيلها بشكل جماعي بمحور أفقي، والمحور الرأسي ليكون المحور CT. بدءًا من حدث معين في الزمكان كما هو موضح في أصل الرسم البياني للزمكان، فإن الخط العالمي للجسيم الذي يظل في حالة سكون في الموقع الأولي للحدث عند نقطة الأصل هو محور الوقت. يحتوي أي مستوى يمر عبر المحور الزمني الموازي للمحاور المكانية على جميع الأحداث المتزامنة مع بعضها البعض ومع تقاطع المستوى والمحور الزمني، كما هو موضح في الإطار المتبقي للحدث عند نقطة الأصل.
من المفيد تصوير مخروط ضوئي على الرسم البياني، يتكون من الخطوط العالمية لجميع أشعة الضوء التي تمر عبر حدث الأصل A، كما هو موضح في الشكل\(\PageIndex{3}\). يحتوي المخروط الضوئي، وفقًا لفرضيات النسبية، على جوانب بزاوية 45 درجة إذا تم قياس المحور الزمني بوحدات ct، ووفقًا لفرضيات النسبية، يظل مخروط الضوء كما هو في جميع الإطارات بالقصور الذاتي. نظرًا لأن الحدث A تعسفي، فإن كل نقطة في مخطط الزمكان لها مخروط ضوئي مرتبط بها.
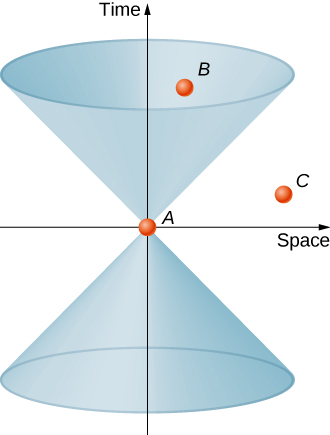
فكر الآن في الخط العالمي للجسيم عبر الزمكان. أي خط عالمي خارج المخروط، مثل الخط الذي يمر من A إلى C، سيتضمن سرعات أكبر من c، وبالتالي لن يكون ممكنًا. يقال إن الأحداث مثل C التي تقع خارج مخروط الضوء لها فصل يشبه الفضاء عن الحدث A. وهي تتميز بما يلي:
\[\Delta s_{AC}^2 = (x_A - x_C)^2 + (y_A - y_C)^2 + (z_A - z_C)^2 - (c\Delta t)^2 > 0. \nonumber \]
يمكن الوصول إلى حدث مثل B يقع في المخروط العلوي دون تجاوز سرعة الضوء في الفراغ، ويتميز بـ
\[\Delta s_{AB}^2 = (x_A - x_B)^2 + (y_A - y_B)^2 + (z_A - z_B)^2 - (c\Delta t)^2 <0. \nonumber \]
يقال إن الحدث يتميز بفصل يشبه الوقت عن A. تحدث الأحداث الشبيهة بالوقت التي تقع في النصف العلوي من مخروط الضوء بقيم t أكبر من وقت الحدث A عند قمة الرأس وتكون في المستقبل بالنسبة إلى A. الأحداث التي لها فصل يشبه الوقت عن A وتقع في النصف السفلي من مخروط الضوء كانت في الماضي، ويمكن أن تؤثر على الحدث عند الأصل. لا توصف المنطقة الواقعة خارج المخروط الخفيف بأنها ليست ماضية ولا مستقبلية، بل على أنها «في مكان آخر».
بالنسبة لأي حدث له فصل يشبه الفضاء عن الحدث في الأصل، من الممكن اختيار محور زمني يجعل الحدثين يحدثان في نفس الوقت، بحيث يكون الحدثان متزامنين في إطار مرجعي ما. لذلك، فإن أي من الأحداث ذات الفصل الشبيه بالفضاء تأتي قبل الأخرى في الوقت المناسب يعتمد أيضًا على الإطار المرجعي للمراقب. نظرًا لأن الفواصل الشبيهة بالفضاء لا يمكن اجتيازها إلا من خلال تجاوز سرعة الضوء؛ يوفر هذا الانتهاك للحدث الآخر حجة أخرى لسبب عدم قدرة الجسيمات على السفر بشكل أسرع من سرعة الضوء، بالإضافة إلى مادة محتملة للخيال العلمي حول السفر عبر الزمن. وبالمثل بالنسبة لأي حدث ذي فصل زمني يشبه الحدث في الأصل، يمكن العثور على إطار مرجعي يجعل الأحداث تحدث في نفس الموقع. لأن العلاقات
\[\Delta s_{AC}^2 = (x_A - x_C)^2 + (y_A - x_C)^2 + (z_A - z_C)^2 - (c\Delta t)^2 > 0. \nonumber \]
و
\[\Delta s_{AB}^2 = (x_A - x_B)^2 + (y_A - y_B)^2 + (z_A - z_B)^2 - (c\Delta t)^2 <0. \nonumber \]
لا تتغير حالة لورنتز، سواء أكان حدثان شبيهين بالوقت ويمكن إجراؤهما في نفس المكان أو في نفس المكان أو الفضاء ويمكن إجراؤهما في نفس الوقت أم لا بالنسبة لجميع المراقبين. يتفق جميع المراقبين في الأطر المرجعية المختلفة بالقصور الذاتي على ما إذا كان هناك حدثان لهما فصل يشبه الوقت أو الفضاء.
المفارقة المزدوجة التي نراها في الزمكان
تتضمن المفارقة المزدوجة التي تمت مناقشتها سابقًا سفر توأم رائد فضاء بسرعة قريبة من الضوء إلى نظام نجمي بعيد والعودة إلى الأرض. بسبب تمدد الوقت، من المتوقع أن يبلغ عمر التوأم الفضائي أقل بكثير من عمر التوأم المحيط بالأرض. يبدو هذا متناقضًا لأننا ربما توقعنا للوهلة الأولى أن تكون الحركة النسبية متماثلة واعتقدنا بسذاجة أنه من الممكن أيضًا القول بأن التوأم المرتبط بالأرض يجب أن يقل عمره.
لتحليل هذا من منظور مخطط الزمكان، افترض أن أصل المحاور المستخدمة ثابت في الأرض. ثم يكون الخط العالمي للتوأم المتجه إلى الأرض على طول محور الوقت.
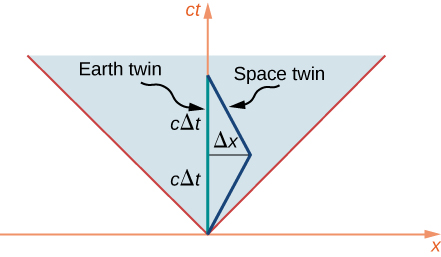
يجب أن ينحرف الخط العالمي لتوأم رائد الفضاء، الذي يسافر إلى النجم البعيد ثم يعود، عن مسار الخط المستقيم للسماح برحلة العودة. كما هو موضح في الشكل\(\PageIndex{4}\)، فإن ظروف التوأمين ليست متماثلة على الإطلاق. مساراتهم في الزمكان ذات أطوال مختلفة بشكل واضح. على وجه التحديد، يبلغ طول الخط العالمي للتوأم المتجه إلى الأرض\(2c\Delta t\)، مما يعطي الوقت المناسب الذي ينقضي بالنسبة للتوأم المحيط بالأرض\(2\Delta t\). المسافة إلى نظام النجوم البعيدة هي\(\Delta x = v\Delta t\). الوقت المناسب الذي ينقضي لتوأم الفضاء هو\(2\Delta \tau\) المكان
\[c^2\Delta \tau^2 = - \Delta s^2 = (c\Delta t)^2 - (\Delta x)^2. \nonumber \]
هذا أقصر بكثير من الوقت المناسب للتوأم القريب من الأرض حسب النسبة
\[\dfrac{c\Delta \tau}{c\Delta t} = \sqrt{\dfrac{(c\Delta t)^2 - (\Delta x)^2}{(c\Delta t)^2}} = \sqrt{\dfrac{(c\Delta t)^2 - (v\Delta t)^2}{(c\Delta t)^2}} = \sqrt{1 - \dfrac{v^2}{c^2}} = \dfrac{1}{\gamma}. \nonumber \]
بما يتفق مع صيغة تمدد الوقت. لذلك لا يُنظر إلى المفارقة المزدوجة على أنها مفارقة على الإطلاق. وضع التوأمين غير متماثل في مخطط الزمكان. ربما تكون المفاجأة الوحيدة هي أن المسار الأطول على ما يبدو في مخطط الزمكان يتوافق مع الفاصل الزمني المناسب الأصغر، بسبب كيفية\(\Delta \tau\)\(\Delta s\) الاعتماد على\(\Delta x\) و\(\Delta t\).
تحولات لورنتز في الزمكان
لقد لاحظنا بالفعل كيف يغادر تحول لورنتز
\[\Delta s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \nonumber \]
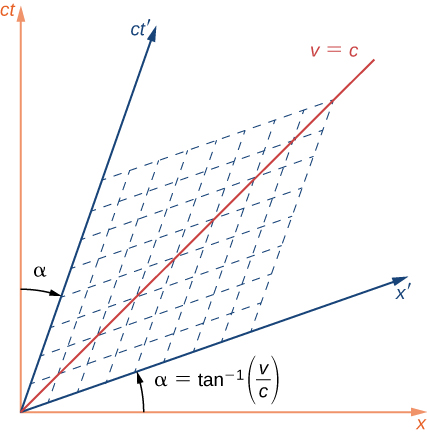
دون تغيير ويتوافق مع دوران المحاور في الزمكان رباعي الأبعاد. إذا كانت إطارات S و S في حركة نسبية على طول اتجاه x المشترك الخاص بها، يتم تدوير محاور المسافة والوقت لـ S بزاوية α كما هو موضح من S، بالطريقة الموضحة في الشكل\(\PageIndex{5}\)، حيث:
\[tan \,\alpha = \dfrac{v}{c} = \beta. \nonumber \]
يختلف هذا عن الدوران بالمعنى المعتاد ثلاثي الأبعاد، حيث يدور محورا الزمكان تجاه بعضهما البعض بشكل متماثل بطريقة تشبه المقص، كما هو موضح. يتم دوران محوري الزمان والمكان من خلال نفس الزاوية. تُظهر شبكة الخطوط المتقطعة الموازية للمحورين كيفية قراءة إحداثيات الحدث على طول المحاور الأولية. يمكن القيام بذلك عن طريق اتباع خط موازي لـ x وآخر موازي للمحور t، كما هو موضح في الخطوط المتقطعة. يتم تغيير مقياس طول كلا المحورين من خلال:
\[ct' = ct\sqrt{\dfrac{1 + \beta^2}{1 - \beta^2}}; \,x' = x\sqrt{\dfrac{1 + \beta^2}{1 - \beta^2}}. \nonumber \]
الخط المسمى «v = c» عند 45 درجة إلى المحور x يتوافق مع حافة مخروط الضوء، ولا يتأثر بتحول لورنتز، وفقًا للافتراض النسبي الثاني. الخط «v = c»، والمخروط الضوئي الذي يمثله، هما نفس الشيء لكل من الإطار المرجعي S و S.
التزامن
يعتمد تزامن الأحداث في المواقع المنفصلة على الإطار المرجعي المستخدم لوصفها، كما هو موضح في «الدوران» الشبيه بالمقص لإحداثيات الزمان والمكان الجديدة كما هو موضح. إذا كان هناك حدثان لهما نفس\(t\) القيم في الإطار المرجعي غير المُجهز، فلا يلزم أن يكون لهما نفس القيم المقاسة على طول\(ct'\) المحور -، ومن ثم لن يكونا متزامنين في الإطار الأولي.
كمثال محدد، ضع في اعتبارك القطار ذو السرعة القريبة من الضوء الذي تومض فيه مصابيح الفلاش على طرفي السيارة في وقت واحد في الإطار المرجعي لمراقب على الأرض. يظهر الرسم البياني للزمكان في الشكل\(\PageIndex{6}\). يتم تمثيل ومضات المصباحين بالنقاط المسماة «مصباح الفلاش الأيسر» و «مصباح الفلاش الأيمن» التي تقع على مخروط الضوء في الماضي. ينتقل الخط العالمي لكلتا النبضات على طول حافة مخروط الضوء للوصول إلى الراصد على الأرض في وقت واحد. وصولهم هو الحدث في الأصل. لذلك كان لا بد من انبعاثها في وقت واحد في الإطار غير المطلي، كما هو موضح بالنقطة المسماة\(t\) (كلاهما). ولكن يتم قياس الوقت على طول محور ct's في الإطار المرجعي للمراقب الجالس في منتصف سيارة القطار. لذلك في إطارها المرجعي، لم يكن حدث انبعاث المصابيح المسمى\(t'\) (يسار) و\(t'\) (يمين) متزامنًا.
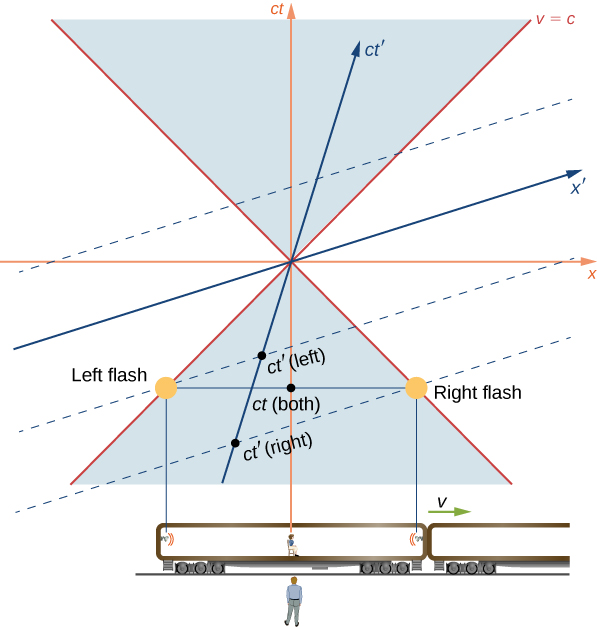
فيما يتعلق بالمخطط الزمكان، يستخدم المراقبان فقط محاور زمنية مختلفة لنفس الأحداث لأنها في إطارات مختلفة بالقصور الذاتي، واستنتاجات كلا المراقبين صحيحة بنفس القدر. كما يشير التحليل من حيث مخططات الزمكان إلى ذلك، فإن خاصية كيفية تزامن الأحداث تعتمد على الإطار المرجعي للنتائج من خصائص المكان والزمان نفسه، وليس من أي شيء يتعلق بالتحديد بالكهرومغناطيسية.


