5.5: تقلص الطول
- Page ID
- 196664
في نهاية هذا القسم، ستكون قادرًا على:
- اشرح كيف يرتبط التزامن وتقلص الطول.
- وصف العلاقة بين تقلص الطول والتمدد الزمني واستخدمها لاشتقاق معادلة الطول والانكماش.
طول عربة القطار في الشكل\(\PageIndex{1}\) هو نفسه لجميع الركاب. سيوافق كل منهم على الموقع المتزامن لطرفي السيارة والحصول على نفس النتيجة للمسافة بينهما. لكن الأحداث المتزامنة في إطار واحد بالقصور الذاتي لا يجب أن تكون متزامنة في إطار آخر. إذا كان القطار قادرًا على السفر بسرعات نسبية، فسيشاهد مراقب على الأرض المواقع المتزامنة لنقطتي نهاية السيارة على مسافة مختلفة عن المراقبين داخل السيارة. لا يجب أن تكون المسافات المقاسة هي نفسها بالنسبة للمراقبين المختلفين عندما يتعلق الأمر بسرعات نسبية.

الطول المناسب
دائمًا ما يرى مراقبان يجتازان بعضهما البعض نفس قيمة سرعتهما النسبية. على الرغم من أن تمدد الوقت يعني أن راكب القطار والمراقب الواقفين على طول المسارات يقيسان أوقاتًا مختلفة لتمرير القطار، إلا أنهم لا يزالون متفقين على أن السرعة النسبية، وهي المسافة مقسومة على الوقت المنقضي، هي نفسها. إذا قام مراقب على الأرض وآخر في القطار بقياس وقت مختلف لطول القطار لاجتياز الراصد الأرضي، فإن الاتفاق على سرعتهما النسبية يعني أنه يجب عليهما أيضًا رؤية المسافات المختلفة المقطوعة.
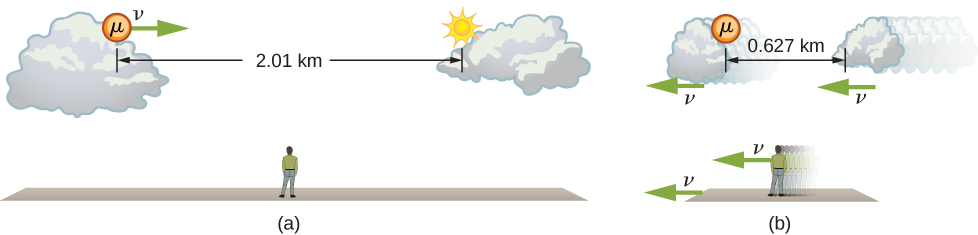
يوضح القمر الذي تمت مناقشته سابقًا هذا المفهوم (الشكل\(\PageIndex{2}\)). بالنسبة للراصد الموجود على الأرض، ينتقل الميون بسرعة 0.950 درجة مئوية لمدة 7.05 ميكروثانية من وقت إنتاجه حتى يتحلل. لذلك، فإنها تقطع مسافة بالنسبة إلى الأرض تبلغ:
\[ \begin{align*} L_0 &= v\Delta t \\[4pt] &= (0.950)(3.00 \times 10^8 \, m/s)(7.05 \times 10^{-6}s) \\[4pt] &= 2.01 \, km. \end{align*} \nonumber \]
في إطار الميون، يبلغ عمر الميون 2.20 ميكرو ثانية. في هذا الإطار المرجعي، لا يتوفر للأرض والجو والأرض سوى الوقت الكافي للسفر:
\[ \begin{align*} L &= v\Delta r \\[4pt] &= (0.950)(3.00 \times 10^8 \, m/s)(2.20 \times 10^{-6}s) \\[4pt] &= 0.627 \, km. \end{align*} \nonumber \]
تعتمد المسافة بين نفس الحدثين (إنتاج وتحلل الميون) على من يقيسه وكيف يتحرك بالنسبة إليه.
الطول المناسب\(L_0\) هو المسافة بين نقطتين يقيسها مراقب في حالة راحة بالنسبة لكلتا النقطتين.
يقيس الراصد المرتبط بالأرض الطول المناسب\(L_0\) لأن النقاط التي يتم فيها إنتاج الميون وتحللها تكون ثابتة بالنسبة للأرض. بالنسبة إلى الميون، تتحرك الأرض والهواء والغيوم، وبالتالي فإن المسافة L التي تراها ليست الطول المناسب.
تقلص الطول
لربط المسافات التي تم قياسها بواسطة مراقبين مختلفين، لاحظ أن السرعة المتعلقة بالراصد الأرضي في مثال الميون الخاص بنا تُعطى بواسطة
\[v = \dfrac{L_0}{\Delta t}. \nonumber \]
الوقت بالنسبة إلى الراصد الأرضي هو\(Δt\)، لأن الكائن الذي يتم توقيته يتحرك بالنسبة لهذا الراصد. يتم إعطاء السرعة بالنسبة للمراقب المتحرك بواسطة
\[v = \dfrac{L}{\Delta \tau}. \nonumber \]
يسافر الراصد المتحرك مع الميون وبالتالي يراقب الوقت المناسب\(\Delta \tau\). السرعتان متطابقتان؛ وبالتالي،
\[\dfrac{L_0}{\Delta t} = \dfrac{L}{\Delta \tau}. \label{eq10} \]
نحن نعلم ذلك\(\Delta t = \gamma \Delta \tau\) واستبدال هذا في المعادلة\ ref {eq10} يعطي
\[L = \dfrac{L_0}{\gamma}. \nonumber \]
يُعطي التعويض عن\(γ\) معادلة تتعلق بالمسافات التي يقيسها مراقبون مختلفون.
تقلص الطول هو الانخفاض في الطول المقاس لجسم من طوله المناسب عند قياسه في إطار مرجعي يتحرك فيما يتعلق بالكائن:
\[L = L_0\sqrt{1 - \dfrac{v^2}{c^2}} \label{contraction} \]
\(L_0\)أين طول الكائن في إطار الراحة الخاص به،\(L\) وهو الطول في الإطار الذي يتحرك بسرعة\(v\).
إذا قمنا بقياس طول أي شيء يتحرك بالنسبة لإطارنا، نجد أن طوله L أصغر من الطول المناسب\(L_0\) الذي سيتم قياسه إذا كان الكائن ثابتًا. على سبيل المثال، في إطار استراحة الميون، تكون المسافة التي تقطعها الأرض بين مكان إنتاج الميون ومكان تحللها أقصر من المسافة المقطوعة كما تُرى من إطار الأرض. هذه النقاط ثابتة بالنسبة للأرض ولكنها تتحرك بالنسبة إلى الميون. تنقبض السحب والأشياء الأخرى أيضًا على طول اتجاه الحركة كما يظهر من إطار راحة الميون.
وبالتالي، يقوم مراقبان بقياس مسافات مختلفة على طول اتجاه الحركة النسبية، اعتمادًا على الشخص الذي يقيس المسافات بين الأشياء قيد الراحة.
ولكن ماذا عن المسافات المقاسة في اتجاه عمودي على الحركة النسبية؟ تخيل مراقبين يتحركان على طول محاور x ويمرران ببعضهما البعض أثناء الإمساك بعصي العداد عموديًا في اتجاه y. \(\PageIndex{3}\)يوضِّح الشكل عصي M وM التي يبلغ طولها مترين في حالة سكون في الإطارات المرجعية لطفلين S وS'، على التوالي. يتم تثبيت فرشاة رسم صغيرة على الجزء العلوي (علامة 100 سم) من العصا M '. لنفترض أن S تتحرك إلى اليمين بسرعة v عالية جدًا بالنسبة إلى S، وأن العصي موجهة بحيث تكون متعامدة أو عرضية مع متجه السرعة النسبي. يتم تثبيت العصي بحيث تتزامن أطرافها السفلية (علامات 0 سم) عند مرورها ببعضها البعض. افترض أنه عندما ينظر S إلى عصاه M بعد ذلك، يجد خطًا مرسومًا عليها، أسفل الجزء العلوي من العصا مباشرةً. نظرًا لأن الفرشاة متصلة بالجزء العلوي من عصا الصبي الآخر M '، يمكن لـ S فقط أن تستنتج أن العصا M' يبلغ طولها أقل من 1.0 متر.
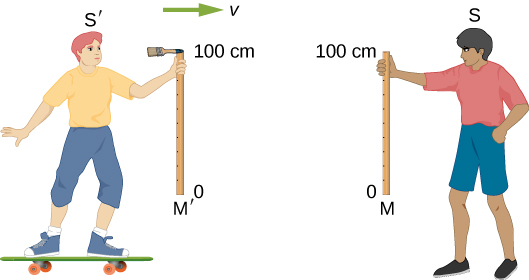
الآن عندما يقترب الأولاد من بعضهم البعض، يرى S، مثل S، عصا متر تتحرك نحوه بسرعة v. نظرًا لأن أوضاعهم متماثلة، يجب على كل صبي إجراء نفس قياس العصا في الإطار الآخر. لذلك، إذا كان طول العصا S 'M' أقل من 1.0 متر، فيجب على S' قياس العصا M ليكون طولها أقل من 1.0 متر أيضًا، ويجب أن يرى S' فرشاة الطلاء الخاصة به تمر فوق الجزء العلوي من العصا M ولا ترسم خطًا عليها. بعبارة أخرى، بعد نفس الحدث، يرى أحد الصبيين خطًا مطليًا على عصا، بينما لا يرى الآخر مثل هذا الخط على نفس العصا!
تتطلب فرضية أينشتاين الأولى أن تتنبأ قوانين الفيزياء (كما هو الحال، على سبيل المثال، المطبقة على الرسم) بأن S و S، وكلاهما في إطارات بالقصور الذاتي، يدليان بنفس الملاحظات؛ أي أن S و S يجب أن يرى كلاهما خطًا مرسومًا على العصا M، أو كلاهما لا يرى هذا الخط. لذلك نحن مضطرون إلى استنتاج أن افتراضنا الأصلي بأن S رأى خطًا مرسومًا أسفل الجزء العلوي من عصاه كان خاطئًا! بدلاً من ذلك، يجد S الخط المرسوم مباشرة عند علامة 100 سم على M. ثم يوافق كلا الصبيان على رسم الخط على M، وسيتفقان أيضًا على أن طول العصيتين 1 متر بالضبط. نستنتج بعد ذلك أن القياسات ذات الطول العرضي يجب أن تكون هي نفسها في إطارات القصور الذاتي المختلفة.
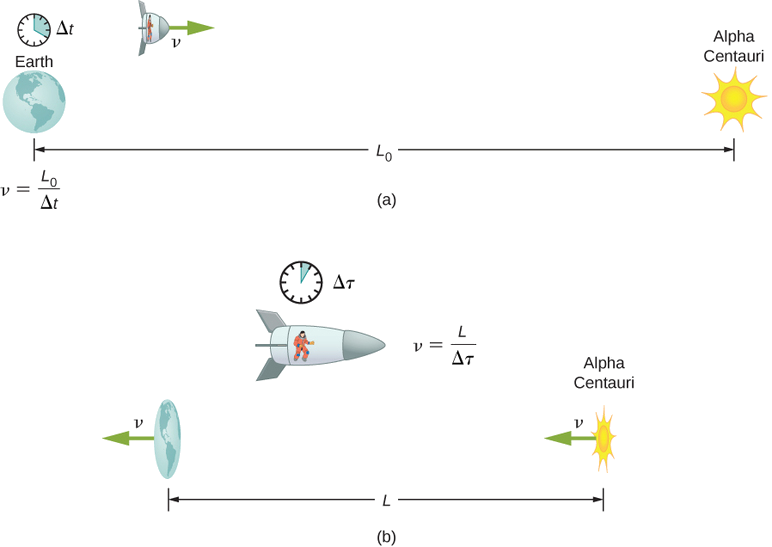
لنفترض أن رائد الفضاء، مثل التوأم في مناقشة المفارقة المزدوجة، يسافر بسرعة كبيرة\(\gamma = 30.00\). (أ) ينتقل رائد الفضاء من الأرض إلى أقرب نظام نجمي، وهو Alpha Centauri، على بعد 4.300 سنة ضوئية (ly) حسب قياسه بواسطة راصد محدق بالأرض. ما مدى المسافة بين الأرض وألفا سنتوري كما قاسها رائد الفضاء؟ (ب) من حيث c، ما هي سرعة رائد الفضاء بالنسبة للأرض؟ قد تهمل حركة الأرض بالنسبة للشمس (الشكل\(\PageIndex{4}\)).
إستراتيجية
أولاً، لاحظ أن السنة الضوئية (ly) هي وحدة ملائمة للمسافة على مقياس فلكي - إنها المسافة التي يقطعها الضوء في السنة. بالنسبة للجزء (أ)، فإن المسافة التي تبلغ 4.300 متر بين ألفا سنتوري والأرض هي المسافة المناسبة\(L_0\)، لأنها تقاس بواسطة مراقب أرضي يكون كلا النجمين ثابتين له (تقريبًا). بالنسبة لرائد الفضاء، تتحرك الأرض وألفا سنتوري في الماضي بنفس السرعة، وبالتالي فإن المسافة بينهما هي الطول المتعاقد L. في الجزء (ب)، تم إعطاؤنا\(\gamma\)، حتى نتمكن\(v\) من العثور عليه من\(\gamma\) خلال إعادة ترتيب تعريف التعبير من\(v\) حيث\(c\).
حل لـ (أ)
بالنسبة للجزء (أ):
- التعرف على الأشياء المعروفة:\(L_0 = 4.300 \, ly\)؛\(\gamma = 30.00.\)
- حدد المجهول: L.
- عبّر عن الإجابة كمعادلة:\(L = \dfrac{L_0}{\gamma}\).
- قم بالحساب:
\[\begin{align*} L &= \dfrac{L_0}{\gamma} \\[4pt] &= \dfrac{4.300 \, ly}{30.00} \\[4pt] &= 0.1433 \, ly. \end{align*} \nonumber \]
حل لـ (ب)
بالنسبة للجزء (ب):
- حدد المعروف:\(\gamma = 30.00\).
- حدد المجهول: v من حيث c.
- عبِّر عن الإجابة في صورة معادلة. ابدأ بـ:
\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]
ثم قم بحل الخطأ المجهول v/c عن طريق تربيع كلا الجانبين أولاً ثم إعادة الترتيب:\[\begin{align*} \gamma^2 &= \dfrac{1}{1 - \dfrac{v^2}{c^2}} \\[4pt] \dfrac{v^2}{c^2} &= 1 - \dfrac{1}{\gamma^2} \\[4pt] \dfrac{v}{c} &= \sqrt{1 - \dfrac{1}{\gamma^2}}. \end{align*} \nonumber \]
- قم بالحساب:
\[\begin{align*} \dfrac{v}{c} &= \sqrt{1 - \dfrac{1}{\gamma^2}} \\[4pt] &= \sqrt{1 - \dfrac{1}{(30.00)^2}} \\[4pt] &= 0.99944\end{align*} \nonumber \]
أو\[v = 0.9994 \, c. \nonumber \]
الأهمية: تذكر عدم إنهاء العمليات الحسابية حتى الإجابة النهائية، أو قد تحصل على نتائج خاطئة. وينطبق هذا بشكل خاص على حسابات النسبية الخاصة، حيث لا يمكن الكشف عن الاختلافات إلا بعد عدة أرقام عشرية. التأثير النسبي كبير هنا (\(\gamma = 30.00\))، ونرى أن v تقترب (لا تساوي) سرعة الضوء. نظرًا لأن المسافة التي قاسها رائد الفضاء أصغر بكثير، يمكن لرائد الفضاء أن يقطعها في وقت أقل بكثير في إطارها.
يمكن للأشخاص الذين يسافرون بسرعات عالية للغاية أن يقطعوا مسافات كبيرة جدًا (آلاف أو حتى ملايين السنين الضوئية) وأن يكبروا بضع سنوات فقط في الطريق. ومع ذلك، مثل المهاجرين في القرون الماضية الذين تركوا وطنهم، فإن هؤلاء الناس سيغادرون الأرض التي يعرفونها إلى الأبد. حتى لو عادوا، لمرت آلاف وملايين السنين على الأرض، مما أدى إلى القضاء على معظم ما هو موجود الآن. هناك أيضًا عقبة عملية أكثر خطورة للسفر بهذه السرعات؛ ستكون هناك حاجة إلى طاقات أكبر بكثير لتحقيق مثل هذه السرعات العالية مما تتوقعه الفيزياء الكلاسيكية. سيتم مناقشة هذا لاحقًا في الفصل.
لماذا لا نلاحظ تقلص الطول في الحياة اليومية؟ لا يبدو أن المسافة إلى متجر البقالة تعتمد على ما إذا كنا نتحرك أم لا. عند فحص المعادلة\ ref {contraction}، نرى أنه عند السرعات المنخفضة (\(v \ll c\))، تكون الأطوال متساوية تقريبًا، وهو التوقع الكلاسيكي. ومع ذلك، فإن تقلص الطول حقيقي، إن لم يكن شائعًا. على سبيل المثال، يحتوي الجسيم المشحون مثل الإلكترون الذي يتحرك بسرعة نسبية على خطوط مجال كهربائي يتم ضغطها على طول اتجاه الحركة كما يراها مراقب ثابت (الشكل\(\PageIndex{5}\)). عندما يمر الإلكترون بكاشف، مثل ملف من الأسلاك، يتفاعل مجاله بشكل أقصر بكثير، وهو تأثير لوحظ في مسرعات الجسيمات مثل معجل ستانفورد الخطي (SLAC) الذي يبلغ طوله 3 كيلومترات. في الواقع، بالنسبة للإلكترون الذي ينتقل عبر أنبوب الشعاع في SLAC، يتحرك المسرع والأرض جميعًا ويتم تقلصهما. التأثير النسبي كبير جدًا لدرجة أن المسرع يبلغ طول الإلكترون 0.5 متر فقط. في الواقع، من الأسهل إخراج شعاع الإلكترون من الأنبوب، لأن الشعاع لا يجب أن يكون موجهًا بدقة للوصول إلى أنبوب قصير كما هو الحال عند النزول إلى أنبوب بطول 3 كم. هذا، مرة أخرى، هو التحقق التجريبي من نظرية النسبية الخاصة.
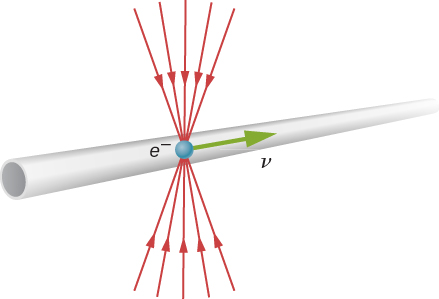
ينتقل جسيم عبر الغلاف الجوي للأرض بسرعة تبلغ\(0.750c\). بالنسبة للراصد الموجود على الأرض، فإن المسافة التي يقطعها هي 2.50 كم. ما المسافة التي يقطعها الجسيم كما يُرى من الإطار المرجعي للجسيم؟
- إجابة
-
\[L = L_0\sqrt{1 - \dfrac{v^2}{c^2}} = (2.50 \, km)\sqrt{1 - \dfrac{(0.750c)^2}{c^2}} = 1.65 \, km \nonumber \]


