5.4: تمدد الوقت

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

• اشرح كيف يمكن قياس الفواصل الزمنية بشكل مختلف في إطارات مرجعية مختلفة.
• وصف كيفية التمييز بين الفاصل الزمني المناسب والفاصل الزمني الموسع.
• وصف أهمية تجربة الميونات.
• اشرح لماذا لا تعتبر المفارقة المزدوجة تناقضًا.
• احسب الامتداد الزمني بمعلومية سرعة جسم في إطار معين.

يُظهر تحليل التزامن أن افتراضات أينشتاين تنطوي على تأثير مهم: الفواصل الزمنية لها قيم مختلفة عند قياسها في إطارات مختلفة بالقصور الذاتي. لنفترض، على سبيل المثال، أن رائد الفضاء يقيس الوقت الذي تستغرقه نبضة الضوء لقطع مسافة عمودية على اتجاه حركة سفينته (بالنسبة إلى مراقب أرضي)، والارتداد عن المرآة، والعودة (الشكل\(\PageIndex{1a}\)). كيف يُقارن الوقت المنقضي الذي يقيسه رائد الفضاء في المركبة الفضائية بالوقت المنقضي الذي يقيسه المراقب الأرضي من خلال مراقبة ما يحدث في المركبة الفضائية؟

دراسة هذا السؤال تؤدي إلى نتيجة عميقة. يعتمد الوقت المنقضي للعملية على المراقب الذي يقيسها. في هذه الحالة، يكون الوقت الذي يقيسه رائد الفضاء (داخل سفينة الفضاء حيث يكون رائد الفضاء في حالة راحة) أصغر من الوقت الذي يقيسه الراصد الأرضي (الذي ينتقل إليه رائد الفضاء). ويختلف الوقت المنقضي لنفس العملية بالنسبة للمراقبين، لأن المسافة التي تقطعها نبضة الضوء في إطار رائد الفضاء أصغر منها في الإطار الأرضي، كما هو موضح في الشكل\(\PageIndex{1b}\). ينتقل الضوء بنفس السرعة في كل إطار، لذلك يستغرق الأمر وقتًا أطول لقطع المسافة الأكبر في الإطار الأرضي.

الشكل\(\PageIndex{1}\): (أ) يقيس رائد الفضاء الوقت الذي\(\Delta \tau\) يستغرقه الضوء في قطع مسافة 2D في إطار رائد الفضاء. (ب) يرى أحد علماء ناسا على الأرض أن الضوء يتبع المسار الأطول 2 ثانية ويستغرق وقتًا أطول\(\Delta t\). (ج) تستخدم هذه المثلثات لإيجاد العلاقة بين المسافتين D و s.

تعريف: تمدد الوقت

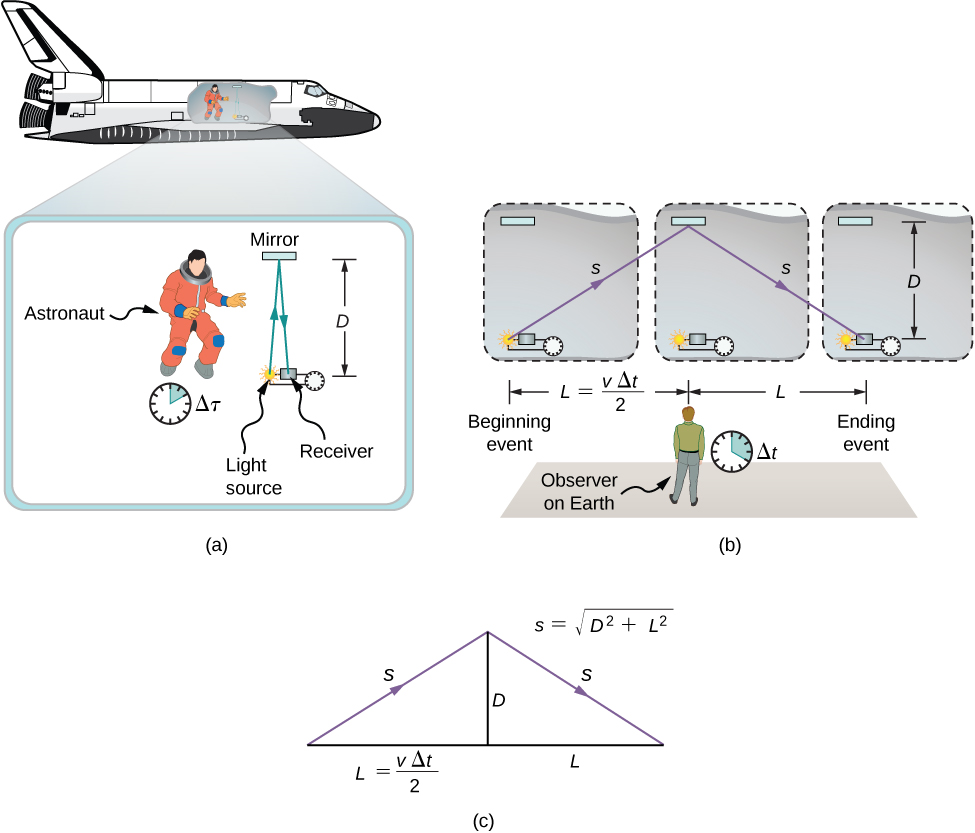
التمدد الزمني هو إطالة الفاصل الزمني بين حدثين للمراقب في إطار القصور الذاتي الذي يتحرك فيما يتعلق بالإطار المتبقي للأحداث (حيث تحدث الأحداث في نفس الموقع).

للمقارنة الكمية للقياسات الزمنية في الإطارين بالقصور الذاتي، يمكننا ربط المسافات في الشكل\(\PageIndex{1b}\) ببعضها البعض، ثم التعبير عن كل مسافة من حيث وقت السفر (على التوالي إما\(\Delta t\) أو\(\Delta \tau\)) للنبض في الإطار المرجعي المقابل. يمكن بعد ذلك حل المعادلة الناتجة من\(\Delta t\) حيث\(\Delta \tau\).

الأطوال\(D\) والشكل\(L\)\(\PageIndex{1c}\) هي أضلاع مثلث قائم الزاوية مع وتر\(s\). من نظرية فيثاغورس،

\[s^2 = D^2 + L^2. \nonumber \]

الأطوال\(2s\)\(2L\) وهي، على التوالي، المسافات التي تقطعها نبضة الضوء والمركبة الفضائية بمرور الوقت\(\Delta t\) في إطار الراصد الأرضي. الطول\(D\) هو المسافة التي تقطعها نبضة الضوء بمرور الوقت\(\Delta \tau\) في إطار رائد الفضاء. هذا يعطينا ثلاث معادلات:

\[\begin{align*} 2s &= c\Delta t \\[4pt] 2L &= v\Delta t; \\[4pt] 2D &= c\Delta \tau. \end{align*} \nonumber \]

لاحظ أننا استخدمنا الافتراض الثاني لأينشتاين من خلال جعل سرعة الضوء c في كلا الإطارين بالقصور الذاتي. نستبدل هذه النتائج بالتعبير السابق من نظرية فيثاغورس:

\[ \begin{align*} s^2 &= D^2 + L^2 \\[4pt] \left(c\dfrac{\Delta t}{2}\right)^2 &= \left(c\dfrac{\Delta \tau}{2}\right)^2 + \left(v\dfrac{\Delta t}{2}\right)^2 \end{align*} \nonumber \]

ثم نعيد الترتيب للحصول على

\[(c\Delta t)^2 - (v\Delta t)^2 = (c\Delta \tau)^2. \nonumber \]

أخيرًا،\(\Delta \tau\) يمنحنا الحل من منظور\(\Delta t\)

\[\Delta t = \dfrac{\Delta \tau}{\sqrt{1 - (v/c)^2}}. \nonumber \]

هذا يعادل

\[\Delta t = \gamma \Delta \tau, \label{timedilation} \]

أين\(\gamma\) هو العامل النسبي (الذي يُطلق عليه غالبًا عامل لورنتز) الذي قدمه

\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}} \nonumber \]

\(v\)\(c\)وهي سرعات الراصد المتحرك والضوء على التوالي.

لاحظ عدم التماثل بين القياسين. واحد منهم فقط هو قياس الفاصل الزمني بين حدثين - انبعاث ووصول نبضة الضوء - في نفس الموضع. إنه قياس للفاصل الزمني في الإطار المتبقي لساعة واحدة. يتضمن القياس في الإطار الأرضي مقارنة الفاصل الزمني بين حدثين يحدثان في مواقع مختلفة. الفاصل الزمني بين الأحداث التي تحدث في موقع واحد له اسم منفصل لتمييزه عن الوقت الذي يقيسه الراصد الأرضي، ونستخدم الرمز المنفصل للإشارة\(\Delta \tau\) إليه طوال هذا الفصل.

تعريف: الوقت المناسب

الفاصل الزمني المناسب\(\Delta \tau\) بين حدثين هو الفاصل الزمني الذي يقيسه مراقب يقع كلا الحدثين له في نفس الموقع.

المعادلة المتعلقة\(\delta t\)\(\Delta \tau\) وهي رائعة حقًا. أولاً، كما ذكرنا سابقًا، الوقت المنقضي ليس هو نفسه بالنسبة للمراقبين المختلفين الذين يتحركون بالنسبة لبعضهم البعض، على الرغم من أن كلاهما في إطارات بالقصور الذاتي. الفاصل الزمني المناسب\(\Delta \tau\) للمراقب الذي يتحرك مع الجهاز، مثل رائد الفضاء، أصغر من الفاصل الزمني للمراقبين الآخرين. إنه أصغر وقت مُقاس ممكن بين حدثين. يرى الراصد المرتبط بالأرض الفواصل الزمنية داخل النظام المتحرك على أنها ممتدة (أي مطولة) بالنسبة لكيفية رؤية الراصد المتحرك بالنسبة للأرض داخل النظام المتحرك. بدلاً من ذلك، وفقًا للمراقب الأرضي، يمر وقت أقل بين الأحداث داخل الإطار المتحرك. لاحظ أن أقصر فترة زمنية بين الأحداث هي في إطار القصور الذاتي الذي يرى فيه الراصد الأحداث (على سبيل المثال، انبعاث ووصول إشارة الضوء) تحدث في نفس النقطة.

هذا التأثير الزمني حقيقي ولا ينتج عن ساعات غير دقيقة أو قياسات غير صحيحة. تختلف قياسات الفاصل الزمني لنفس الحدث بالنسبة للمراقبين في الحركة النسبية. تمدد الوقت هو خاصية جوهرية للوقت نفسه. يُلاحظ أن جميع الساعات التي تتحرك بالنسبة إلى الراصد، بما في ذلك الساعات البيولوجية، مثل نبضات قلب الشخص، أو الشيخوخة، تعمل ببطء أكثر مقارنة بالساعة الثابتة بالنسبة للمراقب.

لاحظ أنه إذا كانت السرعة النسبية أقل بكثير من سرعة الضوء (v << c)، فستكون صغيرة\(v^2/c^2\) جدًا، والأوقات\(\Delta t\) المنقضية ومتساوية تقريبًا.\(\Delta \tau\) في السرعات المنخفضة، تقترب الفيزياء القائمة على النسبية الحديثة من الفيزياء الكلاسيكية - تتضمن التجارب اليومية تأثيرات نسبية صغيرة جدًا. ومع ذلك، بالنسبة للسرعات القريبة من سرعة الضوء،\(v^2/c^2\) تكون قريبة من واحدة، لذا\(\sqrt{1 - v^2/c^2}\) فهي صغيرة جدًا\(\Delta t\) وتصبح أكبر بكثير من\(\Delta \tau\).

هاف-لايف أوف مون

هناك أدلة تجريبية كبيرة على أن المعادلة\(\Delta t = \gamma \Delta \tau\) صحيحة. يوجد أحد الأمثلة في جزيئات الأشعة الكونية التي تمطر باستمرار على الأرض من الفضاء السحيق. تؤدي بعض اصطدامات هذه الجسيمات بالنواة في الغلاف الجوي العلوي إلى جزيئات قصيرة العمر تسمى الميونات. يبلغ عمر النصف (مقدار الوقت الذي يستغرقه تحلل نصف المادة) للميون 1.52 ميكروثانية عندما يكون في حالة راحة بالنسبة للمراقب الذي يقيس نصف العمر. هذه هي الفترة الزمنية المناسبة\(\Delta \tau\). يسمح هذا الوقت القصير لعدد قليل جدًا من الميونات بالوصول إلى سطح الأرض واكتشافها إذا كانت الافتراضات النيوتونية حول الزمان والمكان صحيحة. ومع ذلك، فإن الميونات التي تنتجها جزيئات الأشعة الكونية لها مجموعة من السرعات، حيث يتحرك بعضها بالقرب من سرعة الضوء. لقد وجد أن نصف عمر الميون كما تم قياسه بواسطة مراقب مرتبط بالأرض (\(\Delta t\)) يختلف بالسرعة تمامًا كما تنبأت المعادلة\(\Delta t = \gamma \Delta \tau\). كلما تحركت الميون بشكل أسرع، كلما طالت مدة حياته. نحن على الأرض نرى الميون يدوم لفترة أطول بكثير مما يتوقعه نصف عمره ضمن إطار الراحة الخاص به. كما هو موضح من إطارنا، يتحلل الميون ببطء أكثر مما يحدث عندما يكون في حالة راحة بالنسبة لنا. ونتيجة لذلك، يصل جزء أكبر بكثير من الميونات إلى الأرض.

قبل أن نقدم المثال الأول لحل مشكلة في النسبية، نضع استراتيجية يمكنك استخدامها كمبدأ توجيهي لهذه الحسابات.

إستراتيجية حل المشكلات: النسبية

1. قم بعمل قائمة بما هو معطى أو يمكن استنتاجه من المشكلة كما هو مذكور (حدد المعروف). ابحث بشكل خاص عن معلومات حول السرعة النسبية v.
2. حدد بالضبط ما يجب تحديده في المشكلة (حدد المجهول).
3. تأكد من فهمك للجوانب المفاهيمية للمشكلة قبل إجراء أي حسابات (عبر عن الإجابة كمعادلة). حدد، على سبيل المثال، أي مراقب يرى الوقت متوسعًا أو طولًا متقلصًا قبل التعامل مع المعادلات أو استخدامها لإجراء الحساب. إذا فكرت في من يرى ماذا، ومن يتحرك مع الحدث الذي تتم ملاحظته، ومن يرى الوقت المناسب، وما إلى ذلك، ستجد أنه من الأسهل بكثير تحديد ما إذا كانت عملية الحساب الخاصة بك معقولة.
4. حدد نوع الحساب الأساسي الذي يجب القيام به للعثور على المجهول المحدد أعلاه (قم بالحساب). ستجد ملخص القسم مفيدًا في تحديد ما إذا كان هناك تقلص الطول أو الطاقة الحركية النسبية أو بعض المفاهيم الأخرى.

لاحظ أنه يجب ألا تنتهي أثناء الحساب. كما هو موضح في النص، يجب عليك غالبًا إجراء العمليات الحسابية إلى العديد من الأرقام لرؤية التأثير المطلوب. يمكنك الانتهاء في نهاية حل المشكلة، ولكن لا تستخدم رقمًا مقربًا في عملية حسابية لاحقة. تحقق أيضًا من الإجابة لمعرفة ما إذا كانت معقولة: هل لها معنى؟ قد يكون هذا أكثر صعوبة بالنسبة للنسبية، التي لديها القليل من الأمثلة اليومية لتوفير الخبرة مع ما هو معقول. ولكن يمكنك البحث عن سرعات أكبر من c أو التأثيرات النسبية التي تسير في الاتجاه الخاطئ (مثل الانكماش الزمني حيث كان من المتوقع حدوث تمدد).

مثال\(\PageIndex{1A}\): Time Dilation in a High-Speed Vehicle

مركبة التكنولوجيا الفائقة الصوت 2 (HTV-2) هي مركبة صاروخية تجريبية قادرة على السفر بسرعة 21000 كم/ساعة (5830 م/ث). إذا كانت الساعة الإلكترونية في HTV-2 تقيس فاصلًا زمنيًا مدته 1 ثانية بالضبط، فما الذي يمكن للمراقبين على الأرض قياسه؟

إستراتيجية

قم بتطبيق صيغة التمدد الزمني لربط الفاصل الزمني المناسب للإشارة في HTV-2 بالفاصل الزمني المقاس على الأرض.

الحل

1. التعرف على الأشياء المعروفة\(\Delta \tau = 1 \, s\):\(v = 5830m/s.\)
2. حدد المجهول:\(\Delta t\).
3. عبِّر عن الإجابة في صورة معادلة:

   \[\Delta t = \gamma \Delta \tau = \dfrac{\Delta \tau}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]

4. قم بالحساب. استخدم التعبير\(\gamma\) للتحديد\(\Delta t\) من\(\Delta \tau\):

   \[\begin{align*} \Delta t &= \dfrac{1 \, s}{\sqrt{1 - \left(\dfrac{5830 \, m/s}{3.00 \times 10^8 m/s}\right)^2}} \\[4pt] &= 1.000000000189 \, s \\[4pt] &= 1 \, s + 1.89 \times 10^{-10}s. \end{align*} \nonumber \]

الدلالة

لا تزال السرعة العالية جدًا لـ HTV-2 تبلغ 10 ^{إلى 5} أضعاف سرعة الضوء فقط. التأثيرات النسبية لـ HTV-2 ضئيلة لجميع الأغراض تقريبًا، ولكنها ليست صفرية.

ما هي السرعات النسبية؟

ما مدى السرعة التي يجب أن تسير بها السيارة لمدة ثانية واحدة من الوقت الذي تم قياسه على ساعة الراكب في السيارة ليختلف بنسبة 1٪ بالنسبة للمراقب الذي يقيسها من الأرض بالخارج؟

إستراتيجية

استخدم صيغة التمدد الزمني للعثور على v/c لنسبة المرات المعطاة.

الحل

1. حدد المعروف:

   \[\dfrac{\Delta \tau}{\Delta t} = \dfrac{1}{1.01}. \nonumber \]

2. حدد المجهول: v/c.
3. عبِّر عن الإجابة في صورة معادلة:

   \[ \begin{align*} \Delta t &= \gamma \Delta \tau \\[4pt] &= \dfrac{1}{\sqrt{1 - v^2/c^2}}\Delta \tau \\[4pt] \dfrac{\Delta \tau}{\Delta t} &= \sqrt{1 - v^2/c^2} \\[4pt] \left(\dfrac{\Delta \tau}{\Delta t}\right)^2 &= 1 - \dfrac{v^2}{c^2} \\[4pt] \dfrac{v}{c} &= \sqrt{1 - (\Delta \tau/\Delta t)^2}. \end{align*} \nonumber \]

4. قم بالحساب:

   \[\dfrac{v}{c} = \sqrt{1 - (1/1.01)^2} = 0.14. \nonumber \]

الدلالة

تظهر النتيجة أن الجسم يجب أن يتحرك بنسبة 10٪ تقريبًا من سرعة الضوء حتى تنتج حركته تأثيرات تمدد زمنية نسبية كبيرة.

\(\Delta t\)حساب حدث نسبي

لنفترض أن شعاعًا كونيًا يصطدم بنواة في الغلاف الجوي العلوي للأرض ينتج ميونًا له سرعة\(v = 0.950c\). ثم ينتقل الميون بسرعة ثابتة ويعيش 2.20 ميكروثانية كما تم قياسه في الإطار المرجعي للميون. (يمكنك تخيل هذا كساعة الميون الداخلية.) كم من الوقت يعيش الميون كما تم قياسه بواسطة مراقب مرتبط بالأرض (الشكل\(\PageIndex{2}\))؟

الشكل\(\PageIndex{2}\): يعيش الميون في الغلاف الجوي للأرض لفترة أطول عند قياسه بواسطة مراقب مرتبط بالأرض مقارنة بالساعة الداخلية للمون.

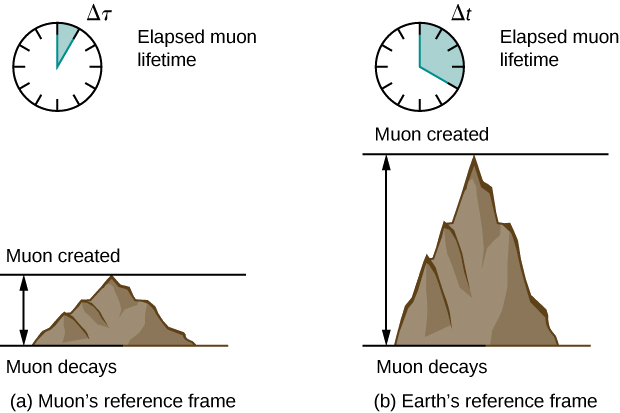
كما سنناقش لاحقًا، في الإطار المرجعي للميون، فإنه يقطع مسافة أقصر مما تم قياسه في الإطار المرجعي للأرض.

إستراتيجية

تقيس الساعة التي تتحرك مع الميون الوقت المناسب لعملية الاضمحلال، وبالتالي فإن الوقت الممنوح لنا هو\(\Delta \tau = 2.20 \mu s\). يقيس الراصد الأرضي\(\Delta t\) كما هو موضح في المعادلة\(\Delta t = \gamma \Delta \tau\). نظرًا لأن السرعة مُعطاة، يمكننا حساب الوقت في الإطار المرجعي للأرض.

الحل

1. التعرف على الأشياء المعروفة:\(v = 0.950c\)؛\(\delta \tau = 2.20 \mu s\).
2. حدد المجهول:\(\Delta t\).
3. عبِّر عن الإجابة في صورة معادلة. استخدم:

   \[\Delta t = \gamma \Delta \tau. \nonumber \]

   مع

   \[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]

4. قم بالحساب. استخدم التعبير\(\gamma\) للتحديد\(\Delta t\) من\(\Delta \tau\):

   \[\begin{align*} \Delta t &= \gamma \Delta \tau. \\[4pt] &=\dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}\delta \tau \\[4pt] &=\dfrac{2.20 \mu s}{\sqrt{1 - (0.950)^2}} \\[4pt] &= 7.05 \, \mu s.\end{align*} \nonumber \]

   تذكر الاحتفاظ بأرقام مهمة إضافية حتى الإجابة النهائية.

الدلالة

أحد الآثار المترتبة على هذا المثال هو أنه نظرًا لأن التأثيرات النسبية مهمة\(\gamma = 3.20\) عند 95.0٪ من سرعة الضوء (\(v = 0.950c\)). تختلف الفواصل الزمنية بعامل 3.20، عندما تكون هي نفسها من الناحية الكلاسيكية. يُقال إن شيئًا يتحرك عند 0.950 درجة مئوية يعتبر نسبيًا للغاية.

مثال\(\PageIndex{1B}\): Relativistic Television

تعمل شاشة التلفزيون ذات الطراز القديم غير المسطحة (الشكل\(\PageIndex{3}\)) عن طريق تسريع الإلكترونات عبر مسافة قصيرة إلى السرعة النسبية، ثم استخدام المجالات الكهرومغناطيسية للتحكم في مكان اصطدام شعاع الإلكترون بطبقة فلورية في مقدمة الأنبوب. لنفترض أن الإلكترونات تنتقل\(6.00 \times 10^7 m/s\) عبر مسافة 0.200m0.200m من بداية الشعاع إلى الشاشة.

1. ما وقت سفر الإلكترون في إطار الراحة بجهاز التلفزيون؟
2. ما وقت انتقال الإلكترون في إطار الراحة الخاص به؟

الشكل\(\PageIndex{3}\): شعاع الإلكترون في شاشة تلفزيون أنبوب أشعة الكاثود.

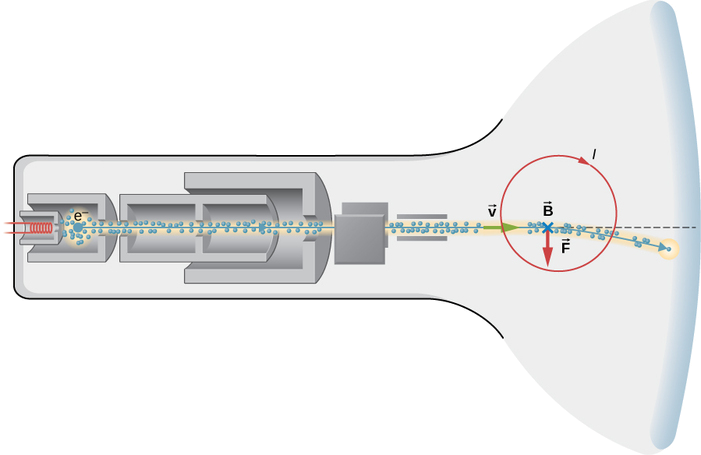
استراتيجية لـ (أ)

(أ) احسب الوقت من\(vt = d\). على الرغم من أن السرعة نسبية، إلا أن الحساب يتم بالكامل في إطار مرجعي واحد، وبالتالي لا يتم تضمين النسبية.

الحل

1. التعرف على الأشياء المعروفة:

   \[v = 6.00 \times 10^7 m/s \, d = 0.200 \, m. \nonumber \]

2. حدد المجهول: وقت السفر\(\Delta t\).
3. عبِّر عن الإجابة في صورة معادلة:

   \[\Delta t = \dfrac{d}{v}. \nonumber \]

4. قم بالحساب:

   \[ \begin{align*} t &= \dfrac{0.200 \, m}{6.00 \times 10^7 \, m/s} \\[4pt] &= 3.33 \times 10^{-9} \, s. \end{align*} \nonumber \]

الدلالة

وقت السفر قصير للغاية، كما هو متوقع. نظرًا لأن الحساب يتم بالكامل ضمن إطار مرجعي واحد، لا يتم تضمين النسبية، على الرغم من أن سرعة الإلكترون قريبة من c.

استراتيجية لـ (ب)

(ب) في الإطار المرجعي للإلكترون، يتحرك الأنبوب الفراغي ويكون الإلكترون ثابتًا. يترك الكاثود الباعث للإلكترون الإلكترون ويضرب الجزء الأمامي من الأنبوب الفراغي الإلكترون بالإلكترون في نفس الموقع. لذلك نستخدم صيغة التمدد الزمني لربط الوقت المناسب في إطار استراحة الإلكترون بالوقت في إطار التلفزيون.

الحل

1. حدد المعروف (من الجزء أ):

   \[\Delta t = 3.33 \times 10^{-9} \, s; \, v = 6.00 \times 10^7 \, m/s; \, d = 0.200 \, m. \nonumber \]

2. حدد المجهول:\(\tau\).
3. عبِّر عن الإجابة في صورة معادلة:

   \[\Delta t = \gamma \Delta \tau = \dfrac{\Delta \tau}{\sqrt{1 - v^2/c^2}}. \nonumber \]

4. قم بالحساب:

   \[\begin{align*} \Delta \tau &= (3.33 \times 10^{-9}s)\sqrt{1 - \left(\dfrac{6.00 \times 10^7 m/s}{3.00 \times 10^8 m/s}\right)^2} \\[4pt] &= 3.26 \times 10^{-9}s. \end{align*} \nonumber \]

الدلالة

يكون وقت السفر أقصر في الإطار المرجعي للإلكترون. ونظرًا لأن المشكلة تتطلب العثور على الفاصل الزمني المقاس في إطارات مرجعية مختلفة لنفس العملية، فإن الأمر يتعلق بالنسبية. إذا حاولنا حساب الوقت في إطار راحة الإلكترون بمجرد قسمة 0.200 m على السرعة، فستكون النتيجة غير صحيحة بعض الشيء بسبب السرعة النسبية للإلكترون.

التمارين\(\PageIndex{1}\)

ماذا\(\gamma\) لو\(v = 0.650c\)؟

إجابة

\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}} = \dfrac{1}{\sqrt{1 - \dfrac{(0.650c)}{c^2}}} = 1.32 \nonumber \]

مفارقة التوأم

النتيجة المثيرة للاهتمام لتمديد الوقت هي أن مسافر الفضاء الذي يتحرك بسرعة عالية بالنسبة للأرض سيكون عمره أقل من عمر توأم رائد الفضاء القريب من الأرض. يُعرف هذا غالبًا باسم المفارقة المزدوجة. تخيل رائد الفضاء يتحرك بهذه السرعة\(\gamma = 30.0\)، كما في الشكل\(\PageIndex{4}\). تستغرق الرحلة التي تستغرق 2.00 عامًا في إطارها 60.0 عامًا في إطار التوأم الأرضي. لنفترض أن رائد الفضاء سافر في عام واحد إلى نظام نجمي آخر، واستكشف المنطقة لفترة وجيزة، ثم سافر عائدًا إلى عام واحد. سيكون رائد الفضاء الذي كان يبلغ من العمر 40 عامًا في بداية الرحلة 42 عامًا عندما تعود سفينة الفضاء. ومع ذلك، سيكون عمر كل شيء على وجه الأرض 60.0 عامًا. سيكون التوأم المتجه إلى الأرض، إذا كان لا يزال على قيد الحياة، يبلغ من العمر 100 عام.

قد يبدو الوضع مختلفًا لرائد الفضاء في الشكل\(\PageIndex{4}\). نظرًا لأن الحركة نسبية، ستبدو سفينة الفضاء ثابتة ويبدو أن الأرض تتحرك. (هذا هو الإحساس الذي تشعر به عند الطيران في طائرة.) عند النظر من نافذة سفينة الفضاء، سيرى رائد الفضاء تباطؤ الوقت على الأرض بعامل\(\gamma = 30.0\). وعند رؤيته من سفينة الفضاء، سيكون عمر الأخ القريب من الأرض 2/30 أو 0.07 عامًا فقط، في حين أن رائد الفضاء سيكون قد بلغ من العمر 2.00 عامًا.

الشكل\(\PageIndex{4}\): تتكون المفارقة المزدوجة من الاستنتاجات المتضاربة حول أي توأم يتقدم في العمر نتيجة رحلة فضائية طويلة بسرعة نسبية.

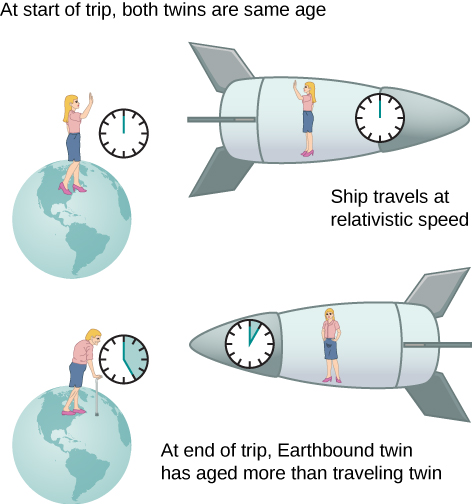
المفارقة هنا هي أن التوأم لا يمكن أن يكونا صحيحين. كما هو الحال مع جميع المفارقات، تأتي الاستنتاجات المتضاربة من فرضية خاطئة. في الواقع، تختلف حركة رائد الفضاء اختلافًا كبيرًا عن حركة التوأم المتجه إلى الأرض. يتسارع رائد الفضاء إلى سرعة عالية ثم يتباطأ لمشاهدة النظام النجمي. للعودة إلى الأرض، تتسارع وتتباطأ مرة أخرى. المركبة الفضائية ليست في إطار واحد بالقصور الذاتي يمكن تطبيق صيغة التمدد الزمني عليه مباشرة. أي أن توأم رائد الفضاء يغير المراجع بالقصور الذاتي. لا يواجه التوأم المتجه إلى الأرض هذه التسارعات ويبقى في نفس الإطار بالقصور الذاتي. وبالتالي، فإن الوضع ليس متماثلًا، ومن غير الصحيح الادعاء بأن رائدة الفضاء تلاحظ نفس تأثيرات توأمها. سيظل عدم التماثل بين التوائم أكثر وضوحًا عندما نحلل الرحلة لاحقًا في هذا الفصل من حيث المسار الذي يتبعه رائد الفضاء خلال الزمكان رباعي الأبعاد.

في عام 1971، تحقق الفيزيائيان الأمريكيان جوزيف هافيل وريتشارد كيتنغ من التمدد الزمني بسرعات نسبية منخفضة من خلال الطيران بساعات ذرية دقيقة للغاية حول العالم على متن طائرات تجارية. قاموا بقياس الوقت المنقضي بدقة تبلغ بضع نانوثانية ومقارنته بالوقت الذي تم قياسه بالساعات المتبقية. كانت نتائج Hafele و Keating ضمن حالات عدم اليقين التجريبية لتوقعات النسبية. يجب أخذ كل من النسبية الخاصة والعامة في الاعتبار، لأن الجاذبية والتسارع كانت متورطة وكذلك الحركة النسبية.

التمارين\(\PageIndex{2A}\)

أ- ينتقل الجسيم\(1.90 \times 10^8 \, m/s\) ويعيش\(2.1 \times 10^8 \, s\) عندما يكون في حالة راحة بالنسبة للراصد. ما المدة التي يعيش فيها الجسيم كما يُرى في المختبر؟

إجابة

\[\Delta t = \dfrac{\Delta \tau}{\sqrt{1 - \dfrac{v^2}{c^2}}} = \dfrac{2.10 \times 10^{-8}s}{\sqrt{1 - \dfrac{(1.90 \times 10^8 \, m/s)^2}{(3.00 \times 10^8 \, m/s)^2}}} = 2.71 \times 10^{-8} \, s. \nonumber \]

التمارين\(\PageIndex{2B}\)

تمر المركبة الفضائية A و B في اتجاهين متعاكسين بسرعة نسبية تبلغ\(4.00 \times 10^7 \, m/s\). تتسبب الساعة الداخلية في المركبة الفضائية A في إصدار إشارة لاسلكية لمدة 1.00 ثانية. ويقوم الكمبيوتر الموجود في المركبة الفضائية B بتصحيح بداية ونهاية الإشارة التي قطعت مسافات مختلفة، لحساب الفاصل الزمني الذي كانت السفينة A ترسل خلاله الإشارة. ما الفترة الزمنية التي يحسبها الكمبيوتر في المركبة الفضائية B؟

إجابة

فقط السرعة النسبية للمركبتين الفضائيتين مهمة لأنه لا توجد حركة مطلقة عبر الفضاء. تنبعث الإشارة من موقع ثابت في الإطار المرجعي لـ A، وبالتالي فإن الفاصل الزمني المناسب لانبعاثها هو\(\tau = 1.00 \, s\). يتم بعد ذلك تحديد مدة الإشارة المقاسة من الإطار المرجعي B

\[\Delta t = \dfrac{\Delta \tau}{\sqrt{1 - \dfrac{v^2}{c^2}}} = \dfrac{1.00 \, s}{\sqrt{1 - \dfrac{(4.00 \times 10^7 \, m/s)^2}{(3.00 \times 10^8 \, m/s)^2}}} = 1.01 \, s. \nonumber \]