2.9: المجاهر والتلسكوبات
- Page ID
- 196770
في نهاية هذا القسم، ستكون قادرًا على:
- شرح الفيزياء وراء تشغيل المجاهر والتلسكوبات
- وصف الصورة التي تم إنشاؤها بواسطة هذه الأدوات وحساب تكبيرها
تعد الميكروسكوبات والتلسكوبات من الأدوات الرئيسية التي ساهمت بشكل كبير في فهمنا الحالي للعوالم الدقيقة والميكروسكوبية. أدى اختراع هذه الأجهزة إلى العديد من الاكتشافات في تخصصات مثل الفيزياء وعلم الفلك وعلم الأحياء، على سبيل المثال لا الحصر. في هذا القسم، نشرح الفيزياء الأساسية التي تجعل هذه الأدوات تعمل.
مجاهر
على الرغم من أن العين رائعة في قدرتها على رؤية الأشياء الكبيرة والصغيرة، فمن الواضح أنها محدودة في أصغر التفاصيل التي يمكنها اكتشافها. أدت الرغبة في رؤية ما وراء ما هو ممكن بالعين المجردة إلى استخدام الأدوات البصرية. لقد رأينا أن العدسة المحدبة البسيطة يمكنها إنشاء صورة مكبرة، ولكن من الصعب الحصول على تكبير كبير باستخدام هذه العدسة. من الصعب إجراء تكبير أكبر من 5 × دون تشويه الصورة. للحصول على نسبة تكبير أعلى، يمكننا دمج العدسة المكبرة البسيطة مع عدسة إضافية واحدة أو أكثر. في هذا القسم، نقوم بفحص المجاهر التي تعمل على تكبير التفاصيل التي لا يمكننا رؤيتها بالعين المجردة.
تم تطوير الميكروسكوبات لأول مرة في أوائل القرن السادس عشر من قبل صانعي النظارات في هولندا والدنمارك. يتكون أبسط مجهر مركب من عدستين محدبتين (الشكل\(\PageIndex{1}\)). العدسة الموضوعية هي عدسة محدبة ذات طول بؤري قصير (أي طاقة عالية) مع تكبير نموذجي من 5 × إلى 100 ×. العدسة، التي يشار إليها أيضًا باسم العين، هي عدسة محدبة ذات طول بؤري أطول.
الغرض من المجهر هو إنشاء صور مكبرة للأجسام الصغيرة، وتساهم كلتا العدستين في التكبير النهائي. أيضًا، يتم إنتاج الصورة المكبرة النهائية بعيدًا بما يكفي عن الراصد بحيث يمكن مشاهدتها بسهولة، حيث لا يمكن للعين التركيز على الأشياء أو الصور القريبة جدًا (أي الأقرب من النقطة القريبة للعين).
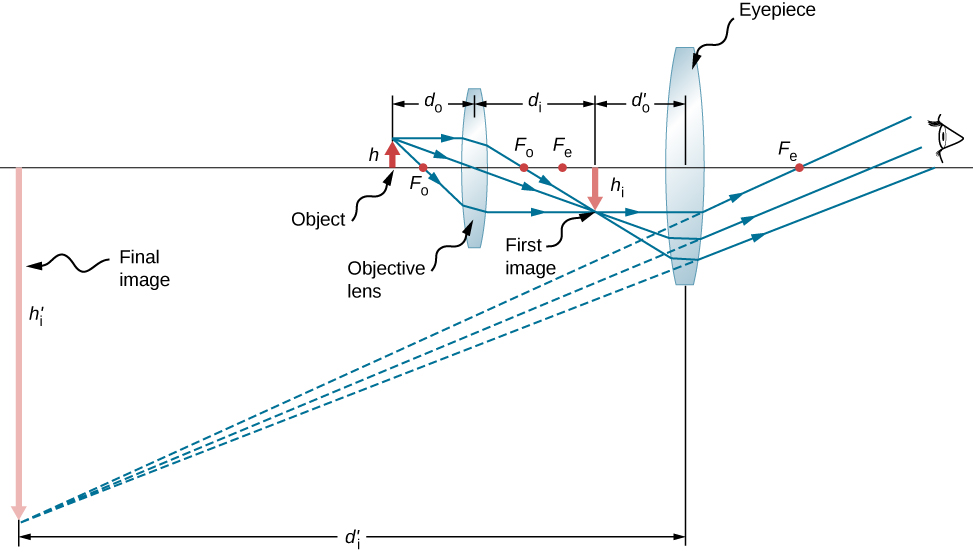
لمعرفة كيفية قيام المجهر في الشكل\(\PageIndex{1}\) بتشكيل صورة، ضع في اعتبارك العدستين المتتابعتين. يتجاوز الجسم البُعد البؤري\(f^{obj}\) للعدسة الموضوعية، مما ينتج صورة حقيقية مقلوبة أكبر من الكائن. تُستخدم هذه الصورة الأولى ككائن للعدسة الثانية أو العدسة. يتم وضع العدسة بحيث تكون الصورة الأولى ضمن البعد البؤري\(f^{eye}\)، بحيث يمكنها تكبير الصورة بشكل أكبر. بمعنى ما، تعمل كعدسة مكبرة تعمل على تكبير الصورة الوسيطة التي ينتجها الهدف. الصورة التي تنتجها العدسة هي صورة افتراضية مكبرة. تظل الصورة النهائية معكوسة ولكنها أبعد عن المراقب عن الكائن، مما يجعل من السهل عرضها.
ترى العين الصورة الافتراضية التي تم إنشاؤها بواسطة العدسة، والتي تعمل ككائن للعدسة في العين. تكون الصورة الافتراضية التي تشكلها العدسة خارج البعد البؤري للعين بشكل كبير، لذلك تشكل العين صورة حقيقية على شبكية العين.
تكبير المجهر هو نتاج التكبير\(m^{obj}\) الخطي بالهدف والتكبير الزاوي\(M^{eye}\) بواسطة العدسة. يتم تقديم هذه بواسطة
\ ابدأ {محاذاة *}
و\ الجزء السفلي {m^ {o b j} =-\ frac {d_ {i} {o b j}} {d_ {o} {d_ {o} {o b j}\ تقريبًا-\ frac {d_ {i} ^ {o b j}} {f^ {o b j}}} _ {\\\ النص {التكبير الخطي حسب الهدف}}\
\\ {M^ {e y e} =1+\ frac {25 سم} {f^ {e y e}}} _ {\ النص {التكبير الزاوي بواسطة العدسة}}
\ نهاية {محاذاة *}
هنا،\(f^{obj}\) وهذه\(f^{eye}\) هي الأطوال البؤرية للهدف والعدسة، على التوالي. نفترض أن الصورة النهائية تتشكل عند النقطة القريبة للعين، مما يوفر أكبر قدر من التكبير. لاحظ أن التكبير الزاوي للعدسة هو نفسه الذي تم الحصول عليه سابقًا للعدسة المكبرة البسيطة. لا ينبغي أن يكون هذا مفاجئًا، لأن العدسة هي في الأساس عدسة مكبرة، وتنطبق نفس الفيزياء هنا. التكبير\(M_{net}\) الصافي للمجهر المركب هو نتاج التكبير الخطي للهدف والتكبير الزاوي للعدسة:
\[ M_{\mathrm{net}}=m^{\mathrm{obj}} M^{\mathrm{eye}}=-\frac{d_{\mathrm{i}}^{\mathrm{obj}}\left(f^{\mathrm{eye}}+25 \mathrm{cm}\right)}{f^{\mathrm{obj}} f^{\mathrm{eye}}} \label{2.34} . \]
احسب نسبة تكبير جسم وُضع على بُعد ٦٫٢٠ مم من مجهر مركب هدفه البُعد البؤري ٦٫٠٠ مم والعدسة ذات البُعد البؤري ٥٫٠ مم. يتم فصل الهدف والعدسة بمقدار 23.0 سم.
إستراتيجية
تتشابه هذه الحالة مع تلك الموضحة في الشكل\(\PageIndex{1}\). للعثور على التكبير الكلي، يجب أن نعرف التكبير الخطي للهدف والتكبير الزاوي للعدسة. يمكننا استخدام Equation\ ref {2.34}، لكننا نحتاج إلى استخدام معادلة العدسة الرقيقة للعثور على مسافة\(d^{obj}_i\) الصورة للهدف.
الحل
حل معادلة العدسة الرقيقة لـ\(d^{obj}_i\) Gives
\ ابدأ {محاذاة} d^ {obj} _ {i} &=\ يسار (\ dfrac {1} {f^ {obj}} −\ dfrac {1} {d^ {obj} _o}\ يمين) ^ {−1}\\ [5pt] &=\ يسار (\ dfrac {1} {1} {6.00\، مم} -\ dfrac {1} {6.20 مم}\ يمين) ^ {−1}\\ [5 بت] &=186\، مم\\ [5 بت] &= 18.6\، سم\ النهاية {محاذاة}
إدراج هذه النتيجة في المعادلة\ ref {2.34} مع القيم المعروفة
- \(f^{obj} = 6.00 \, mm = 0.600 \, cm\)
- \(f^{eye} = 50.0 mm = 5.00 cm \)
يعطي
\ ابدأ {align*} M_ {net} &=−\ dfrac {d^ {obj} _i (f^ {العين} +25\، سم)} {f^ {obj} f^ {العين}\\ [5pt] &=−\ dfrac {(18.6\، سم) (5.00\ سم) (5.00\، سم) (5.00\ سم)، سم)}\\ [5pt] &=−186\ النهاية {align*}
الأهمية
يساهم كل من الهدف والعدسة في التكبير الكلي، الذي يكون كبيرًا وسلبيًا، بما يتوافق مع الشكل\(\PageIndex{1}\)، حيث يُنظر إلى الصورة على أنها كبيرة ومقلوبة. في هذه الحالة، تكون الصورة افتراضية ومعكوسة، وهو ما لا يمكن أن يحدث لعنصر واحد.
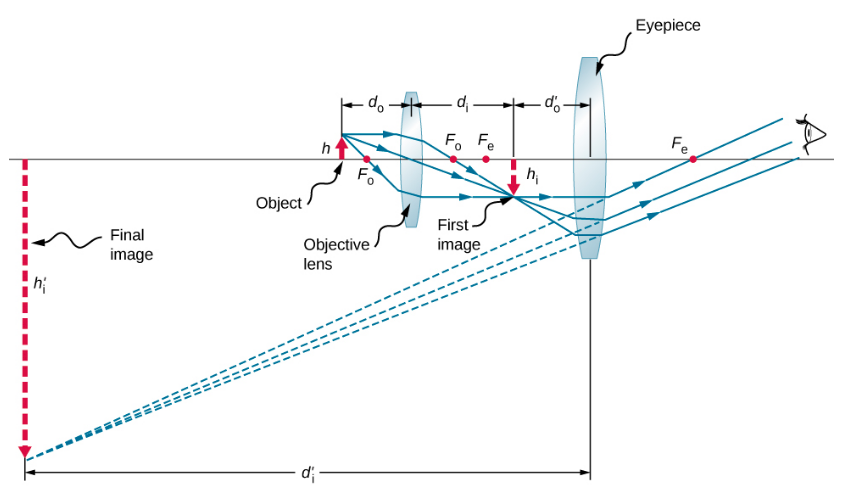
نحسب الآن القدرة المكبرة للمجهر عندما تكون الصورة عند اللانهاية، كما هو موضح في الشكل\(\PageIndex{2}\)، لأن هذا يجعل المشاهدة أكثر راحة. القوة المكبرة للمجهر هي\(m^{obj}\) نتاج التكبير الخطي للهدف والتكبير الزاوي\(M^{eye}\) للعدسة. نحن نعلم ذلك
\[ m^{obj}=−\dfrac{d^{obj}_i}{d^{obj}_o} \nonumber \]
ومن معادلة العدسة الرقيقة التي نحصل عليها
\[ m^{\mathrm{obj}}=-\frac{d_{\mathrm{i}}^{\mathrm{obj}}}{d_{\mathrm{o}}^{\mathrm{obj}}}=1-\frac{d_{\mathrm{i}}^{\mathrm{obj}}}{f^{\mathrm{obj}}}=\frac{f^{\mathrm{obj}}-d_{\mathrm{i}}^{\mathrm{obj}}}{f^{\mathrm{obj}}} \label{2.35}. \]
إذا كانت الصورة النهائية عند اللانهاية، فيجب وضع الصورة التي تم إنشاؤها بواسطة الهدف في النقطة المحورية للعدسة. يمكن ملاحظة ذلك من خلال النظر في معادلة العدسة الرقيقة مع\(d_i = \infty\) أو من خلال التذكير بأن الأشعة التي تمر عبر النقطة البؤرية تخرج من العدسة بالتوازي مع بعضها البعض، وهو ما يعادل التركيز عند اللانهاية. بالنسبة للعديد من المجاهر، يتم توحيد المسافة بين النقطة البؤرية لجانب الصورة للهدف والنقطة البؤرية لجانب الكائن للعدسة عند L = 16 سم. هذه المسافة تسمى طول أنبوب المجهر. من الشكل\(\PageIndex{2}\)، نرى ذلك
\[ L=f^{obj}−d^{obj}_i . \nonumber \]
إدراج هذا في المعادلة\ ref {2.35} يعطي
\[ m^{obj}=\dfrac{L}{f^{obj}}=\dfrac{16cm}{f^{obj}}. \label{eq2.36} \]
نحتاج الآن إلى حساب التكبير الزاوي للعدسة مع الصورة عند اللانهاية. وللقيام بذلك، نأخذ نسبة الزاوية\(\theta_{image}\) المقابلة للصورة إلى الزاوية\(\theta_{object}\) المقابلة للجسم عند النقطة القريبة من العين (وهذا هو أقرب ما يمكن للعين المجردة من رؤية الكائن فيه)، وبالتالي هذا هو الموضع الذي سيشكل فيه الكائن أكبر صورة على شبكية العين عين غير مساعدة). باستخدام الشكل\(\PageIndex{2}\) والعمل في تقريب الزوايا الصغيرة، لدينا
\[ \theta_{i m a g e} \approx \frac{h_{i}^{o b j}}{f^{e y e}} \nonumber \]
و
\[ \theta_{\text {object}} \approx \frac{h_{i}^{o b j}}{25 c m} \nonumber \]
\(h_{i}^{obj}\)أين ارتفاع الصورة التي شكلها الهدف، وهو هدف العدسة. وبالتالي، فإن التكبير الزاوي للعدسة هو
\[ M^{\text {eye }}=\frac{\theta_{\text {image }}}{\theta_{\text {object }}}=\frac{h_{i}^{\text {obj }}}{f^{\text {eye }}} \frac{25 \mathrm{cm}}{h_{i}^{\text {obj }}}=\frac{25 \mathrm{cm}}{f^{\text {eye }}} .\label{2.37} \]
وبالتالي فإن القوة المكبرة الصافية للمجهر المركب مع الصورة عند اللانهاية هي
\[ M_{net}=m^{obj}M^{eye}=−\dfrac{(16cm)(25cm)}{f^{obj}f^{eye}}. \label{2.38} \]
يجب أن تكون المسافات البؤرية بالسنتيمتر. تشير علامة الطرح إلى أن الصورة النهائية معكوسة. لاحظ أن المتغيرات الوحيدة في المعادلة هي المسافات البؤرية للعدسة والهدف، مما يجعل هذه المعادلة مفيدة بشكل خاص.
التلسكوب
تهدف التلسكوبات إلى عرض الأشياء البعيدة وإنتاج صورة أكبر من الصورة المنتجة في العين بدون مساعدة. تجمع التلسكوبات ضوءًا أكثر بكثير من العين، مما يسمح بمراقبة الأجسام المعتمة بتكبير أكبر ودقة أفضل. تم اختراع التلسكوبات حوالي عام 1600، وكان غاليليو أول من استخدمها لدراسة السماء، مع عواقب هائلة. لاحظ أقمار المشتري، والحفر والجبال على القمر، وتفاصيل البقع الشمسية، وحقيقة أن درب التبانة يتكون من عدد كبير من النجوم الفردية.
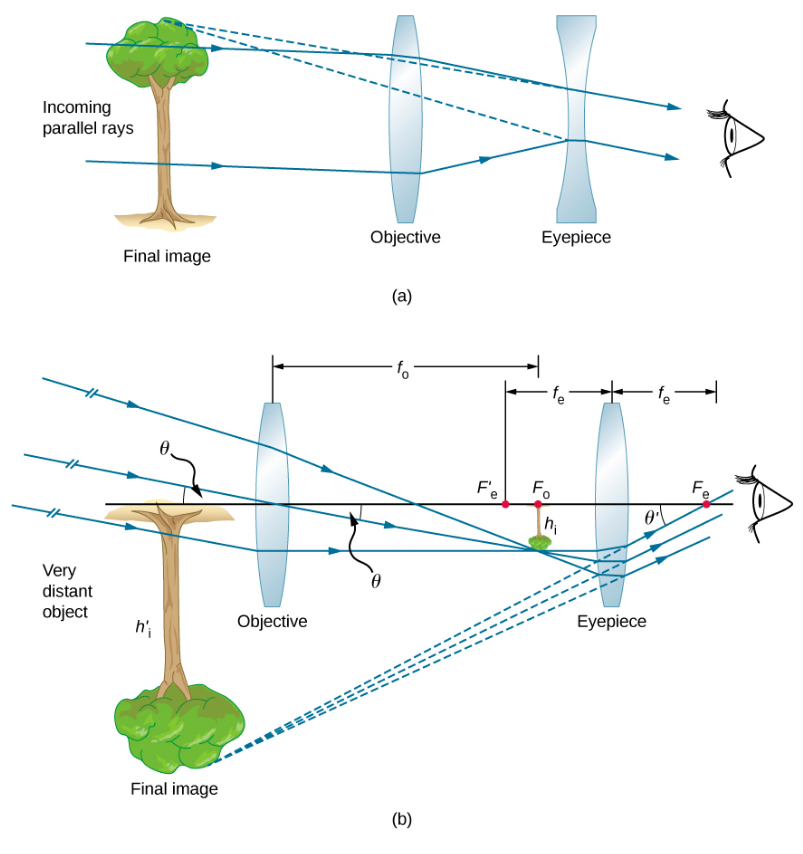
\(\PageIndex{3a}\)يوضِّح الشكل مقرابًا مكسورًا مصنوعًا من عدستين. تشكل العدسة الأولى، التي تسمى الهدف، صورة حقيقية ضمن البعد البؤري للعدسة الثانية، والتي تسمى العدسة. تعمل صورة العدسة الموضوعية كهدف للعدسة، والتي تشكل صورة افتراضية مكبرة تلاحظها العين. هذا التصميم هو ما استخدمه غاليليو لمراقبة السماء.
على الرغم من أن ترتيب العدسات في التلسكوب المنكسر يشبه ترتيب العدسات في المجهر، إلا أن هناك اختلافات مهمة. في التلسكوب، يكون الكائن الحقيقي بعيدًا والصورة المتوسطة أصغر من الكائن. في المجهر، يكون الكائن الحقيقي قريبًا جدًا والصورة المتوسطة أكبر من الكائن. في كل من التلسكوب والميكروسكوب، تقوم العدسة بتكبير الصورة المتوسطة؛ ولكن هذا هو التكبير الوحيد في التلسكوب.
يظهر التلسكوب ثنائي العدسة الأكثر شيوعًا في الشكل\(\PageIndex{3b}\). الجسم بعيد جدًا عن التلسكوب بحيث يكون أساسًا عند اللانهاية مقارنة بالأطوال البؤرية للعدسات\(d_{o}^{obj} \approx \infty \)، لذا فإن الأشعة الواردة متوازية بشكل أساسي وتركز على المستوى البؤري. وبالتالي، يتم إنتاج الصورة الأولى في
\[ d_{i}^{obj} = f^{obj} \nonumber \]
كما هو موضح في الشكل، وهي ليست كبيرة مقارنة بما قد تراه من خلال النظر مباشرة إلى الكائن. ومع ذلك، فإن عدسة عدسة التلسكوب (مثل عدسة المجهر) تسمح لك بالاقتراب من النقطة القريبة من هذه الصورة الأولى وبالتالي تكبيرها (لأنك قريب منها، فإنها تقلل من زاوية أكبر من عينك وبالتالي تشكل صورة أكبر على شبكية العين). بالنسبة للمكبر البسيط، فإن التكبير الزاوي للتلسكوب هو نسبة الزاوية المصاحبة للصورة (\(\theta_{image}\)in\(\PageIndex{3b}\)) إلى الزاوية الفرعية للكائن الحقيقي (\(\theta_{object}\)in\(\PageIndex{3b}\)):
\[ M=\dfrac{θ_{image}}{θ_{object}}. \label{2.39} \]
للحصول على تعبير للتكبير يتضمن معايير العدسة فقط، لاحظ أن المستوى البؤري للعدسة الموضوعية قريب جدًا من الخطة البؤرية للعدسة. إذا افترضنا أن هذه الطائرات متراكبة، فلدينا الموقف الموضح في الشكل\(\PageIndex{4}\).
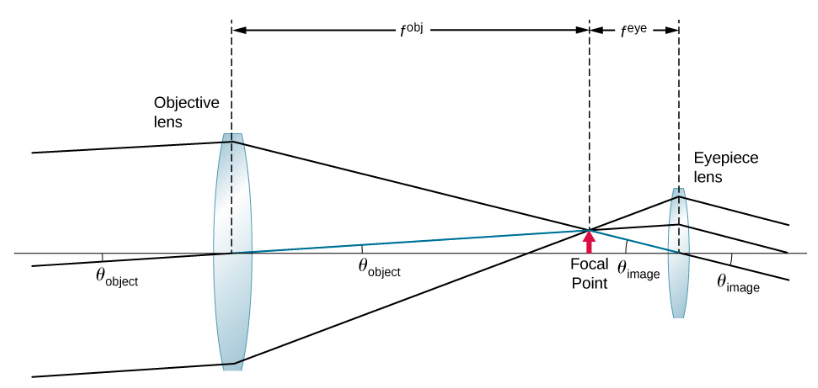
نفترض أيضًا أن الزوايا\(\theta_{object}\) والصغر\(\theta_{image}\) صغيرتان، بحيث يثبت تقريب الملاك الصغير (\(\tan \theta \approx \theta\)). إذا كانت الصورة المتكونة على المستوى البؤري لها ارتفاع،\(h\) فعندئذٍ
\ ابدأ {المصفوفة} {l}
\ theta_ {\ النص {الكائن}\ تقريبًا\ tan\ theta_ {\ text {الكائن} =\ frac {h} {f^ {\ text {obj}}
\ بدون رقم\\\\ theta_ {\ text {\ text {-h} {\ text {-h} {f^ {عين}\ بدون رقم
\ نهاية {مصفوفة}
حيث يتم إدخال علامة الطرح لأن الارتفاع يكون سالبًا إذا قمنا بقياس كلتا الزاويتين في اتجاه عكس اتجاه عقارب الساعة. إدراج هذه التعبيرات في المعادلة\ ref {2.39} يعطي
\[ M=\frac{-h_{\mathrm{i}}}{f^{\mathrm{eye}}} \frac{f^{\mathrm{obj}}}{h_{\mathrm{i}}}=-\frac{f^{\mathrm{obj}}}{f^{\mathrm{eye}}} \label{2.40}. \]
وبالتالي، للحصول على أكبر تكبير زاوي، من الأفضل أن يكون لديك هدف بطول بؤري طويل وعدسة ذات طول بؤري قصير. كلما زاد التكبير الزاوي\(M\)، زاد حجم الكائن عند مشاهدته من خلال التلسكوب، مما يجعل المزيد من التفاصيل مرئية. يتم فرض قيود على التفاصيل التي يمكن ملاحظتها من خلال العديد من العوامل، بما في ذلك جودة العدسة واضطراب الغلاف الجوي. العدسات النموذجية لها أطوال بؤرية تبلغ 2.5 سم أو 1.25 سم. إذا كان هدف التلسكوب له طول بؤري يبلغ 1 متر، فإن هذه العدسات تؤدي إلى تكبير 40× و 80×، على التوالي. وبالتالي، فإن التكبير الزاوي يجعل الصورة تظهر 40 مرة أو 80 مرة أقرب من الكائن الحقيقي.
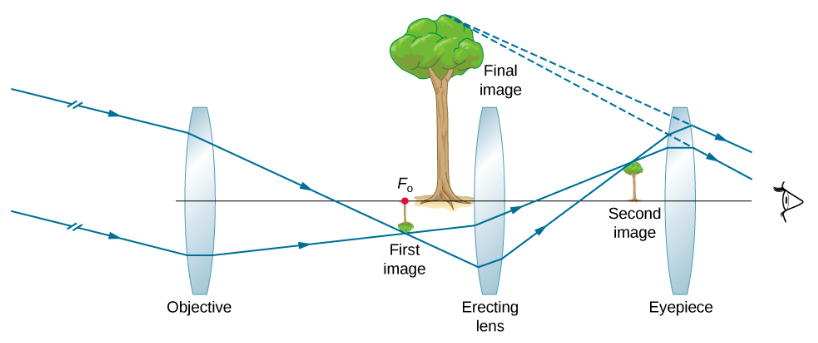
تشير علامة الطرح في التكبير إلى أن الصورة معكوسة، وهو أمر غير مهم لرصد النجوم ولكنه يمثل مشكلة حقيقية للتطبيقات الأخرى، مثل التلسكوبات على السفن أو مشاهد البندقية التلسكوبية. في حالة الحاجة إلى صورة عمودية،\(\PageIndex{3a}\) يمكن استخدام ترتيب Galileo. ولكن الترتيب الأكثر شيوعًا هو استخدام عدسة محدبة ثالثة كعدسة، وزيادة المسافة بين الأولين وعكس الصورة مرة أخرى، كما هو موضح في الشكل\(\PageIndex{5}\).
أكبر تلسكوب انكساري في العالم هو تلسكوب Yerkes بقطر 40 بوصة الموجود في بحيرة جنيف، ويسكونسن (الشكل\(\PageIndex{6}\))، وتشغله جامعة شيكاغو.
من الصعب والمكلف جدًا بناء تلسكوبات انكسارية كبيرة. تحتاج إلى عدسات كبيرة خالية من العيوب، وهي في حد ذاتها مهمة تتطلب الكثير من الناحية الفنية. يشبه التلسكوب المنكسر أساسًا أنبوبًا بهيكل داعم لتدويره في اتجاهات مختلفة. يعاني التلسكوب المنكسر من عدة مشاكل. يؤدي انحراف العدسات إلى عدم وضوح الصورة. أيضًا، عندما تصبح العدسات أكثر سمكًا للعدسات الأكبر، يتم امتصاص المزيد من الضوء، مما يجعل مراقبة النجوم الخافتة أكثر صعوبة. العدسات الكبيرة أيضًا ثقيلة جدًا وتتشوه تحت وزنها. تتم معالجة بعض هذه المشكلات المتعلقة بالتلسكوبات الانكسارية من خلال تجنب الانكسار لجمع الضوء واستخدام مرآة منحنية بدلاً من ذلك في مكانها، وفقًا لما ابتكره إسحاق نيوتن. تسمى هذه التلسكوبات العاكسة.

تلسكوبات عاكسة
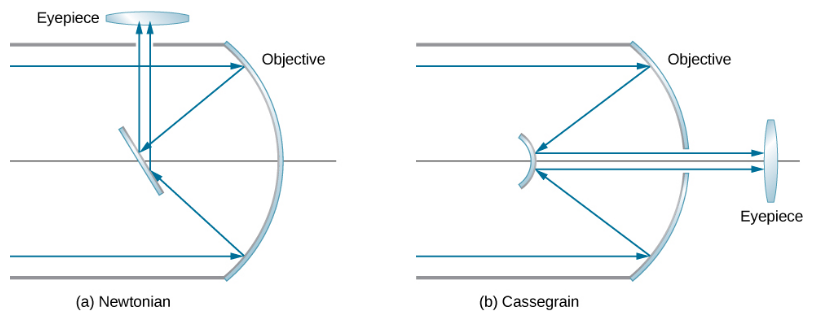
صمم إسحاق نيوتن أول تلسكوب عاكس حوالي عام 1670 لحل مشكلة الانحراف اللوني الذي يحدث في جميع التلسكوبات المنكسرة. في حالة الانحراف اللوني، ينكسر الضوء ذو الألوان المختلفة بكميات مختلفة قليلاً في العدسة. ونتيجة لذلك، يظهر قوس قزح حول الصورة وتظهر الصورة غير واضحة. في التلسكوب العاكس، تسقط أشعة الضوء من مصدر بعيد على سطح مرآة مقعرة مثبتة في الطرف السفلي من الأنبوب. استخدام المرآة بدلاً من العدسة يزيل الانحراف اللوني. تركز المرآة المقعرة الأشعة على مستواها البؤري. مشكلة التصميم هي كيفية مراقبة الصورة المركزة. استخدم نيوتن تصميمًا ينعكس فيه الضوء المركز من المرآة المقعرة على جانب واحد من الأنبوب في عدسة (الشكل\(\PageIndex{7a}\)). هذا الترتيب شائع في العديد من تلسكوبات الهواة ويسمى التصميم النيوتوني.
تعكس بعض التلسكوبات الضوء مرة أخرى باتجاه منتصف المرآة المقعرة باستخدام مرآة محدبة. في هذا الترتيب، تحتوي المرآة المقعرة التي تجمع الضوء على فتحة في المنتصف (\(\PageIndex{7b}\)). ثم يسقط الضوء على عدسة العدسة. هذا الترتيب للهدف والعدسة يسمى تصميم Cassegrain. معظم التلسكوبات الكبيرة، بما في ذلك تلسكوب هابل الفضائي، من هذا التصميم. الترتيبات الأخرى ممكنة أيضًا. في بعض التلسكوبات، يتم وضع كاشف الضوء مباشرة في المكان الذي يتم فيه تركيز الضوء بواسطة المرآة المنحنية.
معظم التلسكوبات البحثية الفلكية هي الآن من النوع العاكس. أحد أقدم التلسكوبات الكبيرة من هذا النوع هو تلسكوب هيل بحجم 200 بوصة (أو 5 أمتار) المبني على جبل بالومار في جنوب كاليفورنيا، والذي يحتوي على مرآة بقطر 200 بوصة. أحد أكبر التلسكوبات في العالم هو تلسكوب Keck الذي يبلغ طوله 10 أمتار في مرصد Keck على قمة بركان Mauna Kea الخامل في هاواي. يقوم مرصد كيك بتشغيل تلسكوبين بطول 10 أمتار. كل منها ليست مرآة واحدة، ولكنها تتكون بدلاً من ذلك من 36 مرآة سداسية. علاوة على ذلك، يمكن للتلسكوبين الموجودين على Keck العمل معًا، مما يزيد من قوتهما إلى مرآة فعالة يبلغ طولها 85 مترًا. تلسكوب هابل (الشكل\(\PageIndex{8}\)) هو تلسكوب عاكس كبير آخر مع مرآة أولية قطرها 2.4 متر. تم وضع هابل في مدار حول الأرض في عام 1990.

يتم أيضًا إعطاء التكبير الزاوي\(M\) للتلسكوب العاكس بواسطة المعادلة\ ref {eq2.36}. بالنسبة للمرآة الكروية، يكون البعد البؤري نصف قطر الانحناء، لذا فإن إنشاء مرآة موضوعية كبيرة لا يساعد التلسكوب على جمع المزيد من الضوء فحسب، بل يزيد أيضًا من تكبير الصورة.


