Skip to main content
Global

2.8: المكبر البسيط

  1. Last updated
  2. Save as PDF
  • Page ID
    196777

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • فهم بصريات المكبر البسيط
    • قم بتمييز الصورة التي تم إنشاؤها بواسطة مكبر بسيط

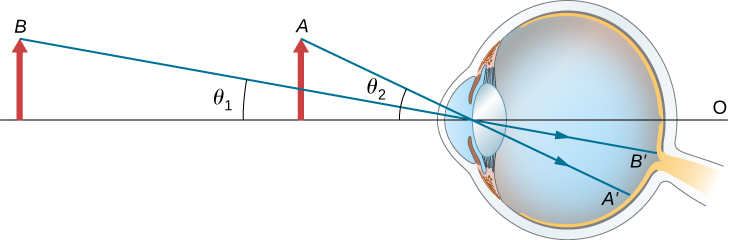
    يعتمد الحجم الظاهري للجسم الذي تدركه العين على الزاوية التي ينقلها الجسم من العين. كما هو موضح في الشكل\(\PageIndex{1}\)، فإن الكائن\(A\) عند النقطة يقترب من زاوية أكبر من العين منه عند موضعه عند النقطة\(B\). وبالتالي،\(A\) يشكل الكائن عند الصورة صورة أكبر على شبكية العين (انظر\(OA′\)) مما هو عليه عند وضعه في\(B\) (انظر\(OB′\)). وبالتالي، فإن الأجسام التي تقترب من زوايا كبيرة من العين تبدو أكبر لأنها تشكل صورًا أكبر على شبكية العين.

    يتم عرض كائنين من نفس الحجم أمام العين. الكائن A أقرب إلى العين ويشكل زاوية theta 2 مع المحور البصري. الكائن B أبعد ويشكل زاوية ثيتا 1 مع المحور البصري. داخل العين، تضرب الأشعة شبكية العين. يعتبر Ray B Prime أقرب إلى المحور البصري من الشعاع A Prime.
    الشكل\(\PageIndex{1}\): يتم تحديد الحجم الذي تدركه العين من خلال الزاوية الفرعية للكائن. تكون الصورة المتكونة على شبكية العين بواسطة كائن\(A\) بحجم أكبر من الصورة المتكونة على شبكية العين بواسطة نفس الكائن الموجود عند B (\(OA′\)مقارنة ارتفاعات الصورة بـ\(OB′\)).

    لقد رأينا أنه عندما يتم وضع كائن داخل البعد البؤري لعدسة محدبة، تكون صورته افتراضية ومستقيمة وأكبر من الكائن (انظر الجزء (ب) من هذا الشكل). وبالتالي، عندما تكون هذه الصورة التي تنتجها عدسة محدبة بمثابة كائن للعين، كما هو موضح في الشكل\(\PageIndex{2}\)، يتم تكبير الصورة على شبكية العين، لأن الصورة التي تنتجها العدسة تمثل زاوية أكبر في العين من الجسم. تسمى العدسة المحدبة المستخدمة لهذا الغرض العدسة المكبرة أو المكبر البسيط.

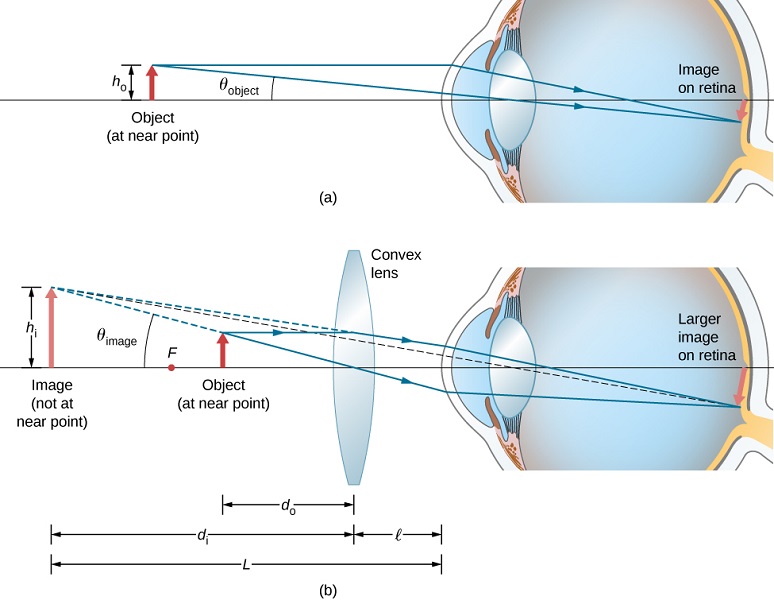
    يُظهر الشكل أ جسمًا بارتفاع h 0 أمام العين، عند النقطة القريبة. يتم تكوين صورة أصغر من الكائن على شبكية العين. يوضح الشكل (ب) عدسة ثنائية محدبة بين العين والجسم. تمر الأشعة من الجسم عبر هذا وتدخل العين لتكوين صورة أكبر على شبكية العين. تتلاقى الامتدادات الخلفية للأشعة المنحرفة بواسطة العدسة خلف الكائن لتشكل صورة أكبر من الكائن. مسافة هذه الصورة من العدسة هي d sopcept i ومسافة الكائن من العدسة هي d sopcept o. مسافة العدسة من العين هي l. مسافة الصورة من العين هي L. ارتفاع الصورة هو h sopcpt i.
    الشكل\(\PageIndex{2}\): المكبر البسيط عبارة عن عدسة محدبة تستخدم لإنتاج صورة مكبرة لجسم على شبكية العين. (أ) مع عدم وجود عدسة محدبة، يعرض الجسم زاوية\(θ_{object}\) من العين. (ب) عند وضع العدسة المحدبة في مكانها، تُظهر الصورة التي تنتجها العدسة المحدبة زاوية\(θ_{image}\) من العين، بمقدار\(θ_{image}> θ_{object}\). وبالتالي، تكون الصورة على شبكية العين أكبر مع وجود العدسة المحدبة في مكانها.

    لحساب تكبير العدسة المكبرة، نقارن الزاوية الفرعية بالصورة (التي تم إنشاؤها بواسطة العدسة) بالزاوية الفرعية للكائن (يتم عرضها بدون عدسة)، كما هو موضح في الشكل\(\PageIndex{1a}\). نفترض أن الجسم يقع في النقطة القريبة من العين، لأن هذه هي مسافة الجسم التي يمكن أن تشكل عندها العين غير المساعدة أكبر صورة على شبكية العين. سنقارن الصور المكبرة التي تم إنشاؤها بواسطة العدسة مع الحد الأقصى لحجم الصورة للعين بدون مساعدة. تكبير الصورة عندما تلاحظها العين هو التكبير الزاوي\(M\)، والذي يتم تحديده من خلال\(θ_{image}\) نسبة الزاوية الفرعية للصورة إلى\(θ_{object}\) الزاوية الفرعية للكائن:

    \[M=\dfrac{θ_{image}}{θ_{object}}. \nonumber \]

    ضع في اعتبارك الموقف الموضح في الشكل\(\PageIndex{1b}\). يتم وضع العدسة المكبرة على مسافة\(ℓ\) من العين، وتشكل الصورة التي ينتجها المكبر مسافة\(L\) من العين. نريد حساب التكبير الزاوي لأي عشوائي\(L\) و\(ℓ\). في التقريب ذي الزاوية الصغيرة، يكون الحجم\(θ_{image}\) الزاوي للصورة\(h_i/L\). الحجم الزاوي\(θ_{object}\) للكائن عند النقطة القريبة هو\(θ_{object}=h_o/25\,cm\). ثم يتم التكبير الزاوي

    \[\underbrace{ M=\dfrac{θ_{image}}{θ_{object}}=\dfrac{h_i(25cm)}{Lh_o}}_{\text{angular magnification}} . \label{angular magnification} \]

    استخدام تعريف التكبير الخطي

    \[m=−\dfrac{d_i}{d_o}=\dfrac{h_i}{h_o} \label{mag} \]

    ومعادلة العدسة الرقيقة

    \[\dfrac{1}{d_o}+\dfrac{1}{d_i}=\dfrac{1}{f} \nonumber \]

    نصل إلى التعبير التالي للتكبير الزاوي للعدسة المكبرة:

    \[\begin{align} M&= \left(−\dfrac{d_i}{d_o}\right)\left(\dfrac{25\,cm}{L}\right) \\[4pt] &=−d_i\left(\dfrac{1}{f}−\dfrac{1}{d_i}\right)\left(\dfrac{25\,cm}{L}\right) \\[4pt] &= \left(1−\dfrac{d_i}{f}\right)\left(\dfrac{25\,cm}{L}\right) \label{eq10} \end{align} \]

    من الشكل\(\PageIndex{1b}\)، نرى أن القيمة المطلقة لمسافة الصورة هي\(|d_i|=L−ℓ\). لاحظ أنه\(d_i<0\) نظرًا لأن الصورة افتراضية، يمكننا الاستغناء عن القيمة المطلقة عن طريق إدراج علامة الطرح بشكل صريح:

    \[−d_i=L−ℓ. \label{eq34} \]

    يعطينا إدراج المعادلة\ ref {eq34} في المعادلة\ ref {eq10} المعادلة النهائية للتكبير الزاوي للعدسة المكبرة:

    \[M=\left(\dfrac{25\,cm}{L}\right) \left(1+\dfrac{L−ℓ}{f} \right). \label{eq12} \]

    لاحظ أنه يجب التعبير عن جميع الكميات في هذه المعادلة بالسنتيمترات. غالبًا ما نريد أن تكون الصورة على مسافة قريبة (على سبيل المثال،\(L=25\,cm\)) للحصول على أقصى قدر من التكبير، ونحمل العدسة المكبرة بالقرب من العين (\(ℓ=0\)). في هذه الحالة، تعطي المعادلة\ ref {eq12}

    \[M=1+\dfrac{25\,cm}{f} \label{eq13} \]

    مما يدل على أن التكبير الأكبر يحدث للعدسة ذات البعد البؤري الأقصر. بالإضافة إلى ذلك، عندما تكون الصورة على مسافة قريبة من النقطة ويتم تثبيت العدسة بالقرب من العين (\(ℓ=0\))، تصبح المعادلة\ ref {eq12}\(L=d_i=25\,cm\)

    \[M=\dfrac{h_i}{h_o}=m \label{eq14} \]

    \(m\)أين التكبير الخطي (المعادلة\ ref {mag}) المشتق سابقًا للمرايا الكروية والعدسات الرقيقة. موقف مفيد آخر هو عندما تكون الصورة في اللانهاية (\(L=\infty\)). ثم تأخذ المعادلة\ ref {eq12} الشكل

    \[M(L=\infty)=\dfrac{25\,cm}{f}. \label{eq15} \]

    التكبير الناتج هو ببساطة نسبة المسافة القريبة من النقطة إلى الطول البؤري للعدسة المكبرة، لذا فإن العدسة ذات البعد البؤري الأقصر تعطي تكبيرًا أقوى. على الرغم من أن نسبة التكبير هذه أصغر بمقدار 1 من نسبة التكبير التي تم الحصول عليها مع الصورة عند النقطة القريبة، إلا أنها توفر ظروف المشاهدة الأكثر راحة، لأن العين تكون مسترخية عند عرض كائن بعيد.

    بمقارنة المعادلات\ ref {eq13} و\ ref {eq15}، نرى أن نطاق التكبير الزاوي لعدسة متقاربة معينة هو

    \[\dfrac{25cm}{f} ≤ M ≤1+\dfrac{25cm}{f}. \nonumber \]

    مثال\(\PageIndex{1}\): Magnifying a Diamond

    يرغب صائغ في فحص ماسة قطرها 3.0 مم باستخدام مكبر. يتم تثبيت الماس عند النقطة القريبة من الصائغ (25 سم)، ويحمل الصائغ العدسة المكبرة بالقرب من عينه.

    1. ماذا يجب أن يكون البعد البؤري للعدسة المكبرة لرؤية صورة قطرها 15 مم للماس؟
    2. ماذا يجب أن يكون الطول البؤري للعدسة المكبرة للحصول على نسبة تكبير 10 ×؟

    إستراتيجية

    نحن بحاجة إلى تحديد التكبير المطلوب للمكبر. نظرًا لأن الصائغ يحمل العدسة المكبرة بالقرب من عينه، يمكننا استخدام Equation\ ref {eq13} للعثور على البعد البؤري للعدسة المكبرة.

    الحل

    أ. التكبير الخطي المطلوب هو نسبة قطر الصورة المطلوبة إلى القطر الفعلي للماس (المعادلة\ ref {eq15}). نظرًا لأن الصائغ يحمل العدسة المكبرة بالقرب من عينه وتتشكل الصورة عند النقطة القريبة منه، فإن التكبير الخطي هو نفس التكبير الزاوي، لذلك

    \[\begin{align*} M &=m=\dfrac{h_i}{h_o}\\[4pt] &=\dfrac{15\,mm}{3.0\,mm} \\[4pt] &=5.0.\end{align*} \nonumber \]

    يمكن حساب الطول البؤري f للعدسة المكبرة عن طريق حل المعادلة\ ref {eq13} لـ\(f\)، والتي تعطي

    \[M=1+\dfrac{25\,cm}{f} \nonumber \]

    \[\begin{align*} f&=\dfrac{25\,cm}{M−1} \\[4pt] &= \dfrac{25\,cm}{5.0−1} \\[4pt] &= 6.3\,cm \end{align*} \nonumber \]

    ب. لتكبير الصورة بعامل عشرة، نقوم مرة أخرى بحل المعادلة\ ref {eq13} لـ\(f\)، ولكن هذه المرة نستخدمها\(M=10\). النتيجة هي

    \[\begin{align*} f &=\dfrac{25\,cm}{M−1} \\[4pt] &=\dfrac{25\,cm}{10−1} \\[4pt] &=2.8\,cm. \end{align*} \nonumber \]

    الدلالة

    لاحظ أنه يتم تحقيق تكبير أكبر باستخدام عدسة ذات طول بؤري أصغر. لذلك نحتاج إلى استخدام عدسة بنصف قطر انحناء أقل من بضعة سنتيمترات وإبقائها قريبة جدًا من أعيننا. هذا ليس مريحًا جدًا. يمكن للمجهر المركب، الذي تم استكشافه في القسم التالي، التغلب على هذا العيب.