2.5: عدسات رقيقة

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

• استخدم مخططات الأشعة لتحديد ووصف الصورة المشكلة بواسطة عدسة.
• استخدم معادلة العدسة الرقيقة لوصف وتحديد موقع الصورة المشكلة بواسطة عدسة

توجد العدسات في مجموعة كبيرة من الأدوات البصرية، بدءًا من العدسة المكبرة البسيطة إلى عدسة التكبير الخاصة بالكاميرا إلى العين نفسها. في هذا القسم، نستخدم قانون Snell لاستكشاف خصائص العدسات وكيفية تكوين الصور.

كلمة «عدسة» مشتقة من الكلمة اللاتينية لفول العدس، الذي يشبه شكله عدسة محدبة. ومع ذلك، لا تحتوي جميع العدسات على نفس الشكل. \(\PageIndex{1}\)يوضح الشكل مجموعة متنوعة من أشكال العدسات المختلفة. المفردات المستخدمة لوصف العدسات هي نفسها المستخدمة في المرايا الكروية: يسمى محور التماثل للعدسة بالمحور البصري، حيث يتقاطع هذا المحور، سطح العدسة يسمى قمة العدسة، وهكذا دواليك.

الشكل\(\PageIndex{1}\): أنواع مختلفة من العدسات: لاحظ أن العدسة المتقاربة لها «خصر» أكثر سمكًا، في حين أن العدسة المتباينة لها خصر أرق.

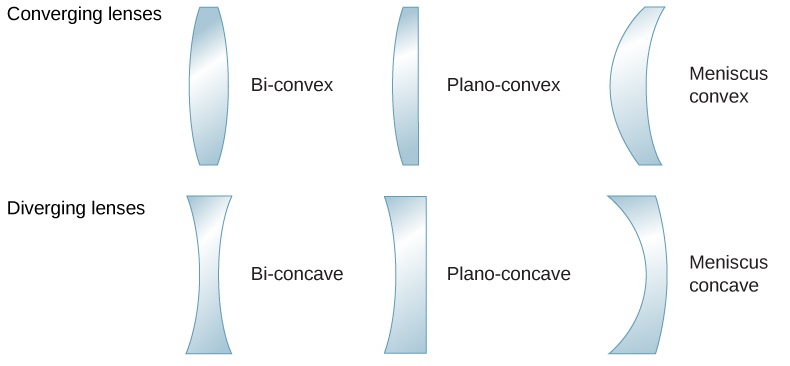
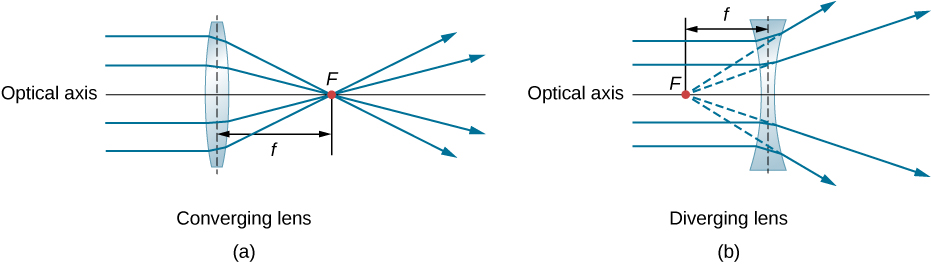
يتم تشكيل العدسة المحدبة أو المتقاربة بحيث تتقاطع جميع أشعة الضوء التي تدخلها بالتوازي مع محورها البصري (أو تركيزها) عند نقطة واحدة على المحور البصري على الجانب الآخر من العدسة، كما هو موضح في الشكل\(\PageIndex{1a}\). وبالمثل، يتم تشكيل عدسة مقعرة أو متباينة بحيث تتباعد جميع الأشعة التي تدخلها بالتوازي مع محورها البصري، كما هو موضح في الجزء (ب). لفهم كيفية معالجة العدسة للضوء بدقة أكبر، انظر عن كثب إلى الشعاع العلوي الذي يمر عبر العدسة المتقاربة في الجزء (أ). نظرًا لأن معامل انكسار العدسة أكبر من معامل انكسار الهواء، فإن قانون سنيل يخبرنا أن الشعاع ينحني نحو العمودي على الواجهة عند دخوله العدسة. وبالمثل، عندما يخرج الشعاع من العدسة، فإنه ينحني بعيدًا عن العمودي. وينطبق نفس المنطق على العدسات المتباينة، كما هو موضح في الشكل \(\PageIndex{1b}\). التأثير العام هو أن أشعة الضوء تنحني نحو المحور البصري للعدسة المتقاربة وبعيدًا عن المحور البصري للعدسات المتباينة. بالنسبة للعدسة المتقاربة، فإن النقطة التي تتقاطع عندها الأشعة هي النقطة البؤرية F للعدسة. بالنسبة للعدسة المتباينة، فإن النقطة التي يبدو أن الأشعة تنشأ منها هي النقطة البؤرية (الافتراضية). المسافة من مركز العدسة إلى النقطة البؤرية هي البعد البؤري f للعدسة.

الشكل\(\PageIndex{2}\): تتقارب أشعة الضوء الداخلة إلى (أ) عدسة متقاربة و (ب) عدسة متباينة، موازية لمحورها، عند النقطة البؤرية F. المسافة من مركز العدسة إلى النقطة البؤرية هي البعد البؤري للعدسة f. لاحظ أن أشعة الضوء تنحني عند الدخول والخروج من العدسة، مع التأثير العام المتمثل في ثني الأشعة باتجاه المحور البصري.

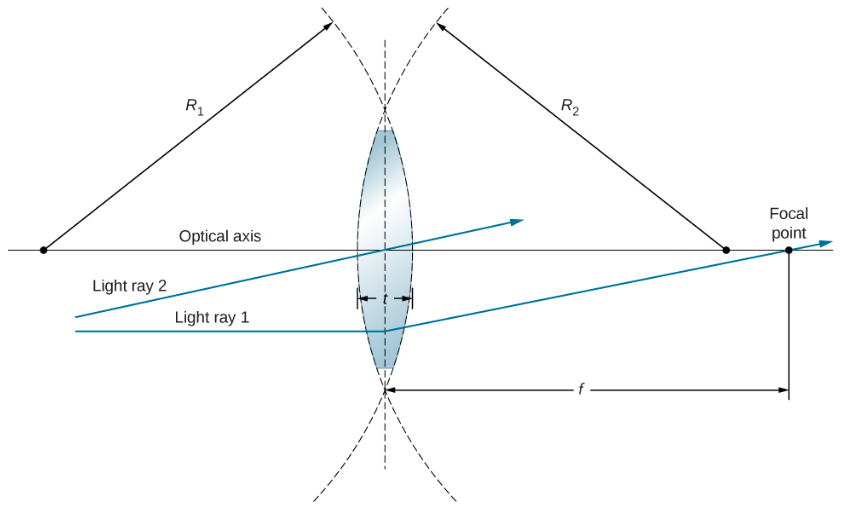
تعتبر العدسة رقيقة إذا كان سمكها أقل بكثير من نصف قطر انحناء كلا السطحين، كما هو موضح في الشكل\(\PageIndex{3}\). في هذه الحالة، يمكن اعتبار الأشعة وكأنها تنحني مرة واحدة في مركز العدسة. بالنسبة إلى الحالة المرسومة في الشكل، يكون شعاع الضوء 1 موازيًا للمحور البصري، لذلك ينحني الشعاع الصادر مرة واحدة في مركز العدسة ويمر عبر النقطة البؤرية. من الخصائص المهمة الأخرى للعدسات الرقيقة أن أشعة الضوء التي تمر عبر مركز العدسة غير منحرفة، كما هو موضح في شعاع الضوء 2.

الشكل\(\PageIndex{3}\): في تقريب العدسة الرقيقة، يكون سمك t للعدسة أقل بكثير من نصف قطر R ₁ و R ₂ لانحناء أسطح العدسة. يُنظر إلى الأشعة الضوئية على أنها تنحني في مركز العدسة، مثل شعاع الضوء 1. يمر شعاع الضوء 2 عبر مركز العدسة ولا ينحرف في تقريب العدسة الرقيقة.

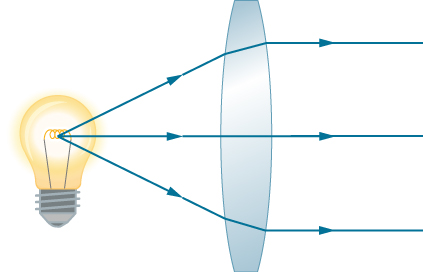
كما لوحظ في المناقشة الأولية لقانون سنيل، فإن مسارات أشعة الضوء يمكن عكسها تمامًا. هذا يعني أنه يمكن عكس اتجاه الأسهم لجميع الأشعة في الشكل \(\PageIndex{2}\). على سبيل المثال، إذا تم وضع مصدر ضوء نقطي في النقطة البؤرية لعدسة محدبة، كما هو موضح في الشكل \(\PageIndex{4}\)، فإن أشعة الضوء المتوازية تظهر من الجانب الآخر.

الشكل\(\PageIndex{4}\) في العدسات المتقاربة والمتباينة. تُستخدم هذه التقنية في المنارات وأحيانًا في إشارات المرور لإنتاج شعاع ضوئي اتجاهي من مصدر يصدر الضوء في جميع الاتجاهات.

تتبع الأشعة والعدسات الرقيقة

تتبع الأشعة هو أسلوب تحديد أو متابعة (تتبع) المسارات التي تسلكها أشعة الضوء. تتبع الأشعة للعدسات الرقيقة مشابه جدًا للتقنية التي استخدمناها مع المرايا الكروية. أما بالنسبة للمرايا، فإن تتبع الأشعة يمكن أن يصف بدقة تشغيل العدسة. تتشابه قواعد تتبع الأشعة للعدسات الرقيقة مع تلك الخاصة بالمرايا الكروية:

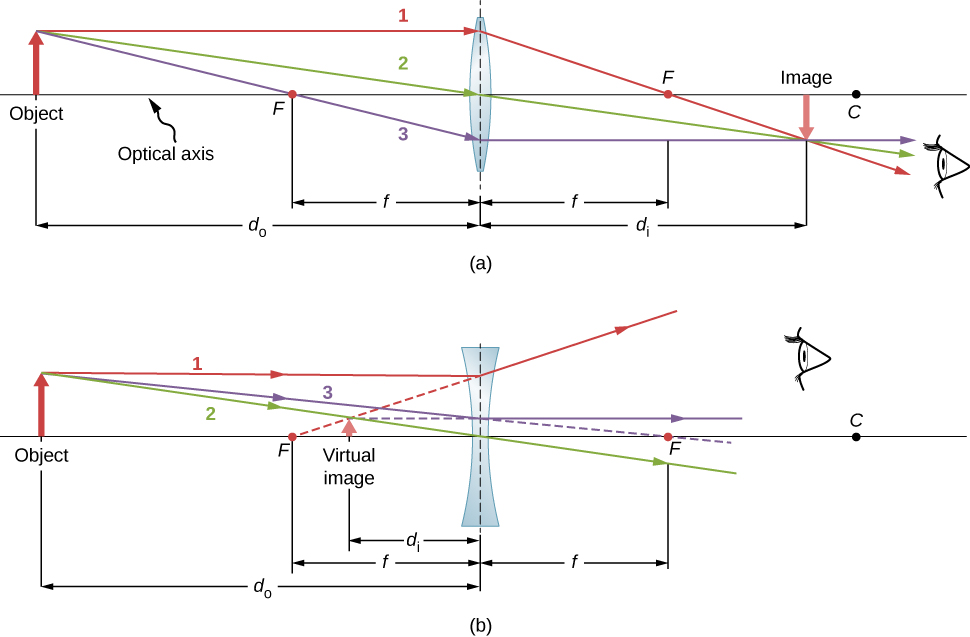
1. يمر الشعاع الذي يدخل عدسة متقاربة موازية للمحور البصري عبر النقطة البؤرية على الجانب الآخر من العدسة (الشعاع 1 في الجزء (أ) من الشكل\(\PageIndex{4}\)). يخرج الشعاع الذي يدخل عدسة متباينة موازية للمحور البصري على طول الخط الذي يمر عبر النقطة البؤرية على نفس جانب العدسة (الشعاع 1 في الجزء (ب) من الشكل).
2. لا ينحرف الشعاع الذي يمر عبر مركز عدسة متقاربة أو متباينة (الشعاع 2 في الجزئين (أ) و (ب)).
3. بالنسبة للعدسة المتقاربة، يخرج الشعاع الذي يمر عبر النقطة البؤرية من العدسة بالتوازي مع المحور البصري (الشعاع 3 في الجزء (أ)). بالنسبة للعدسة المتباينة، يخرج الشعاع الذي يقترب على طول الخط الذي يمر عبر النقطة البؤرية على الجانب المقابل من العدسة الموازية للمحور (الشعاع 3 في الجزء (ب)).

الشكل\(\PageIndex{5}\): العدسات الرقيقة لها نفس الأطوال البؤرية على كلا الجانبين. (أ) أشعة ضوئية متوازية تدخل عدسة متقاربة من التقاطع الأيمن عند النقطة البؤرية على اليسار. (ب) يبدو أن أشعة الضوء الموازية التي تدخل عدسة متباينة من اليمين تأتي من النقطة المحورية على اليمين.

تعمل العدسات الرقيقة جيدًا للضوء أحادي اللون (أي الضوء ذي الطول الموجي الواحد). ومع ذلك، بالنسبة للضوء الذي يحتوي على عدة أطوال موجية (مثل الضوء الأبيض)، تعمل العدسات بشكل أقل جودة. تكمن المشكلة، كما تعلمنا في الفصل السابق، في أن معامل انكسار المادة يعتمد على الطول الموجي للضوء. هذه الظاهرة مسؤولة عن العديد من التأثيرات الملونة، مثل قوس قزح. لسوء الحظ، تؤدي هذه الظاهرة أيضًا إلى انحرافات في الصور التي تشكلها العدسات. على وجه الخصوص، نظرًا لأن المسافة البؤرية للعدسة تعتمد على معامل الانكسار، فإنها تعتمد أيضًا على الطول الموجي للضوء الساقط. وهذا يعني أن الضوء ذي الأطوال الموجية المختلفة سيركز على نقاط مختلفة، مما ينتج عنه ما يسمى بـ «الانحرافات اللونية». على وجه الخصوص، ستصبح حواف صورة كائن أبيض ملونة وغير واضحة. العدسات الخاصة التي تسمى العدسات المزدوجة قادرة على تصحيح الانحرافات اللونية. يتم تشكيل العدسة المزدوجة عن طريق لصق عدسة متقاربة وعدسة متباينة. تنتج العدسة المزدوجة المدمجة انحرافات لونية منخفضة بشكل كبير.

تكوين الصورة بواسطة عدسات رقيقة

نحن نستخدم تتبع الأشعة لفحص أنواع مختلفة من الصور التي يمكن إنشاؤها بواسطة عدسة. في بعض الحالات، تشكل العدسة صورة حقيقية، مثل عندما يقوم جهاز عرض فيلم بإلقاء صورة على الشاشة. في حالات أخرى، تكون الصورة عبارة عن صورة افتراضية لا يمكن عرضها على الشاشة. أين، على سبيل المثال، يتم تشكيل الصورة بواسطة النظارات؟ نستخدم تتبع الأشعة للعدسات الرقيقة لتوضيح كيفية تكوين الصور، ثم نقوم بتطوير المعادلات لتحليل خصائص العدسات الرقيقة كميًا.

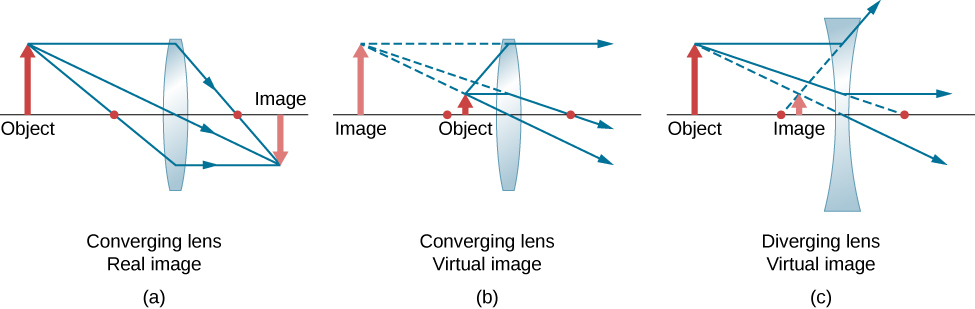
ضع في اعتبارك كائنًا على بعد مسافة من العدسة المتقاربة، كما هو موضح في الشكل\(\PageIndex{6}\). للعثور على موقع وحجم الصورة، نتتبع مسارات أشعة الضوء المحددة التي تنشأ من نقطة واحدة على الكائن، وفي هذه الحالة، طرف السهم. يوضِّح الشكل ثلاثة أشعة من العديد من الأشعة المنبعثة من طرف السهم. يمكن تتبع هذه الأشعة الثلاثة باستخدام قواعد تتبع الأشعة المذكورة أعلاه.

• يدخل الشعاع 1 العدسة بالتوازي مع المحور البصري ويمر عبر النقطة البؤرية على الجانب الآخر (القاعدة 1).
• يمر الشعاع 2 عبر مركز العدسة ولا ينحرف (القاعدة 2).
• يمر الشعاع 3 عبر النقطة البؤرية في طريقه إلى العدسة ويخرج من العدسة بالتوازي مع المحور البصري (القاعدة 3).

تتقاطع الأشعة الثلاثة عند نقطة واحدة على الجانب الآخر من العدسة. وبالتالي، توجد صورة طرف السهم في هذه المرحلة. تنكسر جميع الأشعة التي تأتي من طرف السهم وتدخل العدسة وتتقاطع عند النقطة الموضحة.

بعد تحديد موقع صورة طرف السهم، نحتاج إلى نقطة أخرى من الصورة لتوجيه صورة السهم بأكملها. لقد اخترنا تحديد موقع قاعدة صورة السهم الموجود على المحور البصري. كما هو موضح في القسم الخاص بالمرايا الكروية، ستكون القاعدة على المحور البصري فوق صورة طرف السهم مباشرةً (بسبب التماثل العلوي والسفلي للعدسة). وبالتالي، تمتد الصورة عبر المحور البصري إلى الارتفاع (السلبي) الموضح. تتقاطع الأشعة من نقطة أخرى على السهم، مثل منتصف السهم، عند نقطة مشتركة أخرى، وبالتالي تملأ بقية الصورة.

على الرغم من تتبع ثلاثة أشعة في هذا الشكل، إلا أنه يلزم وجود شعاعين فقط لتحديد نقطة من الصورة. من الأفضل تتبع الأشعة التي توجد لها قواعد بسيطة لتتبع الأشعة.

الشكل\(\PageIndex{6}\): يُستخدم تتبع الأشعة لتحديد موقع الصورة المشكلة بواسطة عدسة. يتم تتبع الأشعة الصادرة من نفس النقطة على الجسم - تتبع الأشعة الثلاثة المختارة واحدة من قواعد تتبع الأشعة، بحيث يسهل تحديد مساراتها. توجد الصورة عند النقطة التي تتقاطع فيها الأشعة. في هذه الحالة، يتم تشكيل صورة حقيقية - صورة يمكن عرضها على الشاشة.

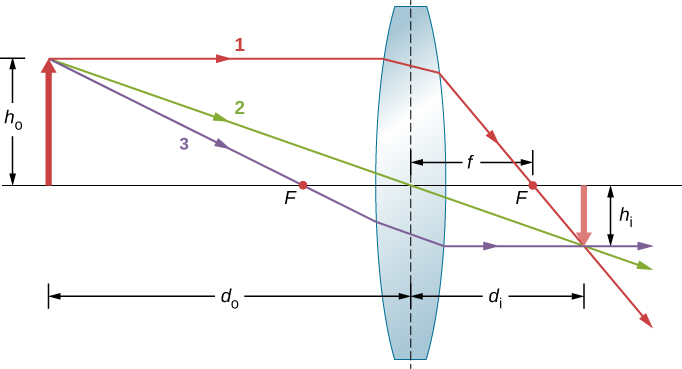
تظهر عدة مسافات مهمة في الشكل. أما بالنسبة للمرآة، فنحن نُعرِّف الدودو على أنه مسافة الكائن، أو مسافة الجسم من مركز العدسة. تُعرّف مسافة الصورة d _i بأنها مسافة الصورة من مركز العدسة. يشار إلى ارتفاع الكائن وارتفاع الصورة بـ h _o و h _i، على التوالي. الصور التي تظهر بشكل مستقيم بالنسبة للكائن لها ارتفاعات موجبة، وتلك المقلوبة لها ارتفاعات سالبة. باستخدام قواعد تتبع الأشعة وعمل رسم بمقياس باستخدام الورق والقلم الرصاص، كما هو الحال في الشكل \(\PageIndex{6}\)، يمكننا وصف موقع الصورة وحجمها بدقة. لكن الفائدة الحقيقية لتتبع الأشعة تكمن في تصور كيفية تكوين الصور في مجموعة متنوعة من المواقف.

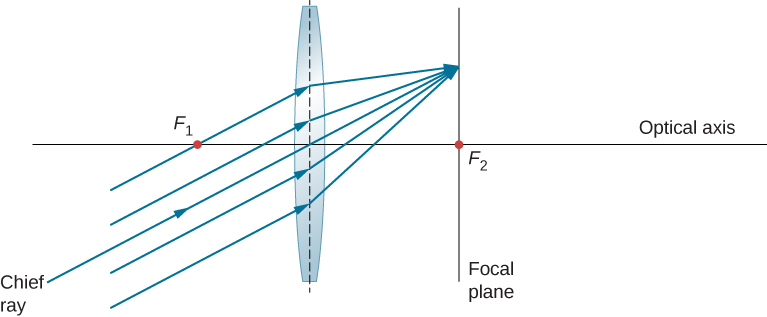
الأشعة المتوازية المائلة والمستوى البؤري

لقد رأينا أن الأشعة الموازية للمحور البصري موجهة إلى النقطة البؤرية للعدسة المتقاربة. في حالة اختلاف العدسة، فإنها تخرج في اتجاه يبدو أنها قادمة من النقطة البؤرية على الجانب الآخر من العدسة (أي الجانب الذي تدخل منه الأشعة المتوازية العدسة). ماذا يحدث للأشعة المتوازية غير الموازية للمحور البصري (الشكل \(\PageIndex{7}\))؟ في حالة العدسة المتقاربة، لا تتقارب هذه الأشعة عند النقطة المحورية. بدلاً من ذلك، يجتمعون في نقطة أخرى في الطائرة تسمى المستوى البؤري. يحتوي المستوى البؤري على النقطة البؤرية وهو عمودي على المحور البصري. كما هو موضح في الشكل، تركز الأشعة المتوازية حيث يعبر الشعاع عبر مركز العدسة المستوى البؤري.

الشكل\(\PageIndex{7}\): تركز الأشعة المائلة المتوازية على نقطة في المستوى البؤري.

معادلة العدسة الرقيقة

يتيح لنا تتبع الأشعة الحصول على صورة نوعية لتشكيل الصورة. للحصول على معلومات رقمية، نستمد زوجًا من المعادلات من التحليل الهندسي لتتبع الأشعة للعدسات الرقيقة. تسمح لنا هذه المعادلات، التي تسمى معادلة العدسة الرقيقة ومعادلة صانع العدسات، بالتحليل الكمي للعدسات الرقيقة.

ضع في اعتبارك العدسة السميكة ثنائية المحدبة الموضحة في الشكل \(\PageIndex{8}\). معامل انكسار الوسط المحيط هو n ₁ (إذا كانت العدسة في الهواء، إذن\(n_1=1.00\)) ومعامل انكسار العدسة هو\(n_2\). أنصاف أقطار الانحناءات على الجانبين هي\(R_1\) الرمال\(R_2\). نرغب في إيجاد علاقة بين مسافة\(d_o\) الكائن ومسافة الصورة\(d_i\) ومعلمات العدسة.

الشكل الذي\(\PageIndex{8}\) يُستخدم لاشتقاق معادلة صانع العدسات. هنا،\(t\) هو سمك العدسة، n ₁ هو مؤشر انكسار الوسط الخارجي،\(n_2\) وهو مؤشر انكسار العدسة. نحن نأخذ الحد الأقصى\(t→0\) للحصول على صيغة عدسة رقيقة.

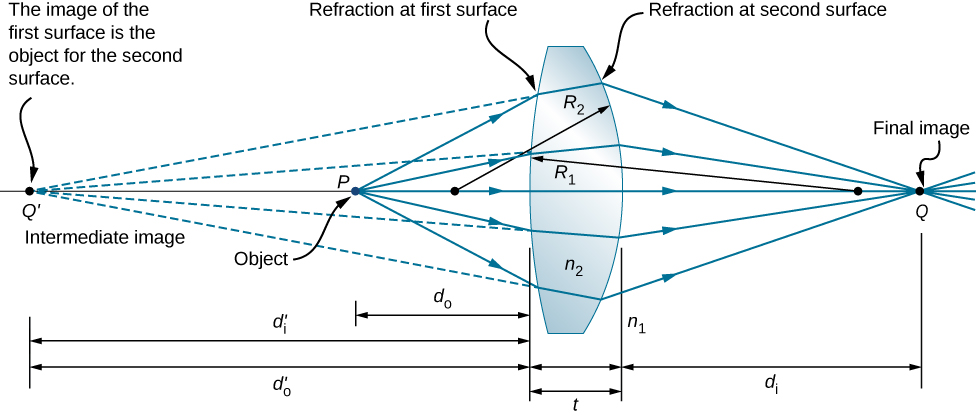
لاشتقاق معادلة العدسة الرقيقة، نأخذ في الاعتبار الصورة التي تكونت من السطح المنكسر الأول (أي السطح الأيسر) ثم نستخدم هذه الصورة ككائن لسطح الانكسار الثاني. في الشكل، الصورة من السطح الانكساري الأول هي\(Q′\) التي تتكون من تمديد الأشعة من داخل العدسة إلى الخلف (تنتج هذه الأشعة عن الانكسار عند السطح الأول). يظهر ذلك من خلال الخطوط المتقطعة في الشكل. لاحظ أن هذه الصورة افتراضية لأنه لا توجد أشعة تمر فعليًا عبر النقطة Q′. للعثور على مسافة الصورة\(d′_i\) المقابلة للصورة Q′، نستخدم المعادلة 2.4.9. في هذه الحالة\(d_o\)، تكون مسافة الكائن هي مسافة الصورة d′idi′، ونصف قطر الانحناء هو\(R_1\). يؤدي إدخال هذه العناصر في العلاقة المشتقة سابقًا للانكسار عند أسطح المنحنيات إلى

\ [\ dfrac {n_1} {d_o} +\ dfrac {n_2} {d′_i} =\ dfrac {n_2−n_1} {R_1}. \ التسمية {51}\]

_{الصورة افتراضية وعلى نفس جانب الكائن، لذا قم بذلك <0 و d o >0.} السطح الأول محدب تجاه الكائن، لذلك\(R_1>0\).

للعثور على مسافة الجسم للجسم\(Q\) المتكون من الانكسار من الواجهة الثانية، لاحظ أن دور مؤشري الانكسار n ₁ و n _{2 متبادلان} في المعادلة 2.4.9. في الشكل\(\PageIndex{8}\)، تنشأ الأشعة في الوسط مع الفهرس\(n_2\)، بينما في الشكل 2.4.3، تنشأ الأشعة في الوسط مع الفهرس \(n_1\). وبالتالي، يجب علينا تبادل n ₁ و n ₂ في المعادلة 2.4.9. بالإضافة إلى ذلك، من خلال الرجوع إلى الشكل مرة أخرى\(\PageIndex{8}\)، نرى أن مسافة الكائن هي\(d′_o\) ومسافة الصورة هي \(d_i\). نصف قطر الانحناء هو R _{2 عند} إدخال هذه الكميات في المعادلة 2.4.9 يعطي

\ [\ dfrac {n_2} {d′_o} +\ dfrac {n_1} {d_i} =\ dfrac {n_1−n_2} {R_2}. \ التسمية {eq51}\]

الصورة حقيقية وعلى الجانب الآخر من الكائن، لذلك \(d_i>0\) و\(d_o′>0\). السطح الثاني محدب بعيدًا عن الكائن، لذا\(R_2<0\). يمكن تبسيط المعادلة\ ref {eq51} من خلال ملاحظة ذلك

\[d′_o=|d′_i|+t, \nonumber \]

حيث أخذنا القيمة المطلقة لأنها\(d′_i\) رقم سالب، في حين أن\(t\) كلاهما\(d′_o\) موجب. يمكننا الاستغناء عن القيمة المطلقة إذا رفضنا\(d′_i\)، مما يعطي

\[ d′_o=−d′_i+td. \nonumber \]

إدراج هذا في المعادلة\ ref {eq51} يعطي

\ [\ dfrac {n_2} {−d′_i+t} +\ dfrac {n_1} {d_i} =\ dfrac {n_1−n_2} {R_2}. \ التسمية {eq52}\]

يعطي مجموع المعادلات\ ref {eq51} و\ ref {eq52}

\ [\ dfrac {n_1} {d_o} +\ dfrac {n_1} {d_i} +\ dfrac {n_2} {d′_i} +\ dfrac {n_2} {n_2} {−i+t} = (n_2−n_1) \ يسار (\ dfrac {1} {r_1} -\ dfrac {n_1} -\ dfrac {n_1} c {1} {R_2}\ اليمين). \ التسمية {eq54}\]

في عملية تقريب العدسة الرقيقة، نفترض أن العدسة رقيقة جدًا مقارنة بمسافة الصورة الأولى، أو\(t \ll d′_i\) (أو، بشكل مكافئ،\(t \ll R_1\) و\(t \ll R_2\)). في هذه الحالة، يتم إلغاء المصطلحين الثالث والرابع على الجانب الأيسر من المعادلة\ ref {eq54}، تاركين لنا

\ [\ dfrac {n_1} {d_o} +\ dfrac {n_1} {d_i} = (n_2−n_1) \ يسار (\ dfrac {1} {R_1} −\ dfrac {1} {1} {R_2}\ يمين). \ لا يوجد رقم\]

القسمة على\(n_1\) الوجه تعطينا أخيرًا

\ [\ dfrac {1} {d_o} +\ dfrac {1} {d_i} =\ يسار (\ dfrac {n_2} {n_2} {n_1} −1 \ يمين)\ يسار (\ dfrac {1} −\ dfrac {1}\ dfrac {1}\ dfrac {1}\ يمين). \ التسمية {eq58}\]

يبدو الجانب الأيسر بشكل مثير للريبة مثل معادلة المرآة التي اشتقناها أعلاه للمرايا الكروية. كما هو الحال بالنسبة للمرايا الكروية، يمكننا استخدام تتبع الأشعة والهندسة لإظهار أنه بالنسبة للعدسة الرقيقة،

\ [ \ underbrace {\ dfrac {1} {d_o} +\ dfrac {1} {d_i} =\ dfrac {1} {f}} _ { \ text {معادلة العدسة الرقيقة}}\ التسمية {معادلة العدسة الرقيقة}\]

أين\(f\) هو البعد البؤري للعدسة الرقيقة (يُترك هذا الاشتقاق كتمرين). هذه هي معادلة العدسة الرقيقة. الطول البؤري للعدسة الرقيقة هو نفسه على يسار ويمين العدسة. الجمع بين المعادلات \ ref {معادلة العدسة الرقيقة} و\ ref {eq58} يعطي

\ [\ underbrace {\ dfrac {1} {f} =\ يسار (\ dfrac {n_2} {n_1} −1} −1 \ يمين)\ يسار (\ dfrac {1} −\ dfrac {1}\ dfrac {1} {R_2}\\ يمين)} _ {\\ نص { معادلة صانع العدسات}}\ التسمية {صانع العدسات}\]

وهو ما يسمى معادلة صانع العدسات. يُظهر أن الطول البؤري للعدسة الرقيقة يعتمد فقط على نصف قطر الانحناء ومعامل انكسار العدسة والوسيط المحيط. للعدسة في الهواء\(n_2≡n\)،\(n_1=1.0\) وبالتالي تنخفض معادلة صانع العدسات إلى

\ [\ dfrac {1} {f} = (n−1) \ يسار (\ dfrac {1} {R_1} −\ dfrac {1} {R_2}\ يمين). \ لا يوجد رقم\]

اتفاقيات التوقيع للعدسات

لاستخدام معادلة العدسة الرقيقة بشكل صحيح، يجب الامتثال لاتفاقيات العلامات التالية:

• \(d_i\)يكون موجبًا إذا كانت الصورة على الجانب المقابل للكائن (أي الصورة الحقيقية)؛ وإلا\(d_i\) تكون سلبية (أي الصورة الافتراضية).
• \(f\)إيجابي للعدسة المتقاربة وسالب للعدسة المتباينة.
• \(R\)يكون موجبًا للسطح المحدب تجاه الجسم، وسالبًا لسطح مقعر باتجاه الجسم.

التكبير

باستخدام كائن بحجم محدود على المحور البصري وتتبع الأشعة، يمكنك إظهار أن تكبير\(m\) الصورة هو

\[m \equiv \dfrac{h_i}{h_o}=−\dfrac{d_i}{d_o} \label{mag} \]

(حيث تعني الأسطر الثلاثة «يتم تعريفها على أنها»). هذه هي بالضبط نفس المعادلة التي حصلنا عليها للمرايا (انظر المعادلة 2.3.15). إذا كان\(m>0\) للصورة نفس الاتجاه الرأسي للكائن (تسمى الصورة «المستقيمة»). إذا كانت m<0، فإن الصورة لها الاتجاه الرأسي المعاكس ككائن (تسمى الصورة «المقلوبة»).

استخدام معادلة العدسة الرقيقة

تنطبق معادلة العدسة الرقيقة ومعادلة صانع العدسات على نطاق واسع في الحالات التي تنطوي على عدسات رقيقة. نستكشف العديد من ميزات تكوين الصور في الأمثلة التالية.

ضع في اعتبارك عدسة متقاربة رقيقة. أين تتشكل الصورة وما نوع الصورة التي تتكون عندما يقترب الجسم من العدسة من اللانهاية؟ يمكن ملاحظة ذلك باستخدام معادلة العدسة الرقيقة لطول بؤري معين لرسم مسافة الصورة كدالة لمسافة الكائن. وبعبارة أخرى، نحن نرسم

\[d_i=\left(\dfrac{1}{f}−\dfrac{1}{d_o}\right)^{−1} \nonumber \]

للحصول على قيمة معينة من\(f\). بالنسبة إلى ذلك\(f=1\,cm\)، تظهر النتيجة في الشكل\(\PageIndex{9a}\).

الشكل\(\PageIndex{9}\): (أ) مسافة الصورة لعدسة متقاربة رقيقة ذات f=1.0 سم كدالة لمسافة الكائن. (ب) نفس الشيء ولكن بالنسبة لعدسة متباينة ذات f=−1.0 سم.

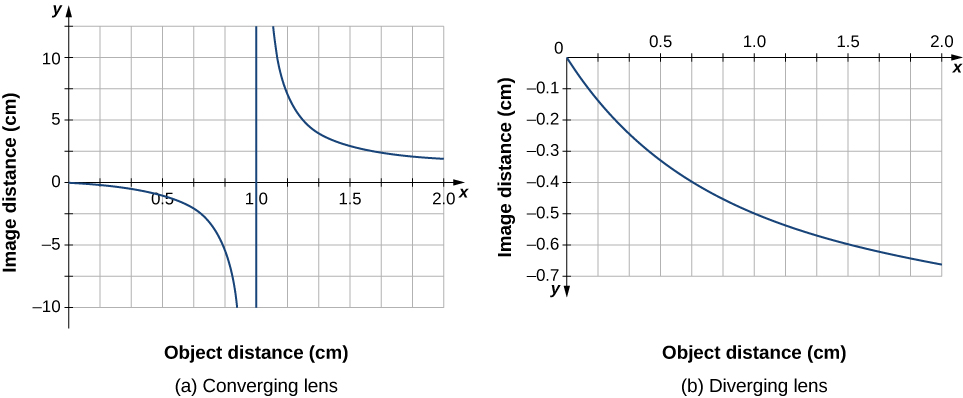
يجب أن ينتج جسم أبعد بكثير من البعد البؤري f من العدسة صورة بالقرب من المستوى البؤري، لأن الحد الثاني على الجانب الأيمن من المعادلة أعلاه يصبح ضئيلًا مقارنة بالحد الأول، لذلك لدينا\(d_i≈f\). يمكن ملاحظة ذلك في مخطط الجزء (أ) من الشكل، الذي يُظهر أن مسافة الصورة تقترب بشكل غير مباشر من الطول البؤري البالغ 1 سم لمسافات الأجسام الأكبر. عندما يقترب الكائن من المستوى البؤري، تتباعد مسافة الصورة إلى اللانهاية الموجبة. هذا أمر متوقع لأن الجسم الموجود على المستوى البؤري ينتج أشعة متوازية تشكل صورة عند اللانهاية (أي بعيدًا جدًا عن العدسة). عندما يكون الكائن أبعد من البعد البؤري للعدسة، تكون مسافة الصورة موجبة، وبالتالي تكون الصورة حقيقية، على الجانب الآخر من العدسة من الكائن، ومعكوسة (بسبب \(m=−d_i/d_o\) المعادلة\ ref {mag}). عندما يكون الكائن أقرب من البعد البؤري للعدسة، تصبح مسافة الصورة سالبة، مما يعني أن الصورة افتراضية، على نفس جانب العدسة مع الكائن، ومستقيمة.

بالنسبة للعدسة المتباينة الرقيقة ذات البعد البؤري\(f =−1.0\, cm\)، يظهر في الشكل رسم مماثل لمسافة الصورة مقابل مسافة الكائن\(\PageIndex{10b}\). في هذه الحالة، تكون مسافة الصورة سالبة لجميع مسافات الكائن الموجبة، مما يعني أن الصورة افتراضية، على نفس جانب العدسة مع الكائن، ومستقيمة. يمكن رؤية هذه الخصائص أيضًا من خلال مخططات تتبع الأشعة (الشكل\(\PageIndex{10}\)).

الشكل\(\PageIndex{10}\): تظهر النقاط الحمراء النقاط البؤرية للعدسات. (أ) صورة حقيقية مقلوبة تتكون من جسم أبعد من البعد البؤري للعدسة المتقاربة. (ب) صورة افتراضية عمودية تتكون من جسم أقرب من البعد البؤري للعدسة. (ج) صورة افتراضية عمودية مكوَّنة من جسم أبعد من البُعد البؤري لعدسة متباينة.

لرؤية مثال ملموس للصور المستقيمة والمقلوبة، انظر إلى الشكل\(\PageIndex{11}\)، الذي يعرض الصور التي تكونت من العدسات المتقاربة عندما يتم وضع الكائن (وجه الشخص في هذه الحالة) على مسافات مختلفة من العدسة. في الجزء (أ) من الشكل، يكون وجه الشخص أبعد من بُعد بؤري واحد عن العدسة، وبالتالي تكون الصورة معكوسة. في الجزء (ب)، يكون وجه الشخص أقرب من بُعد بؤري واحد من العدسة، وبالتالي تكون الصورة في وضع مستقيم.

الشكل\(\PageIndex{11}\): (أ) عندما يتم تثبيت عدسة متقاربة على مسافة أبعد من بُعد بؤري واحد من وجه الرجل، يتم تكوين صورة معكوسة. لاحظ أن الصورة قيد التركيز ولكن الوجه ليس كذلك، لأن الصورة أقرب بكثير إلى الكاميرا التي تلتقط هذه الصورة من الوجه. (ب) يتم إنتاج صورة مستقيمة لوجه الرجل عندما يتم تثبيت عدسة متقاربة بأقل من بُعد بؤري واحد من وجهه. (المرجع: تعديل العمل من قبل «DamongMan» /Flickr؛ الائتمان ب: تعديل العمل من قبل Casey Fleser)

استخدم الأمثلة التالية لفهم كيفية عمل العدسات الرقيقة بشكل أفضل.

إستراتيجية حل المشكلات: العدسات

• الخطوة 1. حدد ما إذا كان تتبع الأشعة أو معادلة العدسة الرقيقة أو كليهما سيكون مفيدًا. حتى إذا لم يتم استخدام تتبع الأشعة، فإن الرسم الدقيق يكون دائمًا مفيدًا جدًا. اكتب الرموز والقيم على الرسم.
• الخطوة 2. حدد ما يجب تحديده في المشكلة (حدد المجهول).
• الخطوة 3. قم بعمل قائمة بما هو معطى أو يمكن استنتاجه من المشكلة (حدد المعروف).
• الخطوة 4. إذا كان تتبع الأشعة مطلوبًا، فاستخدم قواعد تتبع الأشعة المدرجة بالقرب من بداية هذا القسم.
• الخطوة 5. تتطلب معظم المشكلات الكمية استخدام معادلة العدسة الرقيقة و/أو معادلة صانع العدسة. قم بحل هذه المشكلات مع المجهول وأدخل الكميات المعطاة أو استخدم كلاهما معًا للعثور على مجهولين.
• الخطوة 7. تحقق لمعرفة ما إذا كانت الإجابة معقولة. هل العلامات صحيحة؟ هل الرسم التخطيطي أو تتبع الأشعة يتوافق مع الحساب؟

مثال\(\PageIndex{1}\): استخدام معادلة صانع العدسات

أوجد نصف قطر انحناء عدسة ذات مقعر مُؤسَّن بشكل متماثل من زجاج بمعامل انكساره ١٫٥٥؛ بحيث يكون البُعد البؤري للعدسة في الهواء ٢٠ سم (بالنسبة للعدسة ذات المقعر، يكون لكلا السطحين نفس نصف قطر الانحناء).

إستراتيجية

استخدم شكل العدسة الرقيقة لمعادلة صانع العدسات:

\ [\ dfrac {1} {f} =\ يسار (\ dfrac {n_2} {n_1} −1\ يمين)\ يسار (\ dfrac {1} {R_1} −\ dfrac {1} {R_2}\ يمين) \ لا رقم\]

أين\(R_1<0\) و\(R_2>0\). نظرًا لأننا نصنع عدسة ثنائية المقعرة متماثلة، فلدينا\(|R_1|=|R_2|\).

الحل

يمكننا تحديد نصف قطر الانحناء\(R\) من

\ [\ dfrac {1} {f} = \ يسار (\ dfrac {n_2} {n_1} −1\ يمين)\ يسار (\ dfrac {−2} {R}\ يمين). \ لا يوجد رقم\]

حل المشكلة\(R\) وإدخالها\(f=−20\,cm\)\(n_2=1.55\) \(n_1=1.00\) وعطاءها

\ [\ ابدأ {المحاذاة} R &=−2f\ يسار (\ dfrac {n_2} {n_1} −1\ يمين) \ بدون رقم\\\ [4pt] &=−2 (−20\، سم) \ يسار (\ dfrac {1.55} {1.00} −1\ يمين)\ لا رقم\\ [4pt] &= 22\، سم. \ nالرقم\ النهاية {المحاذاة}\ لا يوجد رقم\]

مثال\(\PageIndex{2}\): العدسة المتقاربة ومسافات الأجسام المختلفة

أوجد موقع الصورة واتجاهها وتكبيرها لجسم ارتفاعه ٣٫٠ سم في كل موضع من المواضع التالية أمام عدسة محدبة بُعدها البؤري ١٠٫٠ سم. (أ) \(d_o=50.0\,cm\) و (ب)\(d_o=5.00\,cm\) و (ج)\ (d_o=20.0\، سم\).

إستراتيجية

نبدأ بمعادلة العدسة الرقيقة (المعادلة\ ref { معادلة العدسة الرقيقة})

\[\dfrac{1}{d_i}+\dfrac{1}{d_o}=\dfrac{1}{f}. \nonumber \]

قم بحل هذه المشكلة لمسافة الصورة\(d_i\) وأدخل مسافة الكائن المحددة والبعد البؤري.

الحل

أ- من أجل\(f=+10\, cm\)،\(d_o=50\, cm\) وهذا يعطي

\ [\ ابدأ {المحاذاة} d_i &= \ يسار (\ dfrac {1} {f} −\ dfrac {1} {d_o}\ يمين) ^ {−1}\ لا يوجد رقم\\\ [4pt] &=\ يسار (\ dfrac {1} {10.0\ سم} −\ dfrac {1} -\ dfrac {1} -\ dfrac {1} -\ dfrac {1} -\ dfrac {1} \\ dfraرقم\\ [4pt] &=12.5\، سم\ لا رقم\ نهاية {محاذاة} \ لا رقم\]

الصورة موجبة، وبالتالي فإن الصورة حقيقية، وتقع على الجانب الآخر من العدسة من الجسم، وتبعد 12.6 سم عن العدسة. للعثور على نسبة تكبير الصورة واتجاهها، استخدم

\ [\ ابدأ {المحاذاة} m &=−\ dfrac {d_i} {d_o}\ لا يوجد رقم\\ [4pt] &=−\ dfrac {12.5\، سم} {50.0\، سم}\ لا رقم\\ [4pt] &=−0.250. \ nالرقم\ النهاية {المحاذاة}\ لا يوجد رقم\]

التكبير السلبي يعني أن الصورة معكوسة. نظرًا لأن\(|m|<1\) الصورة أصغر من الكائن. يتم تحديد حجم الصورة من خلال

\ [\ ابدأ {المحاذاة} |h_i| &=|m|h_o \ بدون رقم\\ [4pt] & =( 0.250) (3.0\، سم)\ بدون رقم\\ [4pt] &=0.75\، سم\ لا رقم\ نهاية {محاذاة}\ لا رقم\]

(ب) من أجل\(d_o=5.00\,cm\) و\(f=+10.0\,cm\)

\ [\ ابدأ {المحاذاة} d_i&=\ لليسار (\ dfrac {1} {f} −\ dfrac {1} {d_o}\ اليمين) ^ {−1}\ بدون رقم\\\ [4pt] &=\ يسار ( \ dfrac {1} {10.0\ سم} −\ dfrac {1} -\ dfrac {1} -\ dfrac {1} -\ dfrac {1} -\ dfrac {1} -\ dfrac\ لا يوجد رقم\\ [4pt] &=−10.0\، سم \ لا رقم\ نهاية {محاذاة}\ لا رقم\]

مسافة الصورة سالبة، وبالتالي تكون الصورة افتراضية، وتقع على نفس جانب العدسة مع الكائن، وتبعد 10 سم عن العدسة. تم العثور على تكبير الصورة واتجاهها من

\ [\ ابدأ {المحاذاة} m &=−\ dfrac {d_i} {d_o}\ لا يوجد رقم\\ [4pt] &=−\ dfrac {−10.0\، سم} {5.00\، سم}\ لا رقم\\ [4pt] &=+2.00. \ nالرقم\ النهاية {المحاذاة}\ لا يوجد رقم\]

التكبير الإيجابي يعني أن الصورة مستقيمة (أي أنها لها نفس اتجاه الكائن). نظرًا لأن \(|m|>0\) الصورة أكبر من الكائن. حجم الصورة

\ [\ ابدأ {المحاذاة} |h_i|&=|m|h_o\ بدون رقم\\ [4pt] & =( 2.00) (3.0\، سم)\ بدون رقم\\ [4pt] &=6.0\، سم. \ nالرقم \ النهاية {المحاذاة}\ لا يوجد رقم\]

(ج) من أجل\(d_o=20\,cm\) و\(f=+10cm\)

\ [\ ابدأ {المحاذاة} d_i &= \ يسار (\ dfrac {1} {f} −\ dfrac {1} {d_o}\ يمين) ^ {−1}\ لا يوجد رقم\\\ [4pt] &=\ يسار (\ dfrac {1} {10.0\ سم} −\ dfrac {1} -\ dfrac {1} -\ dfrac {1} -\ dfrac {1} −\ dfrac {1} \ dfrac}\ لا يوجد رقم\\ [4pt] &=20.0\، سم\ لا رقم\ نهاية {محاذاة} \ لا رقم\]

مسافة الصورة موجبة، وبالتالي فإن الصورة حقيقية، وتقع على الجانب الآخر للعدسة من الجسم، وتبعد 20.0 سم عن العدسة. التكبير هو

\ [\ ابدأ {المحاذاة} m &=−\ dfrac {d_i} {d_o}\ لا يوجد رقم\\ [4pt] &=−\ dfrac {20.0\، سم} {20.0\، سم}\ لا رقم\\ [4pt] &=−1.00. \ nالرقم\ النهاية {المحاذاة}\ لا يوجد رقم\]

التكبير السلبي يعني أن الصورة معكوسة. نظرًا لأن\(|m|=1\) الصورة بنفس حجم الكائن.

عند حل المشكلات في البصريات الهندسية، نحتاج غالبًا إلى الجمع بين تتبع الأشعة ومعادلات العدسة. يوضح المثال التالي هذا النهج.

مثال\(\PageIndex{3}\): اختيار الطول البؤري ونوع العدسة

لعرض صورة لمصباح كهربائي على شاشة تبعد 1.50 مترًا، تحتاج إلى اختيار نوع العدسة التي تريد استخدامها (متقاربة أو متباينة) وطولها البؤري (الشكل\(\PageIndex{12}\)). تم تحديد المسافة بين العدسة والمصباح عند 0.75 مترًا، وما مدى تكبير الصورة واتجاهها؟

الشكل\(\PageIndex{12}\): مصباح كهربائي يقع على بعد 0.75 مترًا من عدسة ذات طول بؤري يبلغ 0.50 مترًا ينتج صورة حقيقية على الشاشة، كما تمت مناقشته في المثال. يتنبأ تتبع الأشعة بموقع الصورة وحجمها.

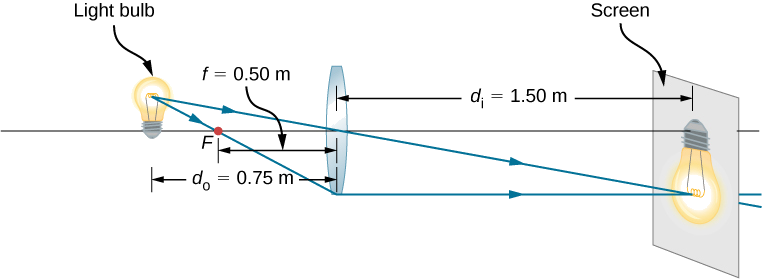
إستراتيجية

يجب أن تكون الصورة حقيقية، لذلك تختار استخدام عدسة متقاربة. يمكن العثور على البعد البؤري باستخدام معادلة العدسة الرقيقة وحل البعد البؤري. مسافة الكائن هي \(d_o=0.75\,m\) ومسافة الصورة هي\(d_i=1.5\,m\).

الحل

قم بحل العدسة الرقيقة للبعد البؤري وأدخل مسافات الكائن والصورة المطلوبة:

\ [\ ابدأ {المحاذاة} \ dfrac {1} {d_o} +\ dfrac {1} {d_i} &=\ dfrac {1} {f}\ بدون رقم\\\ [4pt] f &=\ يسار (\ dfrac {1} {d_o} +\ dfrac {1} {d_i}\ يمين) ^ {−1}\ لا يوجد رقم \\ [4pt] &= \ يسار (\ dfrac {1} {0.75\، م} +\ dfrac {1} {1.5\، م}\ يمين) ^ {−1}\ لا يوجد رقم \\[4pt] &= 0.50 \, m \nonumber \end{align} \nonumber \]

التكبير هو

\ [\ ابدأ {المحاذاة} m &=−\ dfrac {d_i} {d_o}\ لا يوجد رقم\\ [4pt] &= −\ dfrac {1.5\، م} {0.75\، م}\ لا رقم\\ [4pt] &=−2.0. \ nالرقم \ النهاية {المحاذاة}\ لا يوجد رقم\]

الدلالة

تعني علامة الطرح الخاصة بالتكبير أن الصورة معكوسة. البعد البؤري إيجابي، كما هو متوقع للعدسة المتقاربة. يمكن استخدام تتبع الأشعة للتحقق من الحساب (الشكل\(\PageIndex{12}\)). كما هو متوقع، تكون الصورة معكوسة وحقيقية وأكبر من الكائن.