2.6: العين
- Page ID
- 196787
في نهاية هذا القسم، ستكون قادرًا على:
- فهم الفيزياء الأساسية لكيفية تكوين الصور بالعين البشرية
- تعرف على العديد من حالات ضعف الرؤية بالإضافة إلى المبادئ البصرية لعلاج هذه الحالات
فيزياء العين
تعتبر العين رائعة في كيفية تشكيل الصور وفي ثراء التفاصيل والألوان التي يمكن اكتشافها. ومع ذلك، غالبًا ما تحتاج أعيننا إلى بعض التصحيح للوصول إلى ما يسمى بالرؤية «الطبيعية». في الواقع، يجب تسمية الرؤية الطبيعية بالرؤية «المثالية» لأن ما يقرب من نصف السكان يحتاجون إلى نوع من تصحيح البصر، لذا فإن الحاجة إلى النظارات ليست بأي حال من الأحوال «غير طبيعية». يمكن تحليل تكوين الصورة بأعيننا وتصحيح الرؤية المشترك باستخدام البصريات التي تمت مناقشتها سابقًا في هذا الفصل.
\(\PageIndex{1}\)يوضح الشكل التشريح الأساسي للعين. تشكل القرنية والعدسة نظامًا يعمل، بشكل تقريبي جيد، كعدسة رقيقة واحدة. للحصول على رؤية واضحة، يجب عرض صورة حقيقية على شبكية العين الحساسة للضوء، والتي تقع على مسافة ثابتة من العدسة. تسمح العدسة المرنة للعين بتعديل نصف قطر انحناء العدسة لإنتاج صورة على شبكية العين للأشياء على مسافات مختلفة. يقع مركز الصورة على النقرة، التي تحتوي على أكبر كثافة لمستقبلات الضوء وأكبر حدة (حدة) في المجال البصري. تسمح الفتحة المتغيرة (أي حدقة العين)، جنبًا إلى جنب مع التكيف الكيميائي، للعين باكتشاف شدة الضوء من أدنى مستوى يمكن ملاحظته إلى 10 10 مرات أكبر (بدون ضرر). هذا نطاق مذهل من الاكتشاف. تبدأ معالجة النبضات العصبية البصرية بالترابط في شبكية العين وتستمر في الدماغ. ينقل العصب البصري الإشارات التي تستقبلها العين إلى الدماغ.
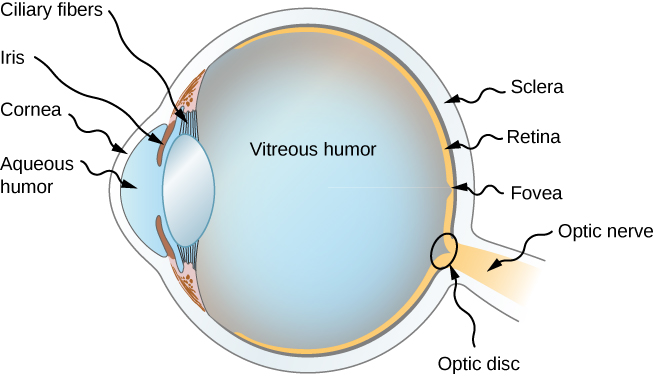
تعتبر مؤشرات الانكسار في العين ضرورية لقدرتها على تكوين الصور. \(\PageIndex{1}\)يسرد الجدول مؤشرات الانكسار ذات الصلة بالعين. يحدث أكبر تغيير في معامل الانكسار، وهو المكان الذي تكون فيه أشعة الضوء أكثر انحناءًا، في الواجهة الهوائية للقرنية بدلاً من واجهة العدسة الفكاهية المائية. يوضح مخطط الأشعة في الشكل\(\PageIndex{2}\) تكوين الصورة بواسطة القرنية وعدسة العين. توفر القرنية، وهي بحد ذاتها عدسة متقاربة بطول بؤري يبلغ حوالي 2.3 سم، معظم قوة التركيز للعين. توفر العدسة، وهي عدسة متقاربة بطول بؤري يبلغ حوالي 6.4 سم، التركيز الدقيق المطلوب لإنتاج صورة واضحة على شبكية العين. يمكن معالجة القرنية والعدسة كعدسة رقيقة واحدة، على الرغم من مرور أشعة الضوء عبر عدة طبقات من المواد (مثل القرنية، والفكاهة المائية، وعدة طبقات في العدسة، والفكاهة الزجاجية)، وتغيير الاتجاه في كل واجهة. الصورة المتكونة تشبه إلى حد كبير الصورة التي تنتجها عدسة محدبة واحدة (أي صورة حقيقية مقلوبة). على الرغم من أن الصور المتكونة في العين مقلوبة، فإن الدماغ يقلبها مرة أخرى لجعلها تبدو مستقيمة.
| مادة | مؤشر الانكسار |
|---|---|
| الماء | 1.33 |
| الهواء | 1.0 |
| قرنية | 1.38 |
| فكاهة مائية | 1.34 |
| عدسة | 1.41 * |
| الفكاهة الزجاجية | 1.34 |
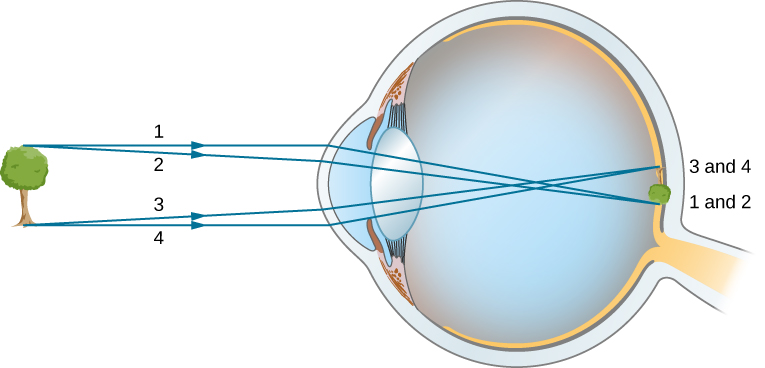
كما لوحظ، يجب أن تسقط الصورة بدقة على شبكية العين لإنتاج رؤية واضحة - أي أن مسافة الصورة d i يجب أن تساوي المسافة بين العدسة والشبكية. نظرًا لأن المسافة بين العدسة والشبكية لا تتغير، يجب أن تكون مسافة الصورة d i هي نفسها للكائنات على جميع المسافات. تقوم العضلات الهدبية بضبط شكل عدسة العين للتركيز على الأشياء القريبة أو البعيدة. من خلال تغيير شكل عدسة العين، تقوم العين بتغيير البعد البؤري للعدسة. تسمى آلية العين هذه بالإقامة.
تُسمى أقرب نقطة يمكن وضع جسم فيها بحيث تتمكن العين من تكوين صورة واضحة على شبكية العين بالنقطة القريبة للعين. وبالمثل، فإن النقطة البعيدة هي أبعد مسافة يمكن من خلالها رؤية الكائن بوضوح. يمكن لأي شخص يتمتع برؤية طبيعية رؤية الأشياء بوضوح على مسافات تتراوح من 25 سم إلى ما لا نهاية بشكل أساسي. تزداد النقطة القريبة مع تقدم العمر، لتصبح عدة أمتار لبعض كبار السن. في هذا النص، نعتبر أن النقطة القريبة هي 25 سم.
يمكننا استخدام معادلات العدسة الرقيقة لفحص تكوين الصورة عن طريق العين كميًا. أولاً، نحدد القوة الضوئية للعدسة على النحو التالي
\[P=\frac{1}{f} \nonumber \]
مع البعد البؤري المحدد بالأمتار. تسمى وحدات الطاقة الضوئية «الديوبتر» (D). أي 1D = 1/م، أو 1 م −1. يصف أخصائيو البصريات النظارات الشائعة والعدسات اللاصقة في وحدات الديوبتر. باستخدام هذا التعريف للقوة الضوئية، يمكننا إعادة كتابة معادلات العدسة الرقيقة على النحو التالي
\[P=\frac{1}{d_o}+\frac{1}{d_i}. \nonumber \]
يعد العمل باستخدام الطاقة الضوئية أمرًا مريحًا لأنه بالنسبة لعدستين أو أكثر قريبتين من بعضهما البعض، تكون الطاقة الضوئية الفعالة لنظام العدسة تقريبًا مجموع الطاقة الضوئية للعدسات الفردية:
\[P_{total}=P_{lens~1}+P_{lens~2}+P_{lens~3}+⋯ \label{sumlens} \]
يبلغ طول بؤري القرنية وعدسة العين 2.3 و6.4 سم على التوالي. ابحث عن الطول البؤري الصافي والقوة البصرية للعين.
إستراتيجية
وتضيف القوى البصرية للعدسات المتقاربة، إلى ذلك\(P_{eye}=P_{cornea}+P_{lens}\).
الحل
تعطي كتابة معادلة القوة بدلالة الأطوال البؤرية
\[\frac{1}{f_{eye}}=\frac{1}{f_{cornea}}+\frac{1}{f_{lens}}=\frac{1}{2.3cm}+\frac{1}{6.4cm} \nonumber. \nonumber \]
وبالتالي، فإن البعد البؤري للعين (القرنية والعدسة معًا) هو
\[f_{eye}=1.69cm. \nonumber \]
القوة البصرية للعين هي
\[P_{eye}=\frac{1}{f_{eye}}=\frac{1}{0.0169m}=59D. \nonumber \]
للحصول على رؤية واضحة،\(d_i\) يجب أن تساوي مسافة الصورة المسافة بين العدسة والشبكية. الرؤية العادية ممكنة للأشياء على مسافات تصل\(d_o=25\, cm\) إلى ما لا نهاية. يوضح المثال التالي كيفية حساب مسافة الصورة لكائن تم وضعه في النقطة القريبة من العين.
يبلغ الطول البؤري الصافي لعين بشرية معينة 1.7 سم. يتم وضع جسم في النقطة القريبة من العين. إلى أي مدى يتم تشكيل صورة مركزة خلف العدسة؟
إستراتيجية
تقع النقطة القريبة على بعد 25 سم من العين، وبالتالي فإن مسافة الكائن هي d o = 25 سم. نحدد مسافة الصورة من معادلة العدسة:
\[\frac{1}{d_i}=\frac{1}{f}−\frac{1}{d_o}. \nonumber \]
الحل
\[d_i=(\frac{1}{f}−\frac{1}{d_o})^{−1} \nonumber \]
\[=(\frac{1}{1.7cm}−\frac{1}{25cm})^{−1} \nonumber \]
\[=1.8cm \nonumber \]
لذلك، يتم تشكيل الصورة خلف العدسة بمقدار 1.8 سم.
الدلالة
من صيغة التكبير، نجد\(m=−\frac{1.8cm}{25cm}=−0.073\). نظرًا لأن m<0، يتم عكس الصورة في الاتجاه فيما يتعلق بالكائن. من القيمة المطلقة لـ m نرى أن الصورة أصغر بكثير من الكائن؛ في الواقع، إنها 7٪ فقط من حجم الكائن.
تصحيح الرؤية
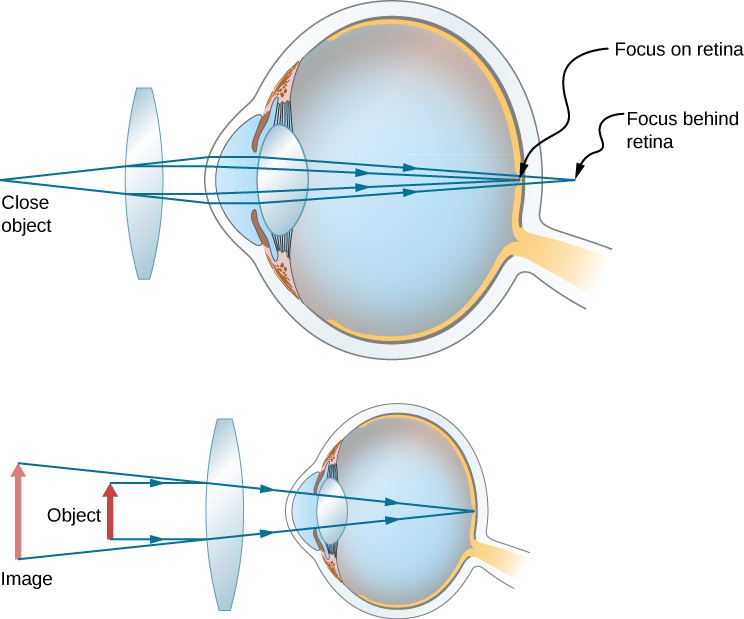
إن الحاجة إلى نوع من تصحيح الرؤية شائعة جدًا. من السهل فهم عيوب الرؤية النموذجية باستخدام البصريات الهندسية، وبعضها سهل التصحيح. \(\PageIndex{3}\)يوضح الشكل اثنين من عيوب الرؤية الشائعة. قصر النظر، أو قصر النظر، هو القدرة على رؤية الأشياء القريبة، في حين أن الأشياء البعيدة ضبابية. تتقارب العين فوق الأشعة المتوازية تقريبًا من جسم بعيد، وتتقاطع الأشعة أمام شبكية العين. يتم تقريب المزيد من الأشعة المتباينة من جسم قريب على شبكية العين للحصول على صورة واضحة. تُسمى المسافة إلى أبعد جسم يمكن رؤيته بوضوح بالنقطة البعيدة للعين (عادةً ما تكون النقطة البعيدة عند اللانهاية). طول النظر، أو مد البصر، هو القدرة على رؤية الأشياء البعيدة بوضوح، في حين أن الأشياء القريبة ضبابية. لا تقوم العين البعيدة النظر بتقريب الأشعة من جسم قريب بشكل كافٍ لجعل الأشعة تلتقي على شبكية العين.
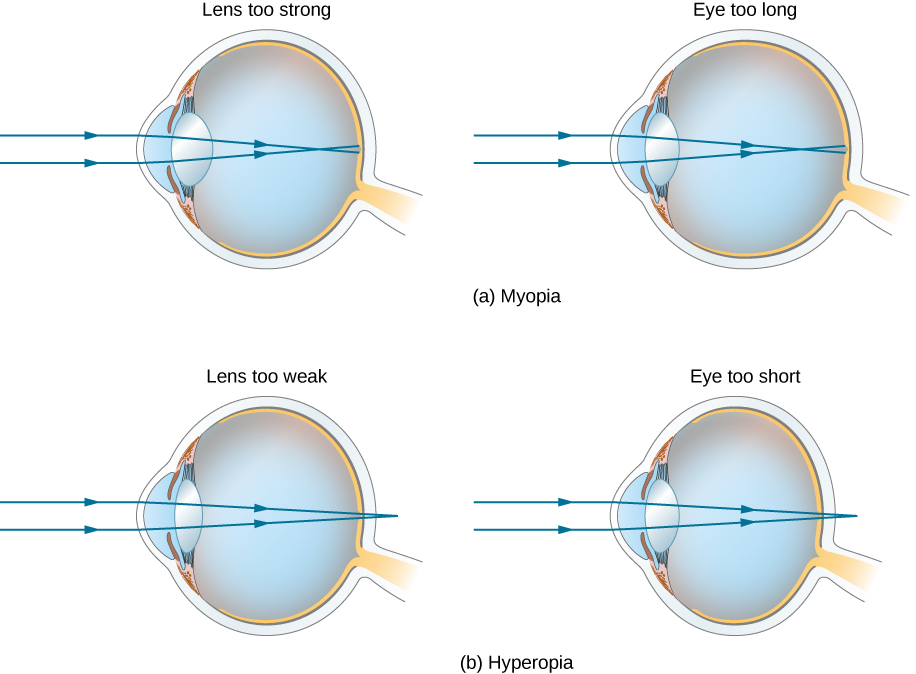
نظرًا لأن العين ذات قصر النظر فوق أشعة الضوء المتقاربة، فإن تصحيح قصر النظر يتمثل في وضع عدسة نظارة متباينة أمام العين، كما هو موضح في الشكل\(\PageIndex{4}\). هذا يقلل من القوة البصرية للعين القوية جدًا (تذكر أن البعد البؤري للعدسة المتباينة سلبي، وبالتالي فإن قوتها البصرية سلبية). هناك طريقة أخرى لفهم هذا التصحيح وهي أن العدسة المتباينة ستؤدي إلى تباعد الأشعة الواردة أكثر للتعويض عن التقارب المفرط الناجم عن نظام عدسة العين. تعمل الصورة التي تنتجها عدسة النظارات المتباينة كجسم (بصري) للعين، ولأن العين لا تستطيع التركيز على الأشياء خارج النقطة البعيدة، يجب أن تشكل العدسة المتباينة صورة لأجسام بعيدة (مادية) عند نقطة أقرب من النقطة البعيدة.
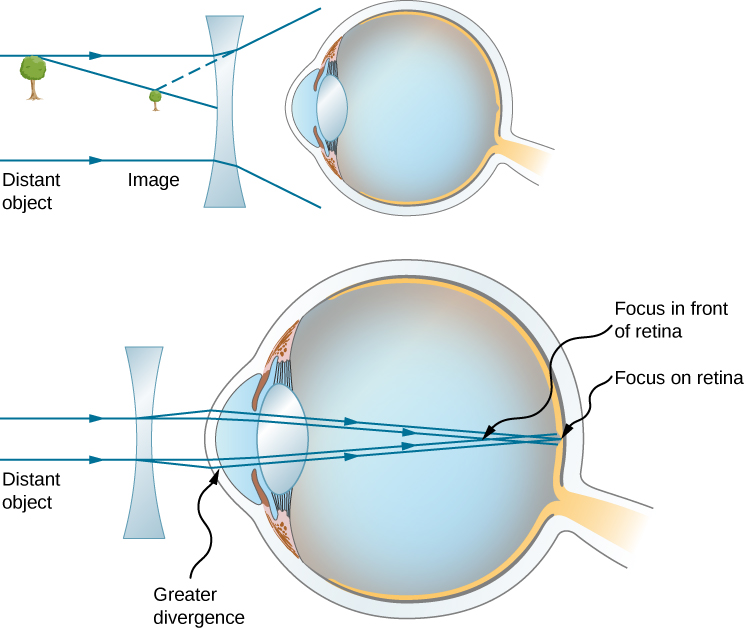
ما القوة البصرية لعدسة النظارات اللازمة لتصحيح رؤية شخص قصير النظر نقطته البعيدة 30.0 سم؟ افترض أن العدسة التصحيحية مثبتة على بعد 1.50 سم من العين.
إستراتيجية
تريد أن يكون هذا الشخص قصير النظر قادرًا على رؤية الأشياء البعيدة بوضوح، مما يعني أن عدسة النظارات يجب أن تنتج صورة على بعد 30.0 سم من العين لشيء في اللانهاية. ستكون الصورة على بُعد 30.0 سم من العين على بُعد 30.0 سم−1.50 سم=28.5 سم من عدسة النظارات. لذلك، يجب أن يكون لدينا d i =−28.5 سم عندما d o =\(\infty\). مسافة الصورة سالبة لأنها تقع على نفس جانب عدسة النظارات مع الكائن.
الحل
نظرًا لأن di و dodo معروفان، يمكننا العثور على القوة البصرية لعدسة النظارات باستخدام Equation\ ref {sumdiv}:
\[P=\frac{1}{d_o}+\frac{1}{d_i}=\frac{1}{\infty}+\frac{1}{−0.285m}=−3.51D. \nonumber \]
الدلالة
تشير القدرة الضوئية السالبة إلى عدسة متباينة (أو مقعرة)، كما هو متوقع. إذا قمت بفحص النظارات للأشخاص الذين يعانون من قصر النظر، ستجد العدسات الأقل سمكًا في المركز. بالإضافة إلى ذلك، إذا قمت بفحص وصفة طبية للنظارات للأشخاص الذين يعانون من قصر النظر، ستجد أن الطاقة البصرية الموصوفة سلبية ويتم إعطاؤها في وحدات الديوبتر.
يتكون تصحيح طول النظر ببساطة من استخدام النوع المعاكس من العدسات المستخدمة في قصر النظر (أي العدسة المتقاربة)، كما هو موضح في الشكل\(\PageIndex{5}\).
ستنتج هذه العدسة صورة لأجسام مادية أقرب من النقطة القريبة على مسافة بين النقطة القريبة والنقطة البعيدة، بحيث يمكن للشخص رؤية الصورة بوضوح. لتحديد الطاقة الضوئية اللازمة للتصحيح، يجب عليك معرفة النقطة القريبة للشخص، كما هو موضح في المثال\(\PageIndex{4}\).
ما القدرة البصرية لعدسة النظارات اللازمة للسماح لشخص بعيد النظر، نقطته القريبة 1.00 متر، برؤية جسم بوضوح على بُعد 25.0 سم من العين؟ افترض أن العدسة التصحيحية مثبتة على بعد 1.5 سم من العين.
إستراتيجية
عندما يكون الجسم على بعد 25.0 سم من عيني الشخص، يجب أن تنتج عدسة النظارات صورة على بعد 1.00 متر (النقطة القريبة)، حتى يتمكن الشخص من رؤيتها بوضوح. ستكون الصورة على بعد 1.00 متر من العين على بعد 100 سم−1.5 سم = 98.5 سم من عدسة النظارات لأن عدسة النظارات تبعد 1.5 سم عن العين. لذلك، d i =−98.5 سم، حيث تشير علامة الطرح إلى أن الصورة موجودة على نفس جانب العدسة مع الكائن. يقع الجسم على بعد 25.0 سم −1.5 سم = 23.5 سم من عدسة النظارات، لذلك d o = 23.5 سم.
الحل
نظرًا لأن di و dodo معروفان، يمكننا العثور على القوة البصرية لعدسة النظارات باستخدام Equation\ ref {sumlens}:
\[P=\frac{1}{d_o}+\frac{1}{d_i}=\frac{1}{0.285m}+\frac{1}{-0.985m}=+3.24D. \nonumber \]
الدلالة
تشير القدرة الضوئية الإيجابية إلى عدسة متقاربة (محدبة)، كما هو متوقع. إذا قمت بفحص نظارات الأشخاص الذين يعانون من بُعد النظر، ستجد العدسات الأكثر سمكًا في المركز. بالإضافة إلى ذلك، تتمتع النظارات الطبية للأشخاص ذوي الرؤية البعيدة بقوة بصرية موصوفة وهي إيجابية.


