2.3: مرايا كروية
- Page ID
- 196755
في نهاية هذا القسم، ستكون قادرًا على:
- وصف تكوين الصورة بواسطة المرايا الكروية.
- استخدم مخططات الأشعة ومعادلة المرآة لحساب خصائص صورة في مرآة كروية.
الصورة في المرآة المستوية لها نفس حجم الكائن، وهي في وضع مستقيم، وهي نفس المسافة خلف المرآة حيث يكون الكائن أمام المرآة. من ناحية أخرى، يمكن للمرآة المنحنية أن تشكل صورًا قد تكون أكبر أو أصغر من الكائن وقد تتشكل إما أمام المرآة أو خلفها. بشكل عام، سيشكل أي سطح منحني صورة، على الرغم من أن بعض الصور تكون مشوهة جدًا بحيث لا يمكن التعرف عليها (فكر في المرايا المنزلية الممتعة). نظرًا لأن المرايا المنحنية يمكنها إنشاء مجموعة متنوعة غنية من الصور، يتم استخدامها في العديد من الأجهزة البصرية التي تجد العديد من الاستخدامات. سنركز على المرايا الكروية في الغالب، لأنها أسهل في التصنيع من المرايا مثل المرايا المكافئة وبالتالي فهي أكثر شيوعًا.
مرايا منحنية
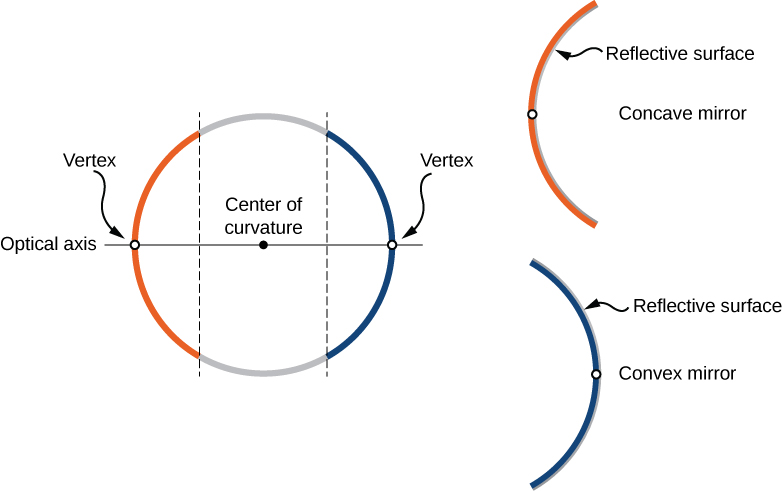
يمكننا تحديد نوعين عامين من المرايا الكروية. إذا كان السطح العاكس هو الجانب الخارجي للكرة، فإن المرآة تسمى مرآة محدبة. إذا كان السطح الداخلي هو السطح العاكس، فإنه يطلق عليه مرآة مقعرة.
التماثل هو أحد السمات المميزة للعديد من الأجهزة البصرية، بما في ذلك المرايا والعدسات. غالبًا ما يُطلق على محور التماثل لهذه العناصر البصرية المحور الرئيسي أو المحور البصري. بالنسبة للمرآة الكروية، يمر المحور البصري عبر مركز انحناء المرآة ورأس المرآة، كما هو موضح في الشكل\(\PageIndex{1}\).
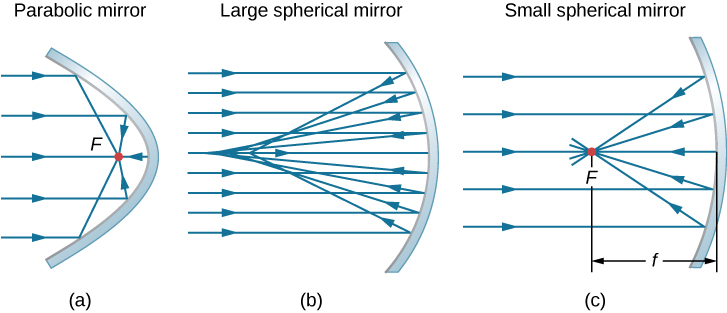
ضع في اعتبارك الأشعة الموازية للمحور البصري لمرآة القطع المكافئ، كما هو موضح في الشكل\(\PageIndex{2a}\). وفقًا لقانون الانعكاس، تنعكس هذه الأشعة بحيث تتقارب عند نقطة تسمى النقطة المحورية. \(\PageIndex{2b}\)يوضِّح الشكل مرآة كروية كبيرة الحجم مقارنة بنصف قطر انحنائها. بالنسبة لهذه المرآة، لا تتقاطع الأشعة المنعكسة عند نفس النقطة، لذلك لا تحتوي المرآة على نقطة محورية محددة جيدًا. وهذا ما يسمى بالانحراف الكروي وينتج عنه صورة غير واضحة لكائن ممتد. \(\PageIndex{2c}\)يوضِّح الشكل مرآة كروية صغيرة مقارنة بنصف قطر انحنائها. هذه المرآة عبارة عن تقريب جيد لمرآة القطع المكافئ، لذلك تنعكس الأشعة التي تصل بالتوازي مع المحور البصري إلى نقطة محورية محددة جيدًا. تسمى المسافة على طول المحور البصري من المرآة إلى النقطة البؤرية بالبعد البؤري للمرآة.
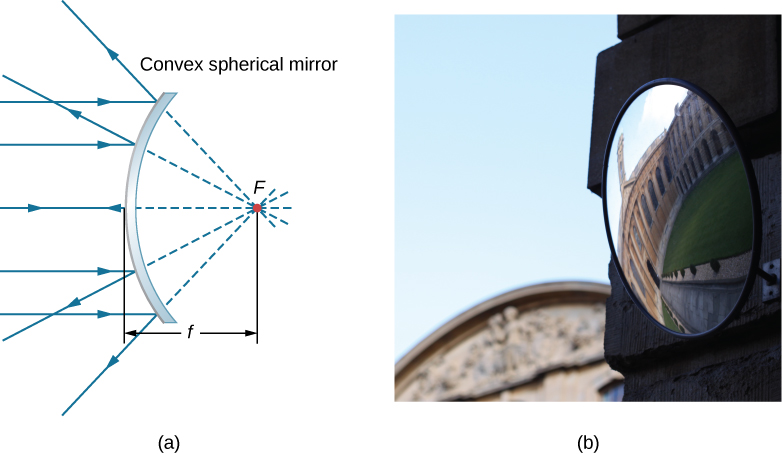
تحتوي المرآة الكروية المحدبة أيضًا على نقطة محورية، كما هو موضح في الشكل\(\PageIndex{3}\). تنعكس الأشعة الساقطة الموازية للمحور البصري من المرآة ويبدو أنها تنشأ من نقطة\(F\) على بعد بؤري\(f\) خلف المرآة. وبالتالي، فإن النقطة البؤرية افتراضية لأنه لا توجد أشعة حقيقية تمر عبرها فعليًا؛ يبدو أنها تنبع منها فقط.
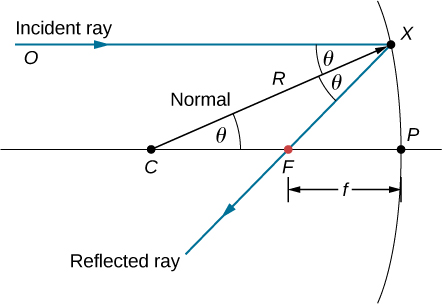
كيف يرتبط البعد البؤري للمرآة بنصف قطر انحناء المرآة؟ \(\PageIndex{4}\)يوضِّح الشكل شعاعًا واحدًا ينعكس بواسطة مرآة كروية مقعرة. الشعاع الساقط موازٍ للمحور البصري. النقطة التي يعبر عندها الشعاع المنعكس المحور البصري هي النقطة البؤرية. لاحظ أن جميع الأشعة الساقطة الموازية للمحور البصري تنعكس من خلال النقطة البؤرية - نعرض شعاعًا واحدًا فقط من أجل البساطة. نريد أن نجد كيف يرتبط الطول البؤري\(FP\) (المشار إليه بـ\(f\)) بنصف قطر انحناء المرآة\(R\)، التي يبلغ طولها
\[R=CF+FP. \label{eq31} \]
يخبرنا قانون الانعكاس أن الزوايا\(\angle OXC\)\(\angle CXF\) هي نفسها، ولأن الشعاع الساقط موازٍ للمحور البصري\(\angle OXC\)\(\angle XCP\) والزوايا وهو نفسه أيضًا. وبالتالي، فإن المثلث\(CXF\) هو مثلث متساوي الساقين مع\(CF=FX\). إذا كانت\(θ\) الزاوية صغيرة،
\[\sin θ≈ θ \label{sma} \]
وهو ما يسمى «تقريب الزاوية الصغيرة»)، ثم\(FX≈FP\) أو\(CF≈FP\). إدراج هذا في المعادلة\ ref {eq31} لنصف القطر\(R\)، نحصل عليه
\[\begin{align} R &=CF+FP \nonumber \\[4pt] &=FP+FP \nonumber \\[4pt] &=2FP\nonumber \\[4pt] &=2f \end{align} \nonumber \]
بعبارة أخرى، في التقريب ذي الزاوية الصغيرة، يكون الطول\(f\) البؤري للمرآة الكروية المقعرة نصف نصف قطر انحنائها،\(R\):
\[f=\dfrac{R}{2}. \nonumber \]
في هذا الفصل، نفترض أن تقريب الزاوية الصغيرة (المعروف أيضًا بالتقريب المحوري) يكون دائمًا صالحًا. في هذا التقريب، تكون جميع الأشعة عبارة عن أشعة شبه محورية، مما يعني أنها تصنع زاوية صغيرة مع المحور البصري وتكون على مسافة أقل بكثير من نصف قطر الانحناء من المحور البصري. في هذه الحالة، تكون\(θ\) زوايا انعكاسها زوايا صغيرة، لذلك
\[\sin θ≈ \tan θ≈ θ. \label{smallangle} \]
استخدام تتبع الأشعة لتحديد موقع الصور
للعثور على موقع صورة مكونة من مرآة كروية، نستخدم أولاً تتبع الأشعة، وهو أسلوب رسم الأشعة واستخدام قانون الانعكاس لتحديد الأشعة المنعكسة (فيما بعد، بالنسبة للعدسات، نستخدم قانون الانكسار لتحديد الأشعة المنكسرة). بالاقتران مع بعض الهندسة الأساسية، يمكننا استخدام تتبع الأشعة للعثور على النقطة البؤرية وموقع الصورة ومعلومات أخرى حول كيفية معالجة المرآة للضوء. في الواقع، استخدمنا بالفعل تتبع الأشعة أعلاه لتحديد النقطة البؤرية للمرايا الكروية، أو مسافة الصورة للمرايا المسطحة. لتحديد موقع صورة كائن، يجب تحديد نقطتين على الأقل من الصورة. يتطلب تحديد موقع كل نقطة رسم شعاعين على الأقل من نقطة على الكائن وإنشاء أشعة منعكسة. النقطة التي تتقاطع عندها الأشعة المنعكسة، إما في الفضاء الحقيقي أو في الفضاء الافتراضي، هي المكان الذي توجد فيه النقطة المقابلة للصورة. لتسهيل تتبع الأشعة، نركز على أربعة أشعة «رئيسية» يسهل تكوين انعكاساتها.
\(\PageIndex{5}\)يُظهر الشكل مرآة مقعرة ومرآة محدبة، ولكل منها جسم على شكل سهم. هذه هي الكائنات التي نريد تحديد صورها عن طريق تتبع الأشعة. للقيام بذلك، نرسم الأشعة من النقطة\(Q\) الموجودة على الكائن ولكن ليس على المحور البصري. نختار رسم شعاعنا من طرف الكائن. ينتقل الشعاع الرئيسي 1 من النقطة\(Q\) وينتقل بالتوازي مع المحور البصري. يجب أن يمر انعكاس هذا الشعاع عبر النقطة المحورية، كما هو موضح أعلاه. وهكذا، بالنسبة للمرآة المقعرة، يمر انعكاس الشعاع الرئيسي 1 عبر النقطة البؤرية\(F\)، كما هو موضح في الشكل\(\PageIndex{5b}\). بالنسبة للمرآة المحدبة، يمر الامتداد الخلفي لانعكاس الشعاع الرئيسي 1 عبر النقطة البؤرية (أي التركيز الافتراضي). ينتقل الشعاع الرئيسي 2 أولاً على الخط الذي يمر عبر النقطة البؤرية ثم ينعكس مرة أخرى على طول خط موازٍ للمحور البصري. ينتقل الشعاع الرئيسي 3 نحو مركز انحناء المرآة، لذلك يصطدم بالمرآة عند السقوط الطبيعي وينعكس مرة أخرى على طول الخط الذي جاء منه. وأخيرًا، يصطدم الشعاع الرئيسي 4 برأس المرآة وينعكس بشكل متماثل حول المحور البصري.
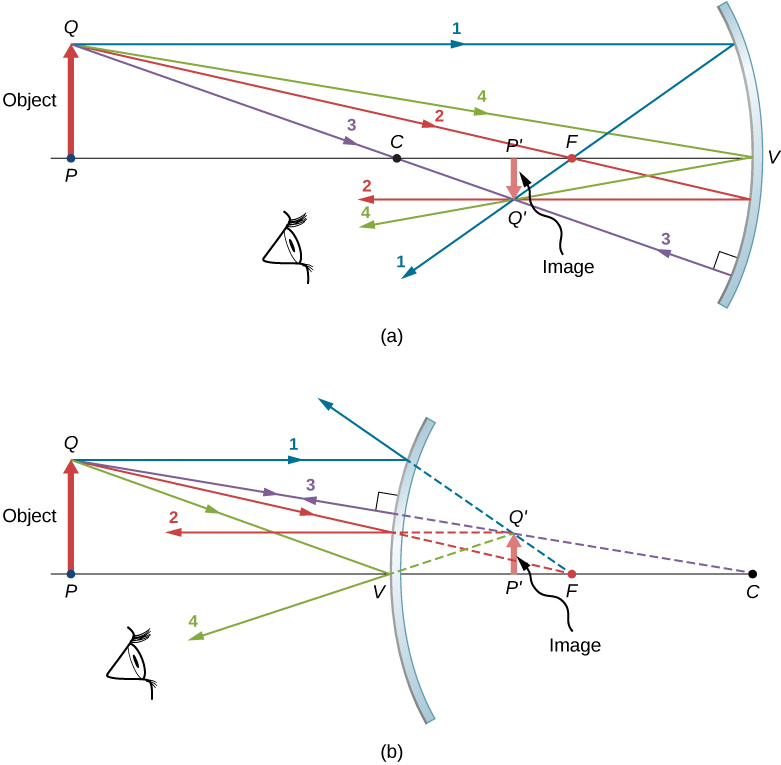
تتقاطع الأشعة الأربعة الرئيسية عند النقطة\(Q′\)، وهي المكان الذي\(Q\) توجد فيه صورة النقطة. لتحديد النقطة\(Q′\)، يكفي رسم أي شعاعين من هذه الأشعة الأساسية. وبالتالي فنحن أحرار في اختيار أي من الأشعة الرئيسية التي نرغب في تحديد موقع الصورة. أحيانًا يكون رسم أكثر من شعاعين رئيسيين مفيدًا للتحقق من صحة تتبع الأشعة.
لتحديد موقع الصورة الموسعة بالكامل، نحتاج إلى تحديد نقطة ثانية في الصورة، حتى نعرف كيفية توجيه الصورة. للقيام بذلك، نتتبع الأشعة الرئيسية من قاعدة الكائن. في هذه الحالة، تمتد جميع الأشعة الرئيسية الأربعة على طول المحور البصري، وتنعكس من المرآة، ثم تعود إلى المحور البصري. تكمن الصعوبة في أنه نظرًا لأن هذه الأشعة متوازية، لا يمكننا تحديد نقطة فريدة تتقاطع فيها. كل ما نعرفه هو أن قاعدة الصورة موجودة على المحور البصري. ومع ذلك، نظرًا لأن المرآة متماثلة من الأعلى إلى الأسفل، فإنها لا تغير الاتجاه الرأسي للكائن. وبالتالي، نظرًا لأن الكائن عمودي، يجب أن تكون الصورة عمودية. لذلك، تكون صورة قاعدة الكائن على المحور البصري مباشرة فوق صورة الطرف، كما هو موضح في الشكل.
بالنسبة للمرآة المقعرة، تتشكل الصورة الموسعة في هذه الحالة بين النقطة البؤرية ومركز انحناء المرآة. يتم عكسها فيما يتعلق بالكائن، وهي صورة حقيقية، وهي أصغر من الكائن. إذا قمنا بتحريك الكائن بالقرب من المرآة أو بعيدًا عنها، ستتغير خصائص الصورة. على سبيل المثال، نوضح، كتمرين لاحق، أن الكائن الموضوع بين المرآة المقعرة ونقطة التركيز الخاصة بها يؤدي إلى صورة افتراضية مستقيمة وأكبر من الكائن. بالنسبة للمرآة المحدبة، تتشكل الصورة الممتدة بين النقطة البؤرية والمرآة. إنها مستقيمة بالنسبة للكائن، وهي صورة افتراضية، وهي أصغر من الكائن.
يعد تتبع الأشعة مفيدًا جدًا للمرايا. يتم تلخيص قواعد تتبع الأشعة هنا كمرجع:
- ينعكس شعاع يتحرك بالتوازي مع المحور البصري لمرآة كروية على طول خط يمر عبر النقطة البؤرية للمرآة (الشعاع 1 في الشكل\(\PageIndex{5}\)).
- ينعكس الشعاع الذي يتحرك على طول خط يمر عبر النقطة البؤرية لمرآة كروية على طول خط موازٍ للمحور البصري للمرآة (الشعاع 2 في الشكل\(\PageIndex{5}\)).
- ينعكس الشعاع الذي يتحرك على طول خط يمر عبر مركز انحناء مرآة كروية مرة أخرى على نفس الخط (الشعاع 3 في الشكل\(\PageIndex{5}\)).
- ينعكس الشعاع الذي يصطدم برأس مرآة كروية بشكل متماثل حول المحور البصري للمرآة (الشعاع 4 في الشكل\(\PageIndex{5}\)).
نستخدم تتبع الأشعة لتوضيح كيفية تكوين الصور بواسطة المرايا وللحصول على معلومات رقمية حول الخصائص البصرية للمرآة. إذا افترضنا أن المرآة صغيرة مقارنة بنصف قطر انحنائها، فيمكننا أيضًا استخدام الجبر والهندسة لاشتقاق معادلة المرآة، وهو ما نقوم به في القسم التالي. يُعد الجمع بين تتبع الأشعة ومعادلة المرآة طريقة جيدة لتحليل أنظمة المرآة.
تكوين الصورة بالانعكاس - معادلة المرآة
بالنسبة للمرآة المستوية، أظهرنا أن الصورة المتكونة لها نفس ارتفاع واتجاه الكائن، وأنها تقع على نفس المسافة خلف المرآة حيث يكون الكائن أمام المرآة. على الرغم من أن الوضع أكثر تعقيدًا بعض الشيء بالنسبة للمرايا المنحنية، فإن استخدام الهندسة يؤدي إلى صيغ بسيطة تربط مسافات الكائن والصورة بالأطوال البؤرية للمرايا المقعرة والمحدبة.
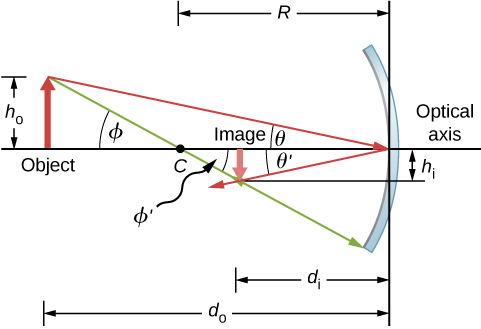
ضع في اعتبارك الكائن\(OP\) الموضح في الشكل\(\PageIndex{6}\). تم تحديد مركز انحناء المرآة\(C\) وهو على مسافة\(R\) من قمة المرآة، كما هو موضح في الشكل. يتم تسمية مسافات الكائن والصورة\(d_i\)،\(d_o\) ويتم تسمية ارتفاعات الكائن والصورة بـ\(h_o\) و\(h_i\)، على التوالي. نظرًا لأن الزوايا\(ϕ\) والزوايا الداخلية\(ϕ′\) البديلة، نعلم أن لهما نفس الحجم. ومع ذلك، يجب أن تختلف في الإشارة إذا قمنا بقياس الزوايا من المحور البصري، لذلك\(ϕ=−ϕ′\). سيناريو مماثل ينطبق على الزوايا\(θ\) و\(θ′\). يخبرنا قانون الانعكاس أن لهما نفس الحجم، ولكن يجب أن تختلف علاماتهما إذا قمنا بقياس الزوايا من المحور البصري. وهكذا،\(θ=−θ′\). أخذ مماس الزوايا\(θ\) واستخدام\(θ′\) الخاصية\(\tan(−θ)=−\tan θ\) التي تعطينا
\[\left. \begin{array}{rcl} \tanθ=\dfrac{h_o}{d_o} \\ \tanθ′=−\tanθ=\dfrac{h_i}{d_i} \end{array}\right\} =\dfrac{h_o}{d_o}=−\dfrac{h_i}{d_i} \label{eq51} \]
أو
\[- \dfrac{h_o}{h_i}=\dfrac{d_o}{d_i}.\label{eq52} \]
وبالمثل، فإن أخذ المماس\(ϕ\)\(ϕ′\) ويعطي
\[\left. \begin{array}{rcl} \tanϕ=\dfrac{h_o}{d_o-R} \\ \tanϕ′=−\tanϕ=\dfrac{h_i}{R-d_i} \end{array}\right\} =\dfrac{h_o}{d_o-R}=−\dfrac{h_i}{R-d_i} \nonumber \]
أو
\[−\dfrac{h_o}{h_i}=\dfrac{d_o-R}{R-d_i}. \label{eq55} \]
الجمع بين المعادلة\ ref {eq51} و\ ref {eq55} يعطي
\[\dfrac{d_o}{d_i}=\dfrac{d_o−R}{R−d_i}. \nonumber \]
بعد القليل من الجبر، يصبح هذا
\[\dfrac{1}{d_o}+\dfrac{1}{d_i}=\dfrac{2}{R}. \label{eq57} \]
لا يلزم تقدير تقريبي لهذه النتيجة، لذا فهي دقيقة. ومع ذلك، كما تمت مناقشته أعلاه، في التقريب ذي الزاوية الصغيرة، يكون الطول البؤري للمرآة الكروية نصف قطر انحناء المرآة، أو\(f=R/2\). إدراج هذا في المعادلة\ ref {eq57} يعطي المعادلة المتطابقة:
تربط معادلة المرآة مسافات الصورة والكائن بالمسافة البؤرية وهي صالحة فقط في تقريب الزاوية الصغيرة (المعادلة\ ref {sma}). على الرغم من أنه مشتق من مرآة مقعرة، إلا أنه ينطبق أيضًا على المرايا المحدبة (مما يثبت أن هذا يُترك كتمرين). يمكننا توسيع معادلة المرآة إلى حالة المرآة المستوية من خلال ملاحظة أن المرآة المستوية لها نصف قطر انحناء غير محدود. هذا يعني أن النقطة المحورية في اللانهاية، لذلك يتم تبسيط معادلة المرآة إلى
\[d_o=−d_i \nonumber \]
وهي نفس المعادلة التي تم الحصول عليها سابقًا.
لاحظ أننا كنا حذرين للغاية مع العلامات في اشتقاق معادلة المرآة. بالنسبة للمرآة المستوية، تحتوي مسافة الصورة على العلامة المعاكسة لمسافة الكائن. كما أن الصورة الحقيقية التي شكلتها المرآة المقعرة في الشكل\(\PageIndex{6}\) موجودة على الجانب الآخر من المحور البصري فيما يتعلق بالكائن. في هذه الحالة، يجب أن يحتوي ارتفاع الصورة على العلامة المعاكسة لارتفاع الكائن. لتتبع علامات الكميات المختلفة في معادلة المرآة، نقدم الآن اصطلاح التوقيع.
يعد استخدام اتفاقية علامة متسقة أمرًا مهمًا جدًا في البصريات الهندسية. يقوم بتعيين قيم موجبة أو سلبية للكميات التي تميز النظام البصري. يتيح لك فهم اصطلاح العلامة وصف صورة دون إنشاء مخطط شعاعي. يستخدم هذا النص اصطلاح التوقيع التالي:
- الطول البؤري إيجابي\(f\) للمرايا المقعرة وسالب للمرايا المحدبة.
- \(d_i\)مسافة الصورة إيجابية للصور الحقيقية وسلبية للصور الافتراضية.
لاحظ أن القاعدة 1 تعني أن نصف قطر انحناء المرآة الكروية يمكن أن يكون موجبًا أو سلبيًا. ماذا يعني وجود نصف قطر سالب للانحناء؟ هذا يعني ببساطة أن نصف قطر انحناء المرآة المحدبة يُعرّف بأنه سالب.
تكبير الصورة
دعونا نستخدم اصطلاح الإشارة لمزيد من تفسير اشتقاق معادلة المرآة. عند اشتقاق هذه المعادلة، وجدنا أن ارتفاعات الكائن والصورة مرتبطة بـ
\[−\dfrac{h_o}{h_i}=\dfrac{d_o}{d_i}. \label{eq61} \]
راجع المعادلة\ المرجع {eq52}. كل من الكائن والصورة التي تكوّنها المرآة في الشكل\(\PageIndex{6}\) حقيقيتان، لذا تكون مسافات الكائن والصورة موجبة. أعلى نقطة في الكائن تقع فوق المحور البصري، وبالتالي فإن ارتفاع الكائن إيجابي. ومع ذلك، تكون الصورة أسفل المحور البصري، وبالتالي يكون ارتفاع الصورة سالبًا. وبالتالي، فإن اصطلاح الإشارة هذا يتوافق مع اشتقاقنا لمعادلة المرآة.
المعادلة\ ref {eq61} تصف في الواقع التكبير الخطي (غالبًا ما يسمى ببساطة «التكبير») للصورة من حيث مسافات الكائن والصورة. وبالتالي نحدد التكبير بدون أبعاد على\(m\) النحو التالي:
\[\underbrace{m=\dfrac{h_i}{h_o}}_{\text{linear magnification}}. \label{mag} \]
\(m\)إذا كانت الصورة موجبة، تكون الصورة مستقيمة، وإذا كانت\(m\) سلبية، يتم عكس الصورة. إذا كانت\(|m|>1\) الصورة أكبر من الكائن\(|m|<1\)، وإذا كانت الصورة أصغر من الكائن. باستخدام تعريف التكبير هذا، نحصل على العلاقة التالية بين الكائن الرأسي والأفقي ومسافات الصورة:
\[m=\dfrac{h_i}{h_o}=−\dfrac{d_i}{d_o}. \nonumber \]
هذه علاقة مفيدة جدًا لأنها تتيح لك الحصول على تكبير الصورة من مسافات الكائن والصورة، والتي يمكنك الحصول عليها من معادلة المرآة.
تتضمن إحدى تقنيات الطاقة الشمسية المستخدمة اليوم لتوليد الكهرباء جهازًا (يسمى الحوض المكافئ أو المجمع المركّز) الذي يركز ضوء الشمس على أنبوب أسود يحتوي على سائل. يتم ضخ هذا السائل الساخن إلى المبادل الحراري، حيث يتم نقل الطاقة الحرارية إلى نظام آخر يستخدم لتوليد البخار وتوليد الكهرباء في نهاية المطاف من خلال دورة البخار التقليدية. \(\PageIndex{7}\)يوضح الشكل نظام العمل هذا في جنوب كاليفورنيا. المرآة الحقيقية عبارة عن أسطوانة مكافئة يقع تركيزها على الأنبوب؛ ومع ذلك، يمكننا تقريب المرآة بمقدار ربع الأسطوانة الدائرية بالضبط.

- إذا أردنا تركيز أشعة الشمس على مسافة ٤٠٫٠ سم من المرآة، فما نصف قطر المرآة؟
- ما مقدار ضوء الشمس المركّز على الأنبوب، لكل متر من طول الأنبوب، بافتراض أن التشمس (الإشعاع الشمسي الساقط) يساوي 900 واط/م 2؟
- إذا كان قطر الأنبوب الحامل للسوائل 2.00 سم، فما مقدار الزيادة في درجة حرارة السائل لكل متر من الأنبوب خلال مدة دقيقة واحدة؟ افترض أن كل الإشعاع الشمسي الساقط على العاكس يمتصه الأنبوب، وأن السائل عبارة عن زيت معدني.
إستراتيجية
حدد أولاً المبادئ الفيزيائية المعنية. يتعلق الجزء (أ) ببصريات المرايا الكروية. يتضمن الجزء (ب) القليل من الرياضيات، وفي المقام الأول الهندسة. يتطلب الجزء (ج) فهمًا للحرارة والكثافة.
الحل
أ- الشمس هي الجسم، وبالتالي فإن مسافة الكائن هي في الأساس اللانهاية:\(d_o=\infty\). مسافة الصورة المطلوبة هي\(d_i=40.0\,cm\). نستخدم معادلة المرآة (المعادلة\ ref {معادلة المرآة}) للعثور على الطول البؤري للمرآة:
\[\begin{align*} \dfrac{1}{d_o}+\dfrac{1}{d_i} &=\dfrac{1}{f} \nonumber \\[4pt] f &= \left(\dfrac{1}{d_o}+\dfrac{1}{d_i}\right)^{−1} \\[4pt] &= \left(\dfrac{1}{\infty}+\dfrac{1}{40.0\,cm}\right)^{−1} \\[4pt] &= 40.0 \,cm \end{align*} \nonumber \]
وبالتالي، فإن نصف قطر المرآة هو
\[R=2f=80.0\,cm. \nonumber \]
ب- العزل هو 900 واط/م 2. يجب أن تجد مساحة\(A\) المقطع العرضي للمرآة المقعرة، نظرًا لأن الطاقة التي يتم توصيلها هي\(900\, W/m^2×A\). المرآة في هذه الحالة هي ربع مقطع من الأسطوانة، وبالتالي فإن مساحة\(L\) طول المرآة هي\(A=\frac{1}{4}(2πR)L\). ثم تكون المساحة التي يبلغ طولها 1.00 متر هي
\[\begin{align*} A&=\dfrac{\pi}{2}R(1.00m) \\[4pt] &=\dfrac{(3.14)}{2}(0.800\,m)(1.00\,m) \\[4pt] &=1.26\,m^2. \end{align*} \nonumber \]
يتم بعد ذلك التشمس على طول الأنبوب الذي يبلغ طوله 1.00 متر
\[(9.00×10^2\dfrac{W}{m^2})(1.26\,m^2)=1130\,W. \nonumber \]
ج- يتم إعطاء الزيادة في درجة الحرارة من خلال\(Q=mcΔT\). كتلة\(m\) الزيت المعدني في قسم الأنبوب الذي يبلغ طوله متر واحد
\[ \begin{align*} m &= ρV = ρπ\left(\dfrac{d}{2}\right)^2(1.00\,m) \nonumber \\[4pt] &=(8.00×10^2kg/m^3)(3.14)(0.0100\,m)^2(1.00\,m) \nonumber \\[4pt] &=0.251\,kg \end{align*} \nonumber \]
لذلك، فإن الزيادة في درجة الحرارة في دقيقة واحدة هي
\[ \begin{align*} \Delta T&= \dfrac{Q}{mc} \nonumber \\[4pt] &=\dfrac{(1130\,W)(60.0\,s)}{(0.251\,kg)(1670\,J⋅kg/°C)} \nonumber \\[4pt] &=162°\end{align*} \nonumber \]
الدلالة
يمكن لمجموعة من هذه الأنابيب في صحراء كاليفورنيا أن توفر إنتاجًا حراريًا يبلغ 250 ميجاوات في يوم مشمس، مع وصول السوائل إلى درجات حرارة تصل إلى 400 درجة مئوية، ونحن ندرس مترًا واحدًا فقط من الأنابيب هنا ونتجاهل فقدان الحرارة على طول الأنبوب.
مقياس القرنية هو جهاز يستخدم لقياس انحناء قرنية العين، وخاصة لتركيب العدسات اللاصقة. ينعكس الضوء من القرنية، التي تعمل كمرآة محدبة، ويقيس مقياس القرنية تكبير الصورة. كلما كان التكبير أصغر، كلما قل نصف قطر انحناء القرنية. إذا كان مصدر الضوء على بُعد 12 سم من القرنية وكانت نسبة تكبير الصورة 0.032، فما نصف قطر انحناء القرنية؟
إستراتيجية
إذا وجدت الطول البؤري للمرآة المحدبة التي شكلتها القرنية، فأنت تعرف نصف قطر الانحناء (وهو ضعف الطول البؤري). مسافة الكائن هي d o = 12 سم والتكبير هو m=0.032. ابحث أولاً عن مسافة الصورة\(d_i\) ثم قم بحل البعد البؤري\(f\).
الحل
ابدأ بمعادلة التكبير (المعادلة\ ref {mag}) وحل عوائد القيم المعطاة وإدخالها\(d_i\)
\[d_i=−m d_o=−(0.032)(12\,cm)=−0.384\,cm \nonumber \]
حيث احتفظنا برقم مهم إضافي لأن هذه خطوة وسيطة في الحساب. حل معادلة المرآة للطول البؤري\(f\) وأدخل القيم المعروفة لمسافات الكائن والصورة. النتيجة هي
\[ \begin{align*} \dfrac{1}{d_o}+\dfrac{1}{d_i} &= \dfrac{1}{f} \\[4pt] f &= \left(\dfrac{1}{d_o}+\dfrac{1}{d_i}\right)^{−1} \\[4pt] &= \left(\dfrac{1}{12cm}+\dfrac{1}{-0.384cm}\right)^{−1} \\[4pt] &=-40.0 \,cm \end{align*} \nonumber \]
نصف قطر الانحناء هو ضعف البعد البؤري، لذلك
\[R=2f=−0.80\,cm \nonumber \]
الدلالة
البعد البؤري سالب، لذا يكون التركيز افتراضيًا، كما هو متوقع للمرآة المقعرة والجسم الحقيقي. إن نصف قطر الانحناء الموجود هنا معقول للقرنية. تبلغ المسافة من القرنية إلى الشبكية في عين البالغين حوالي 2.0 سم. من الناحية العملية، قد لا تكون القرنيات كروية، مما يعقد مهمة تركيب العدسات اللاصقة. لاحظ أن مسافة الصورة هنا سلبية، بما يتفق مع حقيقة أن الصورة خلف المرآة. وبالتالي، تكون الصورة افتراضية لأنه لا توجد أشعة تمر عبرها فعليًا. في المشكلات والتمارين، ستوضح أنه بالنسبة لمسافة الجسم الثابتة، فإن نصف قطر الانحناء الأصغر يتوافق مع التكبير الأصغر.
- الخطوة 1. تأكد أولاً من تضمين تكوين الصورة بواسطة مرآة كروية.
- الخطوة 2. حدد ما إذا كان تتبع الشعاع أو معادلة المرآة أو كليهما مطلوبًا. يعد الرسم مفيدًا جدًا حتى إذا لم تكن المشكلة تتطلب تتبع الأشعة على وجه التحديد. اكتب الرموز والقيم المعروفة على الرسم.
- الخطوة 3. حدد بالضبط ما يجب تحديده في المشكلة (حدد المجهول).
- الخطوة 4. قم بعمل قائمة بما هو معطى أو يمكن استنتاجه من المشكلة كما هو مذكور (حدد المعروف).
- الخطوة 5. إذا كان تتبع الأشعة مطلوبًا، فاستخدم قواعد تتبع الأشعة المدرجة بالقرب من بداية هذا القسم.
- الخطوة 6. تتطلب معظم المشاكل الكمية استخدام معادلة المرآة. استخدم الأمثلة كأدلة لاستخدام معادلة المرآة.
- الخطوة 7. تحقق لمعرفة ما إذا كانت الإجابة منطقية. هل تتوافق علامات مسافة الكائن ومسافة الصورة والطول البؤري مع ما هو متوقع من تتبع الأشعة؟ هل علامة التكبير صحيحة؟ هل مسافات الكائن والصورة معقولة؟
الابتعاد عن تقريب الزاوية الصغيرة
يُعد تقريب الزاوية الصغيرة (Equal\ ref {smallangle}) حجر الزاوية في المناقشة السابقة لتكوين الصورة بواسطة مرآة كروية. عند انتهاك هذا التقريب، تصبح الصورة التي تم إنشاؤها بواسطة مرآة كروية مشوهة. هذا التشويه يسمى الانحراف. نناقش هنا بإيجاز نوعين محددين من الانحرافات: الانحراف الكروي والغيبوبة.
انحراف كروي
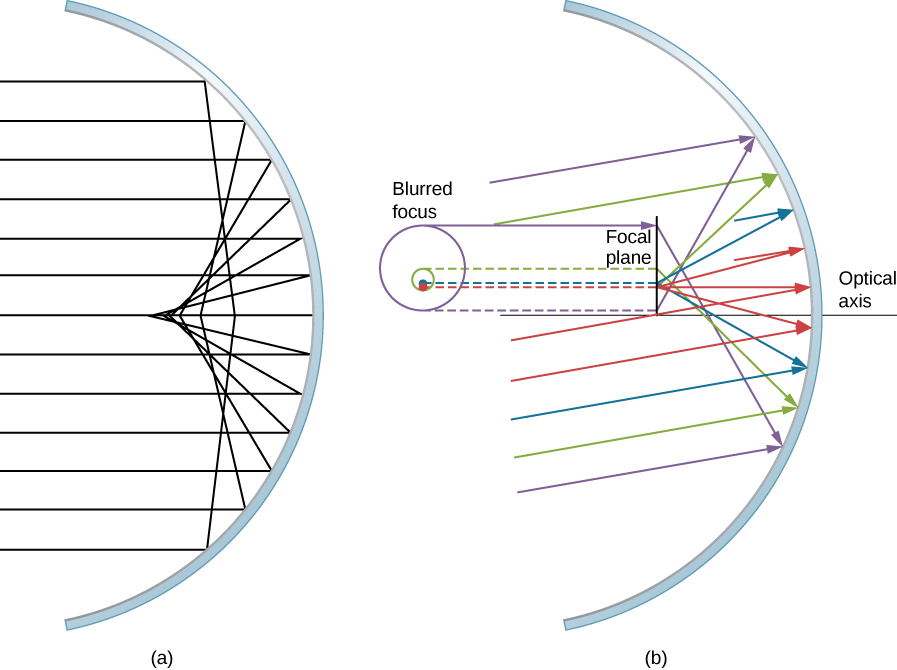
خذ بعين الاعتبار شعاعًا عريضًا من الأشعة المتوازية يؤثر على مرآة كروية، كما هو موضح في الشكل\(\PageIndex{8}\). كلما ابتعدت الأشعة عن المحور البصري، كلما اقتربت المرآة الكروية من مرآة مكافئة. وبالتالي، لا تركز هذه الأشعة في نفس نقطة الأشعة القريبة من المحور البصري، كما هو موضح في الشكل. بسبب الانحراف الكروي، ستصبح صورة جسم ممتد في مرآة كروية غير واضحة. تعتبر الانحرافات الكروية من سمات المرايا والعدسات التي نأخذها في الاعتبار في القسم التالي من هذا الفصل (هناك حاجة إلى مرايا وعدسات أكثر تطوراً للقضاء على الانحرافات الكروية).
الغيبوبة أو الانحراف الكوماتي
تشبه الغيبوبة الانحراف الكروي، ولكنها تنشأ عندما لا تكون الأشعة الواردة موازية للمحور البصري، كما هو موضح في الشكل\(\PageIndex{8b}\). تذكر أن تقريب الزاوية الصغيرة ينطبق على المرايا الكروية الصغيرة مقارنة بنصف قطرها. في هذه الحالة، تعتبر المرايا الكروية تقديرات تقريبية جيدة للمرايا المكافئة. تقوم المرايا المكافئة بتركيز جميع الأشعة الموازية للمحور البصري عند النقطة البؤرية. ومع ذلك، فإن الأشعة المتوازية غير الموازية للمحور البصري تتركز على ارتفاعات مختلفة وعلى أطوال بؤرية مختلفة، كما هو موضح في الشكل\(\PageIndex{8b}\). نظرًا لأن المرآة الكروية متماثلة حول المحور البصري، فإن الأشعة الملونة المختلفة في هذا الشكل تخلق دوائر من اللون المقابل على المستوى البؤري.
على الرغم من أن المرآة الكروية موضحة في الشكل\(\PageIndex{8b}\)، إلا أن الانحراف الكوماتي يحدث أيضًا للمرايا المكافئة - فهو لا ينتج عن انهيار في تقريب الزاوية الصغيرة (المعادلة\ ref {smallangle}). ومع ذلك، يحدث الانحراف الكروي فقط للمرايا الكروية وينتج عن انهيار تقريب الزاوية الصغيرة. سنناقش كل من الغيبوبة والانحراف الكروي لاحقًا في هذا الفصل، فيما يتعلق بالتلسكوبات.


