16E: الأمواج (التمارين)

أسئلة مفاهيمية

16.1 موجات السفر

1. أعط مثالًا واحدًا للموجة العرضية ومثالًا واحدًا للموجة الطولية، مع الحرص على ملاحظة الاتجاهات النسبية للاضطراب وانتشار الموجة في كل منهما.
2. طول موجة عرضية جيبية يبلغ طولها الموجي ٢٫٨٠ م، ويستغرق جزء من الخيط عند الموضع x الانتقال من الموضع الأقصى y = 0.03 m إلى موضع الاتزان y = 0. ما الفترة والتردد وسرعة الموجة للموجة؟
3. ما الفرق بين سرعة الانتشار وتردد الموجة الميكانيكية؟ هل يؤثر أحدهما أو كلاهما على الطول الموجي؟ إذا كان الأمر كذلك، كيف؟
4. ضع في اعتبارك نبعًا ممتدًا، مثل الزنبرك اللامع. يمكن أن يدعم الزنبرك الممتد الموجات الطولية والموجات العرضية. كيف يمكنك إنتاج موجات عرضية في الربيع؟ كيف يمكنك إنتاج موجات طولية في الربيع؟
5. ضع في اعتبارك الموجة التي يتم إنتاجها على زنبرك ممتد عن طريق الإمساك بأحد طرفيها وهزها لأعلى ولأسفل. هل يعتمد الطول الموجي على المسافة التي تحرك فيها يدك لأعلى ولأسفل؟
6. تُنتَج موجة جيبية عرضية على زنبرك ممتد له نقطة T. يتحرك كل قسم من الزنبرك عموديًا على اتجاه انتشار الموجة، بحركة توافقية بسيطة بسعة A. هل يتذبذب كل قسم بنفس فترة الموجة أم بفترة مختلفة؟ إذا تضاعفت سعة الموجة العرضية وبقيت الفترة كما هي، فهل ستكون إجابتك هي نفسها؟
7. لا تتطلب الموجة الكهرومغناطيسية، مثل الضوء، وسيطًا. هل يمكنك التفكير في مثال يدعم هذا الادعاء؟

16.2 رياضيات الأمواج

8. إذا كان عليك هز نهاية الزنبرك المشدود لأعلى ولأسفل 10 مرات في الثانية، فما وتيرة وفترة الموجة الجيبية الناتجة عن الزنبرك؟
9. إذا قمت بهز نهاية الزنبرك الممتد لأعلى ولأسفل بتردد f، يمكنك إنتاج موجة جيبية عرضية تنتشر أسفل الزنبرك. هل يعتمد رقم الموجة على التردد الذي تهز فيه الزنبرك؟
10. هل تعتمد السرعة الرأسية لجزء من الخيط الأفقي المشدود الذي تنتشر من خلاله الموجة الجيبية والعرضية على سرعة موجة الموجة العرضية؟
11. في هذا القسم، درسنا الموجات التي تتحرك بسرعة موجة ثابتة. هل تتسارع الوسيلة؟
12. إذا أسقطت حصاة في بركة، فقد تلاحظ إنتاج عدة تموجات متحدة المركز، وليس مجرد تموج واحد. لماذا تعتقد ذلك?

16.3 سرعة الموجة على خيط ممتد

13. إذا زاد الشد في الخيط بعامل أربعة، فبأي عامل تزيد سرعة موجة الموجة على الوتر؟
14. هل تتحرك الموجة الصوتية بشكل أسرع في مياه البحر أو المياه العذبة، إذا كانت مياه البحر والمياه العذبة في نفس درجة الحرارة وكانت الموجة الصوتية تتحرك بالقرب من السطح؟ $$\ rho_ {w}\ حوالي 1000\؛ كغم/م^ {3}،\ rho_ {s}\ حوالي 1030\؛ كغم/م^ {3}، B_ {w} = 2.15\ مرة 10 ^ {9}\؛ Pa، B_ {s} = 2.34\ مرات 10^ {9}\؛ Pa$$
15. تحتوي القيثارات على سلاسل ذات كثافة كتلة خطية مختلفة. إذا كانت السلسلة الأقل كثافة والسلسلة الأعلى كثافة تحت نفس الشد، فما الخيط الذي سيدعم الموجات ذات سرعة الموجة الأعلى؟
16. تظهر أدناه ثلاث موجات تم إرسالها عبر سلسلة في أوقات مختلفة. يظل التوتر في السلسلة ثابتًا. (أ) رتب الموجات من أصغر طول موجي إلى أكبر طول موجي. (ب) رتب الموجات من أدنى تردد إلى أعلى تردد.

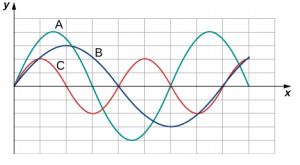
17. أحيانًا ما تُسمع خطوط الطاقة الكهربائية المتصلة بقطبي المرافق وهي تصدر صوتًا عند دفعها إلى التذبذب بفعل الرياح. تعتمد سرعة الموجات على خطوط الطاقة على التوتر. ما الذي يوفر التوتر في خطوط الطاقة؟
18. يتم تقسيم سلسلتين، واحدة ذات كثافة كتلة منخفضة والأخرى ذات كثافة خطية عالية معًا. يتم ربط الطرف ذو الكثافة الأعلى بمنشور معمل ويحمل الطالب الطرف الحر من سلسلة الكثافة ذات الكتلة المنخفضة. يقوم الطالب بتدوير الخيط وإرسال نبضة إلى أسفل الأوتار. إذا كان الشد هو نفسه في كلتا السلسلتين، فهل تنتقل النبضة بنفس سرعة الموجة في كلتا السلسلتين؟ إذا لم يكن الأمر كذلك، فأين تنتقل بشكل أسرع، في السلسلة منخفضة الكثافة أو السلسلة عالية الكثافة؟

16.4 طاقة الموجة وقوتها

19. ضع في اعتبارك خيطًا تحت التوتر بكثافة كتلة خطية ثابتة. موجة جيبية ذات تردد زاوي وسعة تنتجها بعض القوى الدافعة الخارجية. إذا انخفض تردد القوة الدافعة إلى نصف التردد الأصلي، فكيف تتأثر القدرة المتوسطة الزمنية للموجة؟ إذا انخفضت سعة القوة الدافعة بمقدار النصف، فكيف تتأثر القدرة المتوسطة الزمنية؟ اشرح إجابتك.
20. تنخفض موجات الماء الدائرية في السعة عندما تبتعد عن مكان سقوط الصخور. اشرح لماذا.
21. في الموجة العرضية على الخيط، تكون حركة الخيط متعامدة مع حركة الموجة. إذا كان الأمر كذلك، فكيف يمكن تحريك الطاقة على طول الخيط؟
22. تعمل الطاقة من الشمس على تدفئة جزء الأرض الذي يواجه الشمس خلال ساعات النهار. لماذا يكون القطبان الشمالي والجنوبي باردًا بينما خط الاستواء دافئ جدًا؟
23. تنخفض شدة الموجات الكروية عندما تتحرك الموجة بعيدًا عن المصدر. إذا كانت شدة الموجة عند المصدر هي I ₀، فما المسافة من المصدر التي ستنخفض شدتها بعامل تسعة؟

16.5 تداخل الموجات

24. يتم إرسال موجة جيبية ساقطة على طول خيط مثبت على الحائط بسرعة موجة v. تنعكس الموجة من نهاية الخيط. وصف الموجة المنعكسة.
25. خيط طوله 2.00 متر وكثافته الكتلية الخطية\(\mu\) = 0.006 كغم/متر موصولة بنهاية خيط طوله 2.00 متر بكثافة كتلته الخطية\(\mu\) = 0.012 كجم/م، ويتم تثبيت الطرف الحر من السلسلة ذات الكثافة العالية بالجدار، ويحمل الطالب الطرف الحر للخيط منخفض الكثافة، الحفاظ على التوتر ثابتًا في كلا السلسلتين. يقوم الطالب بإرسال نبضة إلى أسفل الخيط. وصف ما يحدث في الواجهة بين السلسلتين.
26. يقام زنبرك طويل ضيق من قبل طالبين، طالب واحد يحمل كل طرف. يعطي كل طالب نهايته قلبًا مرسلًا طولًا موجيًا واحدًا من الموجة الجيبية إلى أسفل الزنبرك في اتجاهين متعاكسين. عندما تلتقي الأمواج في المنتصف، كيف تبدو الموجة؟
27. العديد من الموضوعات التي تمت مناقشتها في هذا الفصل مفيدة بخلاف موضوعات الموجات الميكانيكية. من الصعب تصور موجة ميكانيكية ذات زوايا حادة، ولكن قد تواجه مثل هذا الشكل الموجي في فئة الإلكترونيات الرقمية الخاصة بك، كما هو موضح أدناه. قد تكون هذه إشارة من جهاز يعرف باسم المحول التناظري إلى الرقمي، حيث يتم تحويل إشارة الجهد المستمر إلى إشارة منفصلة أو تسجيل رقمي للصوت. ما ناتج تراكب الإشارتين؟

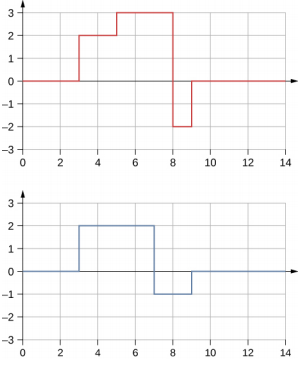
28. يتم تثبيت سلسلة ذات كثافة كتلة خطية ثابتة بإحكام بواسطة طالبين، كل منهما يحمل أحد طرفيه. التوتر في السلسلة ثابت. يقوم كل طالب بإرسال موجات إلى أسفل السلسلة عن طريق تحريك السلسلة. (أ) هل من الممكن أن تكون للموجات سرعات موجية مختلفة؟ (ب) هل من الممكن أن تكون للموجات ترددات مختلفة؟ (ج) هل من الممكن أن تكون للموجات أطوال موجية مختلفة؟

16.6 الموجات الدائمة والرنين

29. وجدت إحدى الشركات المصنعة للشاحنات أن الدعامة الموجودة في المحرك تتعطل قبل الأوان. يحدد مهندس الصوت أن الدعامة يتردد صداها عند تردد المحرك ويشتبه في أن هذه قد تكون المشكلة. ما الخاصيتان المحتملتان للدعامة التي يمكن تعديلهما لتصحيح المشكلة؟
30. لماذا يبدو أن أسطح الصالات الرياضية والكنائس تفشل أكثر من المنازل العائلية عند حدوث زلزال؟
31. يمكن ضبط أكواب النبيذ بالرنين عن طريق ترطيب إصبعك وفركه حول حافة الزجاج. لماذا؟
32. يتم وضع وحدات تكييف الهواء أحيانًا على سطح المنازل في المدينة. من حين لآخر، تسبب مكيفات الهواء همهمة غير مرغوب فيها في جميع أنحاء الطوابق العليا من المنازل. لماذا يحدث هذا؟ ما الذي يمكن فعله لتقليل الطنين؟
33. خذ بعين الاعتبار الموجة الواقفة على غرار y (x, t) = 4.00 سم sin (3 م ⁻¹ x) cos (4 s ⁻¹ t). هل هناك عقدة أو مضاد في x = 0.00 m؟ ماذا عن الموجة الواقفة على غرار y (x، t) = خطيئة 4.00 سم (3 م ⁻¹ x +\(\frac{\pi}{2}\)) cos (4 ث ⁻¹ t)؟ هل هناك عقدة أو مضاد في موضع x = 0.00 m؟

مشاكل

16.1 موجات السفر

34. يمكن للعواصف في جنوب المحيط الهادئ أن تخلق موجات تنتقل على طول الطريق إلى ساحل كاليفورنيا، على بعد 12,000 كم. ما المدة التي تستغرقها هذه المسافة إذا سافرت بسرعة ١٥٫٠ م/ث؟
35. تنتشر الموجات فوق حوض السباحة بسرعة 0.75 متر/ثانية، حيث تقوم برش الماء من أحد طرفي حوض السباحة وتلاحظ أن الموجة تتجه إلى الطرف المقابل، وتنعكس، وتعود في غضون 30.00 ثانية، فما مدى بُعد الطرف الآخر من حوض السباحة؟
36. تُحدث الرياح تموجات فوق المحيط يبلغ طولها الموجي ٥٫٠٠ سم وتنتشر بسرعة ٢٫٠٠ م/ث، فما ترددها؟
37. ما عدد المرات التي يتحرك فيها قارب لأعلى ولأسفل في الدقيقة فوق أمواج المحيط التي يبلغ طولها الموجي ٤٠٫٠ م وسرعة انتشارها ٥٫٠٠ م/ث؟
38. يهز الكشافة في المخيم جسر الحبل الذي عبروه للتو ويلاحظون قمم الأمواج على بعد 8.00 أمتار. إذا هزت هذه الموجات الجسر مرتين في الثانية، فما سرعة انتشار الموجات؟
39. ما الطول الموجي للموجات التي تكوِّنها في حوض سباحة إذا رشت يدك بمعدل 2.00 هرتز وانتشرت الموجات بسرعة مقدارها 0.800 متر/ثانية؟
40. ما الطول الموجي لزلزال يهزك بتردد 10.0 هرتز ويصل إلى مدينة أخرى على بُعد 84.0 كم في 12.0 ثانية؟
41. يبلغ طول موجة موجات الراديو المرسلة عبر الفضاء الفارغ بسرعة الضوء (v = c = 3.00 x 10 ⁸ m/s) بواسطة المركبة الفضائية Voyager 0.120 m، ما ترددها؟
42. أذنك قادرة على تمييز الأصوات التي تصل إلى كل أذن بفارق 0.34 مللي ثانية فقط، وهو أمر مفيد في تحديد مصدر الصوت منخفض التردد. (أ) لنفترض أن مصدر صوت منخفض التردد قد وُضِع على يمين شخص تبعد أذنيه مسافة 18 سم تقريبًا، وأن سرعة الصوت المتولد تبلغ 340 متر/ثانية، فما طول الفاصل الزمني بين وصول الصوت إلى الأذن اليمنى ووصول الصوت إلى الأذن اليسرى؟ (ب) لنفترض أن الشخص نفسه كان يمارس رياضة الغطس وأن مصدر الصوت منخفض التردد كان على يمين الغواص. ما المدة الفاصلة بين وصول الصوت إلى الأذن اليمنى ووصول الصوت إلى الأذن اليسرى، إذا كانت سرعة الصوت في الماء 1500 متر/ثانية؟ (ج) ما أهمية الفاصل الزمني بين الحالتين؟
43. (أ) تقيس أجهزة قياس الزلازل أوقات وصول الزلازل بدقة تبلغ 0.100 ثانية، ولتحديد المسافة إلى مركز الزلزال، يقارن الجيولوجيون أوقات وصول الموجات S و P التي تنتقل بسرعات مختلفة. إذا انتقلت الموجات S- و P بسرعة 4.00 و 7.20 كم/ثانية، على التوالي، في المنطقة قيد النظر، فما مدى دقة تحديد المسافة إلى مصدر الزلزال؟ (ب) يمكن استخدام الموجات الزلزالية الناتجة عن التفجيرات الجوفية للقنابل النووية لتحديد موقع الاختبار والكشف عن انتهاكات حظر التجارب. ناقش ما إذا كانت إجابتك على (أ) تعني حدًا خطيرًا لهذا الاكتشاف. (لاحظ أيضًا أن عدم اليقين يكون أكبر إذا كان هناك عدم يقين في سرعات انتشار الموجات S- و P.)
44. تقوم إحدى فتيات الكشافة بنزهة لمسافة 10.00 كم للحصول على شارة الجدارة. بينما كانت في نزهة على الأقدام، ترى جرفًا على بعد مسافة. إنها ترغب في تقدير الوقت اللازم للمشي إلى الجرف. إنها تعرف أن سرعة الصوت تبلغ حوالي 343 مترًا في الثانية. تصرخ وتجد أن الصدى يعود بعد حوالي 2.00 ثانية. إذا تمكنت من المشي لمسافة 1.00 كم في 10 دقائق، فما المدة التي ستستغرقها للوصول إلى الجرف؟
45. يُطلب من مهندس ضمان الجودة في شركة مقلاة تأهيل خط جديد من أواني القلي غير المطلية بالالتصاق. يجب أن يكون سمك الطلاء 1.00 مم. تتمثل إحدى طرق اختبار السماكة في أن يختار المهندس نسبة مئوية من الأحواض المصنعة، ويزيل الطلاء، ويقيس السماكة باستخدام ميكرومتر. هذه الطريقة هي طريقة اختبار مدمرة. بدلاً من ذلك، يقرر المهندس أنه سيتم اختبار كل مقلاة باستخدام طريقة غير مدمرة. يتم استخدام محول الموجات فوق الصوتية الذي ينتج موجات صوتية بتردد f = 25 كيلو هرتز. يتم إرسال الموجات الصوتية من خلال الطلاء وتنعكس من خلال الواجهة بين الطلاء والوعاء المعدني، ويتم تسجيل الوقت. الطول الموجي للموجات فوق الصوتية في الطلاء هو 0.076 م، ما الوقت الذي يجب تسجيله إذا كان الطلاء هو السماكة الصحيحة (1.00 مم)؟

16.2 رياضيات الأمواج

46. يمكن وصف النبض بأنه اضطراب أحادي الموجة يتحرك عبر وسيط. ضع في اعتبارك نبضة تم تعريفها في الوقت t = 0.00 ثانية بالمعادلة y (x) =\(\frac{6.00\; m^{3}}{x^{2} + 2.00\; m^{2}}\) تتمركز حول x = 0.00 m، وتتحرك النبضة بسرعة v = 3.00 m/s في اتجاه x الموجب. (أ) ما سعة النبض؟ (ب) ما معادلة النبض كدالة للموضع والزمن؟ (ج) أين تتمركز النبضة في الوقت t = 5.00 ثانية؟
47. تم تصميم موجة عرضية على خيط باستخدام دالة الموجة y (x، t) = (0.20 سم) sin (2.00 m ⁻¹ x − 3.00 s ⁻¹ t +\(\frac{\pi}{16}\)). ما ارتفاع الخيط بالنسبة إلى موضع الاتزان عند الموضع x = 4.00 m والوقت t = 10.00 s؟
48. ضع في اعتبارك دالة الموجة y (x، t) = زاوية (3.00 سم) (0.4 م ⁻¹ x + 2.00 ثانية ⁻¹ t +\(\frac{\pi}{10}\)). ما الفترة والطول الموجي والسرعة والتحول الطوري الأولي للموجة على غرار دالة الموجة؟
49. يتم تعريف النبض على أنه y (x، t) =\(e ^{−2.77 \left(\dfrac{2.00(x − 2.00\; m/s(t))}{5.00\; m}\right)^{2}}\). استخدم جدول بيانات، أو برنامج كمبيوتر آخر، لرسم النبض على أنه ارتفاع المتوسط y كدالة للموضع x. ارسم النبض في بعض الأحيان t = 0.00 ثانية و t = 3.00 ثانية على نفس الرسم البياني. أين تتمركز النبضة في الوقت t = 3.00 ثانية؟ استخدم جدول البيانات الخاص بك للتحقق من إجابتك.
50. يتم تصميم الموجة في الوقت t = 0.00 ثانية باستخدام دالة الموجة التي تعتمد على الموضع. المعادلة هي y (x) = (0.30 م) الخطيئة (6.28 م ⁻¹ x). تنتقل الموجة لمسافة 4.00 أمتار في 0.50 ثانية في الاتجاه السيني الموجب. اكتب معادلة للموجة كدالة للموضع والوقت.
51. صُمِّمت موجة باستخدام الدالة y (x، t) = (0.25 م) cos (0.30 م ⁻¹ x − 0.90 ثانية ⁻¹ t +\(\frac{\pi}{3}\)). أوجد (أ) السعة، (ب) رقم الموجة، (ج) التردد الزاوي، (د) سرعة الموجة، (هـ) تحول الطور الأولي، (f) الطول الموجي، (ز) فترة الموجة.
52. تبلغ سعة موجة سطح المحيط ٠٫٦٠ م، والمسافة من الحوض إلى القاع ٨٫٠٠ م، وتتحرَّك بسرعة موجية ثابتة مقدارها ١٫٥٠ م/ث وتنتشر في الاتجاه السيني الموجب. عند t = 0، تكون إزاحة الماء عند x = 0 صفرًا، و vy إيجابية. (أ) بافتراض إمكانية تشكيل الموجة كموجة جيبية، اكتب دالة الموجة لنمذجة الموجة. (ب) استخدم جدول بيانات لرسم دالة الموجة في بعض الأحيان t = 0.00 ثانية و t = 2.00 ثانية على نفس الرسم البياني. تحقق من أن الموجة تتحرك لمسافة 3.00 م في تلك الـ 2.00 ثانية.
53. يتم تصميم الموجة بواسطة دالة الموجة y (x، t) = (0.30 m) sin\(\Big[ \frac{2 \pi}{4.50\; m} (x − 18.00\; m/s\; t) \Big]\). ما السعة والطول الموجي وسرعة الموجة والفترة والتردد للموجة؟
54. وُصفت موجة عرضية على خيط باستخدام دالة الموجة y (x, t) = (0.50 سم) sin (1.57 m ⁻¹ x − 6.28 s ⁻¹ t). (أ) ما هي السرعة الموجية للموجة؟ (ب) ما مقدار السرعة القصوى للخيط العمودي على اتجاه الحركة؟
55. يلاحظ السباح في المحيط يومًا ما أن موجات سطح المحيط دورية وتشبه الموجة الجيبية. يقدر السباح أن المسافة الرأسية بين القمة وقاع كل موجة تبلغ حوالي 0.45 متر، والمسافة بين كل قمة حوالي 1.8 متر، ويحسب السباح أن 12 موجة تمر كل دقيقتين. حدد دالة الموجة التوافقية البسيطة التي تصف هذه الموجات.
56. خذ بعين الاعتبار الموجة التي وصفتها دالة الموجة y (x، t) = 0.3 م sin (2.00 م ⁻¹ x − 628.00 s ⁻¹ t). (أ) كم عدد القمم التي يمر بها مراقب في موقع ثابت في دقيقتين ونصف؟ (ب) إلى أي مدى قطعتها الموجة في ذلك الوقت؟
57. ضع في اعتبارك موجتين تحددهما وظائف الموجة y ₁ (x، t) = 0.50 m sin\(\left(\dfrac{2 \pi}{3.00\; m}x + \dfrac{2 \pi}{4.00\; s}t \right)\) و y ₂ (x، t) = 0.50 m sin\(\left(\dfrac{2 \pi}{6.00\; m}x − \dfrac{2 \pi}{4.00\; s}t \right)\). ما هي أوجه التشابه والاختلاف بين الموجتين؟
58. ضع في اعتبارك موجتين تحددهما وظائف الموجة y ₁ (x، t) = 0.20 م sin\(\left(\dfrac{2 \pi}{6.00\; m}x − \dfrac{2 \pi}{4.00\; s}t \right)\) و y ₂ (x، t) = 0.20 m cos\(\left(\dfrac{2 \pi}{6.00\; m}x − \dfrac{2 \pi}{4.00\; s}t \right)\). ما هي أوجه التشابه والاختلاف بين الموجتين؟
59. سرعة موجة عرضية على خيط تساوي 300.00 م/ث، وطولها الموجي ٠٫٥٠ م، والسعة ٢٠٫٠٠ سم. ما مقدار الوقت اللازم لجسيم على الخيط لكي يتحرك عبر مسافة ٥٫٠٠ كم؟

16.3 سرعة الموجة على خيط ممتد

60. تُرسل الموجات العرضية على طول خيط طوله ٥٫٠٠ متر بسرعة ٣٠٫٠٠ م/ث، ويقع الخيط تحت شدٍّ مقداره ١٠٫٠٠ نيوتن. ما كتلة الوتر؟
61. سلك نحاسي بكثافة\(\rho\) = 8920 كجم/م ³، ونصف قطره 1.20 مم، وطوله L. يتم تثبيت السلك تحت توتر قدره 10.00 نيوتن. يتم إرسال الموجات العرضية إلى أسفل السلك. (أ) ما كثافة الكتلة الخطية للسلك؟ (ب) ما سرعة الموجات عبر السلك؟
62. كثافة كتلة خطية لسلك بيانو\(\mu\) = 4.95 x 10 ⁻³ kg/m، وتحت أي شد يجب الاحتفاظ بالخيط لإنتاج موجات بسرعة موجية مقدارها 500.00 m/s؟
63. تم ربط خيط بكثافة كتلته الخطية\(\mu\) = 0.0060 كجم/م بالسقف. ترتبط كتلة وزنها 20 كجم بالنهاية الحرة للخيط. يتم سحب الخيط، مما يؤدي إلى إرسال نبضة إلى أسفل الخيط. قم بتقدير سرعة النبض أثناء تحركه لأسفل السلسلة.
64. يبلغ طول السلك ثلاثة أمتار بكثافة كتلته الخطية\(\mu\) = 0.0075 كغم/متر. يتم سحب السلك ويستغرق الأمر 0.20 ثانية حتى تصل النبضة إلى نهاية الخيط. ما مقدار الشد في الخيط؟
65. خيط طوله ٣٫٠٠ م وكتلته ٥٫٠٠ جم، ويُثبَت الخيط مشدودًا بشدٍّ مقداره ٥٠٠.٠٠ نيوتن على الوتر. يتم إرسال نبضة إلى أسفل السلسلة. ما المدة التي تستغرقها النبضة للانتقال لمسافة ٣٫٠٠ م من الخيط؟
66. تنتقل موجة صوتية عبر عمود من النيتروجين في STP. بافتراض الكثافة\(\rho\) = 1.25 كجم/م ³ ومعامل الكتلة\(\beta\) = 1.42 x 10 ⁵ Pa، ما السرعة التقريبية للموجة الصوتية؟
67. ما السرعة التقريبية للصوت المنتقل عبر الهواء عند درجة حرارة T = 28°س؟
68. تنتقل الموجات العرضية عبر خيط يساوي الشد ٧٫٠٠ نيوتن بسرعة ٢٠٫٠٠ م/ث. ما مقدار الشد المطلوب لسرعة موجة مقدارها ٢٥٫٠٠ م/ث؟
69. يتم ربط سلسلتين بين قطبين يفصل بينهما مسافة 2.00 متر كما هو موضح أدناه، وكلاهما تحت نفس الشد البالغ 600.00 N. السلسلة 1 لها كثافة خطية تبلغ\(\mu_{1}\) = 0.0025 كجم/م والسلسلة 2 لها كثافة كتلة خطية تبلغ\(\mu_{2}\) = 0.0035 كجم/م. تتولد نبضات الموجة العرضية في وقت واحد في طرفي نقيض من السلاسل. كم من الوقت يمر قبل أن تمر النبضات بعضها البعض؟

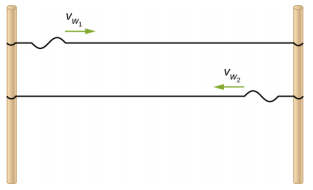
70. يتم ربط سلسلتين بين قطبين يفصل بينهما مسافة 2.00 متر كما هو موضح في الشكل السابق، وكلا السلاسل لها كثافة خطية تبلغ\(\mu_{1}\) = 0.0025 كجم/م، والتوتر في السلسلة 1 هو 600.00 نيوتن، والتوتر في السلسلة 2 هو 700.00 N. تتولد نبضات الموجة العرضية في وقت واحد عند الأطراف المقابلة للأوتار. كم من الوقت يمر قبل أن تمر النبضات بعضها البعض؟
71. يتم تشغيل النوتة E ₄ على البيانو وترددها f = 393.88. إذا كانت كثافة الكتلة الخطية لهذا الوتر من البيانو\(\mu\) = 0.012 kg/m وكان الوتر تحت الشد 1000.00 N، فما سرعة الموجة على الوتر والطول الموجي للموجة؟
72. تنتقل موجتان عرضيتان عبر خيط مشدود. سرعة كل موجة هي v = 30.00 m/s، ويوضح الرسم البياني للموضع الرأسي كدالة للموضع الأفقي أدناه للوقت t = 0.00 ثانية. (a) ما الطول الموجي لكل موجة؟ (ب) ما تردد كل موجة؟ (ج) ما هي السرعة الرأسية القصوى لكل سلسلة؟

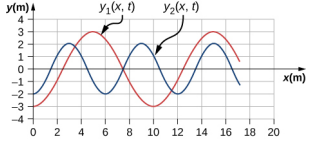
73. تنتقل موجة جيبية عبر خيط أفقي مشدود بكثافة كتلة خطية مقدارها = 0.060 كجم/م. أقصى سرعة رأسية للموجة هي vy max = 0.30 سم/ثانية، وقد تم تصميم الموجة باستخدام معادلة الموجة y (x, t) = A sin (6.00 m ⁻¹ x − 24.00 s ⁻¹ t). (أ) ما سعة الموجة؟ (ب) ما مقدار الشد في الخيط؟
74. سرعة الموجة العرضية على الخيط هي v = 60.00 م/ث والتوتر في السلسلة هو F _T = 100.00 N. ماذا يجب أن يكون مقدار الشد لزيادة سرعة الموجة إلى v = 120.00 m/s؟

16.4 طاقة الموجة وقوتها

75. خيط طوله ٥ م وكتلته ٩٠ جم مُثبَّت تحت شدٍّ مقداره ١٠٠ نيوتن. تنتقل موجة أسفل الوتر المُمثَّل بالشكل y (x، t) = 0.01 م\(\sin\) (15.7 م ⁻¹ x − 1170.12 ث ⁻¹). ما القدرة على طول موجة واحد؟
76. يتم إنتاج الموجات فوق الصوتية ذات الكثافة 1.50 × 10 ^{2 W/m 2} بواسطة الرأس المستطيل لجهاز التصوير الطبي بقياس 3.00 سم × 5.00 سم. ما هو خرج الطاقة الخاص بها؟
77. تبلغ مساحة مكبر الصوت منخفض التردد لمجموعة الاستريو A = 0.05 m ² وتنتج 1 واط من الطاقة الصوتية. (أ) ما هي الكثافة عند المتحدث؟ (ب) إذا كان مكبر الصوت يصدر صوتًا موحدًا في جميع الاتجاهات، فما المسافة من السماعة التي تبلغ شدتها 0.1 واط/م ²؟
78. لزيادة شدة الموجة بعامل ٥٠، ما العامل الذي ينبغي زيادة السعة به؟
79. يتم استخدام جهاز يسمى مقياس التشمس لقياس شدة ضوء الشمس. تبلغ مساحته 100 سم ² ويسجل 6.50 وات. ما الكثافة بوحدة W/m ²؟
80. تصل الطاقة من الشمس إلى قمة الغلاف الجوي للأرض بكثافة 1400 واط/م ². ما المدة التي يستغرقها 1.80 × 10 ⁹ J للوصول إلى مساحة 1.00 م ²؟
81. لنفترض أن لديك جهازًا يستخرج الطاقة من كاسحات المحيطات بما يتناسب بشكل مباشر مع شدتها. إذا كان الجهاز ينتج ١٠٫٠ كيلوواط من الطاقة في اليوم الذي يبلغ فيه ارتفاع القواطع ١٫٢٠ مترًا، فما مقدار الطاقة التي سينتج عنها عندما يبلغ ارتفاعها ٠٫٦٠٠ متر؟
82. تتميز مجموعة الخلايا الكهروضوئية من (الخلايا الشمسية) بكفاءة 10.0% في جمع الطاقة الشمسية وتحويلها إلى كهرباء. إذا كان متوسط شدة ضوء الشمس في يوم واحد ٧٠٫٠٠ ^{واط/متر} مربع، فما المساحة التي يجب أن تجمع فيها المصفوفة الطاقة بمعدل ١٠٠ واط؟ (ب) ما هي التكلفة القصوى للمصفوفة إذا كان عليها أن تدفع تكاليفها بنفسها في غضون عامين من التشغيل بمتوسط 10.0 ساعات في اليوم؟ افترض أنه يكسب المال بمعدل 9.00 سنتات لكل كيلوواط/ساعة.
83. يقوم الميكروفون الذي يستقبل نغمة صوت نقية بتغذية راسم الذبذبات، مما ينتج موجة على شاشته. إذا كانت شدة الصوت في الأصل 2.00 × 10 ⁻⁵ وات/م ²، ولكن تم رفعها حتى تزداد السعة بنسبة 30.0%، فما الكثافة الجديدة؟
84. طول خيط كتلته ٠٫٣٠ كجم يساوي ٤٫٠٠ م، وإذا كان الشد في الوتر يساوي ٥٠٫٠٠ نيوتن، وكانت موجة جيبية بسعة ٢٫٠٠ سم مستحثة على الوتر، فما التردد الذي يجب أن يكون لطاقة متوسطة مقدارها ١٠٠٫٠٠ واط؟
85. يوضح الشكل السابق القوة مقابل الوقت لنقطة على سلسلة (\(\mu\)= 0.05 كجم/م) يتم فيها إحداث موجة متحركة جيبية. تم تصميم الموجة باستخدام معادلة الموجة y (x، t) = A sin (20.93 m ⁻¹ x −\(\omega\) t). ما تردد واتساع الموجة؟
86. يوجد خيط تحت الضغط F _T1. تنتقل الطاقة عن طريق موجة على السلسلة بمعدل P ₁ بواسطة موجة تردد f ₁. ما نسبة معدل نقل الطاقة الجديد P ₂ إلى P ₁ إذا تضاعف التوتر؟
87. يتم ضرب شوكة رنانة بتردد 250 هرتز وتكون الكثافة عند المصدر I1 على مسافة متر واحد من المصدر. (أ) ما هي الكثافة على مسافة 4.00 أمتار من المصدر؟ (ب) ما مدى بُعد الشوكة الرنانة عن الشوكة الرنانة التي تساوي عُشر الكثافة عند المصدر؟ 88. تم تصنيف مكبر الصوت بجهد P = 120.00 فولت وتيار I = 10.00 A. استهلاك الطاقة الكهربائية هو P = IV. لاختبار السماعة، يتم تطبيق إشارة الموجة الجيبية على السماعة. بافتراض أن الموجة الصوتية تتحرك كموجة كروية وأن كل الطاقة المطبقة على السماعة قد تم تحويلها إلى طاقة صوتية، فما المسافة من السماعة التي تساوي الكثافة 3.82 W/m ²؟
88. تتناسب طاقة التموج على البركة مع مربع السعة. إذا كانت سعة التموج 0.1 سم على مسافة من المصدر مقدارها 6.00 أمتار، فما السعة على مسافة 2.00 متر من المصدر؟

16.5 تداخل الموجات

90. خذ بعين الاعتبار موجتين جيبيتين تتحركان على طول خيط، على غرار y ₁ (x، t) = 0.3 م sin (4 م ⁻¹ x + 3 s ⁻¹ t) و y ₂ (x، t) = 0.6 م sin (8 م ⁻¹ x − 6 ث ⁻¹ t). ما ارتفاع الموجة الناتجة الناتجة عن تداخل الموجتين عند الموضع x = 0.5 m في الوقت t = 0.2 ثانية؟
91. خذ بعين الاعتبار موجتين جيبيتين تسيران على طول خيط، على غرار y ₁ (x، t) = 0.3 م sin (4 م ⁻¹ x + 3 s ⁻¹ t +\(\frac{\pi}{3}\)) و y ₂ (x، t) = 0.6 م sin (8 م ⁻¹ x − 6 ث ⁻¹ t). ما ارتفاع الموجة الناتجة الناتجة عن تداخل الموجتين عند الموضع x = 1.0 m في الوقت t = 3.0 s؟
92. خذ بعين الاعتبار موجتين جيبيتين تسيران على طول خيط، على غرار y ₁ (x، t) = 0.3 م sin (4 م ⁻¹ x − 3 s ⁻¹ t) و y ₂ (x، t) = 0.3 م sin (4 م ⁻¹ x + 3 ث ⁻¹ t). ما الدالة الموجية للموجة الناتجة؟ [تلميح: استخدم علامة هوية المثلث (u ± v) = sin u cos v ± cos u sin v]
93. تتحرَّك موجتان جيبيتان في وسط في نفس الاتجاه، وتبلغ سعة كل منهما ٣٫٠٠ سم، وطول موجة ٥٫٢٠ م، وفترة ٦٫٥٢ ثانية، في حين تبلغ زاوية الإزاحة الطورية لأحدهما\(\phi\). ما مقدار التحول الطوري إذا كانت سعة الموجة الناتجة ٥٫٠٠ سم؟ [تلميح: استخدم تسجيل هوية المثلثات +sin v = 2 sin\(\left(\dfrac{u + v}{2}\right)\) cos\(\left(\dfrac{u − v}{2}\right)\)]
94. تتحرَّك موجتان جيبيتان في وسط في الاتجاه السيني الموجب، وتبلغ سعة كل منهما 6.00 سم، وطولها الموجي 4.3 م، وفترة 6.00 ثانية، ولكن إحداهما لها إزاحة طورية بزاوية\(\phi\) = 0.50 راد. ما ارتفاع الموجة الناتجة عند زمن t = 3.15 ثانية والموضع x = 0.45 m؟
95. تتحرَّك موجتان جيبيتان في وسط في الاتجاه السيني الموجب، وتبلغ سعة كل منهما 7.00 سم، ورقم الموجة k = 3.00 m−1، والتردد الزاوي\(\omega\) = 2.50 ثانية ⁻¹، وفترة 6.00 ثانية، ولكن لدى واحدة إزاحة طورية بزاوية\(\phi\) =\(\frac{\pi}{12}\) راد. ما ارتفاع الموجة الناتجة عند زمن t = 2.00 ثانية والموضع x = 0.53 m؟
96. ضع في اعتبارك موجتين y ₁ (x، t) و y ₂ (x، t) متطابقتان باستثناء التحول الطوري الذي ينتشر في نفس الوسيط. (أ) ما مقدار التغيُّر الطوري، بالراديان، إذا كانت سعة الموجة الناتجة تساوي 1.75 ضعف سعة الموجات الفردية؟ (ب) ما هو التحول المرحلي في الدرجات؟ (ج) ما هو التحول الطوري كنسبة مئوية من الطول الموجي الفردي؟
97. تسير موجتان جيبيتان متماثلتان باستثناء التحول الطوري في نفس الاتجاه. المعادلة الموجية للموجة الناتجة هي y _R (x, t) = 0.70 م sin (3.00 م ⁻¹ x − 6.28 s ⁻¹ t +\(\frac{\pi}{16}\) rad). ما التردد الزاوي وعدد الموجات والسعة والتحول الطوري للموجات الفردية؟
98. تسير موجتان جيبيتان متماثلتان باستثناء التحول الطوري في نفس الاتجاه. المعادلة الموجية للموجة الناتجة هي y _R (x, t) = 0.35 سم خطيئة (6.28 م ⁻¹ x − 1.57 s ⁻¹ t +\(\frac{\pi}{4}\)). ما الفترة والطول الموجي والسعة والتحول الطوري للموجات الفردية؟
99. ضع في اعتبارك وظيفتين للموجة، y ₁ (x، t) = 4.00 م sin (\(\pi\)m ⁻¹ x −\(\pi\) s ⁻¹ t) و y ₂ (x، t) = 4.00 م sin (\(\pi\)m ⁻¹ x −\(\pi\) s ⁻¹ t +\(\frac{\pi}{3}\)). (أ) باستخدام جدول بيانات، ارسم وظيفتي الموجة والموجة الناتجة عن تراكب داليتي الموجة كدالة للموضع (0.00 ≤ x ≤ 6.00 m) للوقت t = 0.00 ثانية. (ب) ما الطول الموجي والسعة للموجتين الأصليتين؟ (ج) ما الطول الموجي والسعة للموجة الناتجة؟
100. ضع في اعتبارك وظيفتين للموجة، y ₂ (x، t) = 2.00 م خطيئة (\(\frac{\pi}{2}\)m ⁻¹ x −\(\frac{\pi}{3}\) s ⁻¹ t) و y ₂ (x، t) = 2.00 م خطيئة (\(\frac{\pi}{2}\)م ⁻¹ x −\(\frac{\pi}{3}\) s ⁻¹ t +\(\frac{\pi}{6}\)). (أ) تحقق من أن y _R = 2A cos\(\left(\dfrac{\phi}{2}\right)\) sin (kx −\(\omega\) t +\(\frac{\phi}{2}\)) هو الحل للموجة التي تنتج عن تراكب الموجتين. اصنع عمودًا لـ x و y ₁ و y ₂ و y ₁ + y ₂ و y _R = 2A cos\(\left(\dfrac{\phi}{2}\right)\) sin (kx −\(\omega\) t +\(\frac{\phi}{2}\)). ارسم أربع موجات كدالة للموضع حيث يتراوح نطاق x من 0 إلى 12 مترًا.
101. ضع في اعتبارك وظيفتين موجيتين تختلفان فقط عن طريق التحول الطوري، y ₁ (x، t) = A cos (kx −\(\omega\) t) و y ₂ (x، t) = A cos (kx −\(\omega\) t +\(\phi\)). استخدم الهويات المثلثية cos u + cos v = 2\(\left(\dfrac{u − v}{2}\right)\) cos cos\(\left(\dfrac{u + v}{2}\right)\) و cos (−\(\theta\)\(\theta\)) = cos () لإيجاد معادلة الموجة للموجة الناتجة عن تراكب الموجتين. هل تأتي وظيفة الموجة الناتجة كمفاجأة لك؟

16.6 الموجات الدائمة والرنين

102. تستغرق الموجة التي تنتقل على سيارة Slinky® الممتدة إلى 4 أمتار 2.4 ثانية للسفر على طول Slinky والعودة مرة أخرى. (أ) ما هي سرعة الموجة؟ (ب) باستخدام نفس السلينكي الممتد بنفس الطول، يتم إنشاء موجة دائمة تتكون من ثلاثة مضادات للأورام وأربع عقد. في أي تردد يجب أن تتأرجح سلينكي؟
103. خيط طوله ٢ متر ممتد بين دعامتين بشد ينتج عنه سرعة موجة تساوي v _w = ٥٠٫٠٠ م/ث، ما الطول الموجي والتردد للأنماط الثلاثة الأولى التي يتردد صداها على الوتر؟
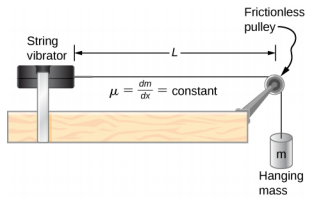
104. ضع في اعتبارك الإعداد التجريبي الموضح أدناه. طول الخيط بين الهزاز الخيطي والبكرة هو L = 1.00 m، والكثافة الخطية للخيط\(\mu\) = 0.006 kg/m، ويمكن أن يتذبذب الهزاز الخيطي بأي تردد. الكتلة المعلقة هي 2.00 كجم. (أ) ما الطول الموجي والتردد لوضع n = 6؟ (ب) تتأرجح السلسلة الهواء حول الخيط. ما الطول الموجي للصوت إذا كانت سرعة الصوت v _s = 343.00 m/s؟

105. يتم تعليق كبل بكثافة خطية تبلغ\(\mu\) = 0.2 كجم/م من أعمدة الهاتف. يبلغ التوتر في الكبل 500.00 نيوتن، والمسافة بين القطبين 20 مترًا. تهب الرياح عبر الخط، مما يتسبب في رنين الكابل. يتم إنتاج نمط الموجات الدائمة الذي يحتوي على 4.5 أطوال موجية بين القطبين. تبلغ سرعة الصوت عند درجة الحرارة الحالية T = 20° C 343.00 m/s. ما تردُّد الطنين وطوله الموجي؟
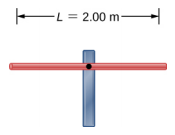
106. ضع في اعتبارك قضيبًا بطول L، مثبتًا في المنتصف على دعامة. يجب أن توجد عقدة حيث يتم تثبيت القضيب على دعامة، كما هو موضح أدناه. ارسم أول وضعين عاديين للقضيب أثناء دفعه إلى الرنين. قم بتسمية الطول الموجي والتردد المطلوب لدفع القضيب إلى الرنين.

107. ضع في اعتبارك وظيفتين للموجة y (x، t) = 0.30 سم خطيئة (3 م ⁻¹ × − 4 ث ⁻¹ t) و y (x، t) = 0.30 سم خطيئة (3 م ⁻¹ x + 4 ث ⁻¹ t). اكتب دالة الموجة للموجة الواقفة الناتجة.
108. يبلغ وزن سلك طوله 2.40 مترًا 7.50 جم ويقع تحت ضغط 160 نيوتن، ويتم تثبيت السلك بشكل صلب عند كلا الطرفين ويتم تثبيته في حالة تذبذب. (أ) ما سرعة الموجات على السلك؟ يُدفع الوتر إلى الرنين بواسطة تردد ينتج موجة واقفة بطول موجة يساوي 1.20 م. (ب) ما التردد المستخدم لدفع الوتر إلى الرنين؟
109. تم ضبط خيط بكثافة كتلته الخطية 0.0062 كجم/م وطوله 3.00 م في وضع الرنين n = 100. مقدار الشد في الخيط يساوي ٢٠٫٠٠ نيوتن. ما طول موجة الموجة وترددها؟
110. تم ضبط خيط بكثافة كتلته الخطية 0.0075 كجم/م وطوله 6.00 م في وضع الرنين n = 4 عن طريق القيادة بتردد 100.00 هرتز. ما مقدار الشد في الخيط؟
111. تنتقل موجتان جيبيتان لهما أطوال موجية واتساعات متطابقة في اتجاهين متعاكسين على طول خيط ينتج موجة دائمة. كثافة الكتلة الخطية للخيط\(\mu\) = 0.075 كجم/م والشد في الخيط هو F _T = 5.00 N. والفاصل الزمني بين حالات التداخل التدميري الكلي هو\(\Delta\) t = 0.13 ثانية، ما الطول الموجي للموجات؟
112. خيط مثبت على كلا الطرفين طوله ٥٫٠٠ م وكتلته ٠٫١٥ كجم. الشد إذا كان الوتر يساوي 90 نيوتن. يهتز الخيط لإنتاج موجة ثابتة عند التردد الأساسي للخيط. (أ) ما سرعة الموجات على الوتر؟ (ب) ما الطول الموجي للموجة الراكدة المنتجة؟ (ج) ما هي فترة الموجة الدائمة؟
113. تم إصلاح السلسلة في كلا الطرفين. تبلغ كتلة الخيط 0.0090 كجم وطوله 3.00 م، ويقع الوتر تحت شد قدره 200.00 نيوتن، ويتم تحريك الخيط بواسطة مصدر تردد متغير لإنتاج موجات ثابتة على الوتر. أوجد الأطوال الموجية والتردد للأنماط الأربعة الأولى للموجات الراكدة.
114. ترددات نمطين متتاليين من الموجات الواقفة على السلسلة هي 258.36 هرتز و 301.42 هرتز. ما التردد التالي فوق 100.00 هرتز الذي ينتج موجة دائمة؟
115. خيط مثبت في كلا الطرفين لدعم يفصل بينهما مسافة ٣٫٥٠ مترًا، وكثافته الكتلية الخطية\(\mu\) = 0.005 كجم/م، ويقع الوتر تحت شد قدره ٩٠٫٠٠ نيوتن، وتُنتَج موجة ثابتة على الوتر ذي ست عُقد وخمسة مضادات. ما سرعة الموجة والطول الموجي والتردد وفترة الموجة الواقفة؟
116. يتم إرسال الموجات الجيبية عبر خيط بطول 1.5 متر مثبت في كلا الطرفين. تنعكس الموجات مرة أخرى في الاتجاه المعاكس. سعة الموجة هي 4.00 سم. تبلغ سرعة انتشار الموجات 175 متر/ثانية، ويتم إنتاج وضع الرنين n = 6 للخيط. اكتب معادلة للموجة الواقفة الناتجة.

مشاكل إضافية

117. تستخدم معدات الموجات فوق الصوتية المستخدمة في مهنة الطب موجات صوتية بتردد أعلى من نطاق السمع البشري. إذا كان تردد الصوت الصادر عن جهاز الموجات فوق الصوتية f = 30 كيلوهرتز، فما الطول الموجي للموجات فوق الصوتية في العظم، إذا كانت سرعة الصوت في العظم v = 3000 m/s؟
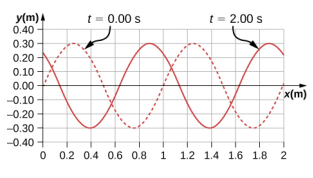
118. يظهر أدناه مخطط دالة الموجة التي تمثل الموجة في الوقت t = 0.00 ثانية و t = 2.00 ثانية. الخط المنقط هو دالة الموجة في الوقت t = 0.00 ثانية والخط الصلب هو الدالة في الوقت t = 2.00 ثانية. قم بتقدير سعة الموجة وطولها الموجي وسرعتها وفترتها.

119. تبلغ سرعة الضوء في الهواء حوالي v = 3.00 x 10 ⁸ m/s وسرعة الضوء في الزجاج v = 2.00 x 10 ⁸ m/s، ويضيء ليزر أحمر بطول موجة\(\lambda\) = 633.00 nm الضوء الساقط من الزجاج، وينتقل بعض الضوء الأحمر إلى الزجاج. تردد الضوء هو نفسه بالنسبة للهواء والزجاج. (أ) ما هو تردد الضوء؟ (ب) ما الطول الموجي للضوء في الزجاج؟
120. تبث محطة إذاعية موجات راديو بتردد 101.7 ميجاهرتز. تتحرك موجات الراديو عبر الهواء بسرعة الضوء تقريبًا في الفراغ. ما الطول الموجي للموجات الراديوية؟
121. يقف حمام شمسي في عمق الخصر في المحيط ويلاحظ أن ست قمم من الموجات السطحية الدورية تمر كل دقيقة. تقع القمم على بعد 16.00 متر. ما الطول الموجي والتردد والفترة والسرعة للموجات؟
122. تهتز شوكة رنانة وتنتج صوتًا بتردد 512 هرتز. تبلغ سرعة الصوت في الهواء v = 343.00 m/s إذا كان الهواء عند درجة حرارة 20.00 °س، فما الطول الموجي للصوت؟
123. يتحرك زورق آلي عبر بحيرة بسرعة v _b = 15.00 m/s، ويرتد القارب لأعلى ولأسفل كل 0.50 ثانية أثناء تحركه في نفس اتجاه الموجة. وهي ترتد صعودًا وهبوطًا كل 0.30 ثانية أثناء انتقالها في اتجاه معاكسٍ لاتجاه الموجات. ما سرعة الموجة وطولها الموجي؟
124. استخدم معادلة الموجة الخطية لتوضيح أن السرعة الموجية لموجة مصممة باستخدام دالة الموجة y (x, t) = 0.20 م sin (3.00 m ⁻¹ x + 6.00 s ⁻¹ t) هي v = 2.00 m/s. ما الطول الموجي وسرعة الموجة؟
125. بالنظر إلى وظائف الموجة y ₁ (x، t) = A sin (kx −\(\omega\) t) و y ₂ (x، t) = A sin (kx −\(\omega\) t +\(\phi\)) مع\(\phi \neq \frac{\pi}{2}\)، أظهر أن y ₁ (x، t) + y ₂ (x، t) هو حل لمعادلة الموجة الخطية بسرعة موجة قدرها v =\(\frac{\omega}{k}\).
126. تم تصميم موجة عرضية على سلسلة باستخدام دالة الموجة y (x، t) = 0.10 م sin (0.15 م ⁻¹ x + 1.50 ثانية ⁻¹ t + 0.20). (أ) أوجد سرعة الموجة. (ب) أوجد الموضع في الاتجاه y، والسرعة العمودية على حركة الموجة، والتسارع العمودي على حركة الموجة، لجزء صغير من الخيط المتمركز عند x = 0.40 m في الوقت t = 5.00 ثانية.
127. تنتقل الموجة الجيبية إلى أسفل خيط أفقي مشدود بكثافة كتلتها الخطية\(\mu\) = 0.060 كجم/م، ويكون مقدار التسارع الرأسي الأقصى للموجة ay max = 0.90 سم/ثانية ² وسعة الموجة 0.40 m، ويقع الوتر تحت توتر F _T = 600.00 N. تتحرك الموجة في الاتجاه السيني السلبي. اكتب معادلة لتمثيل الموجة.
128. يتم وصف الموجة العرضية على سلسلة (\(\mu\)= 0.0030 كجم/م) بالمعادلة y (x، t) = 0.30 m sin\(\left(\dfrac{2 \pi}{4.00\; m}(x − 16.00\; m/s\; t)\right)\). ما مقدار الشد الذي يتم تثبيت الخيط تحته بشكل مشدود؟
129. يتم وصف الموجة العرضية على سلسلة أفقية (\(\mu\)= 0.0060 كجم/م) بالمعادلة y (x، t) = 0.30 m sin\(\left(\dfrac{2 \pi}{4.00\; m(x − v_{w}t)}\right)\). يقع الوتر تحت شد قدره 300.00 نيوتن. ما سرعة الموجة ورقم الموجة والتردد الزاوي للموجة؟
130. يحمل الطالب مكتشف النطاق الصوتي غير المكلف ويستخدم أداة البحث عن المدى للعثور على المسافة إلى الحائط. يصدر مكتشف النطاق الصوتي موجة صوتية. تنعكس الموجة الصوتية عن الحائط وتعود إلى أداة البحث عن النطاق. تستغرق الرحلة ذهابًا وإيابًا 0.012 ثانية، وقد تمت معايرة أداة تحديد النطاق للاستخدام في درجة حرارة الغرفة T = 20 درجة مئوية، ولكن درجة الحرارة في الغرفة هي في الواقع T = 23 درجة مئوية، وبافتراض أن آلية التوقيت مثالية، ما نسبة الخطأ التي يمكن أن يتوقعها الطالب بسبب المعايرة؟
131. تُحرَّك الموجة الموجودة على الوتر بواسطة هزاز خيطي يتذبذب بتردد 100.00 هرتز وسعة مقدارها ١٫٠٠ سم. يعمل الهزاز الوتري بجهد 12.00 فولت وتيار 0.20 أمبير. الطاقة التي يستهلكها الهزاز الخيطي هي P = IV. افترض أن الهزاز الوتري فعال بنسبة 90٪ في تحويل الطاقة الكهربائية إلى طاقة مرتبطة باهتزازات السلسلة. طول الخيط ٣٫٠٠ م، ويقع تحت الشد ٦٠٫٠٠ نيوتن. ما كثافة الكتلة الخطية للخيط؟
132. تُمثَّل الموجة المتحركة على الوتر بالمعادلة الموجية y (x, t) = 3.00 سم خطيئة (8.00 م ⁻¹ x + 100.00 s ⁻¹ t). يقع الخيط تحت شدٍّ مقداره 50.00 نيوتن وكثافته الكتلية الخطية\(\mu\) = 0.008 كجم/م، ما متوسط القدرة التي تنقلها الموجة على الوتر؟
133. طول موجة عرضية على خيط طوله الموجي ٥٫٠ م، ومدتها ٠٫٠٢ ثانية، وسعة مقدارها ١٫٥ سم. متوسط القدرة التي تنقلها الموجة هو 5.00 W. ما مقدار الشد في الخيط؟
134. (أ) ما شدة شعاع الليزر المستخدم لحرق الأنسجة السرطانية التي تضع 500 جول من الطاقة في بقعة دائرية قطرها 2.00 مم في 4.00 ثانية عند امتصاصها بنسبة 90 في المائة؟ (ب) ناقش كيفية مقارنة هذه الكثافة بمتوسط شدة ضوء الشمس (حوالي) والآثار المترتبة على ذلك إذا دخل شعاع الليزر عينك. لاحظ كيف تعتمد إجابتك على المدة الزمنية للتعرض.
135. ضع في اعتبارك وظيفتين للموجة الدورية، y ₁ (x، t) = A sin (kx −\(\omega\) t) و y ₂ (x، t) = A sin (kx −\(\omega\) t +\(\phi\)). (أ) ما هي\(\phi\) قيم الموجة الناتجة عن تراكب دوال الموجة التي تبلغ سعتها 2A؟ (ب) ما هي قيم الموجة الناتجة عن تراكب دوال الموجة بسعة صفر؟\(\phi\)
136. ضع في اعتبارك وظيفتين للموجة الدورية، y ₁ (x، t) = A sin (kx −\(\omega\) t) و y ₂ (x، t) = A cos (kx −\(\omega\) t +\(\phi\)). (أ) ما هي\(\phi\) قيم الموجة الناتجة عن تراكب دوال الموجة التي تبلغ سعتها 2A؟ (ب) ما هي قيم الموجة الناتجة عن تراكب دوال الموجة بسعة صفر؟\(\phi\)
137. حوض صغير بأبعاد 10.00 متر × 0.10 متر × 0.10 متر مملوء جزئيًا بالماء. يتم إنتاج موجات المياه السطحية ذات السعة الصغيرة من كلا طرفي الحوض بواسطة المجاذيف التي تتأرجح بحركة توافقية بسيطة. تم تصميم ارتفاع موجات الماء بمعادلتين للموجات الجيبية، y ₁ (x، t) = 0.3 م sin (4 م ⁻¹ x − 3 s ⁻¹ t) و y ₂ (x، t) = 0.3 م كوس (4 م ⁻¹ x + 3 ث ⁻¹ t -\(\frac{\pi}{2}\)). ما وظيفة الموجة للموجة الناتجة بعد وصول الموجات إلى بعضها البعض وقبل أن تصل إلى نهاية الحوض الصغير (بمعنى، افترض وجود موجتين فقط في الحوض الصغير وتجاهل الانعكاسات)؟ استخدم جدول بيانات للتحقق من نتائجك. [تلميح: استخدم هويات المثلثات sin (u ± v) = sin u cos v ± cos u sin v و cos (u ± v) = cos u cos v sin u sin v]
138. يسجل جهاز قياس الزلازل موجات S و P من زلزال يبعد مسافة 20.00 ثانية. إذا ساروا في نفس المسار بسرعات موجية ثابتة تبلغ v _S = 4.00 كم/ثانية و v _P = 7.50 كم/ثانية، فما مدى بُعد مركز الزلزال؟
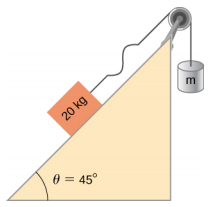
139. ضع في اعتبارك ما هو موضح أدناه. ترتكز كتلة وزنها 20.00 كجم على منحدر غير احتكاكي يميل بزاوية 45°. خيط بكثافة كتلته الخطية\(\mu\) = 0.025 كجم/م موصولة بكتلة 20.00 kg. يمر الخيط فوق بكرة غير قابلة للاحتكاك ذات كتلة ضئيلة ويتم توصيله بكتلة معلقة (m). النظام في حالة توازن ثابت. يتم إحداث موجة على الخيط وتنتقل إلى أعلى المنحدر. (أ) ما كتلة الكتلة المعلقة (م)؟ (ب) ما سرعة الموجة التي تنتقل بها الموجة إلى أعلى الوتر؟

140. ضع في اعتبارك تراكب ثلاث وظائف موجية y (x، t) = 3.00 سم sin (2 م ⁻¹ x − 3 ث ⁻¹ t)، y (x، t) = 3.00 سم الخطيئة (6 م ⁻¹ x + 3 ث ⁻¹ t)، و y (x، t) = 3.00 سم الخطيئة (2 م ⁻¹ x − 4 ث ⁻¹ t). ما ارتفاع الموجة الناتجة عند الموضع x = 3.00 m في الوقت t = 10.0 ثانية؟
141. خيط كتلته ١٥٠ جم وطوله ٣٫٤ م، ويُثبَت أحد طرفيه على حامل مختبر، بينما يُربط الطرف الآخر بنابض ثابت زنبركي يساوي k _s = ١٠٠ نيوتن/م، ويُربط الطرف الحر للزنبرك بعمود مختبر آخر. يتم الحفاظ على التوتر في السلسلة بواسطة الزنبرك. يتم فصل أقطاب المختبر بمسافة تمتد على الزنبرك بمقدار 2.00 سم. يتم سحب الخيط وتنتقل النبضة على طول الخيط. ما سرعة انتشار النبضة؟
142. تُنتَج الموجة الواقفة على خيط يقع تحت توتر مقداره ٧٠٫٠ نيوتن بواسطة موجتين عرضيتين جيبيتين متماثلتين، ولكن تتحركان في اتجاهين متعاكسين. تم تثبيت الخيط عند x = 0.00 م و x = 10.00 م، وتظهر العقد عند x = 0.00 م و 2.00 م و 4.00 م و 6.00 م و 8.00 م و 10.00 م، وتبلغ سعة الموجة الواقفة 3.00 سم. يستغرق الأمر 0.10 ثانية حتى تقوم مضادات الإينودات بعمل تذبذب كامل واحد. (أ) ما هي الدوال الموجية للموجتين الجيبيتين اللتين تنتجان الموجة الراكدة؟ (ب) ما هي السرعة القصوى والتسارع القصوى للخيط، عموديًا على اتجاه حركة الموجات العرضية، عند الأجسام المضادة؟
143. يتم تثبيت خيط بطول 4 أمتار تحت توتر مستمر. تبلغ كثافة الكتلة الخطية للخيط\(\mu\) = 0.006 كجم/م، وترددان الرنين للخيط هما 400 هرتز و 480 هرتز. لا توجد ترددات رنين بين الترددين. (أ) ما هي الأطوال الموجية لوضعي الرنين؟ (ب) ما مقدار الشد في الخيط؟

مشاكل التحدي

144. سلك نحاسي نصف قطر ٢٠٠\(\mu\) متر وطوله ٥٫٠ م، ويوضع السلك تحت شدٍّ مقداره ٣٠٠٠ نيوتن، ويمتد السلك بمقدار صغير. يتم سحب السلك وتنتقل النبضة عبر السلك. ما سرعة انتشار النبضة؟ (افترض أن درجة الحرارة لا تتغير: (\(\rho\)= 8.96 جم/سم ³، Y = 1.1 × 10 ¹¹ نيوتن/م).
145. يمكن تصميم نبضة تتحرك على طول المحور x كدالة الموجة y (x، t) = 4.00 m\(e^{− \left(\dfrac{x + (2.00\; m/s)t}{1.00\; m}\right)^{2}}\). (أ) ما اتجاه النبض وسرعة انتشاره؟ (ب) إلى أي مدى تحركت الموجة خلال 3.00 ثانية؟ (ج) رسم النبض باستخدام جدول بيانات في الوقت t = 0.00 ثانية و t = 3.00 ثانية للتحقق من إجابتك في الجزء (ب).
146. تم تثبيت خيط بكثافة كتلته الخطية\(\mu\) = 0.0085 كجم/م عند كلا الطرفين. تم تعليق كتلة مقدارها 5.0 كجم من الخيط، كما هو موضح أدناه. إذا أُرسلت نبضة على طول القسم A، فما سرعة الموجة في القسم A وسرعة الموجة في القسم B؟

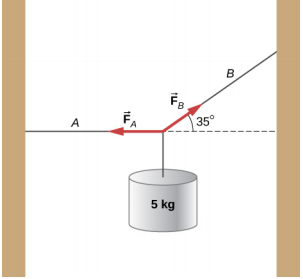
147. ضع في اعتبارك وظيفتين للموجة y ₁ (x، t) = A sin (kx −\(\omega\) t) و y ₂ (x، t) = A sin (kx +\(\omega\) t +\(\phi\)). ما دالة الموجة الناتجة عن تداخل الموجتين؟ [تلميح: sin (\(\alpha \pm \beta\)) = sin\(\alpha\) cos\(\beta\) ± cos\(\alpha\) sin\(\beta\) and\(\phi = \frac{\phi}{2} + \frac{\phi}{2}\)).
148. تُعطى الدالة الموجية التي تُمثِّل الموجة الواقفة على النحو yR (x, t) = 6.00 سم خطيئة (3.00 م ⁻¹ x + 1.20 راد) cos (6.00 ثانية ⁻¹ t + 1.20 راد). ما الدالتان الموجيتان اللتان تتداخلان لتكوين دالة الموجة هذه؟ ارسم وظيفتي الموجة ومجموع دالتي الموجة عند t = 1.00 s للتحقق من إجابتك.
149. ضع في اعتبارك وظيفتين للموجة y ₁ (x، t) = A sin (kx −\(\omega\) t) و y ₂ (x، t) = A sin (kx +\(\omega\) t +\(\phi\)). شكل الموجة الناتج عند إضافة الوظيفتين هو y _R = 2A sin (kx +\(\frac{\phi}{2}\)) cos (\ omega t +\ frac {\ phi} {2}\)). ضع في اعتبارك الحالة التي تكون فيها A = 0.03 م ⁻¹، k = 1.26 م ⁻¹،\(\omega = \pi\) s ⁻¹، و\(\phi = \frac{\pi}{10}\). (أ) أين تبدأ العقد الثلاث الأولى من دالة الموجة الواقفة من الصفر وتتحرك في اتجاه x الموجب؟ (ب) باستخدام جدول بيانات، ارسم وظيفتي الموجة والوظيفة الناتجة في الوقت t = 1.00 ثانية للتحقق من إجابتك.