16.7: الموجات الدائمة والرنين
- Page ID
- 199843
- وصف الموجات الواقفة وشرح كيفية إنتاجها
- وصف أنماط الموجة الواقفة على سلسلة
- قدِّم أمثلة للموجات الواقفة خارج الموجات الموجودة على الخيط
خلال هذا الفصل، كنا ندرس الموجات المتحركة، أو الموجات التي تنقل الطاقة من مكان إلى آخر. في ظل ظروف معينة، يمكن أن ترتد الأمواج ذهابًا وإيابًا عبر منطقة معينة، وتصبح ثابتة بشكل فعال. تسمى هذه الموجات الواقفة.
تأثير آخر ذو صلة يعرف باسم الرنين. في التذبذبات، قمنا بتعريف الرنين كظاهرة يمكن فيها لقوة دافعة ذات سعة صغيرة أن تنتج حركة ذات سعة كبيرة. فكر في طفل على الأرجوحة، والتي يمكن تصميمها على شكل بندول مادي. يمكن أن تؤدي عمليات الدفع ذات السعة الصغيرة نسبيًا من قبل أحد الوالدين إلى تقلبات كبيرة في السعة. في بعض الأحيان يكون هذا الرنين جيدًا - على سبيل المثال، عند إنتاج الموسيقى باستخدام آلة وترية. في أوقات أخرى، يمكن أن تكون الآثار مدمرة، مثل انهيار مبنى أثناء الزلزال. في حالة الموجات الراكدة، يتم إنتاج الموجات الدائمة ذات السعة الكبيرة نسبيًا عن طريق تراكب موجات مكونات السعة الأصغر.
موجات دائمة
في بعض الأحيان لا يبدو أن الموجات تتحرك؛ بل إنها تهتز فقط في مكانها. يمكنك رؤية موجات غير متحركة على سطح كوب من الحليب في الثلاجة، على سبيل المثال. تخلق الاهتزازات من محرك الثلاجة موجات على الحليب تتأرجح لأعلى ولأسفل ولكن لا يبدو أنها تتحرك عبر السطح. \(\PageIndex{1}\)يوضح الشكل تجربة يمكنك تجربتها في المنزل. خذ وعاءًا من الحليب وضعه على مروحة صندوقية مشتركة. تنتج الاهتزازات الصادرة من المروحة موجات دائمة دائرية في الحليب. تظهر الموجات في الصورة بسبب الانعكاس من المصباح. تتكون هذه الموجات من خلال تراكب موجتين متحركتين أو أكثر، كما هو موضح في الشكل\(\PageIndex{2}\) لموجتين متطابقتين تتحركان في اتجاهين متعاكسين. تتحرك الأمواج عبر بعضها البعض مع زيادة اضطراباتها مع مرورها. إذا كانت الموجتان لهما نفس السعة والطول الموجي، فإنهما يتناوبان بين التداخل البنائي والمدمر. تبدو النتيجة وكأنها موجة واقفة في مكانها، وبالتالي تسمى الموجة الدائمة.

فكر في موجتين متطابقتين تتحركان في اتجاهين متعاكسين. للموجة الأولى دالة موجة y 1 (x، t) = A sin (kx −\(\omega\) t) والموجة الثانية لها دالة الموجة y 2 (x، t) = A sin (kx +\(\omega\) t). تتداخل الموجات وتشكل موجة ناتجة.
\[\begin{split} y(x,t) & = y_{1} (x,t) + y_{2} (x,t), \\ & = A \sin (kx - \omega t) + A \sin (kx + \omega t) \ldotp \end{split}\]
يمكن تبسيط ذلك باستخدام الهوية المثلثية
\[\sin (\alpha \pm \beta) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta,\]
أين\(\alpha\) = kx و\(\beta\) =\(\omega\) t، مما يعطينا
\[y(x,t) = A[\sin (kx) \cos (\omega t) - \cos (kx) \sin (\omega t) + \sin (kx) \cos (\omega t) - \cos (kx) \sin (\omega t)],\]
الذي يبسط إلى
\[y(x,t) = 2A \sin (kx) \cos (\omega t) \ldotp \label{16.14}\]
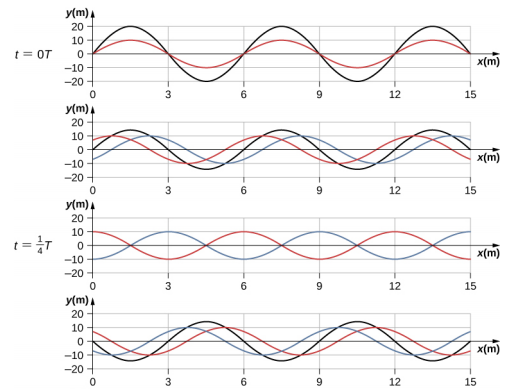
لاحظ أن الموجة الناتجة هي موجة جيبية دالة للموضع فقط، مضروبة في دالة جيب التمام التي تمثل دالة الوقت فقط. تظهر الرسوم البيانية لـ y (x، t) كدالة لـ x لأوقات مختلفة في الشكل\(\PageIndex{6}\). تتحرك الموجة الحمراء في الاتجاه السيني السلبي، وتتحرك الموجة الزرقاء في اتجاه x الإيجابي، والموجة السوداء هي مجموع الموجتين. عندما تتحرك الموجات الحمراء والزرقاء عبر بعضها البعض، فإنها تتحرك داخل وخارج التداخل البناء والتداخل المدمر.
في البداية، في الوقت t = 0، تكون الموجتان في الطور، والنتيجة هي موجة تبلغ ضعف سعة الموجات الفردية. تكون الموجات أيضًا في طور الطور في الوقت t =\(\frac{T}{2}\). في الواقع، تكون الموجات في طور أي عدد صحيح مضاعف لنصف الفترة:
t = n\(\frac{T}{2}\) حيث n = 0، 1، 2، 3... (في المرحلة).
في أوقات أخرى، تكون الموجتان 180 درجة (\(\pi\)راديان) خارج الطور، والموجة الناتجة تساوي صفرًا. يحدث هذا في
t =\(\frac{1}{4}\) T،\(\frac{3}{4}\) T،\(\frac{5}{4}\) T،...،\(\frac{n}{4}\) T حيث n = 1، 3، 5... (خارج المرحلة).
لاحظ أن بعض المواضع x للموجة الناتجة تكون دائمًا صفرية بغض النظر عن علاقة الطور. تسمى هذه المواضع العقد. أين تحدث العقد؟ ضع في اعتبارك الحل لمجموع الموجتين
\[y(x,t) = 2A \sin (kx) \cos (\omega t) \ldotp\]
يوفر العثور على المواضع التي تساوي فيها دالة الجيب صفرًا مواضع العقد.
\[\begin{split} \sin (kx) & = 0 \\ kx & = 0, \pi, 2 \pi, 3 \pi, \ldots \\ \frac{2 \pi}{\lambda} x & = 0, \pi, 2 \pi, 3 \pi, \ldots \\ x & = 0, \frac{\lambda}{2}, \lambda, \frac{3 \lambda}{2}, \ldots = n \frac{\lambda}{2} \quad n = 0, 1, 2, 3, \ldots \end{split}\]
هناك أيضًا مواضع تتأرجح فيها y بين y = ± A. هذه هي مضادات الالتهاب. يمكننا العثور عليها من خلال النظر في قيم النتيجة x في sin (kx) = ± 1.
\[\begin{split} \sin (kx) & = \pm 1 \\ kx & = \frac{\pi}{2}, \frac{3 \pi}{2}, \frac{5 \pi}{2}, \ldots \\ \frac{2 \pi}{\lambda} x & = \frac{\pi}{2}, \frac{3 \pi}{2}, \frac{5 \pi}{2}, \ldots \\ x & = \frac{\lambda}{4}, \frac{3 \lambda}{4}, \frac{5 \lambda}{4}, \ldots = n \frac{\lambda}{4} \quad n = 1, 3, 5, \ldots \end{split}\]
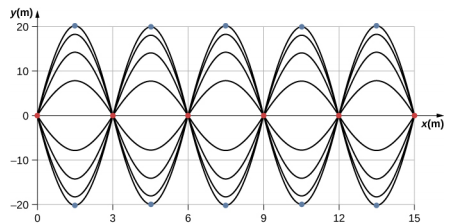
والنتيجة هي موجة واقفة كما هو موضح في الشكل\(\PageIndex{3}\)، والتي تعرض لقطات للموجة الناتجة من موجتين متطابقتين تتحركان في اتجاهين متعاكسين. يبدو أن الموجة الناتجة هي موجة جيبية ذات عقد عند مضاعفات عددية لنصف الأطوال الموجية. تتأرجح مضادات الأكسدة بين y = ± 2A بسبب مصطلح جيب التمام، cos (\(\omega\)t)، الذي يتأرجح بين ± 1.
يبدو أن الموجة الناتجة لا تزال قائمة، مع عدم وجود حركة واضحة في الاتجاه x، على الرغم من أنها تتكون من دالة موجة واحدة تتحرك في الموجب، بينما تتحرك الموجة الثانية في الاتجاه السيني السلبي. \(\PageIndex{3}\)يعرض الشكل لقطات مختلفة للموجة الناتجة. يتم تمييز العقد بنقاط حمراء بينما يتم تمييز مضادات الإينودات بنقاط زرقاء.
ومن الأمثلة الشائعة على الموجات الواقفة الموجات التي تنتجها الآلات الموسيقية الوترية. عندما يتم سحب الخيط، تنتقل النبضات على طول الخيط في اتجاهين متعاكسين. يتم تثبيت أطراف السلاسل في مكانها، بحيث تظهر العقد في نهايات السلاسل - الشروط الحدودية للنظام، التي تنظم ترددات الرنين في الأوتار. يمكن تصميم الرنين الناتج على آلة وترية في مختبر الفيزياء باستخدام الجهاز الموضح في الشكل\(\PageIndex{4}\).
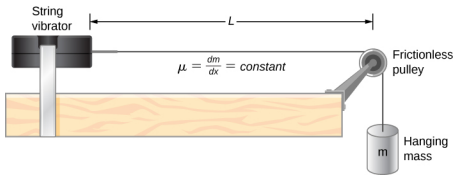
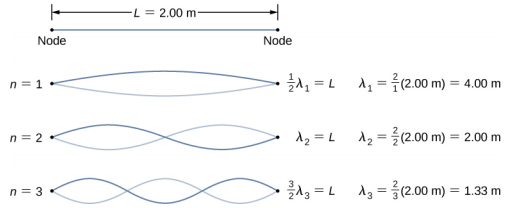
يُظهر الإعداد المعملي خيطًا موصولًا بهزاز خيطي، مما يؤدي إلى تذبذب الخيط بتردد قابل للتعديل f. ويمر الطرف الآخر من الخيط فوق بكرة خالية من الاحتكاك ومربوطًا بكتلة معلقة. حجم التوتر في السلسلة يساوي وزن الكتلة المعلقة. تحتوي السلسلة على كثافة خطية ثابتة (الكتلة لكل طول)\(\mu\) والسرعة التي تنتقل بها الموجة أسفل السلسلة تساوي\(v = \sqrt{\frac{F_{T}}{\mu}} = \sqrt{\frac{mg}{\mu}}\) المعادلة 16.7. تحدد شروط الحدود المتماثلة (عقدة في كل طرف) الترددات المحتملة التي يمكن أن تثير الموجات الدائمة. بدءًا من تردد صفر وزيادة التردد ببطء، يظهر الوضع الأول n = 1 كما هو موضح في الشكل\(\PageIndex{5}\). يُظهر الوضع الأول، الذي يُطلق عليه أيضًا الوضع الأساسي أو التوافقي الأول، أن نصف الطول الموجي قد تشكل، وبالتالي فإن الطول الموجي يساوي ضعف الطول بين العقد\(\lambda_{1}\) = 2L. التردد الأساسي، أو التردد التوافقي الأول، الذي يحرك هذا الوضع هو
\[f_{1} = \frac{v}{\lambda_{1}} = \frac{v}{2L},\]
حيث تكون سرعة الموجة v =\(\sqrt{\frac{F_{T}}{\mu}}\). يؤدي الحفاظ على ثبات التوتر وزيادة التردد إلى الوضع التوافقي الثاني أو الوضع n = 2. هذا الوضع هو الطول الموجي الكامل\(\lambda_{2}\) = L والتردد هو ضعف التردد الأساسي:
\[f_{2} = \frac{v}{\lambda_{2}} = \frac{v}{L} = 2f_{1} \ldotp\]
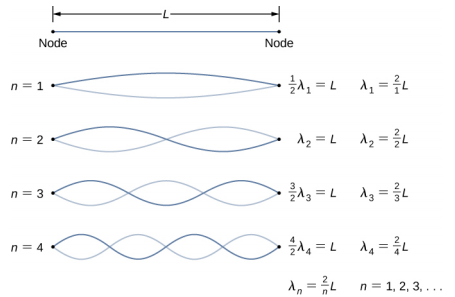
يحتوي الوضعان التاليان، أو التوافقيات الثالثة والرابعة، على أطوال موجية من\(\lambda_{3} = \frac{2}{3}\)\(\lambda_{4} = \frac{2}{4}\) L و L، مدفوعة بترددات f 3\(\frac{3v}{2L}\) = = 3f 1 و f 4\(\frac{4v}{2L}\) = 4f 1. تُعرف جميع الترددات فوق التردد f1 باسم الإيحاءات. يمكن تلخيص معادلات الطول الموجي والتردد على النحو التالي:
\[\lambda_{n} = \frac{2}{n} L \quad n = 1, 2, 3, 4, 5 \ldots \label{16.15}\]
\[f_{n} = n \frac{v}{2L} = nf_{1} \quad n = 1, 2, 3, 4, 5 \ldots \label{16.16}\]
وتُعرف أنماط الموجة الدائمة الممكنة للخيط، والتي تظهر الأربعة الأولى منها في الشكل\(\PageIndex{5}\)، بالأوضاع العادية، مع الترددات المعروفة بالترددات العادية. باختصار، يُطلق على التردد الأول لإنتاج الوضع العادي التردد الأساسي (أو التوافقي الأول). أي ترددات أعلى من التردد الأساسي هي إيحاءات. التردد الثاني للوضع العادي n = 2 للسلسلة هو النغمة الأولى (أو التوافقية الثانية). تردد الوضع العادي n = 3 هو النغمة الثانية (أو التوافقية الثالثة) وهكذا.
الحلول الموضحة كالمعادلة\ ref {16.15} والمعادلة\ ref {16.16} هي لسلسلة ذات شرط حدود العقدة في كل طرف. عندما تكون حالة الحدود على كلا الجانبين هي نفسها، يُقال أن النظام يحتوي على شروط حدودية متماثلة. المعادلة\ ref {16.15} والمعادلة\ ref {16.16} جيدة لأي شروط حدودية متماثلة، أي العقد في كلا الطرفين أو مضادات في كلا الطرفين.
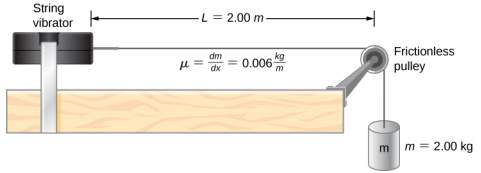
ضع في اعتبارك سلسلة من L = 2.00 متر متصلة بهزاز ذو سلسلة تردد قابل للتعديل كما هو موضح في الشكل\(\PageIndex{6}\). تنتقل الموجات التي ينتجها الهزاز إلى أسفل الخيط وتنعكس في حالة الحدود الثابتة في البكرة. يتم تمرير الخيط، الذي تبلغ كثافة كتلته الخطية\(\mu\) = 0.006 كجم/م، فوق بكرة غير احتكاكية ذات كتلة ضئيلة، ويتم توفير الشد بواسطة كتلة معلقة تبلغ 2.00 كجم. (أ) ما سرعة الموجات على الوتر؟ (ب) ارسم رسمًا تخطيطيًا للأنماط العادية الثلاثة الأولى للموجات الراكدة التي يمكن إنتاجها على الخيط وقم بتسمية كل منها بطول الموجة. (ج) ضع قائمة بالترددات التي يجب ضبط الهزاز الوتري عليها لإنتاج الأنماط العادية الثلاثة الأولى للموجات الراكدة.
إستراتيجية
- يمكن العثور على سرعة الموجة باستخدام v =\(\sqrt{\frac{F_{T}}{\mu}}\). يتم توفير التوتر من خلال وزن الكتلة المعلقة.
- تعتمد الموجات الدائمة على ظروف الحدود. يجب أن تكون هناك عقدة في كل طرف. سيكون الوضع الأول نصف الموجة. يمكن العثور على الثانية بإضافة نصف طول موجة. هذا هو أقصر طول سيؤدي إلى عقدة عند الحدود. على سبيل المثال، ستؤدي إضافة ربع الطول الموجي إلى ظهور مضاد عند الحدود وليس وضعًا يلبي شروط الحدود. يظهر هذا في الشكل\(\PageIndex{7}\).
- نظرًا لأن سرعة الموجة هي الطول الموجي مضروبًا في التردد، فإن التردد هو سرعة الموجة مقسومًا على الطول الموجي.

الحل
- ابدأ بسرعة الموجة على الخيط. التوتر يساوي وزن الكتلة المعلقة. يتم إعطاء كثافة الكتلة الخطية وكتلة الكتلة المعلقة: $v =\ sqrt {\ frac {F_ {T} {\ mu} =\ sqrt {\ frac {\ mu} =\ sqrt {\ mu} =\ sqrt {\\ frac {\؛ (2\؛ كغ) (9.8\؛ م/ث)} {0.006\؛ كغ/م} = 57.15\؛ م/ثانية\ ldo$$
- الوضع العادي الأول الذي يحتوي على عقدة في كل طرف هو نصف طول الموجة. يتم العثور على الوضعين التاليين بإضافة نصف الطول الموجي.
- تم العثور على ترددات الأوضاع الثلاثة الأولى باستخدام f =\(\frac{v_{w}}{\lambda}\). $$\ ابدأ {الانقسام} f_ {1} & =\ frac {w} {w} {\ lambda_ {1}} =\ فراك {57.15\؛ م/ث} {4.00\؛ م} = 14.29\؛ هرتز\\ f_ {2} و =\ frac {v_ {v_ {v_ {v_ {w}} {\ lambda_ {2}} =\ frac {v_ {v_ {v_ {w}} {\ lambda_ {2}} =; م/ث} {2.00\; م} = 28.58\; هرتز\\ f_ {3} & =\ فراك {v_ {v_ {w}} {\ لامدا _ {3}} =\ فراك {57.15\; م/ثانية} {1.333\; م} = 42.87\; هرتز\ نهاية {الانقسام} $$
الأهمية
تم إنتاج أوضاع الوقوف الثلاثة في هذا المثال من خلال الحفاظ على التوتر في السلسلة وضبط تردد القيادة. يؤدي الحفاظ على ثبات الشد في السلسلة إلى سرعة ثابتة. كان من الممكن إنتاج نفس الأنماط عن طريق الحفاظ على ثبات التردد وضبط سرعة الموجة في السلسلة (عن طريق تغيير الكتلة المعلقة.)
قم بزيارة هذه المحاكاة للعب بنظام 1-D أو ثنائي الأبعاد من مذبذبات الزنبرك الكتلي المقترن. قم بتغيير عدد الكتل، واضبط الشروط الأولية، وشاهد تطور النظام. شاهد طيف الأوضاع العادية للحركة التعسفية. شاهد الأوضاع الطولية أو العرضية في نظام 1-D.
معادلات الأطوال الموجية وترددات أنماط الموجة المنتجة على سلسلة:
\[\begin{split} \lambda_{n} & = \frac{2}{n} L \quad n = 1, 2, 3, 4, 5 \ldots and \\ f_{n} & = n \frac{v}{2L} = nf_{1} \quad n = 1, 2, 3, 4, 5 \ldots \end{split}\]
تم اشتقاقها من خلال النظر في موجة على سلسلة حيث توجد شروط حدودية متماثلة للعقدة في كل طرف. نتجت هذه الأنماط عن موجتين جيبيتين لهما خصائص متطابقة باستثناء تحركهما في اتجاهين متعاكسين، محصورتين في المنطقة L مع العقد المطلوبة في كلا الطرفين. هل ستنجح المعادلات نفسها إذا كانت هناك شروط حدودية متماثلة مع مضادات في كل طرف؟ كيف ستبدو الأنماط العادية للوسيط الذي يمكنه التذبذب بحرية في كل طرف؟ لا تقلق الآن إذا كنت لا تستطيع تخيل مثل هذا الوسيط، فما عليك سوى التفكير في وظيفتين للموجة الجيبية في منطقة طولها L، مع وجود مضادات في كل طرف.
قد يبدو من الصعب تصور شروط الحدود الحرة الموضحة في آخر «تحقق من فهمك». كيف يمكن أن يكون هناك نظام حر في التذبذب عند كل طرف؟ يظهر في الشكل\(\PageIndex{8}\) تكوينين محتملين لقضبان معدنية (كما هو موضح باللون الأحمر) متصلة بدعامتين (كما هو موضح باللون الأزرق). في الجزء (أ)، يتم دعم القضيب في الأطراف، وهناك شروط حدودية ثابتة عند كلا الطرفين. وبالنظر إلى التردد المناسب، يمكن توجيه القضيب إلى الرنين بطول موجة يساوي طول القضيب، مع وجود العقد في كل طرف. في الجزء (ب)، يتم دعم القضيب في مواضع ربع الطول من كل طرف من طرفي القضيب، وتوجد شروط حدودية حرة عند كلا الطرفين. نظرًا للتردد المناسب، يمكن أيضًا دفع هذا القضيب إلى الرنين بطول موجة يساوي طول القضيب، ولكن هناك مضادات في كل طرف. إذا كنت تواجه مشكلة في تصور الطول الموجي في هذا الشكل، تذكر أنه يمكن قياس الطول الموجي بين أقرب نقطتين متطابقتين وفكر في الشكل\(\PageIndex{9}\).
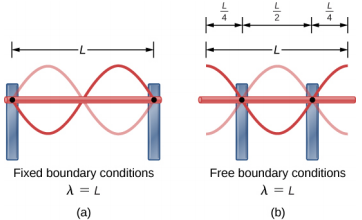
لاحظ أن دراسة الموجات الدائمة يمكن أن تصبح معقدة للغاية. في الشكل 16.32 (أ)، يظهر وضع n = 2 للموجة الدائمة، وينتج عنه طول موجة يساوي L. في هذا التكوين، كان وضع n = 1 ممكنًا أيضًا مع موجة دائمة تساوي 2 لتر. هل من الممكن الحصول على وضع n = 1 للتكوين الموضح في الجزء (ب)؟ الجواب هو لا. في هذا التكوين، هناك شروط إضافية تم وضعها خارج شروط الحدود. نظرًا لأن القضيب يتم تركيبه عند نقطة ربع الطول من كل جانب، يجب أن توجد عقدة هناك، وهذا يحد من الأنماط المحتملة للموجات الدائمة التي يمكن إنشاؤها. نترك الأمر كتمرين للقارئ للنظر فيما إذا كانت الأنماط الأخرى للموجات الدائمة ممكنة. وتجدر الإشارة إلى أنه عندما يتم تشغيل النظام بتردد لا يتسبب في رنين النظام، فقد تستمر الاهتزازات في الحدوث، ولكن سعة الاهتزازات ستكون أصغر بكثير من السعة عند الرنين.
يستخدم مجال الهندسة الميكانيكية الصوت الناتج عن الأجزاء المهتزة للأنظمة الميكانيكية المعقدة لاستكشاف مشاكل الأنظمة وإصلاحها. لنفترض أن جزءًا من السيارة يتردد عند تردد محرك السيارة، مما يتسبب في اهتزازات غير مرغوب فيها في السيارة. قد يتسبب هذا في فشل المحرك قبل الأوان. يستخدم المهندسون الميكروفونات لتسجيل الصوت الناتج عن المحرك، ثم يستخدمون تقنية تسمى تحليل فورييه للعثور على ترددات الصوت المنتجة بسعات كبيرة ثم ينظرون إلى قائمة أجزاء السيارة للعثور على جزء من شأنه أن يتردد صداه عند هذا التردد. قد يكون الحل بسيطًا مثل تغيير تركيبة المادة المستخدمة أو تغيير طول الجزء المعني.
هناك العديد من الأمثلة الأخرى للرنين في الموجات الدائمة في العالم المادي. يمكن دفع الهواء الموجود في الأنبوب، مثل الموجود في آلة موسيقية مثل الفلوت، إلى الرنين وإنتاج صوت لطيف، كما نناقش في Sound.
في أوقات أخرى، يمكن أن يسبب الرنين مشاكل خطيرة. توفر نظرة فاحصة على الزلازل دليلاً على الظروف المناسبة للرنين والأمواج الواقفة والتداخل البناء والمدمر. قد يهتز المبنى لعدة ثوانٍ بتردد قيادة يطابق تردد الاهتزاز الطبيعي للمبنى - مما ينتج عنه رنين يؤدي إلى انهيار مبنى واحد بينما لا تفعل المباني المجاورة ذلك. في كثير من الأحيان، يتم تدمير المباني ذات الارتفاع المحدد بينما تظل المباني الشاهقة الأخرى سليمة. يتطابق ارتفاع المبنى مع شرط إعداد موجة دائمة لهذا الارتفاع المحدد. إن امتداد السقف مهم أيضًا. غالبًا ما يُلاحظ أن صالات الألعاب الرياضية ومحلات السوبر ماركت والكنائس تتعرض لأضرار عندما تتعرض المنازل الفردية لأضرار أقل بكثير. يتردد صدى الأسقف ذات المساحات السطحية الكبيرة المدعومة فقط عند الحواف عند ترددات الزلازل، مما يتسبب في انهيارها. عندما تنتقل موجات الزلازل على طول سطح الأرض وتعكس الصخور الأكثر كثافة، يحدث التداخل البناء في نقاط معينة. في كثير من الأحيان لا تتضرر المناطق الأقرب إلى مركز الزلزال، بينما تتضرر المناطق البعيدة.


