16.6: تداخل الموجات
- Page ID
- 199842
- اشرح كيف تنعكس الموجات الميكانيكية وتنتقل عند حدود الوسيط
- حدد مصطلحي التداخل والتراكب
- أوجد الموجة الناتجة من موجتين جيبيتين متطابقتين تختلفان فقط في تغيير الطور
حتى الآن، كنا ندرس الموجات الميكانيكية التي تنتشر باستمرار عبر وسيط، لكننا لم نناقش ما يحدث عندما تواجه الموجات حدود الوسط أو ما يحدث عندما تواجه الموجة موجة أخرى تنتشر عبر نفس الوسط. تتفاعل الموجات مع حدود الوسيط، ويمكن أن تنعكس كل الموجة أو جزء منها. على سبيل المثال، عندما تقف على مسافة من وجه منحدر صلب وتصرخ، يمكنك سماع الموجات الصوتية تنعكس عن السطح الصلب كصدى. يمكن أن تتفاعل الموجات أيضًا مع الموجات الأخرى التي تنتشر في نفس الوسيط. إذا قمت برمي صخرتين في بركة على مسافة من بعضها البعض، يبدو أن التموجات الدائرية الناتجة عن الحجرين تمر عبر بعضها البعض أثناء انتشارها من حيث دخلت الأحجار الماء. وتعرف هذه الظاهرة بالتداخل. في هذا القسم، ندرس ما يحدث للموجات التي تواجه حدًا لوسط أو موجة أخرى تنتشر في نفس الوسط. سنرى أن سلوكهم مختلف تمامًا عن سلوك الجسيمات والأجسام الصلبة. في وقت لاحق، عندما ندرس الفيزياء الحديثة، سنرى أنه فقط على نطاق الذرات نرى أوجه تشابه في خصائص الموجات والجسيمات.
الانعكاس والإرسال
عندما تنتشر الموجة عبر وسيط، فإنها تنعكس عندما تواجه حدود الوسيط. تُعرف الموجة قبل الوصول إلى الحدود بموجة الحادث. تُعرف الموجة بعد مواجهة الحدود بالموجة المنعكسة. تعتمد كيفية انعكاس الموجة عند حدود الوسيط على ظروف الحدود؛ ستتفاعل الموجات بشكل مختلف إذا كانت حدود الوسيط ثابتة في مكانها أو حرة في الحركة (الشكل\(\PageIndex{1}\)). توجد حالة الحدود الثابتة عندما تكون الوسيطة عند الحدود ثابتة في مكانها بحيث لا يمكن تحريكها. توجد حالة الحدود الحرة عندما تكون الوسيطة عند الحدود حرة في التحرك.
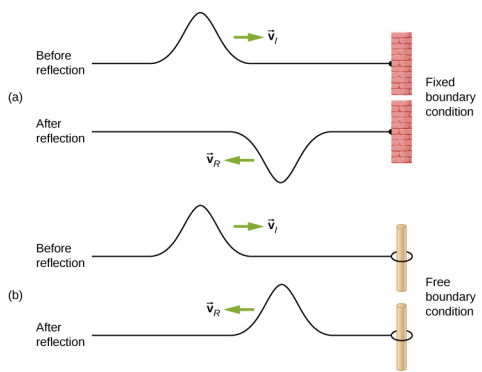
\(\PageIndex{1a}\)يوضح الشكل شرط الحدود الثابتة. هنا، يتم تثبيت أحد طرفي السلسلة على الحائط بحيث يتم تثبيت نهاية السلسلة في مكانها ولا يمكن للوسيط (السلسلة) عند الحدود التحرك. عندما تنعكس الموجة، يكون اتساع الطريقة المنعكسة هو بالضبط نفس سعة الموجة الساقطة، لكن الموجة المنعكسة تنعكس (\(180^o \pi\)راد) خارج الطور فيما يتعلق بالموجة الساقطة. يمكن تفسير تغيير الطور باستخدام قانون نيوتن الثالث: تذكر أن قانون نيوتن الثالث ينص على أنه عندما يمارس الجسم A قوة على الجسم B، فإن الجسم B يمارس قوة متساوية ومعاكسة على الجسم A. عندما تصطدم الموجة الساقطة بالجدار، يمارس الخيط قوة تصاعدية على الجدار ويتفاعل الجدار عن طريق ممارسة قوة متساوية ومعاكسة على الخيط. يتم عكس الانعكاس عند الحدود الثابتة. لاحظ أن الشكل يوضح قمة الموجة الساقطة المنعكسة في صورة قاع. إذا كانت الموجة الساقطة عبارة عن قاع منخفض، فستكون الموجة المنعكسة قمة.
\(\PageIndex{1b}\)يوضح الشكل حالة الحدود الحرة. هنا، يتم ربط أحد طرفي الخيط بحلقة صلبة ذات كتلة ضئيلة على عمود غير قابل للاحتكاك، وبالتالي فإن نهاية الخيط حرة في التحرك لأعلى ولأسفل. عندما تواجه موجة الحادث حدود الوسيط، تنعكس أيضًا. في حالة حالة الحدود الحرة، تكون الموجة المنعكسة في طور ما يتعلق بموجة الحادث. في هذه الحالة، تصطدم الموجة بالحدود الحرة من خلال تطبيق قوة تصاعدية على الحلقة، مما يؤدي إلى تسريع الحلقة. تنتقل الحلقة إلى أقصى ارتفاع يساوي سعة الموجة ثم تتسارع نحو موضع التوازن بسبب التوتر في الخيط. يوضح الشكل قمة الموجة الساقطة التي تنعكس في المرحلة فيما يتعلق بموجة الحادث كقمة. إذا كانت موجة الحادث منخفضة، فإن الموجة المنعكسة ستكون أيضًا منخفضة. سيكون اتساع الموجة المنعكسة مساويًا لسعة الموجة الساقطة.
في بعض الحالات، لا تكون حدود الوسيط ثابتة ولا مجانية. ضع في اعتبارك الشكل\(\PageIndex{2a}\)، حيث يتم ربط سلسلة ذات كثافة كتلة خطية منخفضة بسلسلة ذات كثافة كتلة خطية أعلى. في هذه الحالة، تكون الموجة المنعكسة خارج المرحلة فيما يتعلق بموجة الحادث. هناك أيضًا موجة مرسلة في طور ما يتعلق بموجة الحادث. كل من الموجات المرسلة والمنعكسة لها سعة أقل من سعة الموجة الساقطة. إذا كان التوتر هو نفسه في كلا السلسلتين، تكون سرعة الموجة أعلى في السلسلة ذات الكثافة الكتلية الخطية المنخفضة.
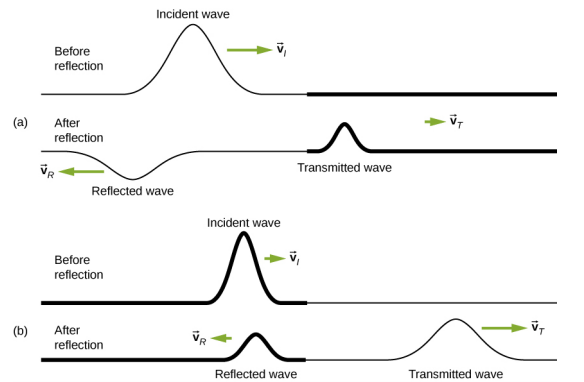
\(\PageIndex{2b}\)يُظهر سلسلة كثافة كتلة خطية عالية مرتبطة بسلسلة ذات كثافة خطية أقل. في هذه الحالة، تكون الموجة المنعكسة في طور ما يتعلق بموجة الحادث. هناك أيضًا موجة مرسلة في طور ما يتعلق بموجة الحادث. كل من الحادثة والموجات المنعكسة لهما سعة أقل من سعة الموجة الساقطة. قد تلاحظ هنا أنه إذا كان التوتر هو نفسه في كلا السلسلتين، فإن سرعة الموجة تكون أعلى في السلسلة ذات الكثافة الكتلية الخطية المنخفضة.
التراكب والتداخل
معظم الموجات لا تبدو بسيطة للغاية. الموجات المعقدة أكثر إثارة للاهتمام، بل إنها جميلة، لكنها تبدو هائلة. تتكون الموجات الميكانيكية الأكثر إثارة للاهتمام من مزيج من موجتين متحركتين أو أكثر تنتشر في نفس الوسط. يمكن استخدام مبدأ التراكب لتحليل مزيج الموجات.
ضع في اعتبارك أن نبضين بسيطين لهما نفس السعة يتحركان باتجاه بعضهما البعض في نفس الوسط، كما هو موضح في الشكل\(\PageIndex{3}\). في النهاية، تتداخل الموجات، وتنتج موجة تبلغ سعتها ضعف السعة، ثم تستمر دون أن تتأثر بالتلاقي. ويقال أن النبضات تتداخل، وتعرف هذه الظاهرة باسم التداخل.
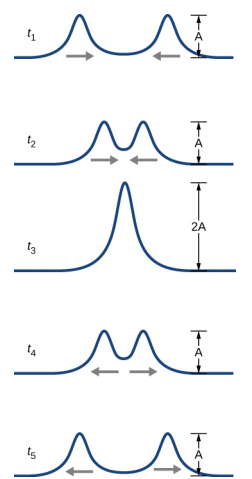
لتحليل تداخل موجتين أو أكثر، نستخدم مبدأ التراكب. بالنسبة للموجات الميكانيكية، ينص مبدأ التراكب على أنه إذا اجتمعت موجتان متحركتان أو أكثر في نفس النقطة، فإن الموضع الناتج لعنصر الكتلة في الوسط، عند هذه النقطة، هو المجموع الجبري للموضع بسبب الموجات الفردية. تظهر هذه الخاصية من خلال العديد من الموجات التي تمت ملاحظتها، مثل الموجات على الخيط، والموجات الصوتية، وموجات المياه السطحية. تخضع الموجات الكهرومغناطيسية أيضًا لمبدأ التراكب، ولكن تتم إضافة المجالات الكهربائية والمغناطيسية للموجة المدمجة بدلاً من إزاحة الوسط. الموجات التي تخضع لمبدأ التراكب هي موجات خطية؛ ويقال إن الموجات التي لا تخضع لمبدأ التراكب هي موجات غير خطية. في هذا الفصل، نتعامل مع الموجات الخطية، وخاصة الموجات الجيبية.
يمكن فهم مبدأ التراكب من خلال النظر في معادلة الموجة الخطية. في رياضيات الموجة، عرّفنا الموجة الخطية بأنها الموجة التي يخضع تمثيلها الرياضي لمعادلة الموجة الخطية. بالنسبة للموجة العرضية على سلسلة ذات قوة استعادة مرنة، تكون معادلة الموجة الخطية
\[\frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}} \ldotp\]
أي دالة موجة y (x، t) = y (x vt)، حيث تكون وسيطة الدالة خطية (x vt) هي حل لمعادلة الموجة الخطية وهي دالة موجة خطية. إذا كانت وظائف الموجة y 1 (x، t) و y 2 (x، t) هي حلول لمعادلة الموجة الخطية، فإن مجموع الوظيفتين y 1 (x، t) + y 2 (x، t) هو أيضًا حل لمعادلة الموجة الخطية. عادةً ما تقتصر الموجات الميكانيكية التي تخضع للتراكب على الموجات ذات السعات الصغيرة فيما يتعلق بأطوال موجاتها. إذا كانت السعة كبيرة جدًا، يتم تشويه الوسيط بعد المنطقة التي تكون فيها قوة استعادة الوسيط خطية.
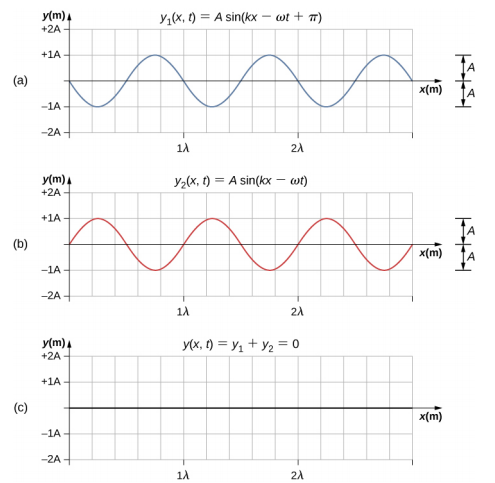
يمكن أن تتداخل الموجات بشكل بناء أو مدمر. \(\PageIndex{4}\)يوضح الشكل موجتين جيبيتين متطابقتين تصلان إلى نفس النقطة بالضبط في الطور. شكل\(\PageIndex{4a}\)\(\PageIndex{4b}\) وأظهر الموجتين الفرديتين،\(\PageIndex{4c}\) يوضح الشكل الموجة الناتجة عن المجموع الجبري للموجتين الخطيتين. يتم محاذاة قمم الموجتين بدقة، وكذلك الأحواض. ينتج عن هذا التراكب تداخلًا بناءً. ونظرًا لتفاقم الاضطرابات، ينتج التداخل البنائي موجة تبلغ ضعف سعة الموجات الفردية، ولكن لها نفس الطول الموجي.
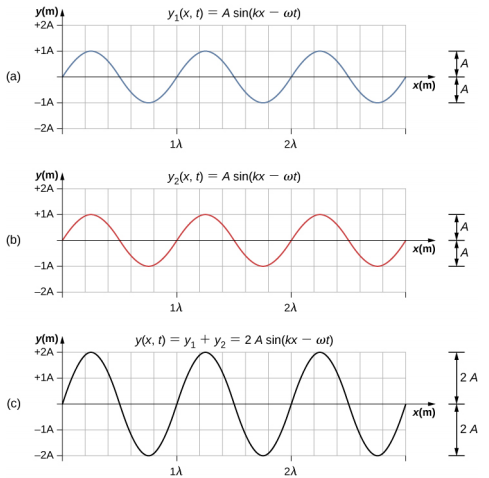
\(\PageIndex{5}\)يوضح الشكل موجتين متطابقتين تصلان تمامًا بزاوية 180 درجة خارج الطور، مما يؤدي إلى حدوث تداخل مدمر. قم\(\PageIndex{5a}\)\(\PageIndex{5b}\) بتشكيل وعرض الموجات الفردية، والشكل\(\PageIndex{5c}\) يوضح تراكب الموجتين. نظرًا لأن أحواض إحدى الموجات تضيف قمة الموجة الأخرى، فإن السعة الناتجة تكون صفرًا للتداخل المدمر - حيث يتم إلغاء الموجات تمامًا.
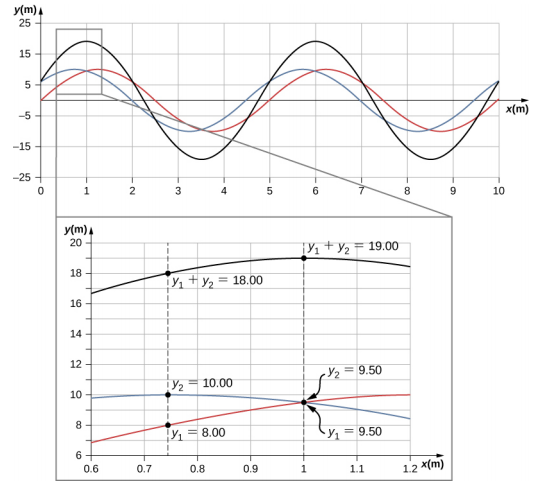
عندما تتداخل الموجات الخطية، تكون الموجة الناتجة مجرد المجموع الجبري للموجات الفردية كما هو مذكور في مبدأ التراكب. \(\PageIndex{6}\)يوضح الشكل موجتين (حمراء وزرقاء) والموجة الناتجة (سوداء). الموجة الناتجة هي المجموع الجبري للموجتين الفرديتين.
ينتج تراكب معظم الموجات مزيجًا من التداخل البناء والمدمر، ويمكن أن يختلف من مكان إلى آخر ومن وقت لآخر. يمكن أن يكون الصوت الصادر من الاستريو، على سبيل المثال، مرتفعًا في مكان ما وهادئًا في مكان آخر. ارتفاع الصوت يعني أن الموجات الصوتية تضيف جزئيًا بشكل بناء وجزئيًا بشكل مدمر في مواقع مختلفة. يحتوي الاستريو على مكبري صوت على الأقل لإنشاء موجات صوتية، ويمكن أن تنعكس الموجات من الجدران. تتداخل كل هذه الموجات، والموجة الناتجة هي تراكب الأمواج.
لقد أظهرنا عدة أمثلة لتراكب الموجات المتشابهة. \(\PageIndex{7}\)يوضح الشكل مثالاً لتراكب موجتين مختلفتين. وهنا مرة أخرى، تتفاقم الاضطرابات، مما ينتج عنه موجة.
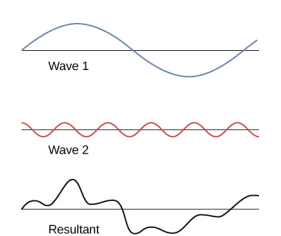
في بعض الأحيان، عندما تتداخل موجتان ميكانيكيتان أو أكثر، يمكن أن يكون النمط الناتج عن الموجة الناتجة غنيًا بالتعقيد، وبعضها بدون أي أنماط يمكن تمييزها بسهولة. على سبيل المثال، يمكن أن يبدو تخطيط الموجة الصوتية لموسيقاك المفضلة معقدًا للغاية وهو عبارة عن تراكب الموجات الصوتية الفردية من العديد من الآلات؛ إنه التعقيد الذي يجعل الموسيقى مثيرة للاهتمام وتستحق الاستماع إليها. في أوقات أخرى، يمكن أن تتداخل الموجات وتنتج ظواهر مثيرة للاهتمام، وهي معقدة في مظهرها ولكنها جميلة في بساطة المبدأ المادي للتراكب، الذي شكل الموجة الناتجة. ومن الأمثلة على ذلك الظاهرة المعروفة باسم الموجات الدائمة، التي تنتجها موجتان متطابقتان تتحركان في اتجاهات مختلفة. سننظر عن كثب في هذه الظاهرة في القسم التالي.
جرب هذه المحاكاة لعمل موجات باستخدام صنبور تقطير أو مكبر صوت أو ليزر! أضف مصدرًا ثانيًا أو زوجًا من الشقوق لإنشاء نمط تداخل. يمكنك ملاحظة مصدر واحد أو مصدرين. باستخدام مصدرين، يمكنك ملاحظة أنماط التداخل الناتجة عن تغيير الترددات وسعة المصادر.
تراكب الموجات الجيبية التي تختلف باختلاف الطور
تتكون العديد من الأمثلة في الفيزياء من موجتين جيبيتين متطابقتين في السعة ورقم الموجة والتردد الزاوي، ولكنها تختلف باختلاف الطور:
\[\begin{split} y_{1} (x,t) & = A \sin (kx - \omega t + \phi), \\ y_{2} (x,t) & = A \sin (kx - \omega t) \ldotp \end{split}\]
عندما توجد هاتان الموجتان في نفس الوسط، تكون الموجة الناتجة عن تراكب الموجتين الفرديتين هي مجموع الموجتين الفرديتين:
\[y_{R} (x,t) = y_{1} (x,t) + y_{2} (x,t) = A \sin(kx - \omega t + \phi) + A \sin (kx - \omega t) \ldotp\]
يمكن فهم الموجة الناتجة بشكل أفضل باستخدام الهوية المثلثية:
\[\sin u + \sin v = 2 \sin \left(\dfrac{u + v}{2}\right) \cos \left(\dfrac{u - v}{2}\right),\]
حيث u = kx -\(\omega\) t +\(\phi\) و v = kx -\(\omega\) t وتصبح الموجة الناتجة
\[\begin{split} y_{R} (x,t) & = y_{1} (x,t) + y_{2} (x,t) = A \sin (kx - \omega t + \phi) + A \sin (kx - \omega t) \\ & = 2A \sin \left(\dfrac{(kx - \omega t + \phi) + (kx - \omega t)}{2}\right) \cos \left(\dfrac{(kx - \omega t + \phi) - (kx - \omega t)}{2}\right) \\ & = 2A \sin \left(kx - \omega t + \dfrac{\phi}{2}\right) \cos \left(\dfrac{\phi}{2}\right) \ldotp \end{split}\]
عادة ما تتم كتابة هذه المعادلة كـ
\[y_{R} (x,t) = 2A \cos \left(\dfrac{\phi}{2}\right) \sin \left(kx - \omega t + \dfrac{\phi}{2}\right) \ldotp \label{16.13}\]
للموجة الناتجة نفس رقم الموجة والتردد الزاوي، وسعة A R = [2A cos\(\left(\dfrac{\phi}{2}\right)\)]، وانتقال طور يساوي نصف تحول الطور الأصلي. يوضح الشكل أمثلة للموجات التي تختلف فقط في التحول الطوري\(\PageIndex{7}\).
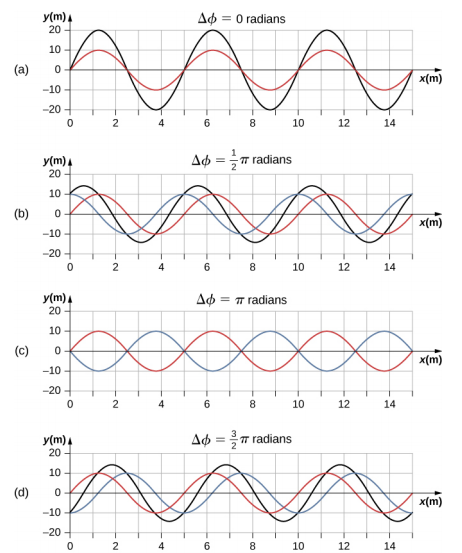
لكل من الموجات الحمراء والزرقاء نفس السعة ورقم الموجة والتردد الزاوي، وتختلف فقط في التحول الطوري. لذلك لديهم نفس الفترة والطول الموجي والتردد. الموجة الخضراء هي نتيجة تراكب الموجتين. عندما يكون للموجتين فرق طور قدره صفر، تكون الموجات في طور، ويكون للموجة الناتجة نفس رقم الموجة والتردد الزاوي، وسعة تساوي ضعف السعة الفردية (الجزء (أ)). هذا تدخل بناء. إذا كان فرق الطور 180 درجة، فإن الموجات تتداخل في التداخل المدمر (الجزء (ج)). تبلغ سعة الموجة الناتجة صفرًا. ينتج عن أي اختلاف طوري آخر موجة بنفس رقم الموجة والتردد الزاوي مثل الموجتين الساقطتين ولكن مع تحول طوري\(\frac{\phi}{2}\) وسعة تساوي 2A cos\(\left(\dfrac{\phi}{2}\right)\). وترد الأمثلة في الجزأين (ب) و (د).


