16.5: طاقة الموجة وقوتها
- Page ID
- 199851
- شرح كيفية انتقال الطاقة بالنبض أو الموجة
- وصف، باستخدام تعبير رياضي، كيف تعتمد الطاقة في الموجة على سعة الموجة
تحمل جميع الموجات الطاقة، وفي بعض الأحيان يمكن ملاحظة ذلك بشكل مباشر. يمكن للزلازل أن تهز مدنًا بأكملها على الأرض، وتؤدي عمل آلاف الكرات المدمرة (الشكل\(\PageIndex{1}\)). يمكن أن تؤدي الأصوات العالية إلى سحق الخلايا العصبية في الأذن الداخلية، مما يتسبب في فقدان السمع الدائم. تستخدم الموجات فوق الصوتية للمعالجة الحرارية العميقة لسلالات العضلات. يمكن لشعاع الليزر أن يحرق الورم الخبيث. تمضغ موجات المياه الشواطئ.

في هذا القسم، ندرس التعبير الكمي للطاقة في الأمواج. سيكون هذا ذا أهمية أساسية في المناقشات اللاحقة للموجات، من الصوت إلى الضوء إلى ميكانيكا الكم.
الطاقة في الأمواج
ترتبط كمية الطاقة في الموجة بسعتها وترددها. تنتج الزلازل ذات السعة الكبيرة عمليات نزوح أرضية كبيرة. تتمتع الأصوات العالية بسعات عالية الضغط وتأتي من اهتزازات مصدر ذات سعة أكبر من الأصوات الناعمة. تعمل كاسحات المحيط الكبيرة على تحريك الشاطئ أكثر من تلك الصغيرة. خذ بعين الاعتبار مثال النورس وموجة الماء في وقت سابق من الفصل (الشكل 16.2.2). يتم العمل على طيور النورس بواسطة الموجة بينما يتحرك النورس لأعلى، مما يؤدي إلى تغيير طاقته الكامنة. كلما زادت السعة، زاد ارتفاع طائر النورس بواسطة الموجة وكلما زاد التغيير في الطاقة الكامنة.
تعتمد طاقة الموجة على كل من السعة والتردد. إذا كانت طاقة كل طول موجي تعتبر حزمة منفصلة من الطاقة، فإن الموجة عالية التردد ستوفر المزيد من هذه الحزم لكل وحدة زمنية مقارنة بموجة التردد المنخفض. سنرى أن متوسط معدل نقل الطاقة في الموجات الميكانيكية يتناسب مع كل من مربع السعة ومربع التردد. إذا كانت موجتان ميكانيكيتان لهما سعة متساوية، ولكن لموجة واحدة تردد يساوي ضعف تردد الأخرى، فإن الموجة ذات التردد العالي سيكون لها معدل نقل طاقة يساوي أربعة أضعاف معدل نقل الطاقة لموجة التردد المنخفض. وتجدر الإشارة إلى أنه على الرغم من أن معدل نقل الطاقة يتناسب مع كل من مربع السعة ومربع التردد في الموجات الميكانيكية، فإن معدل نقل الطاقة في الموجات الكهرومغناطيسية يتناسب مع مربع السعة، ولكنه مستقل عن التردد.
الطاقة في الأمواج
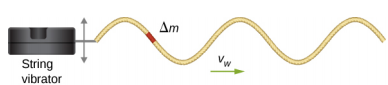
ضع في اعتبارك موجة جيبية على خيط ينتجه هزاز وتري، كما هو موضح في الشكل\(\PageIndex{2}\). الهزاز الوتري هو جهاز يهتز القضيب لأعلى ولأسفل. يتم ربط سلسلة ذات كثافة كتلة خطية منتظمة بالقضيب، ويقوم القضيب بتأرجح الخيط، مما ينتج عنه موجة جيبية. يعمل القضيب على الخيط وينتج طاقة تنتشر على طول الخيط. ضع في اعتبارك عنصر كتلة السلسلة الذي كتلته\(\Delta\) m، كما هو موضح في الشكل\(\PageIndex{2}\). عندما تنتشر الطاقة على طول الخيط، يتم دفع كل عنصر من عناصر الكتلة في السلسلة لأعلى ولأسفل بنفس تردد الموجة. يمكن تصميم كل عنصر من عناصر الكتلة في السلسلة كمذبذب توافقي بسيط. نظرًا لأن السلسلة لها كثافة خطية ثابتة\(\mu = \frac{\Delta m}{\Delta x}\)، فإن كل عنصر من عناصر الكتلة في السلسلة له الكتلة\(\Delta\) m =\(\mu \Delta\) x.
الطاقة الميكانيكية الكلية للموجة هي مجموع طاقتها الحركية والطاقة الكامنة. الطاقة الحركية K =\(\frac{1}{2}\) mv 2 لكل عنصر كتلة في سلسلة الطول\(\Delta\) x هي\(\Delta\) K =\(\frac{1}{2}\) (\(\Delta\)m) v y 2، حيث يتذبذب عنصر الكتلة عموديًا على اتجاه حركة الموجة. باستخدام كثافة الكتلة الخطية الثابتة، تكون الطاقة الحركية لكل عنصر من عناصر الكتلة في السلسلة بطول\(\Delta\) x
\[\Delta K = \frac{1}{2} (\mu \Delta x) v_{y}^{2} \ldotp \nonumber \]
يمكن تشكيل معادلة تفاضلية عن طريق السماح لطول عنصر الكتلة في السلسلة بالاقتراب من الصفر،
\[dK = \lim_{\Delta x \rightarrow 0} \frac{1}{2} (\mu \Delta x) v_{y}^{2} = \frac{1}{2} (\mu\; dx)v_{y}^{2} \ldotp \nonumber \]
نظرًا لأن الموجة عبارة عن موجة جيبية ذات تردد زاوي\(\omega\)، يمكن نمذجة موضع كل عنصر من عناصر الكتلة على النحو y (x، t) = A sin (kx −\(\omega\) t). يتذبذب كل عنصر من عناصر الكتلة في الوتر بسرعة v y\(\frac{\partial y(x,t)}{\partial t}\) = −A\(\omega\) cos (kx −\(\omega\) t). تصبح الطاقة الحركية لكل عنصر كتلة في السلسلة
\[\begin{split} dK & = \frac{1}{2} (\mu\; dx)[-A \omega \cos(kx - \omega t)]^{2} \\ & = \frac{1}{2} (\mu\; dx)[A^{2} \omega^{2} \cos^{2}(kx - \omega t)] \ldotp \end{split}\]
يمكن أن تكون الموجة طويلة جدًا وتتألف من العديد من الأطوال الموجية. لتوحيد الطاقة، ضع في اعتبارك الطاقة الحركية المرتبطة بطول موجة الموجة. يمكن دمج هذه الطاقة الحركية على طول الموجة للعثور على الطاقة المرتبطة بكل طول موجة من الموجة:
\[\begin{split} dK & = \frac{1}{2} (\mu\; dx)[A^{2} \omega^{2} \cos^{2}(kx - \omega t)] \\ \int_{0}^{K_{\lambda}} dK & = \int_{0}^{\lambda} \frac{1}{2} \mu A^{2} \omega^{2} \cos^{2}(kx - \omega t) dx = \frac{1}{2} \mu A^{2} \omega^{2} \int_{0}^{\lambda} \cos^{2} (kx) dx, \\ K_{lambda} & = \frac{1}{2} \mu A^{2} \omega^{2} \Big[ \frac{1}{2} x + \frac{1}{4k} \sin (2kx) \Big]_{0}^{\lambda} \\ & = \frac{1}{2} \mu A^{2} \omega^{2} \Big[ \frac{1}{2} \lambda + \frac{1}{4k} \sin (2k \lambda) - \frac{1}{4k} \sin(0) \Big] \\ & = \frac{1}{4} \mu A^{2} \omega^{2} \lambda \ldotp \end{split}\]
هناك أيضًا طاقة محتملة مرتبطة بالموجة. تشبه إلى حد كبير الكتلة التي تتأرجح في الزنبرك، هناك قوة استعادة متحفظة تؤدي، عندما يتم إزاحة عنصر الكتلة من موضع التوازن، إلى دفع عنصر الكتلة مرة أخرى إلى موضع التوازن. يمكن العثور على الطاقة الكامنة لعنصر الكتلة من خلال النظر في قوة الاستعادة الخطية للخيط، في التذبذبات، رأينا أن الطاقة الكامنة المخزنة في زنبرك بقوة استعادة خطية تساوي U =\(\frac{1}{2}\) k s x 2، حيث التوازن يُعرّف الموضع بأنه x = 0.00 m، وعندما تتأرجح كتلة متصلة بالزنبرك بحركة توافقية بسيطة، يكون التردد الزاوي مساويًا لـ\(\omega = \frac{k_{s}}{m}\). عندما يتذبذب كل عنصر من عناصر الكتلة في حركة توافقية بسيطة، فإن ثابت الزنبرك يساوي k s =\(\Delta\) m\(\omega^{2}\). الطاقة الكامنة لعنصر الكتلة تساوي
\[\Delta U = \frac{1}{2} k_{s} x^{2} = \frac{1}{2} \Delta m \omega^{2} x^{2} \ldotp \nonumber \]
لاحظ أن k s هو ثابت الزنبرك وليس رقم الموجة k =\(\frac{2 \pi}{\lambda}\). يمكن استخدام هذه المعادلة لإيجاد الطاقة على طول موجة. بالتكامل عبر الطول الموجي، يمكننا حساب الطاقة الكامنة عبر الطول الموجي:
\[\begin{split} dU & = \frac{1}{2} k_{s} x^{2} = \frac{1}{2} \mu \omega^{2} x^{2} dx, \\ U_{\lambda} & = \frac{1}{2} \mu \omega^{2} A^{2} \int_{0}^{\lambda} \sin^{2} (kx) dx = \frac{1}{4} \mu A^{2} \omega^{2} \lambda \ldotp \end{split}\]
الطاقة الكامنة المرتبطة بطول موجة الموجة تساوي الطاقة الحركية المرتبطة بطول موجة. الطاقة الكلية المرتبطة بالطول الموجي هي مجموع الطاقة الكامنة والطاقة الحركية:
\[\begin{split} E_{\lambda} & = U_{\lambda} +K_{\lambda} \\ & = \frac{1}{4} \mu A^{2} \omega^{2} \lambda + \frac{1}{4} \mu A^{2} \omega^{2} \lambda \\ & = \frac{1}{2} \mu A^{2} \omega^{2} \lambda \ldotp \end{split}\]
يمكن العثور على متوسط القوة الزمنية للموجة الميكانيكية الجيبية، وهو متوسط معدل نقل الطاقة المرتبط بالموجة أثناء مرورها بنقطة، عن طريق أخذ إجمالي الطاقة المرتبطة بالموجة مقسومًا على الوقت المستغرق لنقل الطاقة. إذا كانت سرعة الموجة الجيبية ثابتة، فإن الوقت الذي يمر فيه طول موجة واحدة بنقطة يساوي فترة الموجة، وهي أيضًا ثابتة. بالنسبة للموجة الميكانيكية الجيبية، فإن القدرة ذات متوسط الوقت هي الطاقة المرتبطة بطول موجة مقسومًا على فترة الموجة. الطول الموجي للموجة مقسومًا على الفترة يساوي سرعة الموجة،
\[P_{ave} = \frac{E_{\lambda}}{T} = \frac{1}{2} \mu A^{2} \omega^{2} \frac{\lambda}{T} = \frac{1}{2} \mu A^{2} \omega^{2} v \ldotp \label{16.10}\]
لاحظ أن هذه المعادلة لقوة متوسط الوقت للموجة الميكانيكية الجيبية تُظهر أن القوة تتناسب مع مربع سعة الموجة ومع مربع التردد الزاوي للموجة. تذكر أن التردد الزاوي يساوي\(\omega\) = 2\(\pi\) f، وبالتالي فإن قوة الموجة الميكانيكية تساوي مربع السعة ومربع تردد الموجة.
ضع في اعتبارك خيطًا طوله مترين وكتلته 70.00 جم متصل بهزاز خيطي كما هو موضح في الشكل\(\PageIndex{2}\). يبلغ الشد في الخيط 90.0 نيوتن. وعندما يتم تشغيل الهزاز الوتري، فإنه يتأرجح بتردد 60 هرتز وينتج موجة جيبية على الوتر بسعة 4.00 سم وسرعة موجة ثابتة. ما متوسط القدرة التي يوفرها الهزاز الوتري للموجة؟
إستراتيجية
يجب أن تساوي الطاقة التي يتم توفيرها للموجة قوة متوسط الوقت للموجة على السلسلة. نحن نعرف كتلة السلسلة (m s)، وطول السلسلة (L s)، والتوتر (F T) في السلسلة. يمكن اشتقاق سرعة الموجة على الخيط من كثافة الكتلة الخطية والتوتر. تتأرجح السلسلة بنفس تردد الهزاز الوتري، والذي يمكننا من خلاله العثور على التردد الزاوي.
الحل
- ابدأ بمعادلة متوسط القوة الزمنية للموجة الجيبية على السلسلة: $$P =\ frac {1} {2}\ mu A^ {2}\ omega^ {2} v\ ldotP$$يتم إعطاء السعة، لذلك نحتاج إلى حساب كثافة الكتلة الخطية للخيط، والتردد الزاوي للموجة على الوتر، وسرعة الموجة على الوتر.
- نحتاج إلى حساب الكثافة الخطية للعثور على سرعة الموجة: $$\ mu =\ frac {m_ {s}} {L_ {s}} =\ frac {0.070\; kg} {2.00\; m} = 0.035\; kg/m\ ldotp$$
- يمكن العثور على سرعة الموجة باستخدام كثافة الكتلة الخطية وتوتر السلسلة: $v =\ sqrt {\ frac {F_ {T}} {\ mu} =\ sqrt {\ frac {90.00\; N} {0.035\; كجم/م} = 50.71\; م/ث\ ldotp$$
- يمكن العثور على التردد الزاوي من التردد: $$\ أوميغا = 2\ pi f = 2\ pi (60\; s^ {-1}) = 376.80\; s^ {-1}\ ldotp$$
- احسب متوسط القدرة الزمنية: $P =\ frac {1} {2}\ مو A^ {2}\ أوميغا ^ {2} v =\ frac {1} {2} (0.035\؛ كغم/م) (0.040\؛ م) ^ {2} (376.80\؛ s ^ {-1}) ^ {2} (50.71\؛ م/ث) = 201.5\؛ W\ ldotp $$
الأهمية
تتناسب قوة متوسط الوقت للموجة الجيبية مع مربع سعة الموجة ومربع التردد الزاوي للموجة. هذا صحيح بالنسبة لمعظم الموجات الميكانيكية. إذا تضاعف التردد الزاوي أو سعة الموجة، فستزيد القدرة بعامل أربعة. تتناسب قوة متوسط الوقت للموجة على السلسلة أيضًا مع سرعة الموجة الجيبية على السلسلة. إذا تضاعفت السرعة، بزيادة التوتر بعامل أربعة، فستتضاعف القوة أيضًا.
هل القدرة ذات المتوسط الزمني للموجة الجيبية على سلسلة تتناسب مع الكثافة الخطية للخيط؟
تم اشتقاق معادلات طاقة الموجة وقوة متوسط الوقت للموجة الجيبية على سلسلة. بشكل عام، تتناسب طاقة الموجة الميكانيكية والقوة مع مربع السعة ومع مربع التردد الزاوي (وبالتالي مربع التردد).
ميزة أخرى مهمة للموجات هي شدة الأمواج. يمكن أيضًا تركيز الموجات أو انتشارها. فموجات الزلزال، على سبيل المثال، تنتشر على مساحة أكبر أثناء ابتعادها عن المصدر، بحيث تقل ضررها كلما ابتعدت عن المصدر. تغيير المنطقة التي تغطيها الأمواج له تأثيرات مهمة. يتم تضمين جميع هذه العوامل ذات الصلة في تعريف الكثافة (I) كقوة لكل وحدة مساحة:
\[I = \frac{P}{A}, \label{16.11}\]
حيث P هي القدرة التي تنقلها الموجة عبر المنطقة A. ينطبق تعريف الكثافة على أي طاقة تمر بمرحلة انتقال، بما في ذلك تلك التي تنقلها الأمواج. وحدة SI للكثافة هي واط لكل متر مربع (W/m 2). العديد من الموجات هي موجات كروية تخرج من المصدر ككرة. على سبيل المثال، قد ينتج مكبر صوت مثبت على عمود فوق الأرض موجات صوتية تبتعد عن المصدر كموجة كروية. تتم مناقشة الموجات الصوتية بمزيد من التفصيل في الفصل التالي، ولكن بشكل عام، كلما ابتعدت عن السماعة، قلت كثافة الصوت الذي تسمعه. عندما تخرج موجة كروية من مصدر، تزداد مساحة سطح الموجة كلما زاد نصف القطر (A = 4\(\pi\) r 2). وبالتالي فإن شدة الموجة الكروية هي
\[I = \frac{P}{4 \pi r^{2}} \ldotp \label{16.12}\]
إذا لم تكن هناك قوى تبديد، فستظل الطاقة ثابتة مع تحرك الموجة الكروية بعيدًا عن المصدر، لكن الكثافة ستنخفض مع زيادة مساحة السطح.
في حالة الموجة الدائرية ثنائية الأبعاد، تتحرك الموجة للخارج، مما يزيد من محيط الموجة مع زيادة نصف قطر الدائرة. إذا قمت بإلقاء حصاة في بركة، فإن تموج السطح يتحرك كموجة دائرية. عندما يتحرك التموج بعيدًا عن المصدر، تنخفض السعة. تنتشر طاقة الموجة حول محيط أكبر وتتناقص السعة\(\frac{1}{r}\) بما يتناسب مع الموجة الكروية وليس كذلك\(\frac{1}{r^{2}}\).


