16.4: سرعة الموجة على خيط ممتد

Last updated
Save as PDF

Page ID: 199857

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

أهداف التعلم

حدد العوامل التي تؤثر على سرعة الموجة على السلسلة
اكتب تعبيرًا رياضيًا لسرعة الموجة على سلسلة وقم بتعميم هذه المفاهيم للوسائط الأخرى

تعتمد سرعة الموجة على خصائص الوسيط. على سبيل المثال، في حالة الغيتار، تهتز الأوتار لإنتاج الصوت. تحدد سرعة الموجات على الأوتار والطول الموجي تردد الصوت الناتج. تختلف سماكة الأوتار الموجودة على الجيتار ولكنها قد تكون مصنوعة من مواد مماثلة. لها كثافات خطية مختلفة، حيث يتم تعريف الكثافة الخطية على أنها الكتلة لكل طول،

\[\mu = \frac{\text{mass of string}}{\text{length of string}} = \frac{m}{l} \ldotp \label{16.7}\]

في هذا الفصل، ننظر فقط إلى السلسلة ذات الكثافة الخطية الثابتة. إذا كانت الكثافة الخطية ثابتة، فإن الكتلة ($\Delta m$) لطول السلسلة الصغيرة ($\Delta$x) هي$\Delta m = \mu \Delta x$. على سبيل المثال، إذا كان طول الخيط 2.00 متر وكتلته 0.06 كجم، فإن الكثافة الخطية هي$\mu = \frac{0.06\; kg}{2.00\; m}$ = 0.03 كجم/م، وفي حالة قطع مقطع طوله 1.00 مم من الخيط، تكون كتلة الطول 1.00 مم

\[ \Delta m = \mu \Delta x = (0.03\, kg/m)(0.001\, m) = 3.00 \times 10^{−5}\, kg. \nonumber\]

يحتوي الجيتار أيضًا على طريقة لتغيير توتر الأوتار. يتم ضبط شد الأوتار عن طريق تدوير المغزل، الذي يسمى أوتاد الضبط، والتي يتم لف الأوتار حولها. بالنسبة للغيتار، تحدد الكثافة الخطية للخيط والتوتر في الوتر سرعة الموجات في الوتر ويتناسب تردد الصوت الناتج مع سرعة الموجة.

سرعة الموجة على خيط تحت التوتر

لمعرفة كيف تعتمد سرعة الموجة على الخيط على التوتر والكثافة الخطية، ضع في اعتبارك النبض المرسل عبر خيط مشدود (الشكل$\PageIndex{1}$). عندما يكون الخيط المشدود في وضع الاتزان في وضع الاتزان،$F_T$ يكون الشد في الخيط ثابتًا. ضع في اعتبارك عنصرًا صغيرًا من السلسلة بكتلة تساوي$\Delta m = \mu \Delta x$. يكون عنصر الكتلة في حالة السكون وفي حالة توازن وقوة التوتر على جانبي عنصر الكتلة متساوية ومتعاكسة.

يعرض الشكل مقطعًا من سلسلة مع تمييز جزء واحد. يُطلق على طول الجزء المميز اسم delta x. يشير سهمان من هذا الجزء في اتجاهين متعاكسين بطول السلسلة. ويطلق على هذه الكلمات اسم F. الجزء المميز يسمى دلتا m يساوي mu delta x. — الشكل$\PageIndex{1}$: عنصر الكتلة في الخيط يظل مشدودًا مع الشد$F_T$. يكون عنصر الكتلة في حالة توازن ثابت، وقوة التوتر المؤثرة على جانبي عنصر الكتلة متساوية في الحجم والعكس في الاتجاه.

في حالة سحب خيط تحت الشد، تتحرك موجة عرضية في الاتجاه السيني الموجب، كما هو موضح في الشكل$\PageIndex{2}$. عنصر الكتلة صغير ولكن يتم تكبيره في الشكل لجعله مرئيًا. يتذبذب عنصر الكتلة الصغيرة عموديًا على حركة الموجة نتيجة لقوة الاستعادة التي توفرها السلسلة ولا يتحرك في الاتجاه x. يكون الشد F _T في الخيط، والذي يعمل في الاتجاه x الموجب والسالب، ثابتًا تقريبًا ومستقل عن الموضع والوقت.

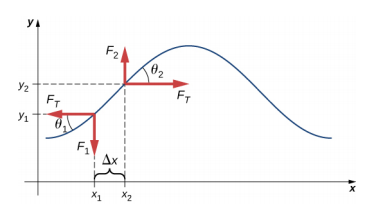
يوضح الشكل موجة النبض. يظهر سهمان على طول المنحدر التصاعدي للموجة، أحدهما يشير لأعلى ولليمين، والآخر يشير لأسفل ولليسار. تصنع هذه الأسهم، التي تحمل علامة F، زاويتين ثيتا 2 وثيتا 1 على التوالي بـ — الشكل$\PageIndex{2}$: ينتزع خيط تحت الشد، مما يتسبب في تحرك النبض على طول الخيط في الاتجاه السيني الموجب.

افترض أن ميل السلسلة التي تم إزاحتها بالنسبة للمحور الأفقي صغير. القوة الصافية على عنصر الخيط، التي تعمل بالتوازي مع السلسلة، هي مجموع الشد في الخيط وقوة الاستعادة. يتم إلغاء المكونات x لقوة الشد، وبالتالي فإن القوة الصافية تساوي مجموع مكونات y للقوة. حجم المكون x للقوة يساوي قوة الشد الأفقية للخيط$F_T$ كما هو موضح في الشكل$\PageIndex{2}$. للحصول على المكونات y للقوة، لاحظ أن tan$\theta_{1} = − \frac{F_{1}}{F_{T}}$ and$\tan \theta_{2} = \frac{F_{2}}{F_{T}}$. $\tan \theta$يساوي ميل الدالة عند نقطة، وهو ما يساوي المشتق الجزئي لـ y بالنسبة إلى x عند تلك النقطة. لذلك،$\frac{F_{1}}{F_{T}}$ يساوي المنحدر السالب للخيط عند x ₁$\frac{F_{2}}{F_{T}}$ ويساوي ميل السلسلة عند x ₂:

\[\frac{F_{1}}{F_{T}} = - \left(\dfrac{\partial y}{\partial x}\right)_{x_{1}}\; and\; \frac{F_{2}}{F_{T}} = \left(\dfrac{\partial y}{\partial x}\right)_{x_{2}} \ldotp\]

يمكن كتابة القوة الصافية الموجودة على عنصر الكتلة الصغيرة على النحو

\[F_{net} = F_{1} + F_{2} = F_{T} \Bigg[ \left(\dfrac{\partial y}{\partial x}\right)_{x_{2}} - \left(\dfrac{\partial y}{\partial x}\right)_{x_{1}} \Bigg] \ldotp\]

باستخدام قانون نيوتن الثاني، تساوي القوة الكلية الكتلة مضروبة في العجلة. الكثافة الخطية للسلسلة هي الكتلة لكل طول من السلسلة، وكتلة جزء السلسلة هي$\mu \Delta$ x،

\[F_{T} \Bigg[ \left(\dfrac{\partial y}{\partial x}\right)_{x_{2}} - \left(\dfrac{\partial y}{\partial x}\right)_{x_{1}} \Bigg] = \Delta ma = \mu \Delta x \left(\frac{\partial^{2} y}{\partial t^{2}}\right) \ldotp\]

القسمة _{على F T}$\Delta$ x وأخذ الحد عند اقتراب$\Delta$ x من الصفر،

\[\begin{split} \lim_{\Delta x \rightarrow 0} \frac{\Bigg[ \left(\dfrac{\partial y}{\partial x}\right)_{x_{2}} - \left(\dfrac{\partial y}{\partial x}\right)_{x_{1}} \Bigg]}{\Delta x} & = \frac{\mu}{F_{T}} \frac{\partial^{2} y}{\partial t^{2}} \\ \frac{\partial^{2} y}{\partial x^{2}} & = \frac{\mu}{F_{T}} \frac{\partial^{2} y}{\partial t^{2}} \ldotp \end{split}\]

تذكر أن معادلة الموجة الخطية هي

\[\frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}} \ldotp\]

لذلك،

\[\frac{1}{v^{2}} = \frac{\mu}{F_{T}} \ldotp\]

لحل المشكلة$v$، نرى أن سرعة الموجة على الخيط تعتمد على التوتر والكثافة الخطية.

سرعة الموجة على خيط تحت الشد

يمكن العثور على سرعة النبض أو الموجة على سلسلة تحت التوتر باستخدام المعادلة

\[|v| = \sqrt{\frac{F_{T}}{\mu}} \label{16.8}\]

$F_T$أين الشد في الخيط$µ$ وهي الكتلة لكل طول من الخيط.

مثال 16.5: سرعة موجة زنبرك الجيتار

في غيتارة ذات ستة أوتار، تبلغ الكثافة الخطية للخيط E المرتفع$\mu_{High\; E}$ = 3.09 × 10 ⁻⁴ كجم/م، بينما تبلغ كثافة السلسلة E المنخفضة$\mu_{Low\; E}$ = 5.78 × 10 ⁻³ كجم/م. (أ) إذا تم قطع سلسلة E العالية، مما أدى إلى ظهور موجة في الوتر، فما سرعة الموجة إذا كانت شدة الوتر هي 56.40 نيوتن؟ (ب) تكون الكثافة الخطية للسلسلة E المنخفضة أكبر بحوالي 20 مرة من كثافة السلسلة E العالية. لكي تنتقل الموجات عبر سلسلة E المنخفضة بنفس سرعة الموجة مثل E العالية، هل يجب أن يكون التوتر أكبر أو أصغر من سلسلة E العالية؟ ماذا سيكون التوتر التقريبي؟ (ج) احسب توتر السلسلة E المنخفضة اللازمة لنفس سرعة الموجة.

إستراتيجية

يمكن العثور على سرعة الموجة من الكثافة الخطية والتوتر$v = \sqrt{\frac{F_{T}}{\mu}}$.
من المعادلة v =$\sqrt{\frac{F_{T}}{\mu}}$، إذا زادت الكثافة الخطية بعامل 20 تقريبًا، فسيتعين زيادة التوتر بعامل 20.
بمعرفة السرعة والكثافة الخطية، يمكن حل معادلة السرعة لقوة التوتر F _T =$\mu$ v ².

الحل

استخدم معادلة السرعة للعثور على السرعة: $v =\ sqrt {\ frac {F_ {T}} {\ مو} =\ sqrt {\ frac {56.40\; N} {3.09\ مرات 10^ {-4}\; كجم/م} = 427.23\; م/ث\ ldotp$$
وسيتعين زيادة التوتر بعامل يبلغ حوالي 20. سيكون التوتر أقل بقليل من 1128 نيوتن.
استخدم معادلة السرعة للعثور على التوتر الفعلي: $F_ {T} =\ مو v^ {2} = (5.78\ مرات 10^ {-3}\؛ كجم/م) (427.23\؛ م/ث) ^ {2} = 1055.00\؛ N\ ldotp$$
يقع هذا الحل في حدود 7٪ من التقريب.

الدلالة

يتم ضبط النغمات القياسية للسلاسل الستة (عالية E، B، G، D، A، منخفضة E) للاهتزاز عند الترددات الأساسية (329.63 هرتز، 246.94 هرتز، 196.00 هرتز، 146.83 هرتز، 110.00 هرتز، 82.41 هرتز) عند التقاطها. تعتمد الترددات على سرعة الموجات على السلسلة والطول الموجي للموجات. السلاسل الستة لها كثافة خطية مختلفة ويتم «ضبطها» عن طريق تغيير التوترات في الأوتار. سنرى في تداخل الموجات أن الطول الموجي يعتمد على طول السلاسل وظروف الحدود. لتشغيل النوتات غير النوتات الأساسية، يتم تغيير أطوال الأوتار بالضغط على الأوتار.

التمرين 16.5

تعتمد سرعة موجة الموجة على الخيط على التوتر وكثافة الكتلة الخطية. إذا تضاعف الشد، فماذا يحدث لسرعة الموجات على الوتر؟

سرعة موجات الضغط في السائل

تعتمد سرعة الموجة على الخيط على الجذر التربيعي للتوتر مقسومًا على الكتلة لكل طول، وهي الكثافة الخطية. بشكل عام، تعتمد سرعة الموجة عبر الوسط على الخاصية المرنة للوسيط وخاصية القصور الذاتي للوسيط.

\[|v| = \sqrt{\frac{elastic\; property}{inertial\; property}}\]

تصف الخاصية المرنة ميل جزيئات الوسط للعودة إلى موضعها الأولي عند الاضطراب. تصف خاصية القصور الذاتي ميل الجسيم لمقاومة التغيرات في السرعة.

تعتمد سرعة الموجة الطولية عبر السائل أو الغاز على كثافة السائل والمعامل الأكبر للسائل،

\[v = \sqrt{\frac{\beta}{\rho}} \ldotp \label{16.9}\]

هنا يتم تعريف معامل الكتلة على أنه =$− \frac{\Delta P}{\frac{\Delta V}{V_{0}}}$، حيث$\Delta$ P هو التغيير في الضغط والمقام هو نسبة التغيير في الحجم إلى الحجم الأولي،$\rho \equiv \frac{m}{V}$ وهو الكتلة لكل وحدة حجم. على سبيل المثال، الصوت عبارة عن موجة ميكانيكية تنتقل عبر سائل أو مادة صلبة. سرعة الصوت في الهواء بضغط جوي يبلغ 1.013 × 10 ⁵ باسكال ودرجة حرارة 20 درجة مئوية هي v _s ≈ 343.00 m/s، ولأن الكثافة تعتمد على درجة الحرارة، فإن سرعة الصوت في الهواء تعتمد على درجة حرارة الهواء. سيتم مناقشة هذا بالتفصيل في Sound.