16.3: رياضيات الأمواج
- Page ID
- 199862
- قم بتمثيل موجة تتحرك بسرعة موجة ثابتة باستخدام تعبير رياضي
- احسب سرعة الوسيط وتسارعه
- أظهر كيف تختلف سرعة الوسط عن سرعة الموجة (سرعة الانتشار)
في القسم السابق، وصفنا الموجات الدورية من خلال خصائصها من حيث الطول الموجي والفترة والسعة وسرعة الموجة للموجة. يمكن أيضًا وصف الموجات بحركة جزيئات الوسط الذي تتحرك من خلاله الموجات. يمكن تصميم موضع جسيمات الوسط رياضيًا على أنه دالة الموجة s، والتي يمكن استخدامها للعثور على موضع وسرعة وتسارع جزيئات وسط الموجة في أي وقت.
نبضات
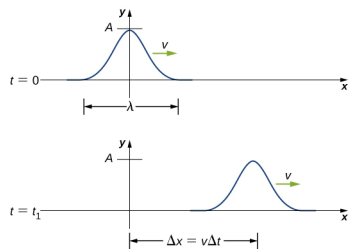
يمكن وصف النبض بأنه موجة تتكون من اضطراب واحد يتحرك عبر الوسط بسعة ثابتة. يتحرك النبض كنمط يحافظ على شكله أثناء انتشاره بسرعة موجة ثابتة. نظرًا لأن سرعة الموجة ثابتة، فإن المسافة التي تتحرك فيها النبضة في الوقت Δt تساوي Δx = vΔt (الشكل\(\PageIndex{1}\)).
نمذجة موجة جيبية أحادية البعد باستخدام دالة الموجة
ضع في اعتبارك خيطًا يتم الاحتفاظ به عند توتر مستمر\(F_T\) حيث يكون أحد الطرفين ثابتًا ويتأرجح الطرف الحر بين جهاز ميكانيكي\(y = +A\)\(y = −A\) وبواسطة جهاز ميكانيكي بتردد ثابت. \(\PageIndex{2}\)يعرض الشكل لقطات للموجة بفاصل زمني من ثمانية من الفترة، تبدأ بعد فترة واحدة (\(t = T\)).
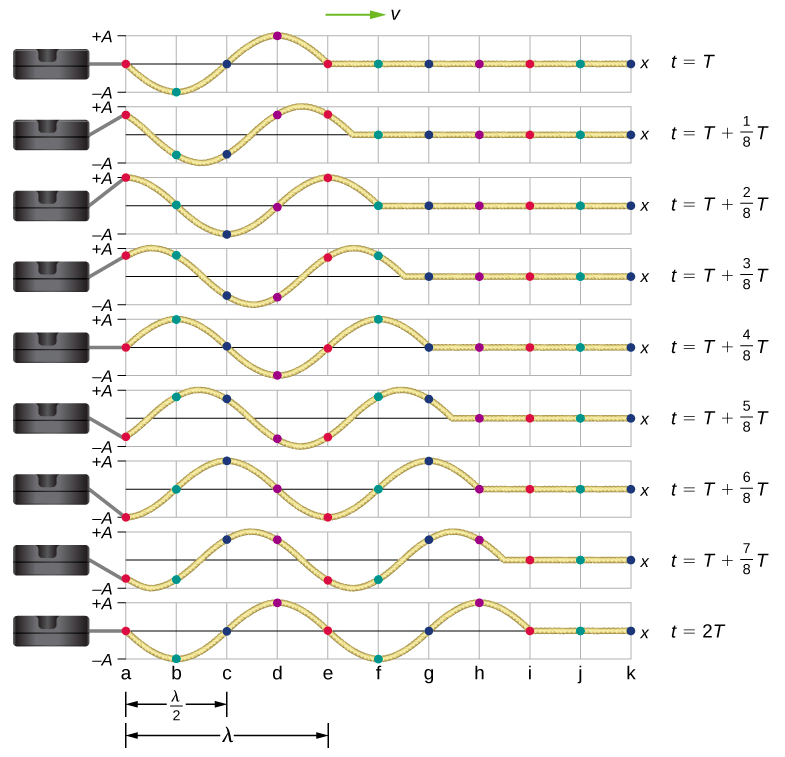
لاحظ أن كل نقطة اختيار على السلسلة (المميزة بنقاط ملونة) تتأرجح لأعلى ولأسفل بحركة توافقية بسيطة\(y = −A\)، بين\(y = +A\) نقطة وأخرى\(T\). تكون الموجة الموجودة على الوتر جيبية وتترجم في الاتجاه السيني الموجب مع تقدم الوقت.
في هذه المرحلة، من المفيد أن تتذكر من دراستك للجبر أنه إذا كانت دالة\(f(x)\) ما،\(f(x−d)\) فإن نفس الوظيفة تُترجم في الاتجاه السيني الموجب بمسافة\(d\). الدالة\(f(x+d)\) هي نفس الدالة المترجمة في اتجاه x السالب بمسافة\(d\). نريد تحديد دالة الموجة التي ستعطي\(y\) الموضع -لكل مقطع من السلسلة لكل موضع x على طول السلسلة في كل مرة\(t\).
عند النظر إلى اللقطة الأولى في الشكل\(\PageIndex{2}\)،\(x = λ\) يمكن تصميم موضع y للسلسلة بين\(x = 0\) و كدالة جيبية. تنتشر هذه الموجة أسفل السلسلة بطول موجة واحدة في فترة واحدة، كما هو موضح في اللقطة الأخيرة. لذلك تتحرك الموجة بسرعة موجة ثابتة تبلغ\(v = λ/T\).
تذكر أن دالة الجيب هي دالة للزاوية\(θ\) تتأرجح بين +1 و−1 وتكرر كل\(2π\) راديان (الشكل\(\PageIndex{3}\)). ومع ذلك، يتذبذب الموضع y للوسيط، أو دالة الموجة، بين\(+A\) و\(−A\)، ويكرر كل طول موجة\(λ\).
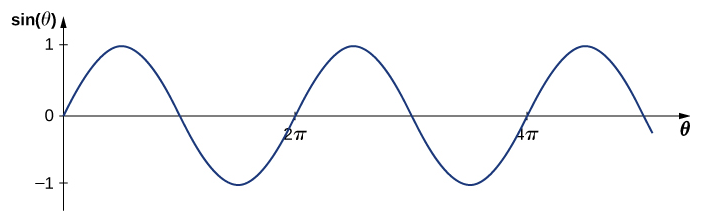
لإنشاء نموذجنا للموجة باستخدام دالة دورية، ضع في اعتبارك نسبة الزاوية والموضع،
\[\begin{align*} \dfrac{\theta}{x} &=\frac{2 \pi}{\lambda}, \\[4pt] \theta &=\frac{2 \pi}{\lambda} x. \end{align*}\]
باستخدام دالة الجيب\(\theta = \frac{2\pi}{\lambda}x\) وضربها بالسعة A، يمكننا الآن تمثيل موضع y للسلسلة كدالة للموضع x:
\[ y(x)=A \sin \left(\frac{2 \pi}{\lambda} x\right). \nonumber \]
تنتقل الموجة الموجودة على الخيط في اتجاه x الموجب بسرعة ثابتة v، وتتحرك لمسافة vt في زمن t. يمكن الآن تحديد وظيفة الموجة من خلال
\[ y(x, t)=A \sin \left(\frac{2 \pi}{\lambda}(x-v t)\right). \nonumber \]
غالبًا ما يكون من الملائم إعادة كتابة وظيفة الموجة هذه في شكل أكثر إحكاما. الضرب في النسبة\(\frac{2\pi}{\lambda}\) يؤدي إلى المعادلة
\[ y(x, t)=A \sin \left(\frac{2 \pi}{\lambda} x-\frac{2 \pi}{\lambda} v t\right). \nonumber \]
\(\frac{2\pi}{\lambda}\)يتم تعريف القيمة على أنها رقم الموجة. رمز رقم الموجة هو k ويحتوي على وحدات العدادات العكسية، m −1:
\[ k \equiv \frac{2 \pi}{\lambda} \label{16.2} \]
تذكر من التذبذبات أن التردد الزاوي يُعرّف بأنه\(\omega \equiv \frac{2\pi}{T}\). يصبح المصطلح الثاني من دالة الموجة
\[\frac{2 \pi}{\lambda} v t=\frac{2 \pi}{\lambda}\left(\frac{\lambda}{T}\right) t=\frac{2 \pi}{T} t=\omega t. \nonumber \]
تنخفض وظيفة الموجة للموجة التوافقية البسيطة على السلسلة إلى
\[ y(x, t)=A \sin (k x \mp \omega t) \nonumber \]
حيث A هو السعة،\(k = \frac{2\pi}{\lambda}\) هو رقم الموجة،\(\omega = \frac{2\pi}{T}\) هو التردد الزاوي، علامة الطرح هي للموجات التي تتحرك في اتجاه x الموجب، وعلامة الجمع هي للموجات التي تتحرك في اتجاه x السلبي. سرعة الموجة تساوي
\[ v=\frac{\lambda}{T}=\frac{\lambda}{T}\left(\frac{2 \pi}{2 \pi}\right)=\frac{\omega}{k} \label{16.3} .\]
فكر مرة أخرى في مناقشتنا للقداس في الربيع، عندما تم تصميم موضع الكتلة على النحو التالي:
\[x(t) = A \cos(ωt+ϕ). \nonumber\]
الزاوية\(ϕ\) عبارة عن تحول طوري، يُضاف للسماح بحقيقة أن الكتلة قد تكون لها ظروف أولية بخلاف\(x = +A\) و\(v = 0\). ولأسباب مماثلة، تتم إضافة المرحلة الأولية إلى وظيفة الموجة. وظيفة الموجة التي تقوم بنمذجة الموجة الجيبية، والتي تسمح بتغيير الطور الأولي\(ϕ\)، هي
\[ y(x, t)=A \sin (k x \mp \omega t+\phi) \label{16.4} \]
القيمة
\[ (k x \mp \omega t+\phi) \label{16.5} \]
تُعرف باسم مرحلة الموجة، حيث\(\phi\) هي المرحلة الأولية من دالة الموجة. يعتمد ما إذا كان المصطلح\(\omega t\) الزمني سلبيًا أو إيجابيًا على اتجاه الموجة. ضع في اعتبارك أولاً علامة الطرح لموجة ذات مرحلة أولية تساوي الصفر (\(\phi\)= 0). ستكون مرحلة الموجة (\(kx = \omega t\)). ضع في اعتبارك اتباع نقطة على الموجة، مثل القمة. ستحدث القمة عندما\(\sin(kx - \omega t = 1.00\)، أي عندما\(k x-\omega t=n \pi+\frac{\pi}{2}\)، لأي قيمة متكاملة لـ n. على سبيل المثال، توجد قمة معينة في\(k x-\omega t=\frac{\pi}{2}\). مع تحرك الموجة، يزداد الوقت ويجب أيضًا زيادة x للحفاظ على المرحلة مساوية لـ\(\frac{\pi}{2}\). لذلك، فإن علامة الطرح هي لموجة تتحرك في اتجاه x الموجب. باستخدام علامة الجمع,\(k x+\omega t=\frac{\pi}{2}\). مع زيادة الوقت، يجب تقليل x للحفاظ على المرحلة مساوية لـ\(\frac{\pi}{2}\). تُستخدم علامة الجمع للموجات التي تتحرك في اتجاه x السلبي. باختصار،\(y(x, t)=A \sin (k x-\omega t+\phi)\) تمثل موجة تتحرك في اتجاه x الموجب\(y(x, t)=A \sin (k x+\omega t+\phi)\) وتمثل موجة تتحرك في اتجاه x السلبي.
تُعرف المعادلة\ ref {16.4} بدالة الموجة التوافقية البسيطة. دالة الموجة هي أي وظيفة من هذا القبيل\(f(x, t)=f(x-v t)\). لاحقًا في هذا الفصل، سنرى أنه حل لمعادلة الموجة الخطية. لاحظ أن هذا\(y(x, t)=A \cos \left(k x+\omega t+\phi^{\prime}\right)\) يعمل بشكل جيد بنفس القدر لأنه يتوافق مع تحول مرحلي مختلف\(\phi^{\prime}=\phi-\frac{\pi}{2}\).
- لإيجاد سعة الموجة الجيبية وطولها الموجي ومدتها وترددها، اكتب دالة الموجة في الشكل\(y(x, t)=A \sin (k x-\omega t+\phi)\).
- يمكن قراءة السعة مباشرة من المعادلة وهي تساوي\(A\).
- يمكن اشتقاق فترة الموجة من التردد الزاوي\( \left(T=\frac{2 \pi}{\omega}\right)\).
- يمكن العثور على التردد باستخدام\(f = \frac{1}{T}\)
- يمكن العثور على الطول الموجي باستخدام رقم الموجة\(\left(\lambda=\frac{2 \pi}{k}\right)\).
تم تصميم الموجة العرضية على سلسلة مشدودة باستخدام وظيفة الموجة
\[ \begin{align*} y(x, t) &=A \sin (k x-w t) \\[4pt] &= (0.2 \: \mathrm{m}) \sin \left(6.28 \: \mathrm{m}^{-1} x-1.57 \: \mathrm{s}^{-1} t\right) \end{align*} \]
أوجد سعة الموجة، وطولها الموجي، ومدتها، وسرعتها.
إستراتيجية
يمكن العثور على كل خصائص الموجة هذه من الثوابت المدرجة في المعادلة أو من مجموعات بسيطة من هذه الثوابت.
الحل
1. يمكن قراءة السعة ورقم الموجة والتردد الزاوي مباشرة من معادلة الموجة:
\ ابدأ {المحاذاة}
(x، t) =& A\ sin (k x-w t) =0.2\:\ الرياضيات {م}\\ الخطيئة\ اليسار (6.28\:\ الرياضيات {م} ^ {-1} x-1.57\:\ الرياضيات {s} ^ {-1} t\ اليمين)\ لا يوجد رقم\
\\\\ يسار (A=0.2\:\ الرياضيات {}} م; k=6.28\:\ الرياضيات {m} ^ {-1};\ أوميغا =1.57\:\ الرياضيات {s} ^ {-1}\ اليمين)\ لا يوجد رقم
\ نهاية {محاذاة}}
2. يمكن استخدام رقم الموجة للعثور على الطول الموجي:
\ ابدأ {المصفوفة} {l}
k=\ frac {2\ pi} {\ lambda}
\\\ لامدا =\ frac {2\ pi} {k} =\ frac {2\ pi} {6.28\:\ ماثرم {م} ^ {-1} =1.0\\ الرياضيات {م}
\ النهاية {المصفوفة}
3. يمكن العثور على فترة الموجة باستخدام التردد الزاوي:
\ ابدأ {المصفوفة} {l}
\ أوميغا =\ frac {2\ pi} {T}\\\
T=\ frac {2\ pi} {\ أوميغا} =\ frac {2\ pi} {1.57\ mathrm {s} ^ {-1}} =4\:\ الرياضيات {s}
\ النهاية {المصفوفة}
4. يمكن العثور على سرعة الموجة باستخدام رقم الموجة والتردد الزاوي. يمكن تحديد اتجاه الموجة من خلال النظر في علامة\(k x \mp \omega t\): تشير العلامة السلبية إلى أن الموجة تتحرك في اتجاه x الإيجابي:
\[ |v|=\frac{\omega}{k}=\frac{1.57 \: \mathrm{s}^{-1}}{6.28 \: \mathrm{m}^{-1}}=0.25 \: \mathrm{m} / \mathrm{s} \nonumber\]
الأهمية
جميع خصائص الموجة موجودة في وظيفة الموجة. لاحظ أن سرعة الموجة هي سرعة الموجة في الاتجاه الموازي لحركة الموجة. يمكن أن يوفر رسم ارتفاع الوسيط y مقابل الموضع x لمرتين t = 0.00 ثانية و t = 0.80 ثانية تصورًا رسوميًا للموجة (الشكل\(\PageIndex{4}\)).
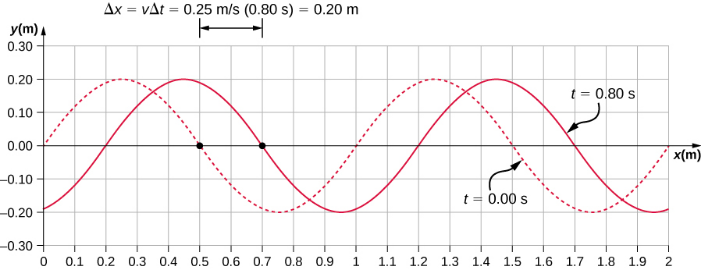
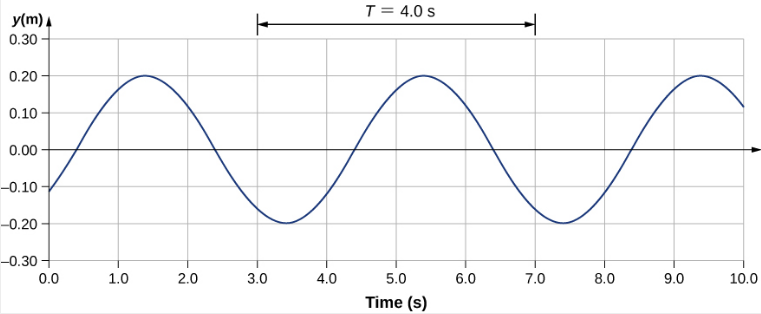
هناك سرعة ثانية للحركة. في هذا المثال، تكون الموجة عرضية وتتحرك أفقيًا بينما يتأرجح الوسيط لأعلى ولأسفل عموديًا على اتجاه الحركة. يوضِّح الرسم البياني في الشكل\(\PageIndex{5}\) حركة الوسيط عند النقطة x = 0.60 m كدالة للوقت. لاحظ أن وسط الموجة يتأرجح لأعلى ولأسفل بين y = +0.20 m و y = −0.20 m في كل فترة من 4.0 ثانية.
يتم اشتقاق دالة الموجة أعلاه باستخدام دالة جيبية. هل يمكن استخدام دالة جيب التمام بدلاً من ذلك؟
سرعة الوسيط وتسارعه
كما هو موضح في المثال\(\PageIndex{2}\)، تكون سرعة الموجة ثابتة وتمثل سرعة الموجة أثناء انتشارها عبر الوسط، وليس سرعة الجسيمات التي تشكل الوسط. تتأرجح جزيئات الوسط حول موضع التوازن بينما تنتشر الموجة عبر الوسط. في حالة انتشار الموجة العرضية في الاتجاه x، تتأرجح الجسيمات لأعلى ولأسفل في الاتجاه y، عموديًا على حركة الموجة. سرعة جزيئات الوسط ليست ثابتة، مما يعني وجود تسارع. يمكن العثور على سرعة الوسيط، المتعامد مع سرعة الموجة في الموجة العرضية، بأخذ المشتق الجزئي لمعادلة الموضع فيما يتعلق بالوقت. يتم العثور على المشتق الجزئي من خلال أخذ مشتق الدالة، ومعالجة جميع المتغيرات كثوابت، باستثناء المتغير المعني. في حالة المشتق الجزئي فيما يتعلق بالوقت\(t\)،\(x\) يتم التعامل مع الموضع على أنه ثابت. على الرغم من أن هذا قد يبدو غريبًا إذا لم تره من قبل، فإن الهدف من هذا التمرين هو إيجاد السرعة العرضية عند نقطة ما، لذلك بهذا المعنى، لا يتغير\(x\) موضع -. لدينا
\[\begin{split} y(x,t) & = A \sin (kx - \omega t + \phi) \\ v_{y} (x,t) & = \frac{\partial y(x,t)}{\partial t} = \frac{\partial}{\partial t} [A \sin (kx - \omega t + \phi)] \\ & = -A \omega \cos (kx - \omega t + \phi) \\ & = -v_{y\; max} \cos (kx - \omega t + \phi) \ldotp \end{split}\]
حجم السرعة القصوى للوسيط هو\(|v_{y\, max}| = A \omega\). قد يبدو هذا مألوفًا من التذبذبات والكتلة في الربيع.
يمكننا إيجاد تسارع الوسط بأخذ المشتق الجزئي لمعادلة السرعة فيما يتعلق بالوقت،
\[\begin{split} a_{y} (x,t) & = \frac{\partial v_{y}(x,t)}{\partial t} = \frac{\partial}{\partial t} [-A \omega \cos (kx - \omega t + \phi)] \\ & = -A \omega^{2} \sin (kx - \omega t + \phi) \\ & = -a_{y\; max} \sin (kx - \omega t + \phi) \ldotp \end{split}\]
حجم التسارع الأقصى هو |a y max | = A\(\omega^{2}\). تتأرجح جزيئات الوسط، أو عناصر الكتلة، بحركة توافقية بسيطة لموجة ميكانيكية.
معادلة الموجة الخطية
لقد حددنا للتو سرعة الوسيط عند الموضع x بأخذ المشتق الجزئي، فيما يتعلق بالوقت، للموضع y. وبالنسبة للموجة العرضية، تكون هذه السرعة متعامدة مع اتجاه انتشار الموجة. وجدنا التسارع بأخذ المشتق الجزئي، فيما يتعلق بالوقت، للسرعة، وهو المشتق للمرة الثانية للموضع:
\[a_{y} (x,t) = \frac{\partial^{2} y(x,t)}{\partial t^{2}} = \frac{\partial^{2}}{\partial t^{2}} [A \sin(kx - \omega t + \phi)] = -A \omega^{2} \sin (kx - \omega t + \phi) \ldotp\]
الآن ضع في اعتبارك المشتقات الجزئية فيما يتعلق بالمتغير الآخر، الموضع x، مع الاحتفاظ بثابت الوقت. المشتق الأول هو منحدر الموجة عند النقطة x في الوقت t،
\[slope = \frac{\partial y(x,t)}{\partial x} = \frac{\partial}{\partial x} [A \sin (kx - \omega t + \phi)] = Ak \cos (kx - \omega t + \phi) \ldotp\]
يعبر المشتق الجزئي الثاني عن كيفية تغير منحدر الموجة فيما يتعلق بالموضع - وبعبارة أخرى، انحناء الموجة، حيث
\[curvature = \frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{\partial^{2}}{\partial x^{2}} [A \sin (kx - \omega t + \phi)] = -Ak^{2} \sin (kx - \omega t + \phi) \ldotp\]
تؤدي نسبة التسارع والانحناء إلى علاقة مهمة جدًا في الفيزياء تُعرف باسم معادلة الموجة الخطية. يؤدي أخذ النسبة واستخدام المعادلة v = إلى\(\frac{\omega}{k}\) الحصول على معادلة الموجة الخطية (المعروفة أيضًا ببساطة باسم معادلة الموجة أو معادلة السلسلة المهتزة)،
\[\begin{split} \frac{\frac{\partial^{2} y(x,t)}{\partial t^{2}}}{\frac{\partial^{2} y(x,t)}{\partial x^{2}}} & = \frac{-A \omega^{2} \sin (kx - \omega t + \phi)}{-Ak^{2} \sin (kx - \omega t + \phi)} \\ & = \frac{\omega^{2}}{k^{2}} = v^{2}, \end{split}\]
\[\frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}} \ldotp \label{16.6}\]
المعادلة\ ref {16.6} هي معادلة الموجة الخطية، وهي واحدة من أهم المعادلات في الفيزياء والهندسة. لقد استخلصناها هنا لموجة عرضية، ولكنها مهمة بنفس القدر عند دراسة الموجات الطولية. تم اشتقاق هذه العلاقة أيضًا باستخدام موجة جيبية، ولكنها تصف بنجاح أي موجة أو نبضة لها الشكل y (x، t) = f (x vt). تنتج هذه الموجات بسبب قوة الاستعادة الخطية للوسيط - وبالتالي، اسم معادلة الموجة الخطية. أي دالة موجة تفي بهذه المعادلة هي دالة موجة خطية.
يتمثل أحد الجوانب المثيرة للاهتمام في معادلة الموجة الخطية في أنه إذا كانت دالتان موجتان عبارة عن حلول فردية لمعادلة الموجة الخطية، فإن مجموع وظيفتي الموجة الخطية يعد أيضًا حلًا لمعادلة الموجة. خذ بعين الاعتبار موجتين عرضيتين تنتشران على طول المحور السيني وتشغلان نفس الوسط. افترض أنه يمكن نمذجة الموجات الفردية باستخدام وظائف الموجة y 1 (x، t) = f (x vt) و y 2 (x، t) = g (x vt)، وهي حلول لمعادلات الموجة الخطية وبالتالي فهي وظائف موجة خطية. مجموع وظائف الموجة هو دالة الموجة
\[y_{1} (x,t) + y_{2} (x,t) = f(x \mp vt) + g(x \mp vt) \ldotp\]
خذ بعين الاعتبار معادلة الموجة الخطية:
\[\begin{split} \frac{\partial^{2} (f + g)}{\partial x^{2}} & = \frac{1}{v^{2}} \frac{\partial^{2} (f + g)}{\partial t^{2}} \\ \frac{\partial^{2} f}{\partial x^{2}} + \frac{\partial^{2} g}{\partial x^{2}} & = \frac{1}{v^{2}} \left(\dfrac{\partial^{2} f}{\partial t^{2}} + \frac{\partial^{2} g}{\partial t^{2}}\right) \ldotp \end{split}\]
أظهر هذا أنه إذا تمت إضافة دالتين للموجة الخطية جبريًا، فإن دالة الموجة الناتجة تكون خطية أيضًا. تمثل وظيفة الموجة هذه إزاحة وسط الموجة الناتجة في كل موضع على طول المحور السيني. إذا احتلت موجتان خطيتان نفس الوسط، فيقال إنهما تتداخلان. إذا كان من الممكن نمذجة هذه الموجات باستخدام دالة الموجة الخطية، فإن وظائف الموجة هذه تضيف لتشكيل معادلة الموجة للموجة الناتجة عن تداخل الموجات الفردية. إن إزاحة الوسط عند كل نقطة من الموجة الناتجة هي المجموع الجبري لعمليات النزوح بسبب الموجات الفردية.
بأخذ هذا التحليل خطوة إلى الأمام، إذا كانت وظائف الموجة y1 (x، t) = f (x vt) و y2 (x، t) = g (x vt) هي حلول لمعادلة الموجة الخطية، فإن Ay 1 (x، t) + بواسطة 2 (x، y)، حيث A و B ثوابت، هي أيضًا حل لمعادلة الموجة الخطية. تُعرف هذه الخاصية بمبدأ التراكب. تمت تغطية التداخل والتراكب بمزيد من التفصيل في تداخل الموجات.
ضع في اعتبارك خيطًا طويلًا جدًا مشدودًا من قبل طالبين، أحدهما في كل طرف. يتذبذب الطالب A نهاية السلسلة مما ينتج موجة على غرار دالة الموجة y 1 (x, t) = A sin (kx −\(\omega\) t) ويقوم الطالب B بتأرجح الوتر الذي ينتج بضعف التردد، ويتحرك في الاتجاه المعاكس. تتحرك كلتا الموجتين بنفس السرعة v =\(\frac{\omega}{k}\). تتداخل الموجتان لتشكيل موجة ناتجة تكون وظيفة الموجة الخاصة بها هي y R (x، t) = y 1 (x، t) + y 2 (x، t). أوجد سرعة الموجة الناتجة باستخدام معادلة الموجة الخطية\(\frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}}\).
إستراتيجية
أولاً، اكتب دالة الموجة للموجة التي أنشأها الطالب الثاني. لاحظ أن التردد الزاوي للموجة الثانية هو ضعف تردد الموجة الأولى (2\(\omega\))، وبما أن سرعة الموجتين هي نفسها، فإن رقم الموجة للموجة الثانية هو ضعف رقم الموجة الأولى (2k). بعد ذلك، اكتب معادلة الموجة لدالة الموجة الناتجة، وهي مجموع داليتي الموجة الفردية. ثم ابحث عن المشتق الجزئي الثاني فيما يتعلق بالموضع والمشتق الجزئي الثاني فيما يتعلق بالوقت. استخدم معادلة الموجة الخطية لإيجاد سرعة الموجة الناتجة.
الحل
- اكتب دالة الموجة للموجة الثانية: y 2 (x، t) = A sin (2kx + 2\(\omega\) t).
- اكتب وظيفة الموجة الناتجة: $y_ {R} (x، t) = y_ {1} (x، t) + y (x، t) = A\ sin (kx -\ أوميغا t) + A\ sin (2kx + 2\ أوميغا t)\ ldotp$$
- ابحث عن المشتقات الجزئية: $$\ ابدأ {تقسيم}\ frac {\ جزئي y_ {R} (x, t)} {\ جزئي x} و = -Ak\ cos (kx -\ أوميغا t) + 2Ak\ cos (2kx + 2\ أوميغا تي)،\\\ frac {\ جزئي ^ {2} y_ {R} (x، t)} {\ جزئي ^ {2}}} & = -Ak^ {2}\ سين (kx -\ أوميغا تي) - 4Ak^ {2}\ سين (2kx + 2\ أوميغا تي)،\\\ frac {\ frac {\ جزئي y_ {R} (x، t)} {\ جزئي t} {\ جزئي} & = -A\ أوميغا\ كوس (kx -\ أوميغا تي) + 2A\ أوميغا\ كوس (2kx + 2\ أوميغا تي)،\\\ فراك {\ جزئي ^ {2} y_ {R} (x، t)} {\ جزئي ^ {2}} و = -A\ أوميغا ^ {2}\ سين (kx -\ أوميغا t) - 4A\ أوميغا ^ {2}\ الخطيئة (2kx + 2\ أوميغا تي)\ ldotp\ end {سبليت} $$
- استخدم معادلة الموجة للعثور على سرعة الموجة الناتجة: $$\ begin {الانقسام}\ frac {\ frac {\\ جزئي ^ {2} y (x, t)} {\\ جزئي x^ {2}} {2} {2}\ frac {\\ جزئي ^ {2} y (x, t)} {\\ t^ {2}},\ -Ak^ {2}\ سين (kx -\ أوميغا تي) + 4Ak^ {2}\ sin (2kx + 2\ أوميغا تي) و =\ frac {1} {v^ {2}}\ يسار (-A\ أوميغا ^ {2}\ sin (kx -\\ left (A\ أوميغا ^ {2}\ sin (kx -\ أوميغا تي) - 4A\ أوميغا ^ {2}\ سين (2kx + 2\ أوميغا تي)\ يمين)،\\ k^ {2}\ يسار (-A\ sin (kx -\ أوميغا t) + 4A\ sin (2kx + 2\ أوميغا تي)\ يمين) و =\ frac {\\ أوميجا ^ {2}} {v^ {2}}\ يسار (A\ sin (kr) x -\ أوميغا تي) - 4A\ sin (2kx + 2\ أوميغا تي)\ يمين)،\\ k^ {2} & =\ frac {\\ أوميغا ^ {2} {v^ {2}}،\\ |v| & =\ frac {\\ أوميغا} {k}\ ldotp\ إنهاء {الانقسام} $$
الأهمية
سرعة الموجة الناتجة تساوي سرعة الموجات الأصلية\(\left(v = \frac{\omega}{k}\right)\). سنبين في القسم التالي أن سرعة الموجة التوافقية البسيطة على الخيط تعتمد على التوتر في الخيط والكتلة لكل طول من السلسلة. لهذا السبب، ليس من المستغرب أن تنتقل الموجات المكونة وكذلك الموجة الناتجة بنفس السرعة.
\(\frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}}\)تعمل معادلة الموجة لأي موجة من النموذج y (x، t) = f (x vt). في القسم السابق، ذكرنا أنه يمكن أيضًا استخدام دالة جيب التمام لنمذجة موجة ميكانيكية متناسقة بسيطة. تحقق مما إذا كانت الموجة
\[y(x,t) = (0.50\; m) \cos (0.20 \pi\; m^{-1} x - 4.00 \pi s^{-1} t + \frac{\pi}{10})\]
هو حل لمعادلة الموجة.
يمكن لأي اضطراب يتوافق مع معادلة الموجة أن ينتشر كموجة تتحرك على طول المحور السيني بسرعة موجة v. إنه يعمل بشكل جيد أيضًا للموجات على السلسلة والموجات الصوتية والموجات الكهرومغناطيسية. هذه المعادلة مفيدة للغاية. على سبيل المثال، يمكن استخدامه لإظهار أن الموجات الكهرومغناطيسية تتحرك بسرعة الضوء.


