Skip to main content
Global

16.2: موجات السفر

  1. Last updated
  2. Save as PDF
  • Page ID
    199855

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم
    • وصف الخصائص الأساسية لحركة الموجة
    • حدد مصطلحات الطول الموجي والسعة والفترة والتردد وسرعة الموجة
    • اشرح الفرق بين الموجات الطولية والعرضية، وقدم أمثلة لكل نوع
    • ضع قائمة بأنواع مختلفة من الموجات

    لقد رأينا في التذبذبات أن الحركة التذبذبية هي نوع مهم من السلوك يمكن استخدامه لنمذجة مجموعة واسعة من الظواهر الفيزيائية. الحركة التذبذبية مهمة أيضًا لأن التذبذبات يمكن أن تولد موجات ذات أهمية أساسية في الفيزياء. تنطبق العديد من المصطلحات والمعادلات التي درسناها في الفصل الخاص بالذبذبات جيدًا بنفس القدر على حركة الموجة (الشكل\(\PageIndex{1}\)).

    صورة لموجة المحيط.
    الشكل\(\PageIndex{1}\): ربما تكون موجة المحيط هي الصورة الأولى التي تتبادر إلى الذهن عندما تسمع كلمة «موجة». على الرغم من أن موجة الانهيار هذه، وموجات المحيط بشكل عام، لها أوجه تشابه واضحة مع خصائص الموجة الأساسية التي سنناقشها، إلا أن الآليات التي تقود موجات المحيط معقدة للغاية وخارج نطاق هذا الفصل. قد يبدو من الطبيعي، بل والمفيد، تطبيق المفاهيم الواردة في هذا الفصل على موجات المحيط، لكن موجات المحيط غير خطية، والنماذج البسيطة المقدمة في هذا الفصل لا تفسرها بالكامل. (تصوير: ستيف جورفيتسون)

    أنواع الموجات

    الموجة هي اضطراب ينتشر أو ينتقل من المكان الذي تم إنشاؤه فيه. هناك ثلاثة أنواع أساسية من الموجات: الموجات الميكانيكية والموجات الكهرومغناطيسية وموجات المادة.

    تخضع الموجات الميكانيكية الأساسية لقوانين نيوتن وتتطلب وسيطًا. الوسيط هو المادة التي تنتشر من خلالها الموجات الميكانيكية، وينتج الوسيط قوة استعادة مرنة عندما يتم تشويهه. تنقل الموجات الميكانيكية الطاقة والزخم، دون نقل الكتلة. بعض الأمثلة على الموجات الميكانيكية هي موجات الماء والموجات الصوتية والموجات الزلزالية. وسيلة الموجات المائية هي الماء؛ أما بالنسبة للموجات الصوتية، فعادة ما تكون الوسيلة هي الهواء. (يمكن أن تنتقل الموجات الصوتية في وسائط أخرى أيضًا؛ سننظر في ذلك بمزيد من التفصيل في الصوت.) بالنسبة لموجات المياه السطحية، يحدث الاضطراب على سطح الماء، ربما بسبب صخرة يتم إلقاؤها في بركة أو عن طريق سباح يرش السطح بشكل متكرر. بالنسبة للموجات الصوتية، فإن الاضطراب هو تغيير في ضغط الهواء، ربما ناتج عن المخروط المتذبذب داخل مكبر الصوت أو شوكة الضبط الاهتزازية. في كلتا الحالتين، يكون الاضطراب هو تذبذب جزيئات السائل. في الموجات الميكانيكية، تنتقل الطاقة والزخم مع حركة الموجة، بينما تتأرجح الكتلة حول نقطة توازن. (نناقش هذا في الطاقة وقوة الموجة.) تولد الزلازل موجات زلزالية من عدة أنواع من الاضطرابات، بما في ذلك اضطراب سطح الأرض واضطرابات الضغط تحت السطح. تنتقل الموجات الزلزالية عبر المواد الصلبة والسوائل التي تشكل الأرض. في هذا الفصل، نركز على الموجات الميكانيكية.

    ترتبط الموجات الكهرومغناطيسية بالتذبذبات في المجالات الكهربائية والمغناطيسية ولا تتطلب وسيطًا. تشمل الأمثلة أشعة جاما والأشعة السينية والموجات فوق البنفسجية والضوء المرئي وموجات الأشعة تحت الحمراء والميكروويف وموجات الراديو. يمكن للموجات الكهرومغناطيسية أن تنتقل عبر الفراغ بسرعة الضوء، v = c = 2.99792458 x 10 8 m/s، على سبيل المثال، ينتقل الضوء من النجوم البعيدة عبر فراغ الفضاء ويصل إلى الأرض. تتميز الموجات الكهرومغناطيسية ببعض الخصائص التي تشبه الموجات الميكانيكية؛ يتم تغطيتها بمزيد من التفصيل في الموجات الكهرومغناطيسية.

    تعد موجات المادة جزءًا أساسيًا من فرع الفيزياء المعروف باسم ميكانيكا الكم. ترتبط هذه الموجات بالبروتونات والإلكترونات والنيوترونات والجسيمات الأساسية الأخرى الموجودة في الطبيعة. تم اقتراح النظرية القائلة بأن جميع أنواع المواد لها خصائص موجية لأول مرة من قبل لويس دي بروغلي في عام 1924. تتم مناقشة موجات المادة في الفوتونات وموجات المادة.

    موجات ميكانيكية

    تُظهر الموجات الميكانيكية الخصائص المشتركة لجميع الموجات، مثل السعة والطول الموجي والفترة والتردد والطاقة. يمكن وصف جميع خصائص الموجة من خلال مجموعة صغيرة من المبادئ الأساسية.

    تتكرر أبسط الموجات الميكانيكية لعدة دورات وترتبط بالحركة التوافقية البسيطة. يمكن تصميم هذه الموجات التوافقية البسيطة باستخدام مزيج من وظائف الجيب وجيب التمام. على سبيل المثال، ضع في اعتبارك موجة المياه السطحية المبسطة التي تتحرك عبر سطح الماء كما هو موضح في الشكل\(\PageIndex{2}\). على عكس موجات المحيط المعقدة، في موجات المياه السطحية، يتحرك الوسط، في هذه الحالة الماء، عموديًا، ويتأرجح لأعلى ولأسفل، بينما يتحرك اضطراب الموجة أفقيًا عبر الوسط. في الشكل\(\PageIndex{2}\)، تتسبب الموجات في تحرك طائر النورس لأعلى ولأسفل بحركة توافقية بسيطة أثناء مرور قمم وأحواض الموجة (القمم والوديان) تحت الطائر. القمة هي أعلى نقطة في الموجة، والحوض هو الجزء السفلي من الموجة. وقت التذبذب الكامل للحركة الصاعدة والهابطة هو فترة الموجة T. تردد الموجة هو عدد الموجات التي تمر عبر نقطة لكل وحدة زمنية ويساوي f =\(\frac{1}{T}\). يمكن التعبير عن الفترة باستخدام أي وحدة زمنية مناسبة ولكن يتم قياسها عادةً بالثواني؛ ويقاس التردد عادةً بالهيرتز (هرتز)، حيث 1 هرتز = 1 ثانية −1.

    يُطلق على طول الموجة اسم الطول الموجي ويتم تمثيله بالحرف اليوناني lambda (\(\lambda\))، والذي يتم قياسه بأي وحدة طول ملائمة، مثل السنتيمتر أو المتر. يمكن قياس الطول الموجي بين أي نقطتين متشابهتين على طول الوسط لهما نفس الارتفاع ونفس المنحدر. في الشكل\(\PageIndex{2}\)، يظهر الطول الموجي مقاسًا بين قمتين. كما هو مذكور أعلاه، فإن فترة الموجة تساوي وقت التذبذب الواحد، ولكنها تساوي أيضًا الوقت الذي يمر فيه طول موجة واحدة عبر نقطة على طول مسار الموجة.

    سعة الموجة (A) هي مقياس الحد الأقصى لإزاحة الوسيط من موضع توازنه. في الشكل، يُشار إلى موضع التوازن بالخط المنقط، وهو ارتفاع الماء إذا لم تكن هناك موجات تتحرك عبره. في هذه الحالة، تكون الموجة متماثلة، وقمة الموجة هي مسافة +A فوق موضع التوازن، ويكون الحوض الصغير مسافة −A تحت موضع التوازن. يمكن أن تكون وحدات السعة بالسنتيمتر أو الأمتار، أو أي وحدة مسافة ملائمة.

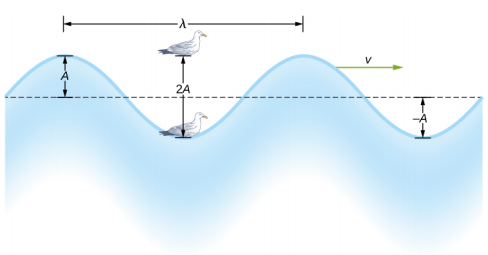
    يوضح الشكل موجة بموضع التوازن المحدد بخط أفقي. تُسمى المسافة الرأسية من الخط إلى قمة الموجة x وتلك المسافة من الخط إلى الحوض ناقص x، ويظهر طائر يتحرك صعودًا وهبوطًا في الموجة. يتم تصنيف المسافة الرأسية التي يقطعها الطائر 2x. يُطلق على المسافة الأفقية بين قمتين متتاليتين اسم lambda. يُطلق على المتجه الذي يشير إلى اليمين اسم v subcript w.
    الشكل\(\PageIndex{2}\): تمر موجة مياه سطحية مثالية تحت طائر النورس الذي يتحرك صعودًا وهبوطًا بحركة توافقية بسيطة. للموجة طول الموجي\(\lambda\)، وهو المسافة بين الأجزاء المتطابقة المتجاورة من الموجة. السعة A للموجة هي الحد الأقصى لإزاحة الموجة من موضع التوازن، والذي يشار إليه بالخط المنقط. في هذا المثال، يتحرك الوسيط لأعلى ولأسفل، بينما ينتشر اضطراب السطح بالتوازي مع السطح بسرعة v.

    تتحرك موجة الماء في الشكل عبر الوسط بسرعة انتشار\(\vec{v}\). حجم سرعة الموجة هو المسافة التي تقطعها الموجة في وقت معين، وهو طول موجة واحد في وقت فترة واحدة، وسرعة الموجة هي حجم سرعة الموجة. في شكل المعادلة، هذا هو

    \[v = \frac{\lambda}{T} = \lambda f \ldotp \label{16.1}\]

    تنطبق هذه العلاقة الأساسية على جميع أنواع الموجات. بالنسبة لموجات الماء، v هي سرعة الموجة السطحية؛ بالنسبة للصوت، v هي سرعة الصوت؛ وبالنسبة للضوء المرئي، v هي سرعة الضوء.

    الموجات العرضية والطولية

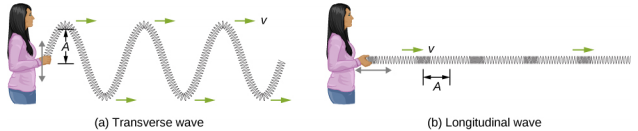
    لقد رأينا أن الموجة الميكانيكية البسيطة تتكون من اضطراب دوري ينتشر من مكان إلى آخر عبر وسيط. في الشكل\(\PageIndex{3}\) (أ)، تنتشر الموجة في الاتجاه الأفقي، بينما يتم إزعاج الوسط في الاتجاه الرأسي. هذه الموجة تسمى الموجة العرضية. في الموجة العرضية، قد تنتشر الموجة في أي اتجاه، ولكن اضطراب الوسط يكون عموديًا على اتجاه الانتشار. في المقابل، في الموجة الطولية أو الموجة الانضغاطية، يكون الاضطراب موازيًا لاتجاه الانتشار. يوضح الشكل\(\PageIndex{3}\) (ب) مثالاً للموجة الطولية. حجم الاضطراب هو اتساعه A وهو مستقل تمامًا عن سرعة الانتشار v.

    يُظهر الشكل أ، المسمى الموجة العرضية، شخصًا يمسك بأحد طرفي زنبرك طويل تم وضعه أفقيًا ويحركه لأعلى ولأسفل. يشكل الربيع موجة تنتشر بعيدًا عن الشخص. هذه تسمى الموجة العرضية. تُسمى المسافة الرأسية بين قمة الموجة وموضع توازن الزنبرك A. يوضح الشكل (ب)، المسمى «الموجة الطولية»، الشخص الذي يحرك الزنبرك من وإلى أفقياً. يتم ضغط الزنبرك وتمديده بالتناوب. هذه تسمى الموجة الطولية. تُسمى المسافة الأفقية من منتصف ضغط واحد إلى منتصف فتحة واحدة بـ A.
    الشكل\(\PageIndex{3}\): (أ) في الموجة العرضية، يتأرجح الوسط عموديًا على سرعة الموجة. هنا، يتحرك الزنبرك عموديًا لأعلى ولأسفل، بينما تنتشر الموجة أفقيًا إلى اليمين. (ب) في الموجة الطولية، يتذبذب الوسط بالتوازي مع انتشار الموجة. في هذه الحالة، يتأرجح الربيع ذهابًا وإيابًا، بينما تنتشر الموجة إلى اليمين.

    يظهر في الشكل تمثيل رسومي بسيط لقسم من الزنبرك الموضح في الشكل\(\PageIndex{3}\) (ب)\(\PageIndex{4}\). يوضح الشكل\(\PageIndex{4}\) (أ) موضع توازن الزنبرك قبل أن تتحرك أي موجات لأسفل. يتم تمييز نقطة في الربيع بنقطة زرقاء. يُظهر الشكل\(\PageIndex{4}\) (ب) حتى (ز) لقطات للربيع مأخوذة بفارق ربع فترة عن بعضها البعض، وفي بعض الأحيان بعد نهاية النبع يتذبذب ذهابًا وإيابًا في الاتجاه السيني بتردد ثابت. يُنظر إلى اضطراب الموجة على أنه ضغط وتوسعات الربيع. لاحظ أن النقطة الزرقاء تتأرجح حول موضع الاتزان على مسافة A، بينما تتحرك الموجة الطولية في اتجاه x الموجب بسرعة ثابتة. المسافة A هي سعة الموجة. لا يتغير الموضع y للنقطة مع تحرك الموجة خلال الربيع. يتم قياس الطول الموجي للموجة في الجزء (د). يعتمد الطول الموجي على سرعة الموجة وتردد القوة الدافعة.

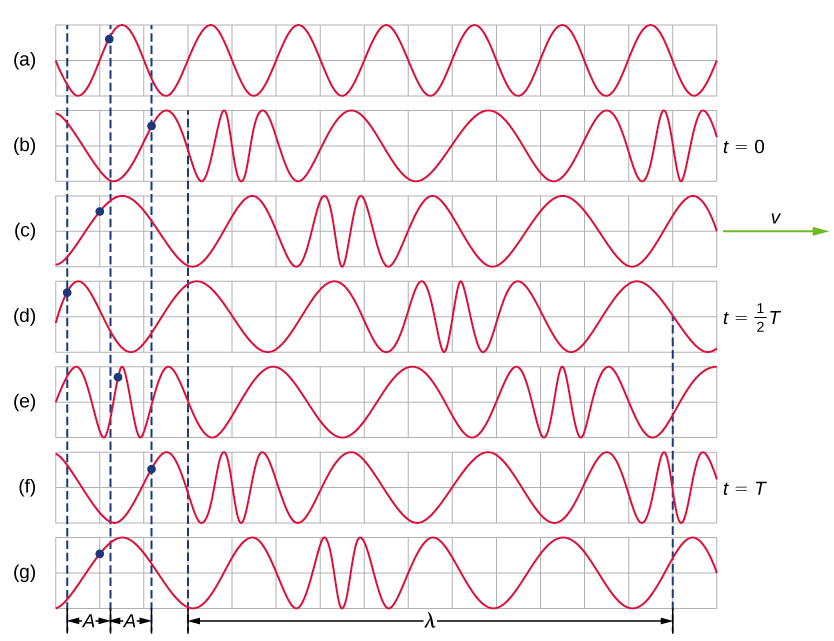
    تُظهر الأشكال من الألف إلى الياء مراحل مختلفة من الموجة الطولية التي تمر عبر الربيع. تشير النقطة الزرقاء إلى نقطة في الربيع. ينتقل هذا من اليسار إلى اليمين بينما تنتشر الموجة نحو اليمين. في الشكل b في الوقت t=0، تكون النقطة على يمين موضع التوازن. في الشكل d، في الوقت الذي يساوي نصف T، تكون النقطة على يسار موضع التوازن. في الشكل f، في الوقت t=t، تظهر النقطة مرة أخرى إلى اليمين. المسافة بين موضع التوازن والموضع الأقصى الأيسر أو الأيمن للنقطة هي نفسها وتسمى A. المسافة بين جزأين متطابقين من الموجة تسمى lambda.

    الشكل\(\PageIndex{4}\): (أ) هذا تمثيل رسومي بسيط لقسم من الزنبرك الممتد الموضح في الشكل\(\PageIndex{3}\) (ب)، ويمثل موضع توازن الزنبرك قبل حدوث أي موجات في الزنبرك. يتم تمييز نقطة في الربيع بنقطة زرقاء. (b—g) يتم إنشاء الموجات الطولية عن طريق تذبذب نهاية الربيع (غير موضح) ذهابًا وإيابًا على طول المحور السيني. تتحرك الموجة الطولية، ذات الطول الموجي\(\lambda\)، على طول الزنبرك في اتجاه +x بسرعة موجة v. للراحة، يتم قياس الطول الموجي بـ (d). لاحظ أن النقطة الموجودة على الزنبرك التي تم تمييزها بالنقطة الزرقاء تتحرك ذهابًا وإيابًا على مسافة A من موضع التوازن، وتتأرجح حول موضع توازن النقطة.

    قد تكون الموجات عرضية أو طولية أو مزيجًا من الاثنين. ومن أمثلة الموجات العرضية الموجات على الآلات الوترية أو الموجات السطحية على الماء، مثل التموجات المتحركة على البركة. الموجات الصوتية في الهواء والماء طولية. في الموجات الصوتية، تكون الاضطرابات عبارة عن تغيرات دورية في الضغط تنتقل في السوائل. لا تتمتع السوائل بقوة قص ملحوظة، ولهذا السبب فإن الموجات الصوتية فيها هي موجات طولية. يمكن أن يحتوي الصوت في المواد الصلبة على مكونات طولية وعرضية، مثل تلك الموجودة في الموجة الزلزالية. تولد الزلازل موجات زلزالية تحت سطح الأرض بمكونات طولية وعرضية (تسمى الموجات الانضغاطية أو الموجات P وموجات القص أو الموجات S، على التوالي). تتميز مكونات الموجات الزلزالية بخصائص فردية مهمة - فهي تنتشر بسرعات مختلفة، على سبيل المثال. تحتوي الزلازل أيضًا على موجات سطحية تشبه الموجات السطحية على الماء. تحتوي موجات المحيط أيضًا على مكونات عرضية وطولية.

    مثال 16.1: موجة على سلسلة

    يأخذ الطالب خيطًا طوله 30.00 مترًا ويربط أحد طرفيه بالحائط في مختبر الفيزياء. يقوم الطالب بعد ذلك بإمساك الطرف الحر للحبل، مع الحفاظ على ثبات الشد في الحبل. يبدأ الطالب بعد ذلك في إرسال الموجات إلى أسفل الخيط عن طريق تحريك نهاية الخيط لأعلى ولأسفل بتردد 2.00 هرتز. الحد الأقصى لإزاحة نهاية السلسلة هو 20.00 سم. تصطدم الموجة الأولى بجدار المختبر بعد 6.00 ثانية من إنشائه. (أ) ما هي سرعة الموجة؟ (ب) ما هي فترة الموجة؟ (ج) ما الطول الموجي للموجة؟

    إستراتيجية

    1. يمكن اشتقاق سرعة الموجة بقسمة المسافة المقطوعة على الوقت.
    2. فترة الموجة هي عكس تردد القوة الدافعة.
    3. يمكن العثور على الطول الموجي من السرعة والفترة v =\(\frac{\lambda}{T}\).
    الحل
    1. قطعت الموجة الأولى مسافة 30.00 مترًا في 6.00 ثانية: $v =\ frac {30.00\; m} {6.00\; s} = 5.00\; م/ث\ ldotp$$
    2. . الفترة تساوي معكوس التردد: $T =\ frac {1} {f} =\ frac {1} {2.00\; s^ {-1}} = 0.50\; s\ ldotp$$
    3. الطول الموجي يساوي السرعة مضروبة في الفترة: $$\ lambda = vT = (5.00\; م/ث) (0.50\; s) = 2.50\; m\ ldotp$$

    الدلالة

    إن تردد الموجة الناتجة عن قوة دافعة متذبذبة يساوي تردد القوة الدافعة.

    التمرين 16.1

    g عندما يتم انتزاع أوتار الجيتار، تتأرجح سلسلة الجيتار نتيجة تحرك الموجات عبر الوتر. تتسبب اهتزازات الخيط في تذبذب جزيئات الهواء وتشكيل موجات صوتية. تردد الموجات الصوتية يساوي تردد السلسلة المهتزة. هل الطول الموجي للموجة الصوتية يساوي دائمًا الطول الموجي للموجات على الوتر؟

    مثال 16.2: خصائص الموجة

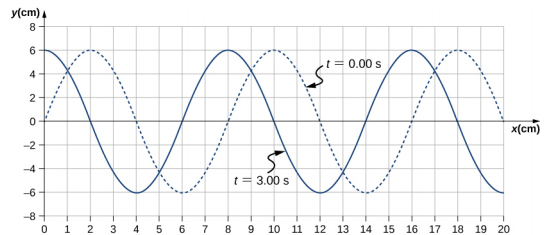
    تنتشر موجة ميكانيكية عرضية في الاتجاه السيني الموجب عبر زنبرك (كما هو موضح في الشكل\(\PageIndex{3}\) (أ)) بسرعة موجة ثابتة، ويتأرجح الوسط بين +A و −A حول موضع توازن. \(\PageIndex{5}\)يوضح الرسم البياني في الشكل ارتفاع الزنبرك (y) مقابل الموضع (x)، حيث يشير المحور x في اتجاه الانتشار. يوضِّح الشكل ارتفاع الزنبرك مقابل الموضع x عند t = 0.00 ثانية كخط منقط والموجة عند t = 3.00 s كخط صلب. (أ) تحديد الطول الموجي للموجة وسعتها. (ب) أوجد سرعة انتشار الموجة. (ج) احسب فترة الموجة ووتيرتها.

    يوضح الشكل موجتين عرضتين تتراوح قيمتهما y من -6 سم إلى 6 سم. تظهر موجة واحدة، تحمل علامة t = 0 ثانية كخط منقط. لها قمم عند x تساوي 2 و 10 و 18 سم. تظهر الموجة الأخرى، التي تحمل علامة t = 3 ثوانٍ كخط صلب. لها قمم عند x تساوي 0 و 8 و 16 سم.
    الشكل\(\PageIndex{5}\): موجة عرضية تظهر في لحظتين من الزمن.

    إستراتيجية

    1. يمكن تحديد السعة والطول الموجي من الرسم البياني.
    2. نظرًا لأن السرعة ثابتة، يمكن العثور على سرعة الموجة بقسمة المسافة التي تقطعها الموجة على الوقت الذي استغرقته الموجة لقطع المسافة.
    3. يمكن العثور على الفترة من v =\(\frac{\lambda}{T}\) والتردد من f =\(\frac{1}{T}\).
    الحل
    1. اقرأ الطول الموجي من الرسم البياني، بالنظر إلى السهم الأرجواني في الشكل\(\PageIndex{6}\). اقرأ السعة من خلال النظر إلى السهم الأخضر. الطول الموجي\(\lambda\) = 8.00 سم والسعة هي A = 6.00 cm.
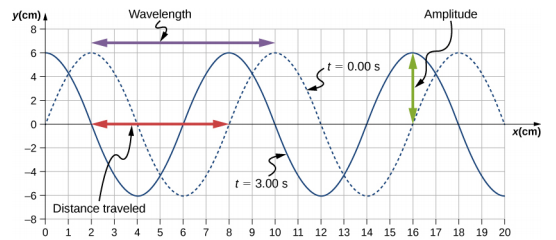
    يوضح الشكل موجتين عرضتين تتراوح قيمتهما y من -6 سم إلى 6 سم. تظهر موجة واحدة، تحمل علامة t = 0 ثانية كخط منقط. لها قمم عند x تساوي 2 و 10 و 18 سم. تظهر الموجة الأخرى، التي تحمل علامة t = 3 ثوانٍ كخط صلب. لها قمم عند x تساوي 0 و 8 و 16 سم. تُسمى المسافة الأفقية بين قمتين متتاليتين الطول الموجي. هذا من x=2 سم إلى x=10 سم. تُسمى المسافة الرأسية من موضع التوازن إلى القمة بالسعة. هذا من y=0 سم إلى y=6 سم. يُطلق على السهم الأحمر اسم المسافة المقطوعة. هذا من x=2 سم إلى x=8 سم.
    الشكل\(\PageIndex{6}\): خصائص الموجة المحددة على الرسم البياني لإزاحتها.
    1. يمكن رؤية المسافة التي قطعتها الموجة من الوقت t = 0.00 ثانية إلى الوقت t = 3.00 ثانية في الرسم البياني. ضع في اعتبارك السهم الأحمر الذي يوضح المسافة التي قطعتها القمة خلال 3 ثوانٍ، والمسافة هي 8.00 سم − 2.00 سم = 6.00 سم. السرعة هي $v =\ frac {\ دلتا x} {\ دلتا تي} =\ فراك {8.00\; سم - 2.00\; سم} {3.00\; s - 0.00\; s} = 2.00\; سم/ثانية\ ldotp$$
    2. الفترة هي T =\(\frac{\lambda}{v}\) =\(\frac{8.00\; cm}{2.00\; cm/s}\) = 4.00\; s والتردد هو f =\(\frac{1}{T}\) =\(\frac{1}{4.00\; s}\) = 0.25 هرتز.

    الدلالة

    لاحظ أنه يمكن العثور على الطول الموجي باستخدام أي نقطتين متطابقتين متتاليتين تتكرران، ويكون لهما نفس الارتفاع والانحدار. يجب عليك اختيار نقطتين أكثر ملاءمة. يمكن أيضًا العثور على الإزاحة باستخدام أي نقطة ملائمة.

    التمرين 16.2

    قد تكون سرعة انتشار الموجة الميكانيكية العرضية أو الطولية ثابتة مع تحرك اضطراب الموجة عبر الوسط. خذ بعين الاعتبار الموجة الميكانيكية العرضية: هل سرعة الوسط ثابتة أيضًا؟