15E: التذبذبات (التمارين)

Last updated
Save as PDF

Page ID: 200108

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

مشاكل

15.1 حركة توافقية بسيطة

أثبت أن استخدام x (t) = Asin ($\omega$t +$\phi$) سيؤدي إلى نفس النتائج للفترة لتذبذبات الكتلة والربيع. لماذا تعتقد أنه تم اختيار دالة جيب التمام؟
ما الفترة التي تبلغ ٦٠٫٠ هرتز من الطاقة الكهربائية؟
إذا كان معدل ضربات قلبك 150 نبضة في الدقيقة أثناء ممارسة التمارين الشاقة، فما الوقت لكل نبضة بوحدات الثواني؟
أوجد تردُّد شوكة رنانة تستغرق ٢٫٥٠ × ١٠ ^−٣ ث لإكمال ذبذبة واحدة.
يتم ضبط ستروبوسكوب ليومض كل ٨٫٠٠ × ١٠ ^−٥ ث. ما تردد الومضات؟
يحتوي الإطار على نمط مداس مع شق كل 2.00 سم. يُحدث كل شق اهتزازًا واحدًا أثناء تحرك الإطار. ما تردد هذه الاهتزازات إذا تحركت السيارة بسرعة ٣٠٫٠ م/ث؟
كل مكبس في المحرك يصدر صوتًا حادًا في كل ثورة أخرى للمحرك. (أ) ما السرعة التي تسير بها سيارة السباق إذا كان محركها ذو الثماني أسطوانات يصدر صوتًا بتردد 750 هرتز، بالنظر إلى أن المحرك يصدر 2000 دورة في الكيلومتر؟ (ب) كم عدد الدورات في الدقيقة التي يدور بها المحرك؟
نوع من ساعات الوقواق يحافظ على الوقت من خلال ارتداد الكتلة على الزنبرك، وعادة ما يكون شيئًا لطيفًا مثل الكروب على الكرسي. ما ثابت القوة اللازم لإنتاج فترة مقدارها 0.500 ثانية لكتلة مقدارها 0.0150 كجم؟
كتلة m ₀ متصلة بنابض وتُعلَّق رأسيًّا. يتم رفع الكتلة لمسافة قصيرة في الاتجاه الرأسي ويتم تحريرها. تتأرجح الكتلة بتردد ₀. إذا استُبدلت الكتلة بكتلة أكبر بتسعة أضعاف، وكُررت التجربة، فما تكرار التذبذبات بدلالة f ₀؟
تتأرجح كتلة مقدارها 0.500 كجم مُعلَّقة من زنبرك بمدة 1.50 ثانية. ما مقدار الكتلة التي يجب إضافتها إلى الجسم لتغيير الفترة إلى 2.00 ثانية؟
ما مقدار الفسحة (النسبة المئوية والكتلة) المتاحة لك في اختيار كتلة الكائن في المشكلة السابقة إذا كنت لا ترغب في أن تكون الفترة الجديدة أكبر من 2.01 ثانية أو أقل من 1.99 ثانية؟

15.2 الطاقة في الحركة التوافقية البسيطة

يتم تعليق الأسماك على مقياس زنبركي لتحديد كتلتها. (أ) ما ثابت قوة الزنبرك في مثل هذا المقياس إذا كان الزنبرك ممتدًا بمقدار ٨٫٠٠ سم لحمولة مقدارها ١٠,٠ كجم؟ (ب) ما كتلة السمكة التي تُمدِّد النبع بمقدار 5.50 سم؟ (ج) ما مدى تباعد علامات نصف الكيلوغرام على الميزان؟
حان الوقت المناسب لفريق الرجبي المحلي الذي يقل وزنه عن 85 كجم. يمكن وصف مقياس الحمام المستخدم لتقييم الأهلية بموجب قانون Hooke ويتم خفضه بمقدار 0.75 سم بحمولته القصوى البالغة 120 كجم. (أ) ما هو ثابت القوة الفعالة للزنبرك؟ (ب) يقف اللاعب على الميزان ويخفضه بمقدار 0.48 سم. هل هو مؤهل للعب في هذا الفريق تحت 85 كجم؟
يستخدم أحد أنواع مسدسات BB غطاسًا يحركه زنبرك لتفجير BB من البرميل. (أ) احسب ثابت قوة زنبرك المكبس إذا كان عليك ضغطه بمقدار 0.150 مترًا لدفع المكبس الذي يبلغ وزنه 0.0500 كجم إلى سرعة قصوى تبلغ 20.0 م/ث. (ب) ما القوة التي يجب القيام بها لضغط الزنبرك؟
عندما يقف رجل وزنه ٨٠٫٠ كجم على عصا بوجو، يتم ضغط الزنبرك بمقدار ٠٫١٢٠ م. (أ) ما ثابت قوة الزنبرك؟ (ب) هل سيضغط الزنبرك أكثر عندما يقفز على الطريق؟
يبلغ طول الزنبرك ٠٫٢٠٠ م عندما تتدلى منه كتلة مقدارها ٠٫٣٠٠ كجم، وطوله ٠٫٧٥٠ مترًا عندما تتدلى منه كتلة وزنها ١٫٩٥ كجم. (أ) ما هو ثابت قوة الزنبرك؟ (ب) ما طول الزنبرك الذي لم يتم تفريغه؟
يبلغ ثابت القوة الفعالة لطول حبل النايلون الذي يُعلق منه متسلق الجبال 1.40 × 10 ⁴ نيوتن/م. (أ) ما التردد الذي يرتد عنده، إذا كانت كتلته زائدًا وكتلة معداته ٩٠٫٠ كجم؟ (ب) إلى أي مدى يمكن أن يمتد هذا الحبل لكسر سقوط المتسلق إذا سقط لمسافة 2.00 متر قبل نفاد الحبل من الركود؟ (تلميح: استخدم الحفاظ على الطاقة.) (ج) كرر كلا الجزئين من هذه المشكلة في حالة استخدام ضعف هذا الطول من حبل النايلون.

15.3 مقارنة الحركة التوافقية البسيطة والحركة الدائرية

يمكن أيضًا تصميم حركة الكتلة على الزنبرك المعلق عموديًا، حيث تتأرجح الكتلة لأعلى ولأسفل، باستخدام القرص الدوار. بدلاً من وضع الأضواء أفقيًا على طول الجزء العلوي والإشارة لأسفل، ضع الأضواء عموديًا واجعل الأضواء تلمع على جانب القرص الدوار. سيتم إنتاج ظل على جدار قريب، وسوف يتحرك لأعلى ولأسفل. اكتب معادلات الحركة للظل مع أخذ الموضع عند t = 0.0 s ليكون y = 0.0 m مع تحرك الكتلة في الاتجاه y الموجب.
(أ) ساعة جديدة لها جسم كتلته 0.0100 كجم وهو يرتد على زنبرك ثابت قوته 1.25 نيوتن لكل متر، فما أقصى سرعة للجسم إذا ارتد الجسم بمقدار 3.00 سم فوق موضع الاتزان وتحته؟ (ب) ما عدد الجولات من طاقة الحركة التي يمتلكها الجسم عند سرعته القصوى؟
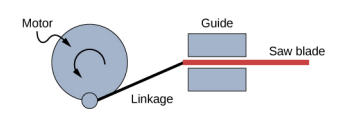
تستخدم الحركة الترددية دوران المحرك لإنتاج حركة خطية لأعلى ولأسفل أو ذهابًا وإيابًا. هذه هي الطريقة التي يعمل بها المنشار الترددي، كما هو موضح أدناه. إذا كان المحرك يدور بسرعة 60 هرتز وكان نصف قطره 3.0 سم، فقم بتقدير السرعة القصوى لشفرة المنشار أثناء تحركها لأعلى ولأسفل. يُعرف هذا التصميم باسم نير سكوتش.

رسم تخطيطي لمحرك، تم تصويره على هيئة قرص يدور على محوره، مما يتسبب في تحرك شفرة المنشار أفقيًا. يوجد في الجزء السفلي من قرص المحرك رابط يتصل بالنصل الأفقي. يمكن أن يتمحور الارتباط عند كلا الطرفين. يتم تقييد النصل للتحرك أفقيًا من خلال فجوة أفقية في كتلة التوجيه.

يقف طالب على حافة جولة مرح تدور خمس مرات في الدقيقة ويبلغ نصف قطرها مترين في إحدى الأمسيات مع غروب الشمس. ينتج الطالب ظلًا على المبنى المجاور. (أ) اكتب معادلة لموضع الظل. (ب) اكتب معادلة لسرعة الظل.

15.4 البندول

ما طول البندول الذي تبلغ مدته 0.500 ثانية؟
يعتقد بعض الناس أن البندول الذي تبلغ مدته 1.00 ثانية يمكن تشغيله «بالطاقة العقلية» أو الحركية النفسية، لأن فترته هي نفس متوسط ضربات القلب. صحيح أم لا، ما هو طول هذا البندول؟
ما فترة البندول الذي يبلغ طوله ١٫٠٠ م؟
ما المدة التي تستغرقها طفلة على الأرجوحة لإكمال أرجوحة واحدة إذا كان مركز جاذبيتها يقع على مسافة ٤٫٠٠ م تحت المحور؟
يبلغ طول البندول الموجود على ساعة الوقواق 5.00 سم. ما تردده؟
يجلس اثنان من الببغاوات على أرجوحة مع CMs المدمجة الخاصة بهم على ارتفاع 10.0 سم تحت المحور. في أي تردد يتأرجحون؟
(أ) البندول الذي تبلغ مدته 3.00000 ثانية والذي يقع حيث تبلغ التسارع الناتج عن الجاذبية 9.79 متر/ثانية ^{2 يُنقل} إلى موقع تبلغ فيه التسارع الناتج عن الجاذبية 9.82 متر/ثانية ². ما هي فترتها الجديدة؟ (ب) شرح سبب الحاجة إلى هذا العدد الكبير من الأرقام في قيمة الفترة، استنادا إلى العلاقة بين الفترة والتسارع الناتج عن الجاذبية.
تم نقل بندول مدته 2.00000 ثانية في موقع واحد (g = 9.80 m/s ²) إلى موقع جديد حيث تبلغ الفترة الآن 1.99796 ثانية، ما التسارع الناتج عن الجاذبية في موقعه الجديد؟
(أ) ما هو التأثير على فترة البندول إذا ضاعفت طوله؟ (ب) ما هو التأثير على فترة البندول إذا قمت بتقليل طوله بنسبة 5.00٪؟

15.5 تذبذبات مخمدة

تنخفض سعة المذبذب المخفف قليلاً بنسبة 3.0% خلال كل دورة. ما النسبة المئوية للطاقة الميكانيكية للمذبذب المفقودة في كل دورة؟

15.6 التذبذبات القسرية

ما مقدار الطاقة التي يجب أن تتبددها ممتصات الصدمات لسيارة وزنها ١٢٠٠ كجم من أجل ترطيب الارتداد الذي كانت سرعته في البداية ٠٫٨٠٠ م/ث في موضع الاتزان؟ افترض أن السيارة تعود إلى وضعها الرأسي الأصلي.
إذا كانت السيارة مزودة بنظام تعليق بقوة ثابتة تبلغ ٥٫٠٠ × ١٠ ^٤ نيوتن/م، فما مقدار الطاقة التي يجب أن تزيلها صدمات السيارة لتخفيف التذبذب الذي يبدأ بإزاحة قصوى مقدارها ٠٫٠٧٥٠ مترًا؟
(أ) ما مقدار زنبركي له قوة ثابتة قدرها 40.0 نيوتن/متر يتمدد بفعل جسم كتلته 0.500 كجم عند تعليقه من الزنبرك بلا حراك؟ (ب) احسب الانخفاض في طاقة وضع الجاذبية للجسم الذي يبلغ وزنه 0.500 كجم عند هبوطه على هذه المسافة. (ج) يذهب جزء من طاقة الجاذبية هذه إلى الربيع. احسب الطاقة المخزنة في الزنبرك بواسطة هذا الامتداد، وقارنها بالطاقة الكامنة للجاذبية. اشرح أين يمكن أن تذهب بقية الطاقة.
لنفترض أن لديك جسمًا وزنه 0.750 كجم على سطح أفقي متصل بنابض بقوة ثابتة 150 نيوتن/م، ويوجد احتكاك بسيط بين الجسم والسطح بمعامل احتكاك ثابت$\mu_{s}$ = 0.100. (أ) إلى أي مدى يمكن تمديد الزنبرك دون تحريك الكتلة؟ (ب) إذا وُضع الجسم في حالة تذبذب بسعة ضعف المسافة الموجودة في الجزء (أ)، وكان معامل الاحتكاك الحركي$\mu_{k}$ = 0.0850، فما المسافة الإجمالية التي يقطعها الجسم قبل توقفه؟ افترض أنه يبدأ عند السعة القصوى.

مشاكل إضافية

لنفترض أنك ربطت جسمًا كتلته m بنابض عمودي كان في الأصل في حالة سكون، وتركته يرتد لأعلى ولأسفل. تُحرّر الجسم من السكون عند طول السكون الأصلي للزنبرك، أي طول الزنبرك في حالة اتزان، دون ربط الكتلة به. سعة الحركة هي المسافة بين موضع توازن الزنبرك بدون الكتلة المرفقة وموضع توازن الزنبرك بالكتلة المرفقة. (أ) أظهر أن الزنبرك يمارس قوة تصاعدية قدرها 2.00 ملجم على الجسم عند أدنى نقطة له. (ب) إذا كانت قوة الزنبرك ثابتة مقدارها 10.0 نيوتن/م، وعُلِّق أفقيًا، وكان موضع الطرف الحر للزنبرك محددًا بـ y = 0.00 m، فأين موضع الاتزان الجديد إذا كان جسم كتلته 0.25 كجم مُعلَّقًا من الزنبرك؟ (ج) إذا كانت قوة الزنبرك ثابتة مقدارها 10.0 م/م وكان جسم كتلته 0.25 كجم يتحرك كما هو موضح، فأوجد سعة التذبذبات. (د) أوجد السرعة القصوى.
يخضع الغواص على لوح الغوص لـ SHM. كتلتها ٥٥٫٠ كجم ومدتها ٠٫٨۰ ثانية، والغطاس التالي هو ذكر مدة تذبذبه التوافقي البسيط ١٫٠٥ ثانية، ما كتلته إذا كانت كتلة اللوح ضئيلة؟
تردد 4.00 هرتز. تبلغ الكتلة الفعالة للوحة 10.0 كجم. ما تردد مقياس SHM لغواص وزنه ٧٥٫٠ كجم على متن الطائرة؟
يقوم الجهاز الموضح بالشكل التالي بترفيه الأطفال مع منعهم من التجول. يرتد الطفل في حزام معلق من إطار الباب بزنبرك. (أ) إذا كان الزنبرك يمتد لمسافة 0.250 مترًا بينما كان يعيل طفلًا وزنه 8.0 كجم، فما ثابت قوته؟ (ب) ما هو الوقت المناسب لارتداد كامل لهذا الطفل؟ (ج) ما السرعة القصوى للطفل إذا كانت سعة ارتداده 0.200 متر؟

صورة لطفل في حارس معلق. — الشكل 15-هاء 34 (المصدر: ليزا دوهنيرت)

تُوضع الكتلة على طاولة أفقية خالية من الاحتكاك. يتم وضع زنبرك (k = 100 نيوتن/م)، يمكن تمديده أو ضغطه، على الطاولة. يتم ربط كتلة مقدارها 5.00 كجم بأحد طرفي الزنبرك، بينما يتم تثبيت الطرف الآخر على الحائط. يتم وضع علامة على موضع التوازن عند الصفر. يحرك الطالب الكتلة إلى x = 4.0 سم ويخرجها من السكون. تتأرجح الكتلة في SHM. (أ) تحديد معادلات الحركة. (ب) أوجد موضع الكتلة وسرعتها وسرعتها في الوقت t = 3.00 ثانية.
أوجد نسبة الفترتين الجديدة/القديمة للبندول إذا كان البندول قد انتقل من الأرض إلى القمر، حيث تبلغ التسارع الناتج عن الجاذبية ١٫٦٣ م/ث ^٢.
ما معدَّل تشغيل ساعة البندول على القمر، حيث يبلغ التسارع الناتج عن الجاذبية 1.63 م/ث ²، إذا كانت تحافظ على الوقت بدقة على الأرض؟ أي، ابحث عن الوقت (بالساعات) الذي يستغرقه عقرب الساعة لإحداث ثورة واحدة على القمر.
إذا زادت الساعة التي يحركها البندول بمقدار 5.00 يوم/يوم، فما التغيير الجزئي في طول البندول الذي يجب إجراؤه للحفاظ على الوقت المثالي؟
جسم وزنه 2.00 كجم معلّق، أثناء الراحة، على خيط طوله 1.00 متر متصل بالسقف. تُطلق كتلة ١٠٠ جم بسرعة ٢٠ م/ث عند كتلة مقدارها ٢٫٠٠ كجم، وتتصادم الكتلة ١٠٠٫٠٠ جم بشكل مرن تمامًا مع الكتلة التي يبلغ وزنها ٢٫٠٠ كجم. اكتب معادلة لحركة الكتلة المعلقة بعد التصادم. افترض أن مقاومة الهواء ضئيلة.
جسم وزنه 2.00 كجم معلّق، أثناء الراحة، على خيط طوله 1.00 متر متصل بالسقف. أُطلق جسم وزنه ١٠٠ جم بسرعة ٢٠ م/ث على جسم وزنه ٢٫٠٠ كجم، ويصطدم الجسمان ويلتصقان معًا في تصادم غير مرن تمامًا. اكتب معادلة لحركة النظام بعد التصادم. افترض أن مقاومة الهواء ضئيلة.
افترض أن البندول المستخدم في قيادة ساعة الجد يبلغ طوله L ₀ = 1.00 m وكتلته M عند درجة حرارة T = 20.00 درجة مئوية، ويمكن تصميمه على هيئة بندول فيزيائي في صورة قضيب يتذبذب حول أحد طرفيه. ما النسبة المئوية التي ستتغير بها الفترة إذا ارتفعت درجة الحرارة بمقدار 10 درجات مئوية؟ افترض أن طول القضيب يتغير خطيًا مع درجة الحرارة، حيث L = L ₀ (1+$\alpha \Delta$ T) والقضيب مصنوع من النحاس ($\alpha$= 18 × 10 ⁻⁶° C ⁻¹).
كتلة وزنها 2.00 كجم تقع في وضع السكون على طاولة خالية من الاحتكاك. يتم تثبيت زنبرك ثابت زنبركي يبلغ 100 نيوتن/متر بالجدار والكتلة. يتم وضع كتلة ثانية وزنها 0.50 كجم فوق الكتلة الأولى. يتم سحب الكتلة التي يبلغ وزنها 2.00 كجم بلطف إلى الموضع x = + A وتحريرها من السكون. يوجد معامل احتكاك قدره 0.45 بين الكتلتين. (أ) ما هي فترة التذبذبات؟ (ب) ما هي أكبر سعة للحركة تسمح للكتل بالتأرجح دون انزلاق الكتلة التي يبلغ وزنها 0.50 كجم؟

مشاكل التحدي

يتذبذب جسر معلق بقوة فعَّالة ثابتة مقدارها 1.00 x 10 ⁸ نيوتن/م. (أ) ما مقدار الطاقة اللازمة لجعله يتذبذب بسعة 0.100 m؟ (ب) إذا سار الجنود عبر الجسر بإيقاع يساوي التردد الطبيعي للجسر ونقلوا طاقة قدرها 1.00 x 10 ⁴ J في كل ثانية، ما المدة التي تستغرقها تذبذبات الجسر لتنتقل من 0.100 متر إلى 0.500 متر.
بالقرب من الجزء العلوي من مبنى Citigroup Center في مدينة نيويورك، يوجد جسم كتلته 4.00 × 10 ⁵ كجم على نوابض ذات ثوابت قوة قابلة للتعديل. وتتمثل مهمتها في تثبيط تذبذبات المبنى التي تحركها الرياح عن طريق التذبذب بنفس التردد الذي يتم فيه قيادة المبنى - يتم نقل القوة الدافعة إلى الكائن الذي يتأرجح بدلاً من المبنى بأكمله. (أ) ما هو ثابت القوة الفعَّالة الذي ينبغي أن تحتويه النوابض لجعل الجسم يتذبذب بمدَّة مقدارها 2.00 ثانية؟ (ب) ما الطاقة المخزنة في الينابيع لإزاحة مسافة 2.00 متر عن حالة الاتزان؟
يمكن أن تتأرجح طرود الهواء (كميات صغيرة من الهواء) في جو مستقر (حيث تزداد درجة الحرارة مع الارتفاع) لأعلى ولأسفل، بسبب قوة الاستعادة التي يوفرها طفو الطرد الجوي. تردد التذبذبات هو مقياس لاستقرار الغلاف الجوي. بافتراض أن تسريع الطرد الجوي يمكن تصميمه على أنه حل$\frac{\partial^{2} z}{\partial t^{2}} = \frac{g \partial \rho (z)}{\rho_{0} \partial z} z'$، أثبت أن هذا$z' = z'_{0} e^{t \sqrt{-N^{2}}}$ هو الحل، حيث يُعرف N بتردد Brunt-Väisälä. لاحظ أنه في جو مستقر، تنخفض الكثافة مع الارتفاع وتتأرجح الطرود لأعلى ولأسفل.
ضع في اعتبارك جهد فان دير فال U (r) = U ₀$\Bigg[ \left(\dfrac{R_{0}}{r}\right)^{2} - 2 \left(\dfrac{R_{0}}{r}\right)^{6} \Bigg] $، المستخدم لنمذجة دالة الطاقة الكامنة لجزيئين، حيث يكون الحد الأدنى للجهد عند r = R ₀. ابحث عن القوة كدالة لـ r. ضع في اعتبارك الإزاحة الصغيرة r = R ₀ + r′ واستخدم نظرية ذات الحدين: $$ (1 + x) ^ {n} = 1 + nx +\ frac {n (n-1)} {2!} x^ {2} +\ frac {n (n - 1) (n - 2)} {3!} x^ {3} +\ cdots$$، لإظهار أن القوة تقارب قوة قانون هوك.
لنفترض أن طول بندول الساعة قد تغير بنسبة 1.000%، بالضبط عند ظهر أحد الأيام. ما الوقت الذي ستقرأ فيه الساعة بعد 24.00 ساعة، بافتراض أن البندول حافظ على الوقت المثالي قبل التغيير؟ لاحظ أن هناك إجابتين، وقم بإجراء الحساب بدقة مكونة من أربعة أرقام.
(أ) تعمل نوابض الشاحنة الصغيرة مثل زنبرك وحيد بقوة ثابتة تبلغ 1.30 x 10 ⁵ نيوتن/م، ما مقدار الضغط الذي ستتعرض له الشاحنة بسبب حمولتها القصوى البالغة 1000 كجم؟ (ب) إذا كانت الشاحنة الصغيرة تحتوي على أربعة نوابض متطابقة، فما ثابت قوة كل منها؟