15.7: التذبذبات القسرية
- Page ID
- 200131
- تعريف التذبذبات القسرية
- ضع قائمة بمعادلات الحركة المرتبطة بالتذبذبات القسرية
- شرح مفهوم الرنين وتأثيره على سعة المذبذب
- ضع قائمة بخصائص النظام الذي يتذبذب بالرنين
اجلس أمام البيانو في وقت ما وقم بغناء نغمة قصيرة بصوت عالٍ مع إزالة المخمدات من خيوطه (الشكل\(\PageIndex{1}\)). ستغني نفس النغمة إليك - الأوتار، التي لها نفس ترددات صوتك، ترد استجابة لقوى الموجات الصوتية التي أرسلتها إليها. هذا مثال جيد على حقيقة أن الأشياء - في هذه الحالة، أوتار البيانو - يمكن إجبارها على التذبذب والتأرجح بسهولة عند ترددها الطبيعي. في هذا القسم، نستكشف بإيجاز تطبيق قوة دافعة دورية تعمل على مذبذب توافقي بسيط. تضع القوة الدافعة الطاقة في النظام بتردد معين، وليس بالضرورة نفس التردد الطبيعي للنظام. تذكر أن التردد الطبيعي هو التردد الذي سيتذبذب به النظام إذا لم تكن هناك قيادة ولا قوة تخميد.

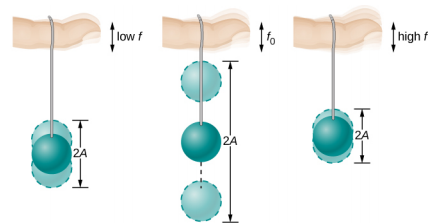
لقد لعب معظمنا بالألعاب التي تتضمن شيئًا مدعومًا على شريط مطاطي، مثل كرة المضرب المعلقة من إصبع في الشكل\(\PageIndex{2}\). تخيل أن الإصبع في الشكل هو إصبعك. في البداية، يمكنك تثبيت إصبعك بثبات، وترتد الكرة لأعلى ولأسفل بكمية صغيرة من التخميد. إذا قمت بتحريك إصبعك لأعلى ولأسفل ببطء، ستتبعها الكرة دون أن ترتد كثيرًا من تلقاء نفسها. عندما تقوم بزيادة التردد الذي تحرك به إصبعك لأعلى ولأسفل، تستجيب الكرة بالتأرجح بسعة متزايدة. عندما تقود الكرة بترددها الطبيعي، تزداد تذبذبات الكرة في السعة مع كل تذبذب طوال فترة قيادتك لها. تسمى ظاهرة قيادة نظام بتردد يساوي تردده الطبيعي بالرنين. يُقال إن النظام الذي يتم تشغيله بتردده الطبيعي يتردد صداه. عندما يزداد تردد القيادة تدريجيًا عن الرنين أو التردد الطبيعي، يصبح اتساع التذبذبات أصغر حتى تختفي التذبذبات تقريبًا، ويتحرك إصبعك ببساطة لأعلى ولأسفل مع تأثير ضئيل على الكرة.
فكر في تجربة بسيطة. اربط كتلة m بنابض في سائل لزج، على غرار الجهاز الذي تمت مناقشته في المذبذب التوافقي المثبط. هذه المرة، بدلاً من إصلاح الطرف الحر للزنبرك، قم بتوصيل الطرف الحر بقرص يتم تشغيله بواسطة محرك متغير السرعة. يدور المحرك بتردد قيادة زاوي يبلغ Ω. يوفر القرص الدوار الطاقة للنظام من خلال العمل الذي تقوم به القوة الدافعة (F d = F 0 sin (\(\omega\)t)). يظهر الجهاز التجريبي في الشكل\(\PageIndex{3}\).
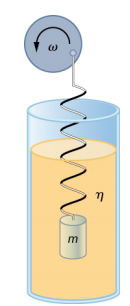
باستخدام قانون نيوتن الثاني (\(\vec{F}_{net} = m \vec{a}\))، يمكننا تحليل حركة الكتلة. المعادلة الناتجة مشابهة لمعادلة القوة للمذبذب التوافقي المثبط، مع إضافة القوة الدافعة:
\[-kx -b \frac{dx}{dt} + F_{0} \sin (\omega t) = m \frac{d^{2} x}{dt^{2}} \ldotp \label{15.27}\]
عندما يتم دفع المذبذب بقوة دافعة دورية، قد تبدو الحركة فوضوية. تُعرف حركات المذبذب باسم العابرين. بعد موت العابرين، يصل المذبذب إلى حالة ثابتة، حيث تكون الحركة دورية. بعد مرور بعض الوقت، يكون حل الحالة الثابتة لهذه المعادلة التفاضلية
\[x(t) = A \cos (\omega t + \phi) \ldotp \label{15.28}\]
مرة أخرى، يُترك الأمر كتمرين لإثبات أن هذه المعادلة هي الحل. يُظهر أخذ المشتق الأول والثاني لـ x (t) واستبدالهما في معادلة القوة أن x (t) = Asin (\(\omega t + \phi\)) هو الحل طالما أن السعة تساوي
\[A = \frac{F_{0}}{\sqrt{m^{2} (\omega^{2} - \omega_{0}^{2})^{2} + b^{2} \omega^{2}}} \label{15.29}\]
أين\(\omega_{0} = \sqrt{\frac{k}{m}}\) هو التردد الزاوي الطبيعي لنظام الكتلة والربيع. تذكر أنه يمكن تعديل التردد الزاوي، وبالتالي التردد، للمحرك. عند النظر إلى مقام معادلة السعة، عندما يكون تردد القيادة أصغر بكثير، أو أكبر بكثير، من التردد الطبيعي،\((\omega^{2} − \omega_{0}^{2})^{2}\) يكون مربع الفرق بين الترددين الزاويين موجبًا وكبيرًا، مما يجعل المقام كبيرًا، والنتيجة هي سعة صغيرة لـ تذبذبات الكتلة. عندما يقترب تردد القوة الدافعة من التردد الطبيعي للنظام، يصبح المقام صغيرًا وتصبح سعة التذبذبات كبيرة. ينتج الحد الأقصى للسعة عندما يساوي تردد القوة الدافعة التردد الطبيعي للنظام (A max =\(\frac{F_{0}}{b \omega}\)).
\(\PageIndex{4}\)يوضح الشكل رسمًا بيانيًا لسعة المذبذب التوافقي المثبط كدالة لتردد القوة الدورية الدافعة له. يمثل كل منحنى من المنحنيات الثلاثة على الرسم البياني مقدارًا مختلفًا من التخميد. تبلغ جميع المنحنيات الثلاثة ذروتها عند النقطة التي يساوي فيها تردد القوة الدافعة التردد الطبيعي للمذبذب التوافقي. أعلى قمة، أو أكبر استجابة، هي أقل قدر من التخميد، لأنه يتم إزالة كمية أقل من الطاقة بواسطة قوة التخميد. لاحظ أنه نظرًا لأن السعة تنمو مع انخفاض التخميد، مع أخذ هذا إلى الحد الذي لا يوجد فيه تخميد (b = 0)، تصبح السعة غير محدودة.
لاحظ أن القوة الدافعة ذات السعة الصغيرة يمكن أن تنتج استجابة ذات سعة كبيرة. تعرف هذه الظاهرة باسم الرنين. من الأمثلة الشائعة للرنين قيام أحد الوالدين بدفع طفل صغير على الأرجوحة. عندما يرغب الطفل في الارتفاع، لا يعود الوالد إلى الوراء، ثم يبدأ في الجري، ويصطدم بالطفل، ويطبق قوة كبيرة في فترة زمنية قصيرة. بدلاً من ذلك، يقوم الوالد بتطبيق دفعات صغيرة على الطفل بالتردد الصحيح فقط، وتزداد سعة تقلبات الطفل.
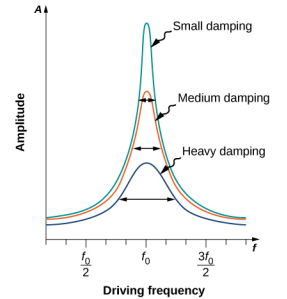
من المثير للاهتمام ملاحظة أن عرض منحنيات الرنين الموضحة في الشكل\(\PageIndex{4}\) يعتمد على التخميد: فكلما قل التخميد، كلما كان الرنين أضيق. والنتيجة هي أنك إذا كنت تريد أن يتردد صدى مذبذب مدفوع بتردد محدد جدًا، فأنت بحاجة إلى أقل قدر ممكن من التخميد. على سبيل المثال، يحتوي الراديو على دائرة تُستخدم لاختيار محطة راديو معينة. في هذه الحالة، يتكون المذبذب التخميد القسري من المقاوم والمكثف والمحث، والتي ستتم مناقشتها لاحقًا في هذه الدورة. يتم «ضبط» الدائرة لاختيار محطة إذاعية معينة. من المستحسن هنا أن يكون منحنى الرنين ضيقًا جدًا، لاختيار التردد الدقيق لمحطة الراديو المختارة. يُعرف ضيق الرسم البياني والقدرة على اختيار تردد معين بجودة النظام. تُعرّف الجودة بأنها انتشار التردد الزاوي، أو ما يعادل الانتشار في التردد، بنصف السعة القصوى، مقسومًا على التردد الطبيعي (Q =\(\frac{\Delta \omega}{\omega_{0}}\)) كما هو موضح في الشكل\(\PageIndex{5}\). بالنسبة للتخميد الصغير، تكون الجودة مساوية تقريبًا لـ Q ≈\(\frac{2b}{m}\).
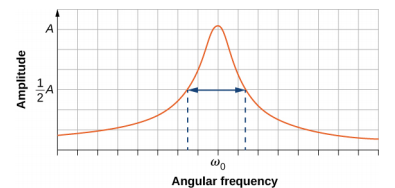
تنطبق ميزات المذبذبات التوافقية المدفوعة على مجموعة كبيرة ومتنوعة من الأنظمة. على سبيل المثال، يعد التصوير بالرنين المغناطيسي (MRI) أداة تشخيص طبية مستخدمة على نطاق واسع حيث يتم تصنيع النوى الذرية (معظمها نوى الهيدروجين أو البروتونات) لتردد صداها بواسطة موجات الراديو الواردة (في حدود 100 ميجاهرتز). في كل هذه الحالات، تكون كفاءة نقل الطاقة من القوة الدافعة إلى المذبذب هي الأفضل عند الرنين. \(\PageIndex{6}\)يُظهر الشكل جسر لندن ميلينيوم فوتبريدج الذي يسمح للمشاة بعبور نهر التايمز في لندن. أطلق على هذا الجسر اسم «Wobbly Bridge» عندما اختبر المشاة حركة متمايلة أثناء عبوره. تم إغلاق الجسر لمدة عامين تقريبًا للتخلص من هذه الحركة.

تتضمن الحيلة السحرية الشهيرة فنانًا يغني نوتة باتجاه الزجاج البلوري حتى يتحطم الزجاج. اشرح لماذا تعمل الخدعة من حيث الرنين والتردد الطبيعي.


