Skip to main content
Global

15.6: تذبذبات مخمدة

  1. Last updated
  2. Save as PDF
  • Page ID
    200119

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم
    • وصف حركة الحركة التوافقية المثبطة
    • اكتب معادلات الحركة للتذبذبات التوافقية المثبطة
    • وصف حركة الحركة التوافقية المحركة أو القسرية
    • اكتب معادلات الحركة للحركة التوافقية القسرية المُخمدة

    في العالم الحقيقي، نادرًا ما تتبع التذبذبات SHM الحقيقي. عادة ما يعمل الاحتكاك من نوع ما على تثبيط الحركة بحيث تموت أو تحتاج إلى مزيد من القوة للمتابعة. في هذا القسم، ندرس بعض الأمثلة للحركة التوافقية المثبطة ونرى كيفية تعديل معادلات الحركة لوصف هذه الحالة الأكثر عمومية.

    تتوقف سلسلة الجيتار عن التأرجح بعد بضع ثوانٍ من التقاطها. للاستمرار في التأرجح على أرجوحة الملعب، يجب أن تستمر في الضغط (الشكل\(\PageIndex{1}\)). على الرغم من أننا غالبًا ما نجعل الاحتكاك والقوى غير المحافظة الأخرى صغيرة أو ضئيلة، إلا أن الحركة غير المثبطة تمامًا نادرة. في الواقع، قد نرغب أيضًا في ترطيب التذبذبات، مثل ممتصات صدمات السيارات.

    صورة لشخص على أرجوحة
    الشكل\(\PageIndex{1}\): لمواجهة قوى التخميد، تحتاج إلى الاستمرار في ضخ الأرجوحة. (تصوير: بوب ميكال)

    \(\PageIndex{2}\)يوضِّح الشكل كتلة m متصلة بنابض بقوة ثابتة k. وتُرفع الكتلة إلى الموضع A 0، السعة الأولية، ثم تُحرَّر. تتأرجح الكتلة حول موضع التوازن في مائع ذي لزوجة ولكن السعة تنخفض لكل تذبذب. بالنسبة للنظام الذي يحتوي على كمية صغيرة من التخميد، تكون الفترة والتردد ثابتين وهما تقريبًا نفس نظام SHM، لكن السعة تتناقص تدريجيًا كما هو موضح. يحدث هذا لأن قوة التخميد غير المحافظة تزيل الطاقة من النظام، وعادة ما تكون في شكل طاقة حرارية.

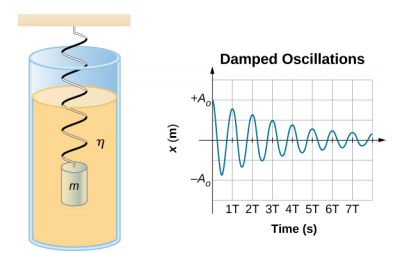
    تُعلَّق الكتلة m من زنبرك عمودي وتُغمر في سائل يحتوي على مقدار اللزوجة. يُظهر الرسم البياني للتذبذب المثبط الإزاحة x بالأمتار على المحور الرأسي كدالة للوقت بالثواني على المحور الأفقي. يتراوح نطاق x من ناقص A دون الصفر إلى زائد A دون الصفر. ويتراوح المقياس الزمني من صفر إلى 7 درجات مئوية، مع وجود التشنجات اللاإرادية بزيادات قدرها T. وتكون الإزاحة زائدًا A دون الصفر في الوقت صفر وتتأرجح بين الحد الأقصى الموجب والحد الأدنى السالب، حيث تستغرق كل دورة كاملة نفس الوقت T ولكن سعة التذبذبات تتناقص بمرور الوقت.
    الشكل\(\PageIndex{2}\): بالنسبة لكتلة على زنبرك تتأرجح في سائل لزج، تظل الفترة ثابتة، لكن سعة التذبذبات تنخفض بسبب التخميد الناجم عن السائل.

    فكر في القوى المؤثرة على الكتلة. لاحظ أن المساهمة الوحيدة للوزن هي تغيير موضع التوازن، كما تمت مناقشته سابقًا في الفصل. لذلك، فإن القوة الصافية تساوي قوة الزنبرك وقوة التخميد (\(F_D\)). إذا كان حجم السرعة صغيرًا، مما يعني أن الكتلة تتأرجح ببطء، فإن قوة التخميد تتناسب مع السرعة وتعمل ضد اتجاه الحركة (\(F_D = −b\)). وبالتالي فإن القوة الصافية المؤثرة على الكتلة هي

    \[ma = -bv - kx \ldotp\]

    عند كتابة هذا كمعادلة تفاضلية في x، نحصل عليه

    \[m \frac{d^{2} x}{dt^{2}} + b \frac{dx}{dt} + kx = 0 \ldotp \label{15.23}\]

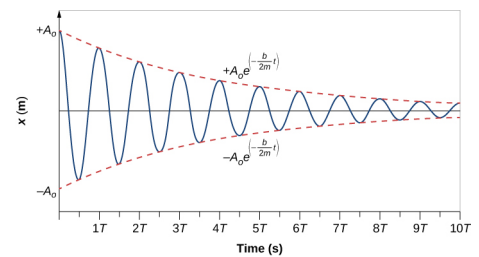
    لتحديد حل هذه المعادلة، ضع في اعتبارك مخطط الموضع مقابل الوقت الموضح في الشكل\(\PageIndex{3}\). يشبه المنحنى منحنى جيب التمام يتأرجح في غلاف الدالة الأسية\(A_0e^{−\alpha t}\) حيث\(\alpha = \frac{b}{2m}\). الحل هو

    \[x(t) = A_{0} e^{- \frac{b}{2m} t} \cos (\omega t + \phi) \ldotp \label{15.24}\]

    يُترك الأمر كتمرين لإثبات أن هذا هو، في الواقع، الحل. لإثبات أنه الحل الصحيح، خذ المشتقين الأول والثاني فيما يتعلق بالوقت واستبدلهما في المعادلة 15.23. وجد أن المعادلة 15.24 هي الحل إذا

    \[\omega = \sqrt{\frac{k}{m} - \left(\dfrac{b}{2m}\right)^{2}} \ldotp\]

    تذكر أن التردد الزاوي للكتلة التي تمر بـ SHM يساوي الجذر التربيعي لثابت القوة مقسومًا على الكتلة. غالبًا ما يشار إلى هذا بالتردد الزاوي الطبيعي، والذي يتم تمثيله كـ

    \[\omega_{0} = \sqrt{\frac{k}{m}} \ldotp \label{15.25}\]

    يصبح التردد الزاوي للحركة التوافقية المبللة

    \[\omega = \sqrt{\omega_{0}^{2} - \left(\dfrac{b}{2m}\right)^{2}} \ldotp \label{15.26}\]

    يوضِّح الشكل رسمًا بيانيًا للإزاحة، x بالأمتار، على طول المحور الرأسي، مقابل الوقت بالثواني على طول المحور الأفقي. تتراوح الإزاحة من ناقص A دون الصفر إلى زائد A دون الصفر ويتراوح الوقت من 0 إلى 10 T. تتأرجح الإزاحة، الموضحة بالمنحنى الأزرق، بين الحد الأقصى الموجب والحد الأدنى السالب، لتشكل موجة تتناقص اتساعها تدريجيًا عندما نتحرك بعيدًا عن t=0. يظل الوقت، T، بين القمم المتجاورة هو نفسه طوال الوقت. يظهر الظرف، وهو المنحنى الأملس الذي يربط القمم ومنحنى أملس آخر يربط بين قيعان التذبذبات، كزوج من الخطوط الحمراء المتقطعة. يُطلق على المنحنى العلوي الذي يربط القمم علامة زائد A دون الصفر مضروبًا في e إلى الكمية ناقص b t على 2 م. ويُسمى المنحنى السفلي الذي يربط بين الحوضين بأنه ناقص A دون الصفر مضروبًا في e إلى الكمية ناقص b t على 2 م.
    الشكل\(\PageIndex{3}\): الموضع مقابل الزمن للكتلة المتذبذبة على زنبرك في سائل لزج. لاحظ أن المنحنى يبدو وكأنه دالة جيب التمام داخل ظرف أسي.

    تذكر أنه عندما بدأنا هذا الوصف للحركة التوافقية المخففة، ذكرنا أن التخميد يجب أن يكون صغيرًا. يتبادر إلى الذهن سؤالان. لماذا يجب أن يكون التخميد صغيرًا؟ وما مدى صغر حجمها؟ إذا قمت بزيادة كمية التخميد في النظام تدريجيًا، تبدأ الفترة والتردد في التأثر، لأن التخميد يعارض وبالتالي يبطئ الحركة ذهابًا وإيابًا. (القوة الصافية أصغر في كلا الاتجاهين.) إذا كان هناك تخميد كبير جدًا، فإن النظام لا يتأرجح حتى - يتحرك ببطء نحو التوازن. التردد الزاوي يساوي

    \[\omega = \sqrt{\frac{k}{m} - \left(\dfrac{b}{2m}\right)^{2}} \ldotp\]

    كلما زاد b،\(\frac{k}{m} - \left(\dfrac{b}{2m}\right)^{2}\) يصبح أصغر ويصل في النهاية إلى الصفر عندما b =\(\sqrt{4mk}\). إذا أصبح b أكبر،\(\frac{k}{m} - \left(\dfrac{b}{2m}\right)^{2}\) يصبح رقمًا سالبًا\(\sqrt{\frac{k}{m} - \left(\dfrac{b}{2m}\right)^{2}}\) ورقمًا مركبًا.

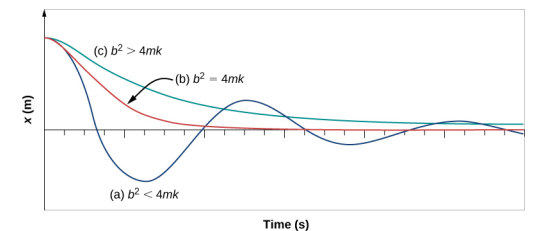
    الموضع، x بالأمتار على المحور الرأسي، مقابل الوقت بالثواني على المحور الأفقي، بدرجات متفاوتة من التخميد. لم يتم إعطاء مقياس لأي من المحورين. تبدأ جميع المنحنيات الثلاثة في نفس الموضع الإيجابي في الوقت صفر. المنحنى الأزرق a، المسمى بـ b squared هو أقل من 4 أمتار كلفن، ويخضع لما يزيد قليلاً عن اثنين وربع من التذبذبات ذات السعة المتناقصة والفترة الثابتة. المنحنى الأحمر b، المسمى بـ b squared يساوي 4 م k، وينخفض عند t = 0 بسرعة أقل من المنحنى الأزرق، لكنه لا يتذبذب. يقترب المنحنى الأحمر من x=0 بشكل متقارب، ويكون صفرًا تقريبًا ضمن تذبذب واحد من المنحنى الأزرق. المنحنى الأخضر c، المسمى بـ b squared أكبر من 4 م k، وينخفض عند t = 0 بسرعة أقل من المنحنى الأحمر، ولا يتذبذب. يقترب المنحنى الأخضر من x=0 بشكل متقارب، لكنه لا يزال أعلى بشكل ملحوظ من الصفر في نهاية الرسم البياني، بعد أكثر من تذبذبين للمنحنى الأزرق.
    الشكل\(\PageIndex{4}\): الموضع مقابل الزمن لثلاثة أنظمة تتكون من كتلة وزنبرك في سائل لزج. (أ) إذا كان التخميد صغيرًا (b <\(\sqrt{4mk}\))، تتأرجح الكتلة وتفقد السعة ببطء عندما تتبدد الطاقة بفعل القوة (القوى) غير المحافظة. الحالة المقيدة هي (ب) حيث يكون التخميد (b =\(\sqrt{4mk}\)). (ج) إذا كان التخميد كبيرًا جدًا (b >\(\sqrt{4mk}\))، فإن الكتلة لا تتأرجح عند إزاحتها، ولكنها تحاول العودة إلى وضع التوازن.

    \(\PageIndex{4}\)يوضح الشكل إزاحة المذبذب التوافقي لكميات مختلفة من التخميد.

    1. عندما يكون ثابت التخميد صغيرًا\(\sqrt{4mk}\)، b <، يتأرجح النظام بينما تتحلل سعة الحركة بشكل كبير. يُقال أن هذا النظام ضعيف، كما هو الحال في المنحنى (أ). يتم تثبيط العديد من الأنظمة وتتذبذب بينما تنخفض السعة بشكل كبير، مثل تذبذب الكتلة على الزنبرك. قد يكون التخميد صغيرًا جدًا، ولكن في النهاية تهدأ الكتلة.
    2. إذا كان ثابت التخميد\(b = \sqrt{4mk}\)، يُقال إن النظام مثبط بشكل خطير، كما هو الحال في curve (\(b\)). يعد امتصاص الصدمات في السيارة مثالاً على نظام التخميد الشديد. من المفيد أن تتحلل التذبذبات في أسرع وقت ممكن. هنا، لا يتذبذب النظام، ولكنه يقترب من حالة التوازن في أسرع وقت ممكن.
    3. \(\PageIndex{4}\)يمثل المنحنى (ج) في الشكل نظامًا مثقلًا حيث\(b > \sqrt{4mk}\). سوف يقترب النظام المثقل من التوازن على مدى فترة زمنية أطول.

    غالبًا ما يكون التخميد الحرج مطلوبًا، لأن مثل هذا النظام يعود إلى التوازن بسرعة ويبقى في حالة توازن أيضًا. بالإضافة إلى ذلك، تعمل القوة الثابتة المطبقة على النظام المثبط بشدة على نقل النظام إلى موضع توازن جديد في أقصر وقت ممكن دون تجاوز الحد أو التذبذب حول الموضع الجديد.

    التمارين الرياضية\(\PageIndex{1}\)

    لماذا تكون المذبذبات التوافقية غير المثبطة تمامًا نادرة جدًا؟