15.5: البندول

Last updated
Save as PDF

Page ID: 200090

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

أهداف التعلم

اذكر القوى التي تعمل على بندول بسيط
حدد التردد الزاوي والتردد والفترة للبندول البسيط من حيث طول البندول والتسارع الناتج عن الجاذبية
حدد فترة البندول المادي
حدد فترة البندول الالتوائي

البندول شائعة الاستخدام. تستخدم ساعات الجد البندول للحفاظ على الوقت ويمكن استخدام البندول لقياس التسارع بسبب الجاذبية. بالنسبة لعمليات الإزاحة الصغيرة، فإن البندول هو مذبذب توافقي بسيط.

البندول البسيط

يُعرَّف البندول البسيط بأنه يحتوي على كتلة نقطية، تُعرف أيضًا باسم بوب البندول، والتي يتم تعليقها من سلسلة طولها L بكتلة ضئيلة (الشكل$\PageIndex{1}$). هنا، القوى الوحيدة المؤثرة على البوب هي قوة الجاذبية (أي وزن البوب) والتوتر من الخيط. من المفترض أن تكون كتلة السلسلة ضئيلة مقارنة بكتلة البوب.

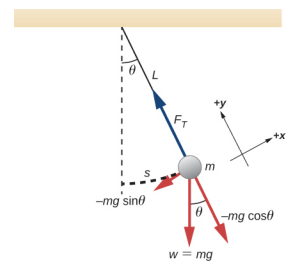
في الشكل، يظهر شريط أفقي. خيط طوله L يمتد من الشريط بزاوية ثيتا بعكس اتجاه عقارب الساعة من الرأسي. يُشار إلى الاتجاه الرأسي بخط متقطع يمتد لأسفل من حيث يتم ربط السلسلة بالشريط. يتم توصيل كتلة دائرية كتلتها m بالطرف السفلي من السلسلة. يُشار إلى القوس الممتد من الكتلة إلى العمود بخط متقطع آخر ويبلغ طوله s، ويظهر سهم أحمر يوضح الوقت T لتذبذب الغوغاء على طول الخط الوتري باتجاه الشريط. يظهر نظام الإحداثيات بالقرب من البوب بحيث يكون اتجاه y الموجب محاذيًا للخيط ويشير إلى النقطة المحورية واتجاه x الموجب الذي يشير إلى المماس إلى القوس وبعيدًا عن موضع التوازن. يُطلق على السهم الأزرق المتجه من البوب باتجاه المحور، على طول الوتر، اسم F sub T. ويُسمى السهم الأحمر من البوب المتجه لأسفل w = m g. أما السهم الأحمر الذي يشير إلى القوس ونحو التوازن، في اتجاه ناقص x، فيسمى ناقص m g sine theta. يُطلق على السهم الأحمر بزاوية theta بعكس اتجاه عقارب الساعة من w علامة ناقص m g. — الشكل$\PageIndex{1}$: يحتوي البندول البسيط على بوب ذو قطر صغير وخيط له كتلة صغيرة جدًا ولكنه قوي بما يكفي لعدم التمدد بشكل ملحوظ. الإزاحة الخطية من حالة الاتزان هي s، وهي طول القوس. كما تظهر أيضًا القوى المؤثِّرة على البوب، التي تؤدِّي إلى قوة صافية مقدارها −mgsin في$\theta$ اتجاه موضع الاتزان، أي قوة استعادة.

ضع في اعتبارك عزم الدوران على البندول. القوة التي توفر عزم الاستعادة هي مكون وزن بوب البندول الذي يعمل على طول القوس. عزم الدوران هو طول السلسلة L مضروبًا في مكون القوة الصافية المتعامدة مع نصف قطر القوس. تشير علامة الطرح إلى أن عزم الدوران يعمل في الاتجاه المعاكس للإزاحة الزاوية:

\[\begin{split} \tau & = -L (mg \sin \theta); \\ I \alpha & = -L (mg \sin \theta); \\ I \frac{d^{2} \theta}{dt^{2}} & = -L (mg \sin \theta); \\ mL^{2} \frac{d^{2} \theta}{dt^{2}} & = -L (mg \sin \theta); \\ \frac{d^{2} \theta}{dt^{2}} & = - \frac{g}{L} \sin \theta \ldotp \end{split}\]

يتضمن حل هذه المعادلة التفاضلية حساب التفاضل والتكامل المتقدم، وهو خارج نطاق هذا النص. ولكن لاحظ أنه بالنسبة للزوايا الصغيرة (أقل من 15 درجة)،$\theta$ تختلف الخطيئة$\theta$ بنسبة أقل من 1٪، لذلك يمكننا استخدام زاوية تقريب الزاوية الصغيرة sin$\theta$ ≈$\theta$. $\theta$تصف الزاوية موضع البندول. استخدام تقريب الزاوية الصغيرة يعطي حلاً تقريبيًا للزوايا الصغيرة،

\[\frac{d^{2} \theta}{dt^{2}} = - \frac{g}{L} \theta \ldotp \label{15.17}\]

نظرًا لأن هذه المعادلة لها نفس شكل معادلة SHM، فمن السهل العثور على الحل. التردد الزاوي هو

\[\omega = \sqrt{\frac{g}{L}} \label{15.18}\]

وهذه الفترة هي

\[T = 2 \pi \sqrt{\frac{L}{g}} \ldotp \label{15.19}\]

تعتمد فترة البندول البسيط على طوله والتسارع بسبب الجاذبية. هذه الفترة مستقلة تمامًا عن العوامل الأخرى، مثل الكتلة والحد الأقصى للنزوح. كما هو الحال مع المذبذبات التوافقية البسيطة، تكون الفترة T للبندول مستقلة تقريبًا عن السعة، خاصة إذا كانت$\theta$ أقل من حوالي 15 درجة. حتى ساعات البندول البسيطة يمكن تعديلها بدقة وتبقى دقيقة.

لاحظ اعتماد T على g. إذا كان طول البندول معروفًا بدقة، فيمكن استخدامه فعليًا لقياس التسارع الناتج عن الجاذبية، كما في المثال التالي.

مثال$\PageIndex{1}$: Measuring Acceleration due to Gravity by the Period of a Pendulum

ما مقدار التسارع الناتج عن الجاذبية في منطقة يبلغ فيها البندول البسيط الذي يبلغ طوله ٧٥٠٠٠ سم مسافة ١٫٧٣٥٧ ثانية؟

إستراتيجية

يُطلب منا إيجاد g بمعلومية الفترة T والطول L للبندول. يمكننا حل T = 2$\pi$ L g لـ g، بافتراض أن زاوية الانحراف أقل من 15 درجة فقط.

الحل

المربع T = 2$\pi \sqrt{\frac{L}{g}}$ وحل لـ g: $$g = 4\ pi^ {2}\ frac {L} {T^ {2}} ldotp$$
استبدل القيم المعروفة بالمعادلة الجديدة: $$g = 4\ pi^ {2}\ frac {0.75000\; m} {(1.7357\; s) ^ {2}}\ ldotp$$
احسب للعثور على g: $$g = 9.8281\; م/s^ {2}\ ldotp$$

الدلالة

يمكن أن تكون هذه الطريقة لتحديد g دقيقة للغاية، ولهذا السبب يتم إعطاء الطول والفترة لخمسة أرقام في هذا المثال. $\theta$لكي تكون دقة خط التقريب$\theta$ ≈ أفضل من دقة طول البندول ومدته، يجب أن تظل زاوية الإزاحة القصوى أقل من 0.5 درجة تقريبًا.

التمارين$\PageIndex{1}$

يقوم مهندس ببناء بندولين بسيطين. كلاهما معلق من أسلاك صغيرة مثبتة في سقف الغرفة. يحوم كل بندول على ارتفاع 2 سم فوق الأرض. البندول 1 له بوب كتلته 10 كجم. يحتوي البندول 2 على بوب كتلته 100 كجم. وصف كيف ستختلف حركة البندول إذا تم إزاحة كل من البكرات بمقدار 12 درجة.

البندول الفيزيائي

يمكن لأي كائن أن يتذبذب مثل البندول. ضع في اعتبارك كوب قهوة معلق على خطاف في المخزن. إذا تم ضرب الكوب، فإنه يتأرجح ذهابًا وإيابًا مثل البندول حتى تختفي التذبذبات. لقد وصفنا البندول البسيط بأنه كتلة نقطية وخيط. البندول المادي هو أي جسم تتشابه تذبذباته مع تذبذبات البندول البسيط، ولكن لا يمكن نمذجته ككتلة نقطية على سلسلة، ويجب تضمين التوزيع الكتلي في معادلة الحركة.

أما بالنسبة للبندول البسيط، فإن قوة استعادة البندول المادي هي قوة الجاذبية. باستخدام البندول البسيط، تعمل قوة الجاذبية على مركز البندول. في حالة البندول المادي، تعمل قوة الجاذبية على مركز الكتلة (CM) للجسم. يتذبذب الكائن حول النقطة O. ضع في اعتبارك كائنًا ذا شكل عام كما هو موضح في الشكل$\PageIndex{2}$.

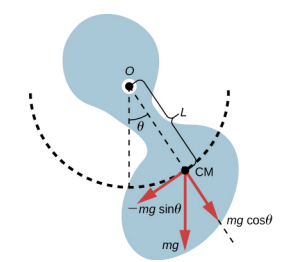
رسم البندول المادي. في الشكل، البندول عبارة عن جسم غير منتظم الشكل. مركز الكتلة، C M، هو المسافة L من النقطة المحورية، O. يتتبع مركز الكتلة قوسًا دائريًا، متمركزًا عند O. يصنع الخط من O إلى L زاوية ثيتا بعكس اتجاه عقارب الساعة من الرأسي. تم تصوير ثلاث قوى بواسطة السهام الحمراء في مركز الكتلة. تشير القوة m g إلى الأسفل. ومكوناته هي ناقص m g sine theta الذي يشير إلى المماس إلى القوس الذي يتبعه مركز الكتلة، وm g جيب التمام theta الذي يشير شعاعيًا إلى الخارج. — الشكل$\PageIndex{2}$: البندول المادي هو أي كائن يتأرجح في صورة بندول، ولكن لا يمكن نمذجته ككتلة نقطية على سلسلة. تعمل قوة الجاذبية على مركز الكتلة (CM) وتوفر قوة الاستعادة التي تتسبب في تذبذب الجسم. توجد علامة الطرح على مكون الوزن الذي يوفر قوة الاستعادة لأن القوة تعمل في الاتجاه المعاكس لزاوية الزيادة$\theta$.

عندما يتدلى البندول المادي من نقطة ما ولكنه حر في الدوران، فإنه يدور بسبب عزم الدوران المطبق على CM، الناتج عن مكون وزن الجسم الذي يعمل مماسًا لحركة CM. إذا أخذنا الاتجاه المعاكس لعقارب الساعة ليكون موجبًا، فإن مكون قوة الجاذبية التي تعمل على المماس للحركة هو −mg sin$\theta$. علامة الطرح هي نتيجة قوة الاستعادة التي تعمل في الاتجاه المعاكس للزاوية المتزايدة. تذكر أن عزم الدوران يساوي$\vec{\tau} = \vec{r} \times \vec{F}$. حجم عزم الدوران يساوي طول ذراع نصف القطر مضروبًا في المكون العرضي للقوة المطبقة، |$\tau$ | = RFSin$\theta$. هنا، طول L من ذراع نصف القطر هو المسافة بين نقطة الدوران و CM. لتحليل الحركة، ابدأ بعزم الدوران الصافي. مثل البندول البسيط، فكر في الزوايا الصغيرة فقط بحيث تكون الخطيئة$\theta$ ≈$\theta$. تذكر من دوران المحور الثابت عند الدوران أن عزم الدوران الصافي يساوي لحظة القصور الذاتي I =$\int$ r ² dm مضروبًا في التسارع الزاوي$\alpha$، حيث\ (\ ألفا =\ frac {d^ {2}\ theta} {dt^ {2} {dt^ {2}}:

\[I \alpha = \tau_{net} = L (-mg) \sin \theta \ldotp\]

استخدام تقريب الزاوية الصغيرة وإعادة ترتيبها:

\[\begin{split} I \alpha & = -L (mg) \theta; \\ I \frac{d^{2} \theta}{dt^{2}} & = -L (mg) \theta; \\ \frac{d^{2} \theta}{dt^{2}} & = - \left(\dfrac{mgL}{I}\right) \theta \ldotp \end{split}\]

مرة أخرى، تقول المعادلة أن المشتق للمرة الثانية للموضع (في هذه الحالة، الزاوية) يساوي ناقص ثابت$\left(− \dfrac{mgL}{I}\right)$ مضروبًا في الموضع. الحل هو

\[\theta (t) = \Theta \cos (\omega t + \phi),\]

أين$\Theta$ هو الحد الأقصى للنزوح الزاوي. التردد الزاوي هو

\[\omega = \sqrt{\frac{mgL}{I}} \ldotp \label{15.20}\]

وبالتالي فإن الفترة هي

\[T = 2 \pi \sqrt{\frac{I}{mgL}} \ldotp \label{15.21}\]

لاحظ أنه بالنسبة للبندول البسيط، فإن لحظة القصور الذاتي هي I =$\int$ r ² dm = ^{mL 2} وتنخفض الفترة إلى T = 2$\pi \sqrt{\frac{L}{g}}$.

مثال$\PageIndex{2}$: Reducing the Swaying of a Skyscraper

في الظروف القاسية، يمكن لناطحات السحاب التأرجح حتى مترين بتردد يصل إلى 20.00 هرتز بسبب الرياح العاتية أو النشاط الزلزالي. قامت العديد من الشركات بتطوير البندولات المادية التي يتم وضعها على قمة ناطحات السحاب. عندما تتأرجح ناطحة السحاب إلى اليمين، يتأرجح البندول إلى اليسار، مما يقلل من التأثير. بافتراض أن التذبذبات لها تردد 0.50 هرتز، صمم بندولًا يتكون من شعاع طويل ذي كثافة ثابتة وكتلته 100 طن متري ونقطة محورية في أحد طرفي الشعاع. ماذا يجب أن يكون طول الشعاع؟

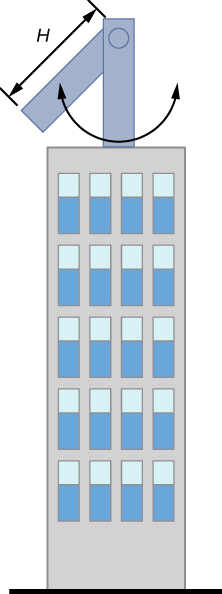
يُصوِّر الشكل مبنى طويلًا مع عمود على سقفه وقضيب طويل طوله H يتأرجح على نقطة محورية بالقرب من الجزء العلوي من العمود.

إستراتيجية

يُطلب منا إيجاد طول البندول المادي بكتلة معروفة. نحتاج أولاً إلى إيجاد لحظة القصور الذاتي للشعاع. يمكننا بعد ذلك استخدام معادلة فترة البندول المادي لإيجاد الطول.

الحل

ابحث عن لحظة القصور الذاتي لـ CM.
استخدم نظرية المحور المتوازي لإيجاد لحظة القصور الذاتي حول نقطة الدوران: $I = I_ {CM} +\ frac {L^ {2}} {4} M =\ frac {1} {1} {12} ML^ {2} +\ فراك {1} {4} ML^ {2} =\ فراك {1} {3} ML^ {2}\ ldotp$$
فترة البندول المادي لها فترة T = 2$\pi \sqrt{\frac{I}{mgL}}$. استخدم لحظة القصور الذاتي لحل الطول L: $$\ ابدأ {الانقسام} T & = 2\ pi\ sqrt {\ frac {I} {mgL} = 2\ pi\ sqrt {\ frac {\ frac {1} {3} ML^ {2}} {mGL} = 2\ pi\ sqrt {\ frac {\ frac {\ 3g}؛\ L = 3g\ يسار (\ dfrac {T} {2\ pi}\ يمين) ^ {2} = 3 (9.8\؛ م/s^ {2})\ يسار (\ dfrac {2\; s} {2\ pi}\ يمين) ^ {2} = 2.98\; m\ ldotp\ end {{2} الانقسام} $$
يمتد هذا الطول L من مركز الكتلة إلى محور الدوران، وهو نصف طول البندول. لذلك فإن طول H للبندول هو: $H = 2L = 5.96\: m $$

الدلالة

هناك العديد من الطرق لتقليل التذبذبات، بما في ذلك تعديل شكل ناطحات السحاب، واستخدام البندولات المادية المتعددة، واستخدام مخمدات الكتلة المضبوطة.

البندول الالتوائي

يتكون البندول الالتوائي من جسم صلب معلق بسلك خفيف أو زنبرك (الشكل$\PageIndex{3}$). عندما يكون الجسم ملتويًا بزاوية قصوى صغيرة ($\Theta$) ويتم تحريره من السكون، يتأرجح الجسم بين ($\theta$= +$\Theta$) و ($\theta$= −$\Theta$). يتم توفير عزم الاستعادة عن طريق قص الخيط أو السلك.

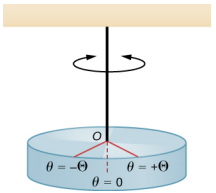
يمكن تصميم عزم الاستعادة على أنه يتناسب مع الزاوية:

\[\tau = - \kappa \theta \ldotp\]

يُعرف المتغير kappa ($\kappa$) باسم ثابت الالتواء للسلك أو السلسلة. تُظهر علامة الطرح أن عزم الاستعادة يعمل في الاتجاه المعاكس لزيادة الإزاحة الزاوية. عزم الدوران الصافي يساوي لحظة القصور الذاتي مضروبًا في التسارع الزاوي:

\[\begin{split} I \frac{d^{2} \theta}{dt^{2}} & = - \kappa \theta; \\ \frac{d^{2} \theta}{dt^{2}} & = - \frac{\kappa}{I} \theta \ldotp \end{split}\]

تشير هذه المعادلة إلى أن المشتق الزمني الثاني للموضع (في هذه الحالة، الزاوية) يساوي ثابتًا سالبًا مضروبًا في الموضع. يبدو هذا مشابهًا جدًا لمعادلة الحركة لـ SHM$\frac{d^{2} x}{dt^{2}}$ = −$\frac{k}{m}$ x، حيث وُجد أن الفترة هي T = 2$\pi \sqrt{\frac{m}{k}}$. لذلك، يمكن العثور على فترة البندول الالتوائي باستخدام

\[T = 2 \pi \sqrt{\frac{I}{\kappa}} \ldotp \label{15.22}\]

^{وحدات ثابت الالتواء هي [$\kappa$] = N • m = (كجم • m/s ²) m = kg • m 2/s ² ووحدات لحظة القصور الذاتي هي [I] = kg • m ²، مما يدل على أن وحدة الفترة هي الثانية.}

مثال$\PageIndex{3}$: Measuring the Torsion Constant of a String

طول القضيب l = 0.30 m وكتلته 4.00 kg. يتم توصيل الخيط بـ CM الخاص بالقضيب ويتم تعليق النظام من السقف (الشكل$\PageIndex{4}$). يتم إزاحة القضيب بمقدار 10 درجات عن وضع التوازن ويتم تحريره من السكون. يتذبذب القضيب بمدّة 0.5 ثانية. ما هو ثابت الالتواء$\kappa$؟

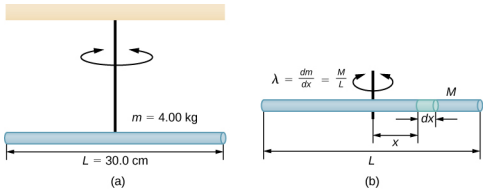
يوضِّح الشكل أ قضيبًا أفقيًا طوله ٣٠٫٠ سنتيمترًا وكتلته ٤٫٠٠ كيلوجرامًا، مُعلَّقًا بخيط من السقف. يتم ربط السلسلة بمنتصف القضيب. يدور القضيب مع الخيط في المستوى الأفقي. يوضح الشكل (ب) القضيب بالتفاصيل اللازمة للعثور على لحظة القصور الذاتي. طول القضيب، من طرف إلى طرف، هو L وكتلته الإجمالية هي M. وله كثافة كتلة خطية lambda تساوي d m d x والتي تساوي أيضًا M على L. تم تمييز جزء صغير من القضيب بطول d x على مسافة x من مركز القضيب. يتم توصيل الخيط بالقضيب الموجود في وسط القضيب. — الشكل$\PageIndex{4}$ - (أ) قضيب معلق بخيط من السقف. (ب) تحديد لحظة القصور الذاتي للقضيب.

إستراتيجية

يُطلب منا العثور على ثابت الالتواء للخيط. نحتاج أولاً إلى إيجاد لحظة القصور الذاتي.

الحل

ابحث عن لحظة القصور الذاتي لـ CM: $I_ {CM} =\ int x^ {2} dm =\ int_ {-\ frac {L} {2}} ^ {+\ frac {L} {2}} x^ {2}\ لامدا دي إكس =\ لامدا\ بيغ [\ فراك {س ^ {3}} {3}\ بيج] _ {-\ فراك {} {2}} ^ {+\ فراك {L} {2} =\ لامدا\ فراك {2L^ {3}} {24} =\ يسار (\ dfrac {M} {L}\ يمين)\ فراك {2L^ {3}} {24} =\ فراك {1} {12} مل ^ {2}\ ldo$tp$
احسب ثابت الالتواء باستخدام المعادلة للفترة: $$\ ابدأ {الانقسام} T & = 2\ pi\ sqrt {\ frac {\ frac {\ kappa}}؛\\\ كابا = أنا\ يسار (\ dfrac {2\ pi} {T}\\ اليمين) ^ {2} =\ يسار (\ dfrac {1} {12} ML^ {2}\ اليمين)\ يسار (\ dfrac {2\ pi} {T}\ يمين) ^ {2}؛\\ & =\ كبير [\ فراك {1} {12} (4.00\؛ كجم) (0.30\؛ م) ^ {2}\ كبير]\ يسار (\ dfrac {2\ pi} {0.50\; s}\ يمين) ^ {2} = 4.73\; N\;\ cdotp\ ldotp\ end {الانقسام} $$

الدلالة

مثل ثابت القوة لنظام الكتلة والزنبرك، كلما زاد ثابت الالتواء، كانت الفترة أقصر.

مثال\(\PageIndex{1}\): Measuring Acceleration due to Gravity by the Period of a Pendulum

الحل

التمارين\(\PageIndex{1}\)

مثال\(\PageIndex{2}\): Reducing the Swaying of a Skyscraper

الحل

مثال\(\PageIndex{3}\): Measuring the Torsion Constant of a String

الحل