15.4: مقارنة الحركة التوافقية البسيطة والحركة الدائرية

Last updated
Save as PDF

Page ID: 200098

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

أهداف التعلم

وصف كيفية ارتباط دوال الجيب وجيب التمام بمفاهيم الحركة الدائرية
وصف العلاقة بين الحركة التوافقية البسيطة والحركة الدائرية

طريقة سهلة لنمذجة الحركة التوافقية البسيطة (SHM) هي التفكير في الحركة الدائرية المنتظمة. \(\PageIndex{1}\)يوضح الشكل إحدى طرق استخدام هذه الطريقة. يتم توصيل الوتد (أسطوانة من الخشب) بقرص عمودي يدور بتردد زاوي ثابت.

رسم توضيحي للطريقة التي تمت مناقشتها في النص لإلقاء ظل متذبذب. يبرز الوتد من قرص دوار عمودي مثبت عموديًا على الحائط. تضيء مجموعة من الأضواء لتضيء الوتد من الأعلى. يظهر ظل الوتد أدناه كما يظهر عدة مرات أثناء التذبذب، مكونًا سلسلة من النقاط على طول خط موازٍ للجدار. المسافة من مركز الخط إلى موقع الظل هي x. — الشكل\(\PageIndex{1}\): يمكن تصميم SHM كحركة دورانية من خلال النظر إلى ظل الوتد على عجلة تدور بتردد زاوي ثابت.

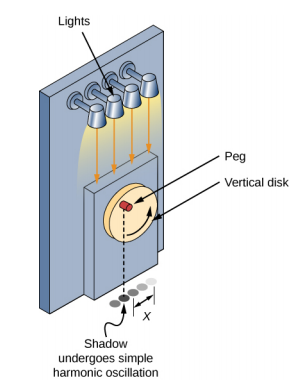
\(\PageIndex{2}\)يعرض الشكل عرضًا جانبيًا للقرص والوتد. في حالة وضع مصباح فوق القرص والوتد، ينتج الوتد ظلًا. دع نصف قطر القرص r = A وحدد موضع الظل الذي يتزامن مع الخط المركزي للقرص ليكون x = 0.00 m. وبينما يدور القرص بمعدل ثابت، يتأرجح الظل بين x = + A و x = −A. تخيل الآن كتلة على زنبرك تحت الأرض كما هو موضح في الشكل\(\PageIndex{2}\).

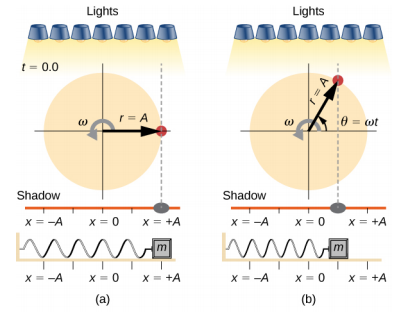
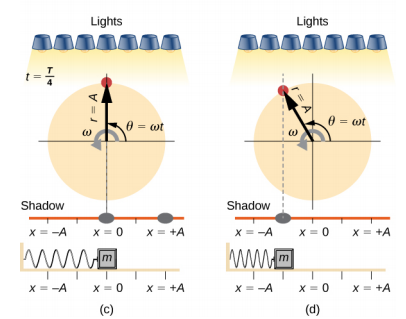
مقارنة بين الموقع الزاوي للربط على قرص دوار وموضع ظله وموضع الكتلة المتذبذبة على زنبرك أفقي. في كل شكل، يتم إضاءة الوتد من الأعلى بمجموعة من الأضواء، مما يلقي بظلاله على خط أفقي. يحتوي القرص على نصف قطر r = A ويدور عكس اتجاه عقارب الساعة بسرعة زاوية أوميغا. يكون الموضع الزاوي للشد، ثيتا، صفرًا عندما يكون الوتد مباشرةً على يمين مركز القرص. الزنبرك متصل بجدار على اليسار وكتلة على اليمين. موضع الكتلة والظل هو x، حيث يكون x=0 أسفل مركز القرص مباشرةً، و x=-a أسفل الحافة اليسرى من القرص مباشرةً، و x=+A أسفل الحافة اليمنى من القرص مباشرةً. في الشكل أ، t=0.0. يتم وضع الوتد مباشرة على يمين مركز القرص. يكون كل من ظله وكتلته عند x = +A. في الشكل ب، يكون الوتد بزاوية ثيتا يساوي أوميغا t، في الربع الأول. يقع كل من ظله وكتلته أسفل الوتد مباشرة عند ما يبدو أنه x = +A/2. لم يتم تحديد الوقت. في الشكل ج، T=T/4. يقع الوتد مباشرة فوق مركز القرص. موضعه الزاوي ثيتا يساوي أوميغا t، وظله وكتلته كلاهما عند x =0. في الشكل d، يكون الوتد بزاوية ثيتا يساوي أوميغا t، والآن في الربع الثاني. يقع كل من ظله وكتلته أسفل الوتد مباشرة عند ما يبدو أنه x = -A/2. لم يتم تحديد الوقت. — الشكل\(\PageIndex{2}\): يضيء الضوء على القرص بحيث يصنع الوتد ظلًا. إذا كان القرص يدور بالتردد الزاوي الأيمن فقط، فإن الظل يتبع حركة الكتلة على الزنبرك. إذا لم تتبدد الطاقة بسبب القوى غير المحافظة، فسوف تتأرجح الكتلة والظل ذهابًا وإيابًا في انسجام تام. في هذا الشكل، يتم التقاط أربع لقطات في أربع أوقات مختلفة. (أ) تبدأ العجلة عند\(\theta\) = 0 درجة ويكون ظل الوتد عند x = + A، ويمثل الكتلة في الموضع x = + A. (ب) عندما يدور القرص بزاوية\(\theta\) =\(\omega\) t، يكون ظل الوتد بين x = + A و x = 0. (ج) يستمر القرص في الدوران حتى\(\theta\) = 90 درجة، حيث يتبع الظل الكتلة إلى x = 0. (د) يستمر القرص في الدوران، ويتبع الظل موضع الكتلة.

إذا استدار القرص بالتردد الزاوي المناسب، يتبع الظل الكتلة. يمكن نمذجة موضع الظل بالمعادلة

\[x(t) = A \cos (\omega t) \ldotp \label{15.14}\]

تذكر أن الكتلة المتصلة بالزنبرك لا تتحرك بسرعة ثابتة. كم مرة يجب أن تدور العجلة حتى يكون ظل الوتد دائمًا على الكتلة؟ يجب أن يدور القرص بتردد زاوي ثابت يساوي\(\pi\) ضعف تردد التذبذب (\(\omega\)= 2\(\pi\) f).

\(\PageIndex{3}\)يوضح الشكل العلاقة الأساسية بين الحركة الدائرية المنتظمة و SHM. يقع الوتد في طرف نصف القطر، على مسافة A من مركز القرص. يتم تعريف المحور السيني بخط مرسوم بالتوازي مع الأرض، مما يؤدي إلى قطع القرص إلى النصف. يتم تعريف المحور y (غير الموضح) بخط عمودي على الأرض، مما يؤدي إلى قطع القرص إلى النصف الأيسر والنصف الأيمن. مركز القرص هو النقطة (x = 0، y = 0). يعطي إسقاط موضع الوتد على المحور السيني الثابت موضع الظل، الذي يخضع لـ SHM مشابهًا لنظام الكتلة والزنبرك. في الوقت الموضح في الشكل، يكون للإسقاط الموضع x ويتحرك إلى اليسار بسرعة\(v\). السرعة العرضية للربط حول الدائرة تساوي الكتلة\(\bar{v}_{max}\) الموجودة على الزنبرك. يساوي المكون x للسرعة سرعة الكتلة على الزنبرك.

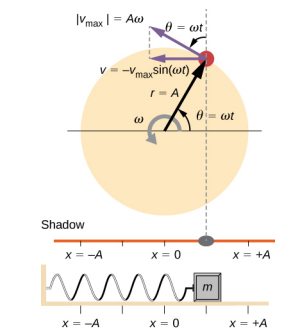
مقارنة بين الموقع الزاوي للربط على قرص دوار وموضع ظله وموضع الكتلة المتذبذبة على زنبرك أفقي. يحتوي القرص على نصف قطر r = A ويدور عكس اتجاه عقارب الساعة بسرعة زاوية أوميغا. يكون الموضع الزاوي للشد، ثيتا، صفرًا عندما يكون الوتد على يمين مركز القرص مباشرةً ويساوي أوميجا t في الوقت الموضح. تظهر السرعة الخطية للربط في صورة مماس متجه للدائرة عند حافة القرص. يبلغ حجمه v sub-max وهو يساوي A omega. مكون x الخاص به هو متجه أفقي يساري - v دون الحد الأقصى للأوقات منذ أوميغا t. يلقي الوتد ظلًا على خط أفقي. الزنبرك متصل بجدار على اليسار وكتلة على اليمين. موضع الكتلة والظل هو x، حيث يكون x=0 أسفل مركز القرص مباشرةً، و x=-a أسفل الحافة اليسرى من القرص مباشرةً، و x=+A أسفل الحافة اليمنى من القرص مباشرةً. في الشكل، يكون الوتد في الربع الأول. يقع كل من ظله وكتلته في موضع x بين 0 وزائد A (يبدو أنه في x = A/2 في الشكل.) — الشكل\(\PageIndex{3}\): - الوتد الذي يتحرك على مسار دائري بسرعة زاوية ثابتة Ω يخضع لحركة دائرية منتظمة. يخضع إسقاطه على المحور السيني لـ SHM. كما تظهر أيضًا سرعة الوتد حول الدائرة، و v _max، وإسقاطه، وهو v. لاحظ أن هذه السرعات تشكل مثلثًا مشابهًا لمثلث الإزاحة.

يمكننا استخدام الشكل\(\PageIndex{3}\) لتحليل سرعة الظل أثناء تدوير القرص. يتحرك الوتد في دائرة بسرعة v _max = A\(\omega\). يتحرك الظل بسرعة تساوي مكون سرعة الوتد الموازي للسطح حيث يتم إنتاج الظل:

\[v = -v_{max} \sin (\omega t) \ldotp \label{15.15}\]

ويترتب على ذلك أن التسارع هو

\[a = -a_{max} \cos (\omega t) \ldotp \label{15.16}\]

التمرين 15.3

حدد كائنًا يخضع لحركة دائرية منتظمة. وصف كيف يمكنك تتبع SHM لهذا الكائن.