15.3: الطاقة في الحركة التوافقية البسيطة
- Page ID
- 200091
- وصف الحفاظ على الطاقة في نظام الكتلة والنبع
- شرح مفاهيم نقاط التوازن المستقرة وغير المستقرة
لإنتاج تشوه في كائن ما، يجب علينا القيام بالعمل. أي أنه سواء كنت تقطف خيطًا للجيتار أو تضغط على ممتص الصدمات في السيارة، يجب ممارسة القوة عبر مسافة. إذا كانت النتيجة الوحيدة هي التشوه، ولم ينتقل أي عمل إلى الطاقة الحرارية أو الصوتية أو الحركية، فسيتم تخزين كل العمل مبدئيًا في الجسم المشوه كشكل من أشكال الطاقة الكامنة.
خذ بعين الاعتبار مثال كتلة متصلة بنابض على طاولة خالية من الاحتكاك تتأرجح في SHM. قوة الربيع هي قوة محافظة (درستها في الفصل الخاص بالطاقة المحتملة والحفاظ على الطاقة)، ويمكننا تحديد الطاقة المحتملة لها. هذه الطاقة الكامنة هي الطاقة المخزنة في الربيع عندما يتم تمديد الزنبرك أو ضغطه. في هذه الحالة، تتأرجح الكتلة في بُعد واحد مع قوة الزنبرك التي تعمل بالتوازي مع الحركة:
\[W = \int_{x_{i}}^{x_{f}} F_{x} dx \int_{x_{i}}^{x_{f}} -kxdx = \Big[ - \frac{1}{2} kx^{2} \Big]_{x_{i}}^{x_{f}} = - \Big[ \frac{1}{2} kx_{f}^{2} - \frac{1}{2} kx_{i}^{2} \Big] = - [U_{f} - U_{i}] = - \Delta U \ldotp\]
عند النظر إلى الطاقة المخزنة في الزنبرك، فإن موضع التوازن، المحدد بـ x i = 0.00 m، هو الموضع الذي تكون فيه الطاقة المخزنة في الزنبرك مساوية للصفر. عندما يتم تمديد الزنبرك أو ضغطه بمسافة x، تكون الطاقة الكامنة المخزنة في الربيع
\[U = \frac{1}{2} kx^{2} \ldotp\]
الطاقة والمذبذب التوافقي البسيط
لدراسة طاقة المذبذب التوافقي البسيط، نحتاج إلى النظر في جميع أشكال الطاقة. خذ بعين الاعتبار مثال كتلة متصلة بنابض، موضوعة على سطح خالٍ من الاحتكاك، تتأرجح في SHM. الطاقة الكامنة المخزنة في تشوه الربيع هي
\[U = \frac{1}{2} kx^{2} \ldotp\]
في مذبذب توافقي بسيط، تتأرجح الطاقة بين الطاقة الحركية للكتلة K =\(\frac{1}{2}\) mv 2 والطاقة الكامنة U =\(\frac{1}{2}\) kx 2 المخزنة في الزنبرك. في SHM لنظام الكتلة والربيع، لا توجد قوى تبديد، وبالتالي فإن الطاقة الكلية هي مجموع الطاقة الكامنة والطاقة الحركية. في هذا القسم، ننظر في الحفاظ على طاقة النظام. المفاهيم التي تم فحصها صالحة لجميع المذبذبات التوافقية البسيطة، بما في ذلك تلك التي تلعب فيها قوة الجاذبية دورًا.
ضع في اعتبارك الشكل\(\PageIndex{1}\) الذي يُظهر كتلة متذبذبة متصلة بنابض. في حالة SHM غير المثبط، تتأرجح الطاقة ذهابًا وإيابًا بين الحركية والإمكانات، وتنتقل تمامًا من شكل من أشكال الطاقة إلى الآخر أثناء تذبذب النظام. لذلك بالنسبة للمثال البسيط لجسم على سطح غير قابل للاحتكاك متصل بنابض، تبدأ الحركة بكل الطاقة المخزنة في الزنبرك كطاقة كامنة مرنة. عندما يبدأ الجسم في التحرك، يتم تحويل الطاقة الكامنة المرنة إلى طاقة حركية، لتصبح طاقة حركية بالكامل في موضع التوازن. ثم يتم تحويل الطاقة مرة أخرى إلى طاقة كامنة مرنة بحلول الزنبرك أثناء تمديده أو ضغطه. تصبح السرعة صفرًا عندما يتم تحويل الطاقة الحركية بالكامل، ثم تتكرر هذه الدورة. إن فهم الحفاظ على الطاقة في هذه الدورات سيوفر رؤية إضافية هنا وفي التطبيقات اللاحقة لـ SHM، مثل الدوائر المتناوبة.
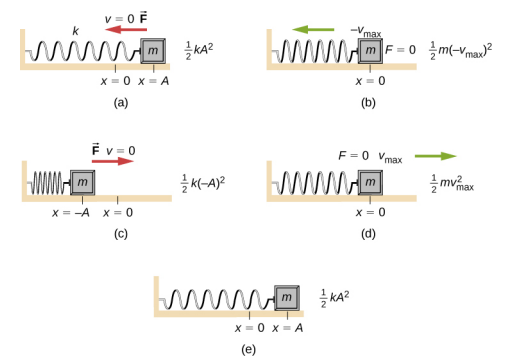
ضع في اعتبارك الشكل\(\PageIndex{1}\) الذي يوضح الطاقة في نقاط محددة من الحركة الدورية. مع الحفاظ على ثباتها، تتأرجح الطاقة بين الطاقة الحركية للكتلة والطاقة الكامنة المخزنة في الزنبرك:
\[E_{Total} = U + K = \frac{1}{2} kx^{2} + \frac{1}{2} mv^{2} \ldotp\]
يتم تحديد حركة الكتلة على الزنبرك في SHM من خلال الموضع x (t) = Acos\(\omega\) t +\(\phi\)) بسرعة v (t) = −A\(\omega\) sin (\(\omega\)t +\(\phi\)). باستخدام هذه المعادلات، تكون الهوية المثلثية cos 2\(\theta\) + sin 2\(\theta\) = 1\(\omega = \sqrt{\frac{k}{m}}\)، ويمكننا إيجاد الطاقة الكلية للنظام:
\[\begin{split} E_{Total} & = \frac{1}{2} kA^{2} \cos^{2} (\omega t + \phi) + \frac{1}{2} mA^{2} \omega^{2} \sin^{2} (\omega t + \phi) \\ & = \frac{1}{2} kA^{2} \cos^{2} (\omega t + \phi) + \frac{1}{2} mA^{2} \left(\dfrac{k}{m}\right) \sin^{2} (\omega t + \phi) \\ & = \frac{1}{2} kA^{2} \cos^{2} (\omega t + \phi) + \frac{1}{2} kA^{2} \sin^{2} (\omega t + \phi) \\ & = \frac{1}{2} kA^{2} \cos^{2} (\omega t + \phi) + \frac{1}{2} mA^{2} \omega^{2} \sin^{2} (\omega t + \phi) \\ & = \frac{1}{2} kA^{2} (\cos^{2} (\omega t + \phi) + \sin^{2} (\omega t + \phi)) \\ & = \frac{1}{2} kA^{2} \ldotp \end{split}\]
الطاقة الكلية لنظام الكتلة والزنبرك تساوي مجموع الطاقة الكامنة المخزنة في الزنبرك بالإضافة إلى الطاقة الحركية للكتلة وتتناسب مع مربع السعة E Total =\(\left(\dfrac{1}{2}\right)\) kA 2. الطاقة الإجمالية للنظام ثابتة.
يُظهر إلقاء نظرة فاحصة على طاقة النظام أن الطاقة الحركية تتأرجح مثل دالة جيبية التربيعية، بينما تتأرجح الطاقة الكامنة مثل دالة مربع جيب التمام. ومع ذلك، فإن الطاقة الكلية للنظام ثابتة وتتناسب مع مربع السعة. \(\PageIndex{2}\)يوضِّح الشكل مخططًا للطاقات الكامنة والحركية والإجمالية لنظام الكتلة والنابض كدالة للوقت. يتم أيضًا رسم الموضع والسرعة كدالة للوقت. قبل الوقت t = 0.0 ثانية، يتم ربط الكتلة بالزنبرك ووضعها في موضع التوازن. يتم العمل على الكتلة من خلال تطبيق قوة خارجية، وسحبها إلى موضع x = + A. يحتوي النظام الآن على طاقة كامنة مخزنة في الزنبرك. في الوقت t = 0.00 ثانية، يكون موضع الكتلة مساويًا للسعة، والطاقة الكامنة المخزنة في الزنبرك تساوي U =\(\frac{1}{2}\) kA 2، والقوة على الكتلة هي القصوى وتشير في الاتجاه السيني السالب (F S = −kA). تكون سرعة الكتلة وطاقتها الحركية صفرًا في الوقت t = 0.00 ثانية، وفي الوقت t = 0.00 ثانية، يتم تحرير الكتلة من السكون.
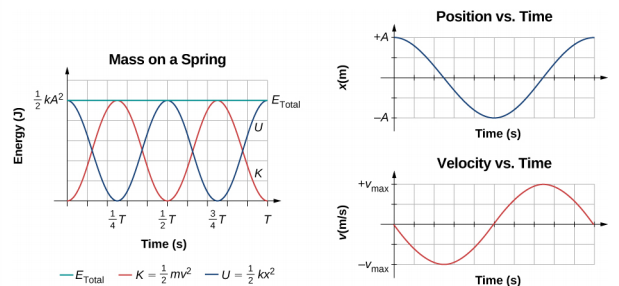
تذبذبات حول موضع التوازن
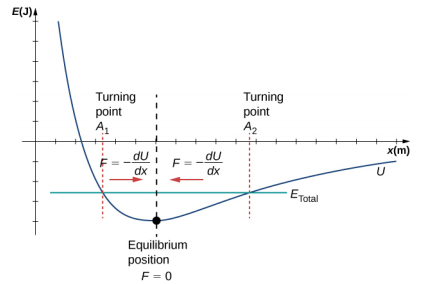
لقد نظرنا للتو في طاقة SHM كدالة للوقت. وجهة نظر أخرى مثيرة للاهتمام للمذبذب التوافقي البسيط هي اعتبار الطاقة كدالة للموضع. \(\PageIndex{3}\)يوضح الشكل رسمًا بيانيًا للطاقة مقابل موضع النظام الذي يخضع لـ SHM.
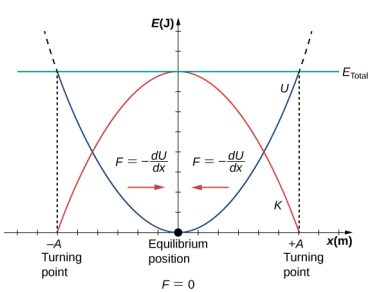
\(\PageIndex{3}\)يشبه منحنى الطاقة الكامنة في الشكل وعاءًا. عندما يتم وضع الرخام في وعاء، فإنه يستقر في وضع التوازن عند أدنى نقطة من الوعاء (x = 0). يحدث هذا لأن قوة الاستعادة تشير إلى نقطة التوازن. يشار إلى نقطة التوازن هذه أحيانًا كنقطة ثابتة. عندما يتم تحريك الرخام إلى موضع مختلف (x = + A)، يتأرجح الرخام حول موضع التوازن. بالنظر إلى الرسم البياني للطاقة الكامنة، يمكن العثور على القوة من خلال النظر إلى منحدر الرسم البياني للطاقة الكامنة (F = −\(\frac{dU}{dx}\)). نظرًا لأن القوة الموجودة على جانبي النقطة الثابتة تشير إلى نقطة التوازن، فإن نقطة التوازن تسمى نقطة توازن مستقرة. تسمى النقاط x = A و x = −A نقاط التحول. (انظر الطاقة المحتملة والحفاظ على الطاقة.) الاستقرار مفهوم مهم. إذا كانت نقطة التوازن مستقرة، فإن الاضطراب الطفيف لجسم يكون في البداية عند نقطة التوازن المستقرة سيؤدي إلى تذبذب الجسم حول تلك النقطة. تحدث نقطة التوازن المستقرة لأن القوة على كلا الجانبين موجهة نحوها. بالنسبة لنقطة توازن غير مستقرة، إذا كان الكائن مضطربًا قليلاً، فإنه لا يعود إلى نقطة التوازن.
خذ بعين الاعتبار مثال الرخام الموجود في الوعاء. إذا كان الوعاء في الجانب الأيمن لأعلى، فإن الرخام، إذا تم إزعاجه قليلاً، سوف يتذبذب حول نقطة التوازن المستقرة. إذا انقلب الوعاء رأسًا على عقب، يمكن موازنة الرخام في الأعلى، عند نقطة التوازن حيث تكون القوة الصافية صفرًا. ومع ذلك، إذا تم إزعاج الرخام قليلاً، فلن يعود إلى نقطة التوازن، ولكنه سيتدحرج بدلاً من ذلك من الوعاء. والسبب هو أن القوة على جانبي نقطة التوازن موجهة بعيدًا عن تلك النقطة. هذه النقطة هي نقطة توازن غير مستقرة.
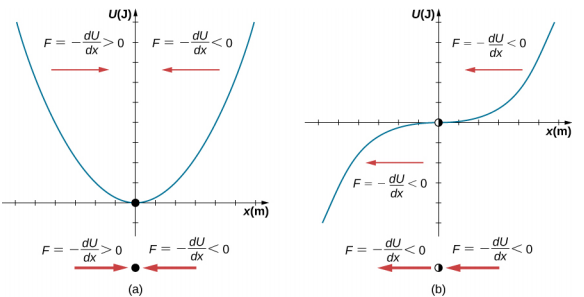
\(\PageIndex{4}\)يوضح الشكل ثلاثة شروط. الأولى هي نقطة توازن مستقرة (أ)، والثانية هي نقطة توازن غير مستقرة (b)، والأخيرة هي أيضًا نقطة توازن غير مستقرة (c)، لأن القوة على جانب واحد فقط تشير إلى نقطة التوازن.
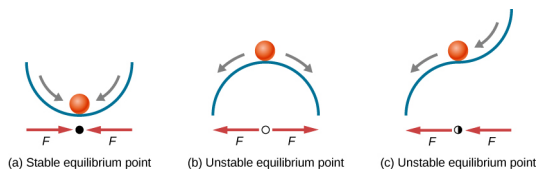
يمكن إضفاء الطابع الرسمي على عملية تحديد ما إذا كانت نقطة التوازن مستقرة أم غير مستقرة. ضع في اعتبارك منحنيات الطاقة المحتملة الموضحة في الشكل\(\PageIndex{5}\). يمكن العثور على القوة من خلال تحليل منحدر الرسم البياني. القوة هي F = −\(\frac{dU}{dx}\). في (أ)، تكون النقطة الثابتة عند x = 0.00 m، وعندما تكون x < 0.00 m، تكون القوة موجبة. عندما تكون x > 0.00 م، تكون القوة سالبة. هذه نقطة مستقرة. في (ب)، تكون النقطة الثابتة عند x = 0.00 m، وعندما تكون x < 0.00 m، تكون القوة سالبة. عندما تكون x > 0.00 م، تكون القوة سالبة أيضًا. هذه نقطة غير مستقرة.
التطبيق العملي لمفهوم نقاط التوازن المستقرة هو القوة بين ذرتين محايدتين في الجزيء. إذا كان هناك جزيئان على مقربة، يفصل بينهما بضعة أقطار ذرية، فيمكنهما تجربة قوة جذابة. إذا اقتربت الجزيئات بدرجة كافية بحيث تتداخل الأصداف الإلكترونية للإلكترونات الأخرى، تصبح القوة بين الجزيئات مثيرة للاشمئزاز. قد تتسبب قوة الجذب بين الذرتين في تكوين الذرات لجزيء. القوة بين الجزيئين ليست قوة خطية ولا يمكن تشكيلها ببساطة على شكل كتلتين يفصل بينهما زنبرك، لكن ذرات الجزيء يمكن أن تتأرجح حول نقطة توازن عند إزاحة كمية صغيرة من موضع التوازن. تتأرجح الذرات بسبب القوة الجذابة والقوة الطاردة بين الذرتين.
لنأخذ مثالاً واحدًا للتفاعل بين ذرتين يُعرف باسم تفاعل van Der Waals. يقع خارج نطاق هذا الفصل مناقشة التفاعلات بين الذرتين بعمق، ولكن يمكن فحص تذبذبات الذرات من خلال النظر في مثال واحد لنموذج الطاقة الكامنة للنظام. أحد الاقتراحات لنمذجة الطاقة الكامنة لهذا الجزيء هو باستخدام إمكانات Lennard-Jones 6-12:
\[U(x) = 4 \epsilon \Bigg[ \left(\dfrac{\sigma}{x}\right)^{12} - \left(\dfrac{\sigma}{x}\right)^{6} \Bigg] \ldotp\]
يظهر الرسم البياني لهذه الدالة في الشكل\(\PageIndex{6}\). تم العثور\(\epsilon\) على\(\sigma\) المعلمتين بشكل تجريبي.
من الرسم البياني، يمكنك أن ترى أن هناك بئر طاقة محتمل، له بعض أوجه التشابه مع بئر الطاقة المحتمل لوظيفة الطاقة الكامنة للمذبذب التوافقي البسيط الذي تمت مناقشته في الشكل\(\PageIndex{3}\). يحتوي جهد Lennard-Jones على نقطة توازن مستقرة حيث تكون الطاقة الكامنة عند الحد الأدنى وتشير القوة على جانبي نقطة التوازن نحو نقطة التوازن. لاحظ أنه على عكس المذبذب التوافقي البسيط، فإن البئر المحتمل لإمكانات لينارد-جونز ليس متماثلًا. هذا يرجع إلى حقيقة أن القوة بين الذرات ليست قوة قانون هوك وليست خطية. لا تزال الذرات تتأرجح حول موضع التوازن x min لأنه عندما تكون x < x min، تكون القوة موجبة؛ عندما تكون x > x min، تكون القوة سالبة. لاحظ أنه مع اقتراب x من الصفر، يكون المنحدر حادًا وسالبًا جدًا، مما يعني أن القوة كبيرة وإيجابية. يشير هذا إلى أن محاولة دفع الذرات بالقرب من بعضها تتطلب قوة كبيرة. عندما تصبح x كبيرة بشكل متزايد، يصبح المنحدر أقل حدة والقوة أصغر وسلبية. يشير هذا إلى أنه إذا تم إعطاء طاقة كبيرة بما يكفي، يمكن فصل الذرات.
إذا كنت مهتمًا بهذا التفاعل، فأوجد القوة بين الجزيئات بأخذ مشتق دالة الطاقة الكامنة. سترى على الفور أن القوة لا تشبه قوة قانون هوك (F = −kx)، ولكن إذا كنت على دراية بنظرية ذات الحدين:
\[(1 + x)^{n} = 1 + nx + \frac{n(n - 1)}{2!} x^{2} + \frac{n(n - 1)(n - 2)}{3!} x^{3} + \cdots,\]
يمكن تقريب القوة من قبل قوة قانون هوك.
السرعة والحفاظ على الطاقة
بالعودة إلى نظام الكتلة والزنبرك في الشكل\(\PageIndex{1}\)، بمجرد تحرير الكتلة من السكون، فإنها تبدأ في التحرك في الاتجاه السلبي نحو وضع التوازن. تنخفض الطاقة الكامنة ويزداد حجم السرعة والطاقة الحركية. في الوقت t =\(\frac{T}{4}\)، تصل الكتلة إلى موضع التوازن x = 0.00 m، حيث تكون القوة على الكتلة والطاقة الكامنة صفرًا. عند وضع التوازن، تصل الكتلة إلى سرعة سالبة بحجم يساوي السرعة القصوى v = −A\(\omega\). الطاقة الحركية هي الحد الأقصى وتساوي K =\(\frac{1}{2}\) mV 2 =\(\frac{1}{2}\) mA 2 Ω\(\omega^{2}\) =\(\frac{1}{2}\) kA 2. عند هذه النقطة، تكون القوة المؤثِّرة على الكتلة صفرًا، لكن الزخم يحمل الكتلة، ويستمر في الاتجاه السالب نحو x = −A، ومع استمرار الكتلة في التحرك، تؤثِّر القوة المؤثِّرة عليها في الاتجاه الموجب ويقل مقدار السرعة والطاقة الحركية. تزداد الطاقة الكامنة مع ضغط الزنبرك. في الوقت t =\(\frac{T}{2}\)، تصل الكتلة إلى x = −A، وهنا تساوي السرعة والطاقة الحركية صفرًا. القوة على الكتلة هي F = + kA والطاقة الكامنة المخزنة في الزنبرك هي U =\(\frac{1}{2}\) kA 2. أثناء التذبذبات، تكون الطاقة الكلية ثابتة وتساوي مجموع الطاقة الكامنة والطاقة الحركية للنظام،
\[E_{Total} = \frac{1}{2} kx^{2} + \frac{1}{2} mv^{2} = \frac{1}{2} kA^{2} \ldotp \label{15.12}\]
يمكن حل معادلة الطاقة المرتبطة بـ SHM لإيجاد حجم السرعة في أي موضع:
\[|v| = \sqrt{\frac{k}{m} (A^{2} - x^{2})} \ldotp \label{15.13}\]
تتناسب الطاقة في المذبذب التوافقي البسيط مع مربع السعة. عند التفكير في العديد من أشكال التذبذبات، ستجد الطاقة المتناسبة مع مربع السعة.
لماذا ستتألم أكثر إذا قطعت يدك بمسطرة مقارنة بزنبرك سائب، حتى لو كانت إزاحة كل نظام متساوية؟
حدد إحدى الطرق التي يمكنك من خلالها تقليل السرعة القصوى لمذبذب توافقي بسيط.


