15.2: الحركة التوافقية البسيطة
- Page ID
- 200107
- حدد المصطلحات والفترة والتكرار
- ضع قائمة بخصائص الحركة التوافقية البسيطة
- شرح مفهوم التحول المرحلي
- اكتب معادلات الحركة لنظام الكتلة والزنبرك الذي يمر بحركة توافقية بسيطة
- وصف حركة كتلة تتأرجح على زنبرك عمودي
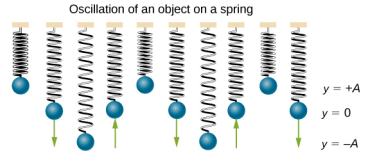
عندما تقطف سلسلة جيتار، يكون الصوت الناتج ثابتًا ويستمر لفترة طويلة (الشكل\(\PageIndex{1}\)). يهتز الخيط حول موضع التوازن، ويكتمل التذبذب عندما تبدأ السلسلة من الموضع الأولي، وتنتقل إلى أحد المواضع المتطرفة، ثم إلى الموضع المتطرف الآخر، وتعود إلى موضعها الأولي. نُعرّف الحركة الدورية بأنها أي حركة تتكرر على فترات زمنية منتظمة، مثل تلك التي تظهرها أوتار الجيتار أو طفل يتأرجح على الأرجوحة. في هذا القسم، ندرس الخصائص الأساسية للتذبذبات ووصفها الرياضي.

الفترة والتردد في التذبذبات
في حالة عدم وجود احتكاك، يظل وقت إكمال التذبذب ثابتًا ويسمى الفترة (T). عادة ما تكون وحداتها ثوانٍ، ولكنها قد تكون أي وحدة زمنية مناسبة. تشير كلمة «فترة» إلى الوقت المخصص لبعض الأحداث سواء كانت متكررة أم لا، ولكن في هذا الفصل، سنتعامل بشكل أساسي مع الحركة الدورية، وهي بطبيعتها متكررة.
المفهوم المرتبط ارتباطًا وثيقًا بالفترة هو تكرار الحدث. يُعرّف التردد (f) بأنه عدد الأحداث لكل وحدة زمنية. بالنسبة للحركة الدورية، التردد هو عدد التذبذبات لكل وحدة زمنية. العلاقة بين التردد والفترة هي
\[f = \frac{1}{T} \ldotp \label{15.1}\]
وحدة SI للتردد هي الهرتز (Hz) ويتم تعريفها على أنها دورة واحدة في الثانية:
\[1\; Hz = 1\; cycle/sec\; or\; 1\; Hz = \frac{1}{s} = 1\; s^{-1} \ldotp\]
الدورة هي تذبذب كامل
يتم استخدام أجهزة الموجات فوق الصوتية من قبل المتخصصين الطبيين لعمل صور لفحص الأعضاء الداخلية للجسم. يصدر جهاز الموجات فوق الصوتية موجات صوتية عالية التردد تنعكس على الأعضاء، ويستقبل الكمبيوتر الموجات ويستخدمها لإنشاء صورة. يمكننا استخدام الصيغ المقدمة في هذه الوحدة لتحديد التردد، بناءً على ما نعرفه عن التذبذبات. ضع في اعتبارك استخدام جهاز تصوير طبي ينتج الموجات فوق الصوتية عن طريق التذبذب بفترة 0.400\(\mu\) ثانية، فما تردد هذا التذبذب؟
إستراتيجية
يتم إعطاء الفترة (T) ويطلب منا العثور على التردد (f).
الحل
استبدل 0.400 ميكروثانية عن T في f =\(\frac{1}{T}\):
\[f = \frac{1}{T} = \frac{1}{0.400 \times 10^{-6}\; s} \ldotp \nonumber\]
حل للعثور
\[f = 2.50 \times 10^{6}\; Hz \ldotp \nonumber\]
الأهمية
تردد الصوت هذا أعلى بكثير من أعلى تردد يمكن للبشر سماعه (نطاق السمع البشري هو 20 هرتز إلى 20000 هرتز)؛ لذلك، تسمى الموجات فوق الصوتية. تؤدي التذبذبات المناسبة عند هذا التردد إلى توليد الموجات فوق الصوتية المستخدمة في التشخيصات الطبية غير الباضعة، مثل ملاحظات الجنين في الرحم.
خصائص الحركة التوافقية البسيطة
نوع شائع جدًا من الحركة الدورية يسمى الحركة التوافقية البسيطة (SHM). يُطلق على النظام الذي يتأرجح مع SHM اسم المذبذب التوافقي البسيط.
في الحركة التوافقية البسيطة، يتناسب تسارع النظام، وبالتالي القوة الصافية، مع الإزاحة ويعمل في الاتجاه المعاكس للإزاحة.
من الأمثلة الجيدة على SHM جسم كتلته\(m\) متصلة بنابض على سطح خالٍ من الاحتكاك، كما هو موضح في الشكل\(\PageIndex{2}\). يتذبذب الجسم حول موضع التوازن، والقوة الكلية على الجسم تساوي القوة التي يوفرها الزنبرك. تخضع هذه القوة لقانون هوك F s = −kx، كما تمت مناقشته في الفصل السابق.
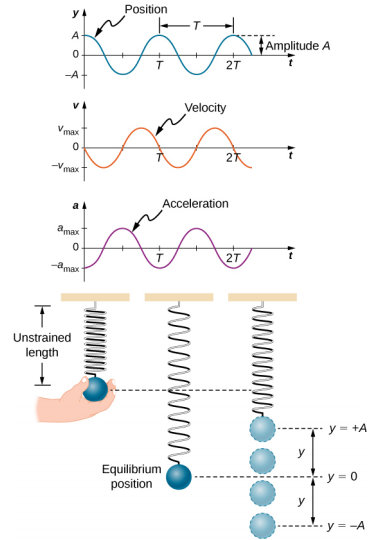
إذا كان من الممكن وصف القوة الصافية بموجب قانون هوك ولم يكن هناك أي تخميد (يتباطأ بسبب الاحتكاك أو القوى غير المحافظة الأخرى)، فإن المذبذب التوافقي البسيط يتذبذب بإزاحة متساوية على جانبي موضع التوازن، كما هو موضح لجسم على زنبرك في الشكل \(\PageIndex{2}\). الحد الأقصى للإزاحة من التوازن يسمى السعة (A). وحدات السعة والإزاحة هي نفسها ولكنها تعتمد على نوع التذبذب. بالنسبة للكائن الموجود على الزنبرك، تكون وحدات السعة والإزاحة هي الأمتار.
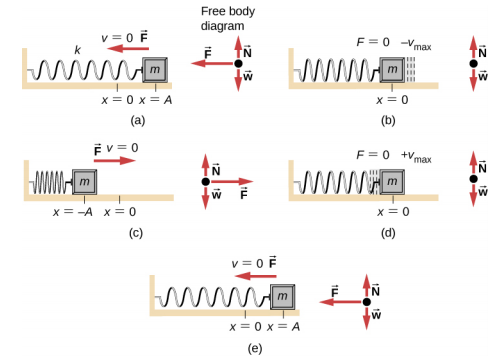
ما هو المهم جدًا في SHM؟ لسبب واحد، تكون فترة\(T\) وتردد\(f\) المذبذب التوافقي البسيط مستقلتان عن السعة. تتأرجح سلسلة الجيتار، على سبيل المثال، بنفس التردد سواء تم انتزاعها برفق أو بقوة.
هناك عاملان مهمان يؤثران على فترة المذبذب التوافقي البسيط. ترتبط الفترة بمدى صلابة النظام. يحتوي الجسم شديد الصلابة على ثابت قوة كبير (k)، مما يجعل النظام يحتوي على فترة أصغر. على سبيل المثال، يمكنك ضبط صلابة لوح الغوص - كلما كانت أكثر صلابة، زادت سرعة اهتزازه، وقلصت مدته. تعتمد الفترة أيضًا على كتلة النظام المتذبذب. كلما زاد حجم النظام، زادت الفترة. على سبيل المثال، يرتد الشخص الثقيل على لوح الغوص لأعلى ولأسفل ببطء أكثر من الشخص الخفيف. في الواقع، الكتلة m وثابت القوة k هما العاملان الوحيدان اللذان يؤثران على فترة وتواتر SHM. لاشتقاق معادلة للفترة والتردد، يجب علينا أولاً تحديد وتحليل معادلات الحركة. لاحظ أن ثابت القوة يشار إليه أحيانًا باسم ثابت الزنبرك.
معادلات SHM
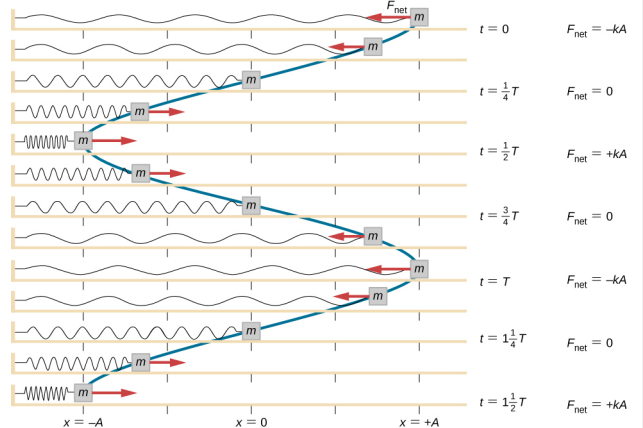
ضع في اعتبارك كتلة متصلة بنابض على طاولة خالية من الاحتكاك (الشكل\(\PageIndex{3}\)). يتم وضع علامة على موضع التوازن (الموضع الذي لا يكون فيه الزنبرك ممتدًا أو مضغوطًا) على أنه x = 0. في وضع التوازن، تكون القوة الصافية صفرًا.
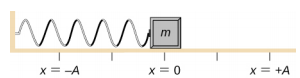
يتم العمل على الكتلة لسحبها إلى موضع x = + A، ثم يتم تحريرها من السكون. يُطلق على الحد الأقصى للموضع x (A) سعة الحركة. تبدأ الكتلة بالتذبذب في SHM بين x = + A و x = −A، حيث A هي سعة الحركة و T هي فترة التذبذب. الفترة هي الوقت المناسب لتذبذب واحد. \(\PageIndex{4}\)يوضح الشكل حركة الكتلة لأنها تكمل تذبذبًا ونصفًا بعد الإصدار.
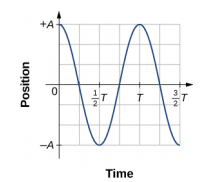
\(\PageIndex{4}\)يوضح الشكل مخططًا لموضع الكتلة مقابل الوقت. عندما يتم رسم الموضع مقابل الوقت، فمن الواضح أنه يمكن نمذجة البيانات بواسطة دالة جيب التمام بسعة\(A\) وفترة\(T\). \(\theta\)تكرر دالة جيب التمام cos كل مضاعف للعدد 2\(\pi\)، بينما تتكرر حركة الكتلة في كل فترة T. ومع ذلك، فإن الدالة\(\cos \left(\dfrac{2 \pi}{T} t \right)\) تكرر كل عدد صحيح مضاعف من الفترة. الحد الأقصى لدالة جيب التمام هو واحد، لذلك من الضروري ضرب دالة جيب التمام بالسعة A.
\[x(t) = A \cos \left(\dfrac{2 \pi}{T} t \right) = A \cos (\omega t) \ldotp \label{15.2}\]
تذكر من الفصل الخاص بالدوران أن التردد الزاوي يساوي\(\omega = \frac{d \theta}{dt}\). في هذه الحالة، تكون الفترة ثابتة، لذلك يتم تعريف التردد الزاوي على أنه 2\(\pi\) مقسومًا على الفترة،\(\omega = \frac{2 \pi}{T}\).
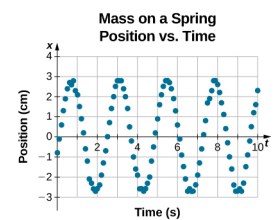
\(x(t) = A\cos( \omega t)\)تعتبر معادلة الموضع كدالة للوقت جيدة لنمذجة البيانات، حيث يكون موضع الكتلة في الوقت الأولي t = 0.00 ثانية عند السعة A والسرعة الأولية هي صفر. غالبًا عند أخذ البيانات التجريبية، لا يكون موضع الكتلة في الوقت الأولي t = 0.00 ثانية مساويًا للسعة والسرعة الأولية ليست صفرًا. خذ بعين الاعتبار 10 ثوانٍ من البيانات التي جمعها الطالب في التمرين المعملي، كما هو موضح في الشكل\(\PageIndex{6}\).
لا يزال من\(\PageIndex{6}\) الممكن تصميم البيانات في الشكل باستخدام دالة دورية، مثل دالة جيب التمام، ولكن يتم تحويل الدالة إلى اليمين. يُعرف هذا التحول باسم التحول المرحلي وعادة ما يتم تمثيله بالحرف اليوناني phi (\(\phi\)). تصبح معادلة الموضع كدالة للوقت لكتلة على زنبرك
\[x(t) = A \cos (\omega t + \phi) \ldotp\]
هذه هي المعادلة المعممة لـ SHM حيث t هو الوقت المقاس بالثواني،\(\omega\) وهو التردد الزاوي بوحدات الثواني العكسية، A هو السعة المقاسة بالأمتار أو السنتيمترات،\(\phi\) وهو التحول الطوري المقاس بالراديان (الشكل\(\PageIndex{7}\)). وتجدر الإشارة إلى أنه نظرًا لاختلاف دوال الجيب وجيب التمام فقط باختلاف الطور، يمكن نمذجة هذه الحركة باستخدام دالة جيب التمام أو الجيب.
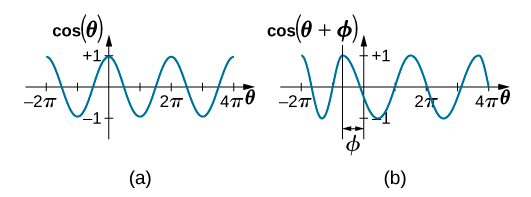
يمكن العثور على سرعة الكتلة على الزنبرك، المتذبذبة في SHM، عن طريق أخذ مشتق معادلة الموضع:
\[v(t) = \frac{dx}{dt} = \frac{d}{dt} (A \cos (\omega t + \phi)) = -A \omega \sin(\omega t + \varphi) = -v_{max} \sin (\omega t + \phi) \ldotp\]
نظرًا لأن الدالة الجيبية تتأرجح بين —1 و+1، فإن السرعة القصوى هي السعة مضروبة في التردد الزاوي، v max = A\(\omega\). تحدث السرعة القصوى في موضع التوازن (x = 0) عندما تتحرك الكتلة نحو x = + A. يتم الوصول إلى السرعة القصوى في الاتجاه السلبي عند موضع التوازن (x = 0) عندما تتحرك الكتلة نحو x = −A وتساوي −v كحد أقصى.
يمكن العثور على تسارع الكتلة على الزنبرك بأخذ المشتق الزمني للسرعة:
\[a(t) = \frac{dv}{dt} = \frac{d}{dt} (-A \omega \sin (\omega t + \phi)) = -A \omega^{2} \cos (\omega t + \varphi) = -a_{max} \cos (\omega t + \phi) \ldotp\]
الحد الأقصى للتسارع هو الحد الأقصى = A\(\omega^{2}\). يحدث التسارع الأقصى عند الموضع (x = −A)، والتسارع عند الموضع (x = −A) ويساوي −a كحد أقصى.
ملخص معادلات الحركة لـ SHM
باختصار، يمكن نمذجة الحركة التذبذبية لكتلة على زنبرك باستخدام معادلات الحركة التالية:
\[ \begin{align} x(t) &= A \cos (\omega t + \phi) \label{15.3} \\[4pt] v(t) &= -v_{max} \sin (\omega t + \phi) \label{15.4} \\[4pt] a(t) &= -a_{max} \cos (\omega t + \phi) \label{15.5} \end{align}\]
مع
\[ \begin{align} x_{max} &= A \label{15.6} \\[4pt] v_{max} &= A \omega \label{15.7} \\[4pt] a_{max} &= A \omega^{2} \ldotp \label{15.8} \end{align}\]
هنا،\(A\) هو اتساع الحركة،\(T\) هو الفترة،\(\phi\) هو التحول الطوري، و\(\omega = \frac{2 \pi}{T}\) = 2\(\pi\) f هو التردد الزاوي لحركة الكتلة.
يتم وضع كتلة بوزن 2.00 كجم على سطح غير قابل للاحتكاك. يتم تثبيت زنبرك بقوة ثابتة k = 32.00 نيوتن/م بالكتلة، والطرف المقابل من الزنبرك متصل بالجدار. يمكن ضغط الزنبرك أو تمديده. يُحدد موضع الاتزان بـ x = 0.00 m، ويتم العمل على الكتلة، ويتم سحبها إلى x = + 0.02 m، وتحرر الكتلة من السكون وتتأرجح بين x = + 0.02 m و x = −0.02 m، ومدة الحركة هي 1.57 ثانية، أوجد معادلات الحركة.
إستراتيجية
نجد أولاً التردد الزاوي. التحول الطوري هو صفر،\(\phi\) = 0.00 راد، لأن الكتلة يتم تحريرها من السكون عند x = A = + 0.02 m، وبمجرد العثور على التردد الزاوي، يمكننا تحديد السرعة القصوى والحد الأقصى للعجلة.
الحل
يمكن العثور على التردد الزاوي واستخدامه للعثور على السرعة القصوى والتسارع الأقصى:
\[\begin{split} \omega & = \frac{2 \pi}{1.57\; s} = 4.00\; s^{-1}; \\ v_{max} & = A \omega = (0.02\; m)(4.00\; s^{-1}) = 0.08\; m/s; \\ a_{max} & = A \omega^{2} = (0.02; m)(4.00\; s^{-1})^{2} = 0.32\; m/s^{2} \ldotp \end{split}\]
كل ما تبقى هو ملء معادلات الحركة:
\[\begin{split} x(t) & = a \cos (\omega t + \phi) = (0.02\; m) \cos (4.00\; s^{-1} t); \\ v(t) & = -v_{max} \sin (\omega t + \phi) = (-0.8\; m/s) \sin (4.00\; s^{-1} t); \\ a(t) & = -a_{max} \cos (\omega t + \phi) = (-0.32\; m/s^{2}) \cos (4.00\; s^{-1} t) \ldotp \end{split}\]
الأهمية
يمكن العثور على الموضع والسرعة والتسارع في أي وقت. من المهم أن تتذكر أنه عند استخدام هذه المعادلات، يجب أن تكون الآلة الحاسبة في وضع الراديان.
فترة وتواتر الكتلة في الربيع
إحدى الخصائص المثيرة للاهتمام لـ SHM لجسم متصل بنابض هي أن التردد الزاوي، وبالتالي فترة الحركة وترددها، يعتمدان فقط على الكتلة وثابت القوة، وليس على عوامل أخرى مثل سعة الحركة. يمكننا استخدام معادلات الحركة وقانون نيوتن الثاني (\(\vec{F}_{net} = m \vec{a}\)) لإيجاد معادلات التردد الزاوي والتردد والنقطة.
ضع في اعتبارك الكتلة الموجودة على زنبرك على سطح خالٍ من الاحتكاك. هناك ثلاث قوى على الكتلة: الوزن والقوة العادية والقوة الناتجة عن الزنبرك. القوتان الوحيدتان اللتان تعملان بشكل عمودي على السطح هما الوزن والقوة العادية، التي لها مقادير متساوية واتجاهين متعاكسين، وبالتالي مجموعها صفر. القوة الوحيدة التي تعمل بالتوازي مع السطح هي القوة الناتجة عن الزنبرك، لذلك يجب أن تكون القوة الصافية مساوية لقوة الزنبرك:
\[\begin{split} F_{x} & = -kx; \\ ma & = -kx; \\ m \frac{d^{2} x}{dt^{2}} & = -kx; \\ \frac{d^{2} x}{dt^{2}} & = - \frac{k}{m} x \ldotp \end{split}\]
استبدال معادلات الحركة بـ x و a يعطينا
\[-A \omega^{2} \cos (\omega t + \phi) = - \frac{k}{m} A \cos (\omega t +\phi) \ldotp\]
إلغاء المصطلحات المتشابهة وحل عوائد التردد الزاوي
\[\omega = \sqrt{\frac{k}{m}} \ldotp \label{15.9}\]
يعتمد التردد الزاوي فقط على ثابت القوة والكتلة وليس السعة. يُعرَّف التردد الزاوي بأنه\(\omega = \frac{2 \pi}{T}\)، مما ينتج عنه معادلة لفترة الحركة:
\[T = 2 \pi \sqrt{\frac{m}{k}} \ldotp \label{15.10}\]
تعتمد الفترة أيضًا فقط على الكتلة وثابت القوة. كلما زادت الكتلة، كلما طالت الفترة. كلما كان الربيع أكثر صلابة، كانت الفترة أقصر. التردد هو
\[f = \frac{1}{T} = \frac{1}{2 \pi} \sqrt{\frac{k}{m}} \ldotp \label{15.11}\]
حركة عمودية ونبع أفقي
عندما يتم تعليق الزنبرك عموديًا ويتم تثبيت الكتلة وضبطها في الحركة، تتأرجح الكتلة في SHM. في هذه الحالة، لا توجد قوة طبيعية، والتأثير الصافي لقوة الجاذبية هو تغيير موضع التوازن. ضع في اعتبارك الشكل\(\PageIndex{8}\). تعمل قوتان على الكتلة: وزن وقوة الزنبرك. الوزن ثابت وتتغير قوة الزنبرك مع تغير طول الزنبرك.
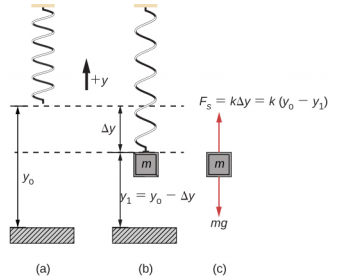
عندما تصل الكتلة إلى موضع التوازن، كما هو موضح في الشكل\(\PageIndex{8}\)، تساوي قوة الزنبرك وزن الكتلة، صافي F = F s − mg = 0، حيث
\[-k (- \Delta y) = mg \ldotp\]
من الشكل، التغيير في الموقف هو\( \Delta y = y_{0}-y_{1} \) ومنذ ذلك الحين\(-k (- \Delta y) = mg\)، لدينا
\[k (y_{0} - y_{1}) - mg = 0 \ldotp\]
إذا تم إزاحة الكتلة وتحريرها، فسوف تتأرجح حول موضع التوازن الجديد. كما هو موضح في الشكل\(\PageIndex{9}\)، إذا تم تسجيل موضع الكتلة كدالة للوقت، فإن التسجيل هو دالة دورية. إذا نُقلت الكتلة إلى الموضع y، تصبح القوة الصافية F net = k (y 0 - y) − mg. لكننا وجدنا أنه في وضع التوازن، mg = k\(\Delta\) y = ky 0 − ky 1. ينتج عن استبدال الوزن في المعادلة
\[F_{net} =ky_{0} - ky - (ky_{0} - ky_{1}) = k (y_{1} - y) \ldotp\]
تذكر أن y 1 هو مجرد موضع التوازن ويمكن ضبط أي موضع ليكون النقطة y = 0.00 m، لذلك دعونا نضبط y 1 على y = 0.00 m، ثم تصبح القوة الصافية
\[\begin{split}F_{net} & = -ky; \\ m \frac{d^{2} y}{dt^{2}} & = -ky \ldotp \end{split}\]
هذا هو بالضبط ما وجدناه سابقًا للكتلة المنزلقة أفقيًا على الزنبرك. لم تعمل القوة الثابتة للجاذبية إلا على تغيير موقع توازن الكتلة. لذلك، يجب أن يكون الحل هو نفس شكل الكتلة على زنبرك أفقي، y (t) = Acos (\(\omega\)t +\(\phi\)). تحتوي معادلات السرعة والعجلة أيضًا على نفس الشكل كما في الحالة الأفقية. لاحظ أن إدراج التحول الطوري يعني أنه يمكن بالفعل نمذجة الحركة باستخدام إما دالة جيب التمام أو دالة الجيب، لأن هاتين الوظيفتين تختلفان فقط عن طريق التحول الطوري.