13E: الجاذبية (تمارين)
- Page ID
- 199924
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
أسئلة مفاهيمية
13.1 قانون نيوتن للجذب العام
- كان يُعتقد ذات مرة أن الفعل عن بعد، كما هو الحال بالنسبة للجاذبية، غير منطقي وبالتالي غير صحيح. ما هو المحدد النهائي للحقيقة في العلم، ولماذا تم قبول هذا الإجراء عن بعد في نهاية المطاف؟
- في قانون الجاذبية العامة، افترض نيوتن أن القوة كانت متناسبة مع حاصل ضرب الكتلتين (~m 1 m 2). بينما يجب التحقق من جميع التخمينات العلمية تجريبيًا، هل يمكنك تقديم حجج حول سبب ضرورة ذلك؟ (قد ترغب في النظر في أمثلة بسيطة يؤدي فيها أي شكل آخر إلى نتائج متناقضة.)
13.2 الجاذبية بالقرب من سطح الأرض
- هل يجب على المهندسين أخذ دوران الأرض في الاعتبار عند إنشاء مبانٍ شاهقة جدًا في أي مكان آخر غير خط الاستواء أو بالقرب جدًا من القطبين؟
13.3 طاقة وضع الجاذبية والطاقة الكلية
- وقيل إن الساتل ذي الطاقة الإجمالية السالبة يقع في مدار محدد، في حين أن الساتل الذي تبلغ طاقته الإجمالية صفر أو الموجبة يقع في مدار غير محدود. لماذا هذا صحيح؟ ما هو اختيار طاقة الجاذبية الكامنة بحيث يكون هذا صحيحًا؟
- وقد تبين أن الطاقة اللازمة لرفع القمر الصناعي إلى مدار أرضي منخفض (التغيير في الطاقة الكامنة) ليست سوى جزء صغير من الطاقة الحركية اللازمة لإبقائه في المدار. هل هذا صحيح بالنسبة للمدارات الأكبر؟ هل هناك اتجاه لنسبة الطاقة الحركية للتغير في الطاقة الكامنة مع زيادة حجم المدار؟
13.4 مدارات الأقمار الصناعية والطاقة
- يجادل أحد الطلاب بأن القمر الصناعي في المدار يتعرض للسقوط الحر لأن القمر الصناعي يستمر في السقوط نحو الأرض. يقول آخر إن القمر الصناعي في المدار ليس في حالة سقوط حر لأن التسارع الناتج عن الجاذبية ليس 9.80 م/ث 2. مع من تتفق ولماذا؟
- يتم وضع العديد من الأقمار الصناعية في مدارات متزامنة مع الأرض. ما الذي يميز هذه المدارات؟ بالنسبة لشبكة اتصالات عالمية، كم من هذه الأقمار الصناعية ستكون مطلوبة؟
13.5 قوانين كيبلر لحركة الكواكب
- هل قوانين كيبلر وصفية بحتة، أم أنها تحتوي على معلومات سببية؟
- في الرسم البياني أدناه، بالنسبة للقمر الصناعي الموجود في مدار بيضاوي الشكل بكتلة أكبر بكثير، حدد أين تكون سرعته أكبر وأين تكون أقل سرعة. ما قانون الحفظ الذي يملي هذا السلوك؟ حدد اتجاهات القوة والتسارع والسرعة في هذه النقاط. ارسم متجهات لهذه الكميات الثلاث نفسها عند النقطتين حيث يتقاطع المحور yaxis (على طول المحور شبه الثانوي) ومن ثم حدد ما إذا كانت السرعة تتزايد في التناقص أم عند الحد الأقصى/الأدنى.
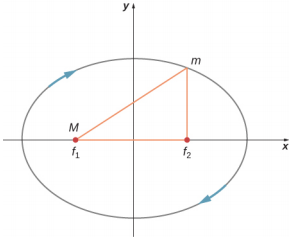
13.6 قوى المد والجزر
- عندما يسقط جسم في ثقب أسود، تزداد قوى المد والجزر. هل ستقوم قوى المد والجزر هذه دائمًا بتمزيق الجسم عند اقترابه من نصف قطر شوارزشيلد؟ كيف تؤثر كتلة الثقب الأسود وحجم الكائن على إجابتك؟
13.7 نظرية الجاذبية لأينشتاين
- ينص مبدأ التكافؤ على أن جميع التجارب التي أجريت في المختبر في مجال الجاذبية الموحد لا يمكن تمييزها عن تلك التي أجريت في مختبر ليس في مجال الجاذبية ولكنه يتسارع بشكل موحد. بالنسبة للحالة الأخيرة، ضع في اعتبارك ما يحدث لشعاع ليزر على ارتفاع معين يتم تصويره أفقيًا تمامًا على الأرض، عبر مختبر التسريع. (اعرض هذا من إطار غير متسارع خارج التمرين المعملي.) بالنسبة لارتفاع الليزر، أين سيصطدم شعاع الليزر بالجدار البعيد؟ ماذا يقول هذا عن تأثير مجال الجاذبية على الضوء؟ هل حقيقة أن الضوء ليس له كتلة تحدث فرقًا في الحجة؟
- عندما يقترب الشخص من نصف قطر شوارزشيلد للثقب الأسود، يرى المراقبون الخارجيون أن جميع عمليات ذلك الشخص (ساعاته ومعدل ضربات قلبه وما إلى ذلك) تتباطأ وتتوقف عند وصوله إلى دائرة نصف قطر شوارزشيلد. (يرى الشخص الذي يسقط في الثقب الأسود عملياته الخاصة غير متأثرة.) لكن سرعة الضوء هي نفسها في كل مكان لجميع المراقبين. ماذا يقول هذا عن الفضاء عندما تقترب من الثقب الأسود؟
مشاكل
13.1 قانون نيوتن للجذب العام
- أوجد مقدار قوة الجاذبية بين كرتين فولاذيتين كرويتين بوزن ٥ كجم تفصل بينهما مسافة من المركز إلى المركز مقدارها ١٥ سم.
- قدِّر قوة الجاذبية بين اثنين من مصارعي السومو، بكتلاتهما ٢٢٠ كجم و٢٤٠ كجم، عند احتضانهم وكان مركزاهما على مسافة ١٫٢ متر.
- يحدد علم التنجيم الكثير من موقع الكواكب في لحظة ولادة المرء. القوة الوحيدة المعروفة التي يمارسها الكوكب على الأرض هي الجاذبية. (أ) احسب قوة الجاذبية التي تؤثر على طفل وزنه 4.20 كجم بواسطة أب وزنه 100 كجم على بعد 0.200 متر عند الولادة (يقوم بالمساعدة، لذا فهو قريب من الطفل). (ب) احسب القوة المؤثِّرة على الطفل بسبب المشتري إذا كان على بُعد مسافة قريبة منه إلى الأرض، أي حوالي 6.29 x 10 11 مترًا. كيف تقارن قوة المشتري على الطفل بقوة الأب على الطفل؟ كما تمارس الأجسام الأخرى في الغرفة ومبنى المستشفى قوى جاذبية مماثلة. (بالطبع، قد تكون هناك قوة غير معروفة تعمل، لكن يحتاج العلماء أولاً إلى الاقتناع بوجود تأثير، ناهيك عن أن قوة غير معروفة تسببه.)
- يُؤثِّر جبل على بُعد 10.0 km من شخص ما قوة جاذبية عليه تساوي 2.00% من وزنه. (أ) احسب كتلة الجبل. (ب) قارن كتلة الجبل بكتلة الأرض. (ج) ما هو الشيء غير المعقول في هذه النتائج؟ (د) ما هي الأماكن غير المعقولة أو غير المتسقة؟ (لاحظ أن قياسات الجاذبية الدقيقة يمكنها بسهولة اكتشاف تأثير الجبال القريبة والاختلافات في الجيولوجيا المحلية.)
- تبلغ كتلة محطة الفضاء الدولية حوالي 370,000 كجم. (أ) ما هي القوة التي تؤثر على رائدة الفضاء المناسبة التي تزن 150 كيلوغراماً إذا كانت على بعد 20 متراً من مركز كتلة المحطة؟ (ب) ما مدى دقة إجابتك في رأيك؟

- مر الكويكب Toutatis بالقرب من الأرض في عام 2006 بأربعة أضعاف المسافة إلى قمرنا. كان هذا هو أقرب نهج سنتبعه حتى عام 2060. إذا كانت كتلتها ٥٫٠ × ١٠ ١٣ كجم، فما القوة التي مارستها على الأرض عند اقترابها الأقرب؟
- (أ) ما هو تسارع الأرض الذي أحدثه الكويكب توتاتيس (انظر المشكلة السابقة) في أقرب وقت ممكن؟ (ب) ما هو تسارع توتاتيس في هذه المرحلة؟
13.2 الجاذبية بالقرب من سطح الأرض
- (أ) احسب كتلة الأرض بمعلومية التسارع الناتج عن الجاذبية عند القطب الشمالي وقياسه ليكون 9.832 m/s 2 ونصف قطر الأرض عند القطب هو 6356 كم. (ب) قارن ذلك بقيمة صحيفة وقائع الأرض الصادرة عن وكالة ناسا والتي تبلغ 5.9726 × 10 24 كجم.
- (أ) ما هو التسارع الناتج عن الجاذبية على سطح القمر؟ (ب) على سطح المريخ؟ تبلغ كتلة المريخ 6.418 × 10 23 كجم ونصف قطره 3.38 × 10 6 م.
- (أ) احسب التسارع الناتج عن الجاذبية على سطح الشمس. (ب) بأي عامل سيزيد وزنك إذا تمكنت من الوقوف على الشمس؟ (ناهيك عن أنك لا تستطيع ذلك.)
- كتلة الجسيم تساوي ١٥ كجم. (أ) ما وزنه على الأرض؟ (ب) ما وزنه على القمر؟ (ج) ما كتلته على القمر؟ (د) ما هو وزنه في الفضاء الخارجي البعيد عن أي جسم سماوي؟ (هـ) ما كتلته في هذه المرحلة؟
- على كوكب نصف قطره ١٫٢ × ١٠ ٧ م، تبلغ التسارع الناتج عن الجاذبية ١٨ م/ث ٢. ما كتلة الكوكب؟
- يبلغ متوسط قطر كوكب زحل 1.2 × 10 8 م، ويبلغ متوسط كثافة كتلته 0.69 جم/سم 3. أوجد التسارع الناتج عن الجاذبية على سطح زحل.
- يبلغ متوسط قطر كوكب عطارد 4.88 × 10 6 م، والتسارع الناتج عن الجاذبية على سطحه هو 3.78 م/ث 2. قدِّر كتلة هذا الكوكب.
- يبلغ التسارع الناتج عن الجاذبية على سطح الكوكب ثلاثة أضعاف حجمه على سطح الأرض. من المعروف أن كثافة كتلة الكوكب تبلغ ضعف كثافة الأرض. ما نصف قطر هذا الكوكب بدلالة نصف قطر الأرض؟
- يزن جسم على سطح كوكب بنفس نصف قطر الأرض 10 مرات أكثر من وزنه على الأرض. ما كتلة هذا الكوكب من حيث كتلة الأرض؟
13.3 طاقة وضع الجاذبية والطاقة الكلية
- أوجد سرعة هروب مقذوف من سطح المريخ.
- أوجد سرعة هروب مقذوف من سطح المشتري.
- ما سرعة هروب قمر صناعي يقع في مدار القمر حول الأرض؟ افترض أن القمر ليس قريبًا.
- (أ) تقييم طاقة وضع الجاذبية بين كرتين فولاذيتين كرويتين بوزن 5.00 كجم تفصل بينهما مسافة من المركز إلى المركز قدرها 15.0 سم. (ب) على افتراض أن كلاهما في حالة راحة أولية بالنسبة لبعضهما البعض في الفضاء السحيق، استخدم حفظ الطاقة لمعرفة مدى السرعة التي سينتقلان بها عند الارتطام. يبلغ نصف قطر كل كرة 5.10 سم.
- تم الكشف عن كويكب متوسط الحجم يقع على بُعد ٥٫٠ × ١٠٧ كم من الأرض وكتلته ٢٫٠ × ١٠ ١٣ كجم وهو يتجه مباشرةً نحو الأرض بسرعة ٢٫٠ كم/ث، ما هي سرعته قبل اصطدامه بالغلاف الجوي؟ (يمكنك تجاهل حجم الكويكب.)
- (أ) ما هي طاقة حركة الكويكب في المشكلة السابقة قبل اصطدامه بالأرض مباشرة؟ ب) قارن هذه الطاقة بمخرجات أكبر قنبلة انشطارية، 2100 TJ. ما تأثير ذلك على الأرض؟
- (أ) ما هو التغيّر في طاقة حمولة وزنها 1000 كيلوغرام أُخذت من السكون على سطح الأرض ووضعت في حالة سكون على سطح القمر؟ (ب) ماذا سيكون الجواب إذا أُخذت الحمولة من سطح القمر إلى الأرض؟ هل هذا حساب معقول للطاقة اللازمة لنقل الحمولة ذهابًا وإيابًا؟
13.4 مدارات الأقمار الصناعية والطاقة
- إذا كان كوكب كتلته أكثر من 1.5 مرة من كتلة الأرض يسافر في مدار الأرض، فماذا ستكون فترته؟
- كوكبان في مدارات دائرية حول نجم لهما سرعات v و 2 فولت. (أ) ما هي نسبة نصف القطر المداري للكواكب؟ (ب) ما هي نسبة فتراتها؟
- باستخدام متوسط مسافة الأرض من الشمس والفترة المدارية للأرض، (أ) أوجد التسارع المركزي للأرض في حركتها حول الشمس. (ب) قارن هذه القيمة بقيمة التسارع المركزي عند خط الاستواء بسبب دوران الأرض.
- ما نصف القطر المداري لساتل أرضي مساحته ١٫٠٠ h؟ (ب) ما هو الشيء غير المعقول في هذه النتيجة؟
- احسب كتلة الشمس بناءً على بيانات مدار الأرض وقارن القيمة التي تم الحصول عليها بالكتلة الفعلية للشمس.
- أوجد كتلة كوكب المشتري استنادًا إلى حقيقة أن متوسط نصف قطر إيو، أقمره الأعمق، ٤٢١٧٠٠ كم وفترة ١٫٧٧ يومًا.
- تشير الملاحظات الفلكية لمجرة درب التبانة إلى أن كتلتها تبلغ حوالي 8.0 × 10 11 كتلة شمسية. يقع النجم الذي يدور حول محيط المجرة على بُعد ٦٫٠ × ١٠ ٤ سنوات ضوئية من مركزها. (أ) ماذا ينبغي أن تكون الفترة المدارية لذلك النجم؟ (ب) إذا كانت مدتها 6.0 × 10 7 سنوات بدلاً من ذلك، فما كتلة المجرة؟ تُستخدم مثل هذه الحسابات للإشارة إلى وجود مادة أخرى، مثل الثقب الأسود الضخم جدًا في مركز درب التبانة.
- (أ) من أجل منع ساتل صغير من الانجراف إلى كويكب قريب، يوضع في مدار مدته 3.02 ساعات ونصف قطره 2.0 كم. ما كتلة الكويكب؟ (ب) هل تبدو هذه الكتلة معقولة بالنسبة لحجم المدار؟
- يدور القمر والأرض حول مركز الكتلة المشترك بينهما، والذي يقع على بعد حوالي 4700 كم من مركز الأرض. (يقع هذا على بعد 1690 كم تحت السطح.) (أ) احسب التسارع الناتج عن جاذبية القمر عند تلك النقطة. (ب) احسب التسارع المركزي لمركز الأرض أثناء دورانه حول تلك النقطة مرة كل شهر قمري (حوالي 27.3 d) وقارنه بالتسارع الموجود في الجزء (أ). علق على ما إذا كانوا متساوين أم لا ولماذا يجب أن يكونوا كذلك أم لا.
- تدور الشمس حول مجرة درب التبانة مرة واحدة كل 2.60 × 10 8 سنوات، مع مدار دائري تقريبًا يبلغ متوسط دائرة نصف قطرها 3.00 × 10 4 سنوات ضوئية. (السنة الضوئية هي المسافة التي يقطعها الضوء في عام واحد.) احسب التسارع المركزي للشمس في مدارها المجري. هل تدعم نتيجتك الادعاء بأنه يمكن وضع إطار مرجعي شبه ذاتي في الشمس؟ (ب) احسب متوسط سرعة الشمس في مدارها المجري. هل تفاجئك الإجابة؟
- القمر الصناعي الأرضي المتزامن مع الأرض هو الذي له فترة مدارية تبلغ يومًا واحدًا بالضبط. هذه المدارات مفيدة للاتصالات ومراقبة الطقس لأن القمر الصناعي يظل فوق نفس النقطة على الأرض (بشرط أن يدور في المستوى الاستوائي في نفس اتجاه دوران الأرض). احسب نصف قطر هذا المدار بناءً على بيانات الأرض في الملحق D.
13.5 قوانين كيبلر لحركة الكواكب
- احسب كتلة الشمس استنادًا إلى بيانات متوسط مدار الأرض وقارن القيمة التي تم الحصول عليها بالقيمة الشائعة للشمس وهي 1.989 x 10 30 kg.
- يدور Io حول كوكب المشتري بمتوسط دائرة نصف قطرها 421700 كم وفترة 1.769 يومًا. بناءً على هذه البيانات، ما كتلة المشتري؟
- عادةً ما لا يكون نصف القطر المداري «المتوسط» المدرج للأجسام الفلكية التي تدور حول الشمس متوسطًا متكاملًا ولكن يتم حسابه بحيث يعطي الفترة الصحيحة عند تطبيقه على معادلة المدارات الدائرية. بالنظر إلى ذلك، ما متوسط نصف القطر المداري بدلالة الأوج والحضيض؟
- الحضيض لمذنب هالي هو 0.586 AU و الأوج هو 17.8 AU. إذا كانت سرعته عند نقطة الحضيض 55 كم/ثانية، فما السرعة عند نقطة الأوج (1 AU = 1.496 x 10 11 m)؟ (تلميح: يمكنك استخدام إما الحفاظ على الطاقة أو الزخم الزاوي، ولكن هذا الأخير أسهل بكثير.)
- حضيض المذنب Lagerkvist هو 2.61 AU وتبلغ مدته 7.36 عامًا. أظهر أن الأوج لهذا المذنب هو 4.95 AU.
- ما نسبة السرعة عند الحضيض إلى سرعة الأوج للمذنب لاجركفيست في المشكلة السابقة؟
- يحتوي إيروس على مدار بيضاوي حول الشمس، بمسافة حضيض تبلغ 1.13 AU ومسافة الأوج 1.78 AU. ما هي فترة مداره؟
13.6 قوى المد والجزر
- (أ) ما الفرق بين القوى المؤثِّرة على كتلة مقدارها 1.0 كجم على الجانب القريب من Io والضلع البعيد الناتجة عن المشتري؟ يبلغ متوسط نصف قطر آيو 1821 كم ويبلغ متوسط نصف قطرها المداري حول كوكب المشتري 421,700 كم. (ب) قارن هذا الاختلاف مع ذلك المحسوب للفرق الخاص بالأرض بسبب القمر المحسوب في المثال 13.14. قوى المد والجزر هي سبب النشاط البركاني لـ Io.
- إذا انهارت الشمس إلى ثقب أسود، فإن نقطة اللاعودة للمحقق ستكون على بعد حوالي 3 كم من تفرد المركز. هل سيكون المحقق قادرًا على البقاء على قيد الحياة حتى على بعد 300 كم من المركز؟ أجب عن ذلك بإيجاد الفرق في جاذبية الثقوب السوداء على كتلة وزنها ١٫٠ كجم عند رأس المحقق وعند قدميه.
- تأمل الشكل 13.23 في قوى المد والجزر. يمثل هذا الرسم البياني قوى المد والجزر للمد والجزر في الربيع. ارسم مخططًا مشابهًا للمد والجزر. (تلميح: من أجل البساطة، تخيل أن الشمس والقمر يساهمان بالتساوي. سيكون الرسم التخطيطي الخاص بك هو المجموع المتجه لحقلي القوة (كما في الشكل 13.23)، ويتم تقليله بعامل اثنين، ويتم تثبيته بزاوية قائمة.)
13.7 نظرية الجاذبية لأينشتاين
- ما نصف قطر Schwarzschild للثقب الأسود في مركز مجرتنا إذا كانت كتلته تبلغ 4 ملايين كتلة شمسية؟
- ماذا سيكون نصف قطر شوارزشيلد، في السنوات الضوئية، إذا انهارت مجرة درب التبانة المكونة من 100 مليار نجم إلى ثقب أسود؟ قارن هذا ببعدنا عن المركز، حوالي 13000 سنة ضوئية.
مشاكل إضافية
- النجم النيوتروني هو نجم بارد ومنهار بكثافة نووية. نجم نيوتروني معيّن كتلته ضعف كتلة شمسنا ونصف قطر 12.0 كم. (أ) ماذا سيكون وزن رائد فضاء وزنه 100 كجم عند وقوفه على سطحه؟ (ب) ماذا يخبرنا هذا عن الهبوط على نجم نيوتروني؟
- (أ) إلى أي مدى ستكون قوة الجاذبية الصافية للأرض والقمر على جسم ما صفرًا من مركز الأرض؟ (ب) ينبغي أن يؤدي تحديد مقادير القوى المتساوية إلى إجابتين من الدرجة التربيعية. هل تفهم سبب وجود مركزين، ولكن موقف واحد فقط تكون فيه القوة الصافية صفرًا؟
- ما مدى بُعد قوة الجاذبية الكلية للأرض والشمس على متن سفينة فضائية عن مركز الشمس؟
- احسب قيم g على سطح الأرض للتغييرات التالية في خصائص الأرض: (أ) تضاعف كتلتها ونصف قطرها إلى النصف؛ (ب) تضاعف كثافة كتلتها ونصف قطرها؛ (ج) انخفضت كثافة كتلتها إلى النصف ولم تتغير كتلتها.
- لنفترض أنه يمكنك التواصل مع سكان كوكب في نظام شمسي آخر. يخبرونك أنه على كوكبهم، الذي يبلغ قطره وكتلته 5.0 × 10 3 كم و 3.6 × 10 23 كجم، على التوالي، فإن الرقم القياسي للقفز العالي هو 2.0 متر، وبالنظر إلى أن هذا الرقم القياسي يقترب من 2.4 متر على الأرض، فما الذي ستستنتجه بشأن قدرة أصدقائك على القفز من خارج كوكب الأرض؟
- (أ) لنفترض أن وزنك المقاس عند خط الاستواء هو نصف وزنك المقاس عند القطب على كوكب تتساوى كتلته وقطره مع كتلة وقطر الأرض. ما هي فترة دوران الكوكب؟ (ب) هل تحتاج إلى أخذ شكل هذا الكوكب في الاعتبار؟
- وزن جسم كتلته ١٠٠ كجم عند القطب الشمالي وعند خط الاستواء بمقياس زنبركي. ما قراءة المقياس عند هاتين النقطتين؟ افترض أن g = 9.83 م/ث 2 عند القطب.
- أوجد السرعة اللازمة للهروب من النظام الشمسي بدءًا من سطح الأرض. افترض عدم وجود هيئات أخرى معنية ولا تأخذ في الاعتبار حقيقة أن الأرض تتحرك في مدارها. [تلميح: لا تنطبق المعادلة 13.6. استخدم المعادلة 13.5 وقم بتضمين الطاقة الكامنة لكل من الأرض والشمس.
- ضع في اعتبارك المشكلة السابقة وقم بتضمين حقيقة أن الأرض تبلغ سرعتها المدارية حول الشمس 29.8 كم/ساعة. (أ) ما هي السرعة المطلوبة بالنسبة للأرض وفي أي اتجاه يجب أن تغادر الأرض؟ (ب) ماذا سيكون شكل المسار؟
- لوحظ وجود مذنب على بُعد 1.50 AU من الشمس بسرعة 24.3 km/s. هل يوجد هذا المذنب في مدار محدد أم غير مرتبط؟
- تبلغ سرعة الكويكب 15.5 km/s عندما يقع على بُعد 2.00 AU من الشمس. عند اقترابها الأقرب، تقع على بعد 0.400 AU من الشمس. ما سرعتها عند هذه النقطة؟
- أصبح الحطام الفضائي المتبقي من الأقمار الصناعية القديمة وقاذفاتها خطرًا على الأقمار الصناعية الأخرى. (أ) احسب سرعة ساتل في مدار على ارتفاع 900 كم فوق سطح الأرض. (ب) لنفترض وجود برشام سائب في مدار بنفس نصف القطر الذي يتقاطع مع مدار الساتل بزاوية 90 درجة. ما سرعة البرشام بالنسبة إلى القمر الصناعي قبل اصطدامه مباشرة؟ (ج) إذا كانت كتلته 0.500 جم واستقر داخل الساتل، فما مقدار الطاقة التي يولدها التصادم بالجول؟ (لنفترض أن سرعة القمر الصناعي لا تتغير بشكل ملحوظ، لأن كتلته أكبر بكثير من كتلة البرشام.)
- يوجد قمر صناعي كتلته ١٠٠٠ كجم في مدار دائري حول الأرض. نصف قطر مدار القمر الصناعي يساوي ضعف نصف قطر الأرض. (أ) كم يبعد الساتل؟ (ب) أوجد طاقة الساتل الحركية والإمكانات والإجمالية.
- بعد ترقية Ceres إلى كوكب قزم، أصبحنا الآن نتعرف على أكبر كويكب معروف هو Vesta، بكتلة 2.67 × 10 20 كجم وقطر يتراوح من 578 كم إلى 458 كم. بافتراض أن Vesta كروية نصف قطرها ٥٢٠ كم، فأوجد سرعة الهروب التقريبية من سطحها.
- (أ) باستخدام البيانات الواردة في المشكلة السابقة المتعلقة بالكويكب فيستا، ما هي الفترة المدارية لمسبار فضائي في مدار دائري يبعد 10.0 كم عن سطحه؟ (ب) لماذا يعتبر هذا الحساب مفيداً بشكل هامشي في أحسن الأحوال؟
- ما السرعة المدارية لنظامنا الشمسي حول مركز درب التبانة؟ افترض أن الكتلة داخل كرة نصف قطرها تساوي المسافة التي تفصلنا عن المركز تساوي حوالي 100 مليار كتلة شمسية. المسافة التي تفصلنا عن المركز هي 27000 سنة ضوئية.
- (أ) باستخدام المعلومات الواردة في المشكلة السابقة، ما السرعة التي تحتاجها للهروب من مجرة درب التبانة من موقعنا الحالي؟ (ب) هل تحتاج إلى تسريع سفينة فضائية بهذه السرعة بالنسبة للأرض؟
- يجب أن تحتوي المدارات الدائرية في المعادلة 13.10 للأقسام المخروطية على الانحراف المركزي صفر. من هذا، وباستخدام قانون نيوتن الثاني المطبق على التسارع المركزي، أظهر أن قيمة ألفا في المعادلة 13.10 تُعطى من خلال\(\alpha = \frac{L^{2}}{GMm^{2}}\) المكان L الذي يمثل فيه الزخم الزاوي للجسم المداري. قيمة α ثابتة ويتم إعطاؤها بواسطة هذا التعبير بغض النظر عن نوع المدار.
- أظهر أنه بالنسبة إلى الانحراف المركزي الذي يساوي واحدًا في المعادلة 13.10 للأقسام المخروطية، فإن المسار هو المكافئ. قم بذلك عن طريق استبدال الإحداثيات الكارتيزية، x و y، بالإحداثيات القطبية، r و\(\theta\)، وإظهار أنها تحتوي على الشكل العام للقطع المكافئ، x = ay 2 + بواسطة + c.
- باستخدام التقنية الموضَّحة في مدارات الأقمار الصناعية والطاقة، أظهر أن كتلتين م ١ وم ٢ في مدارات دائرية حول مركز كتلتهما المشترك ستحصلان على طاقة إجمالية\(E = K + E = K_{1} + k_{2} - \frac{Gm_{1} m_{2}}{r} = - \frac{G m_{1} m_{2}}{2r}\). لقد أظهرنا الطاقة الحركية لكلتا الكتلتين بشكل صريح. (تلميح: تدور الكتل عند أنصاف أقطار r 1 و r 2، على التوالي، حيث r = r 1 + r 2. تأكد من عدم الخلط بين نصف القطر المطلوب لتسريع الجاذبية المركزية مع قوة الجاذبية.)
- بالنظر إلى مسافة الحضيض والمسافة p ومسافة الأوج، تُظهِر q، بالنسبة لمدار بيضاوي الشكل، أن السرعة عند نقطة الحضيض، v p، تُعطى بواسطة\(v_{p} = \sqrt{\frac{2GM_{Sun}}{(q + p)} \frac{q}{p}}\). (تلميح: استخدم الحفاظ على الزخم الزاوي لربط v p و v q، ثم استبدله بمعادلة حفظ الطاقة.)
- يبلغ محيط المذنب P/1999 R1 0.0570 AU ويبلغ ارتفاعه 4.99 AU. باستخدام نتائج المشكلة السابقة، ابحث عن سرعتها عند aphelion. (تلميح: التعبير هو للحضيض. استخدم التماثل لإعادة كتابة تعبير الأوج.)
مشاكل التحدي
- يتم حفر نفق في مركز كوكب كروي تمامًا وخالي من الهواء يبلغ نصف قطره R. باستخدام تعبير g المشتق في الجاذبية بالقرب من سطح الأرض للحصول على كثافة موحدة، أظهر أن جسيمًا كتلته m يسقط في النفق سينفذ حركة توافقية بسيطة. استنتج فترة تذبذب m وأظهر أن لها نفس فترة المدار على السطح.
- اتِّباعًا للتقنية المستخدمة في الجاذبية بالقرب من سطح الأرض، أوجد قيمة g كدالة لنصف القطر r من مركز كوكب ذو قشرة كروية ذي كثافة ثابتة\(\rho\) مع أنصاف القطر الداخلي والخارجي R داخل وخارج R. ابحث عن g لكل من R في < r < R out وr < R in. بافتراض بقاء الغلاف من الداخل خاليًا من الهواء، يرجى وصف السفر داخل كوكب القشرة الكروية.
- أظهر أن السرعة المساحية لمدار دائري نصف قطره أو حوالي كتلة M هي\(\frac{\Delta A}{\Delta t} = \frac{1}{2} \sqrt{GMr}\). هل يعطي تعبيرك القيمة الصحيحة لسرعة مساحة الأرض حول الشمس؟
- أظهر أن فترة المدار لكتلتين، m 1 و m 2، في مدارات دائرية نصف قطرها r 1 و r 2، على التوالي، حول مركز الكتلة المشترك بينهما، تُعطى من خلال\(T = 2 \pi \sqrt{\frac{r^{3}}{G(m_{1} + m_{2})}}\) المكان r = r = r 1 + r 2. (تلميح: تدور الكتل عند أنصاف أقطار r 1 و r 2، على التوالي حيث r = r 1 + r 2. استخدم تعبير مركز الكتلة للربط بين أنصاف الأقطار ولاحظ أن الكتلتين يجب أن تكون لهما لحظات متساوية ولكن معاكسة. ابدأ بعلاقة الفترة بمحيط وسرعة المدار لإحدى الكتل. استخدم نتيجة المشكلة السابقة باستخدام «momenta» في تعبيرات الطاقة الحركية.)
- أظهر أنه بالنسبة للتغيرات الصغيرة في الارتفاع h، بحيث h << R E، تنخفض المعادلة 13.4 إلى التعبير\(\Delta\) U = mgh.
- باستخدام الشكل 13.9، ارسم بعناية مخططًا للجسم الحر لحالة البندول البسيط المعلق عند خط العرض لامدا، مع تصنيف جميع القوى المؤثرة على الكتلة النقطية، m. قم بإعداد معادلات الحركة للتوازن، مع ضبط إحداثيات واحدة في اتجاه تسارع الجاذبية المركزية (باتجاه P في الرسم التخطيطي)، والآخر عمودي على ذلك. أظهر أن زاوية الانحراف\(\epsilon\)، المُعرَّفة بأنها الزاوية بين خيط البندول والاتجاه الشعاعي نحو مركز الأرض، تُعطى من خلال التعبير أدناه. ما زاوية الانحراف عند خط العرض 45 درجة؟ افترض أن الأرض هي كرة مثالية. \(\tan(\lambda + \epsilon) = \frac{g}{(g − \omega^{2} R_{E})} \tan \lambda\)،\(\omega\) أين السرعة الزاوية للأرض.
- (أ) بيّن أن قوة المد والجزر على جسم صغير كتلته م، وتُعرَّف بأنها الفرق في قوة الجاذبية التي ستؤثِّر على المتر على مسافة على جانبي الجسم القريب والبعيد، بسبب الجاذبية على مسافة R من M، تُعطى بواسطة F tidal =\(\frac{2GMm}{R^{3}} \Delta\) r حيث \(\Delta\)r هي المسافة بين الجانب القريب والبعيد و\(\Delta\) r << R. (ب) افترض أنك تسقط قدميك أولاً في الثقب الأسود في مركز مجرتنا. تبلغ كتلتها 4 ملايين كتلة شمسية. ماذا سيكون الفرق بين القوة عند رأسك وقدميك عند نصف قطر شوارزشيلد (أفق الحدث)؟ افترض أن كتلة كل من قدميك ورأسك 5.0 كجم تفصل بينهما مسافة 2.0 متر. هل ستبقى على قيد الحياة مرورًا بأفق الحدث؟
- ابحث عن سرعات نقل Hohmann،\(\Delta\) v EllipseEarth و\(\Delta\) v EllipseMars، اللازمة لرحلة إلى المريخ. استخدم المعادلة 13.7 لإيجاد السرعات المدارية الدائرية للأرض والمريخ. باستخدام المعادلة 13.4 والطاقة الكلية للقطع الناقص (مع المحور شبه الرئيسي أ)، المعطاة بواسطة E = −\(\frac{GmM_{s}}{2a}\)، أوجد السرعات المطلوبة في الأرض (الحضيض) وفي المريخ (الأوج) التي يجب أن تكون على الشكل البيضاوي الناقل. الفرق،\(\Delta\) v، عند كل نقطة هو زيادة السرعة أو سرعة النقل المطلوبة.


