13.8: نظرية أينشتاين للجاذبية
- Page ID
- 199940
- وصف كيفية تعامل نظرية النسبية العامة مع الجاذبية
- شرح مبدأ التكافؤ
- احسب نصف قطر شوارزشيلد لكائن
- لخص الأدلة على الثقوب السوداء
يتنبأ قانون نيوتن للجاذبية العامة بدقة بالكثير مما نراه داخل نظامنا الشمسي. في الواقع، كانت هناك حاجة إلى قوانين نيوتن فقط لإرسال كل مركبة فضائية بدقة في رحلتها. يمكن تحديد مسارات الكويكبات العابرة للأرض ومعظم الأجرام السماوية الأخرى بدقة فقط من خلال قوانين نيوتن. ومع ذلك، أظهرت العديد من الظواهر تباينًا عما تتنبأ به قوانين نيوتن، بما في ذلك مدار عطارد وتأثير الجاذبية على الضوء. في هذا القسم، ندرس طريقة مختلفة لتصور الجاذبية.
ثورة في المنظور
في عام 1905، نشر ألبرت أينشتاين نظريته في النسبية الخاصة. تمت مناقشة هذه النظرية بتفصيل كبير في النسبية لذلك نقول بضع كلمات فقط هنا. في هذه النظرية، لا يمكن لأي حركة أن تتجاوز سرعة الضوء - إنها السرعة القصوى للكون. تم التحقق من هذه الحقيقة البسيطة في تجارب لا حصر لها. ومع ذلك، فإن لها عواقب مذهلة - لم يعد المكان والزمان مطلقين. لا يتفق شخصان يتحركان بالنسبة لبعضهما البعض على طول الأشياء أو مرور الوقت. تقريبًا جميع الآليات التي تعلمتها في الفصول السابقة، على الرغم من دقتها بشكل ملحوظ حتى بالنسبة للسرعات التي تصل إلى عدة آلاف من الأميال في الثانية، تبدأ بالفشل عند الاقتراب من سرعة الضوء.
كان حد السرعة هذا على الكون أيضًا تحديًا للافتراض المتأصل في قانون نيوتن للجاذبية بأن الجاذبية هي قوة عمل على مسافة. أي أنه بدون اتصال جسدي، يتم إبلاغ أي تغيير في موضع كتلة واحدة على الفور إلى جميع الجماهير الأخرى. لا يأتي هذا الافتراض من أي مبدأ أول، لأن نظرية نيوتن ببساطة لا تتناول السؤال. (كان يعتقد نفس الشيء عن القوى الكهرومغناطيسية أيضًا. من الإنصاف القول إن معظم العلماء لم يكونوا مرتاحين تمامًا لمفهوم الحركة عن بعد.)
يظهر الافتراض الثاني أيضًا في قانون نيوتن لمعادلة الجاذبية 13.2.1. يُفترض أن تكون الكتل هي نفسها تمامًا تلك المستخدمة في قانون نيوتن الثاني،\(\vec{F}\) = m\(\vec{a}\). لقد وضعنا هذا الافتراض في العديد من مشتقاتنا في هذا الفصل. مرة أخرى، لا يوجد مبدأ أساسي مفاده أن هذا يجب أن يكون، ولكن النتائج التجريبية تتفق مع هذا الافتراض. في نظرية النسبية العامة اللاحقة لأينشتاين (1916)، تمت معالجة كل من هذه القضايا. كانت نظريته عبارة عن نظرية هندسة الزمكان وكيف تشوه الكتلة (والتسارع) ذلك الزمكان وتتفاعل معه. لم تكن نظرية قوى الجاذبية. إن رياضيات النظرية العامة تتجاوز نطاق هذا النص، ولكن يمكننا أن ننظر إلى بعض المبادئ الأساسية وعواقبها.
مبدأ التكافؤ
توصل أينشتاين إلى نظريته العامة جزئيًا من خلال التساؤل عن سبب عدم شعور الشخص الذي كان يعاني من السقوط الحر بوزنه. في الواقع، من الشائع الحديث عن رواد الفضاء الذين يدورون حول الأرض على أنهم عديمي الوزن، على الرغم من حقيقة أن جاذبية الأرض لا تزال قوية جدًا هناك. في نظرية أينشتاين العامة، لا يوجد فرق بين السقوط الحر وانعدام الوزن. وهذا ما يسمى بمبدأ التكافؤ. والنتيجة الطبيعية المدهشة بنفس القدر لذلك هي أنه لا يوجد فرق بين مجال الجاذبية الموحد والتسارع المنتظم في غياب الجاذبية. دعونا نركز على هذا البيان الأخير. على الرغم من أن مجال الجاذبية الموحد تمامًا غير ممكن، إلا أنه يمكننا تقريبه جيدًا.
داخل مختبر بحجم معقول على الأرض،\(\vec{g}\) يكون مجال الجاذبية متجانسًا بشكل أساسي. تنص النتيجة الطبيعية على أن أي تجارب فيزيائية يتم إجراؤها هناك لها نتائج مماثلة لتلك التي تتم في المختبر تتسارع\(\vec{a} = \vec{g}\) في الفضاء السحيق، بعيدًا عن جميع الكتل الأخرى. \(\PageIndex{1}\)يوضح الشكل المفهوم.
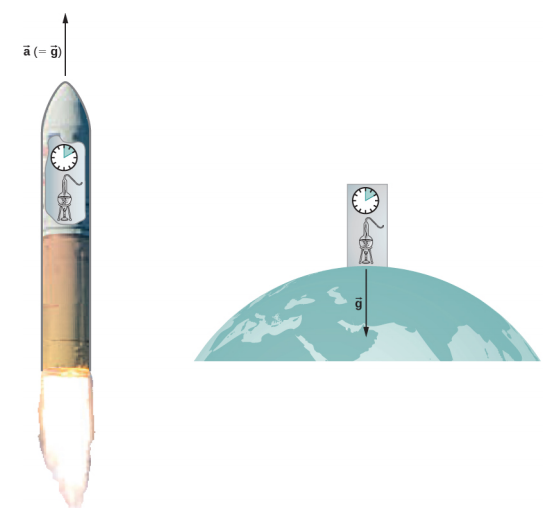
كيف يمكن أن تكون هاتان الحالتان المختلفتان جوهريًا على ما يبدو متشابهة؟ الجواب هو أن الجاذبية ليست قوة بين جسمين ولكنها نتيجة استجابة كل جسم لتأثير الآخر على الزمكان المحيط به. إن مجال الجاذبية المنتظم والتسارع المنتظم لهما نفس التأثير تمامًا على الزمكان.
نظرية هندسية للجاذبية
تفترض الهندسة الإقليدية مساحة «مسطحة» يكون فيها الخط المستقيم، من بين السمات الأكثر شيوعًا، هو أقصر مسافة بين نقطتين، ويجب أن يكون مجموع زوايا جميع المثلثات 180 درجة، ولا تتقاطع الخطوط المتوازية أبدًا. لم يتم التحقيق بجدية في الهندسة غير الإقليدية حتى القرن التاسع عشر، لذلك ليس من المستغرب أن الفضاء الإقليدي مفترض بطبيعته في جميع قوانين نيوتن.
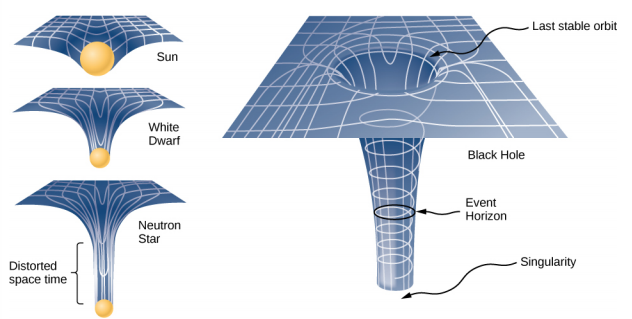
تتحدى نظرية النسبية العامة هذا الافتراض طويل الأمد. المساحة الفارغة فقط مسطحة. إن وجود الكتلة - أو الطاقة، بما أن النسبية لا تميز بين الاثنين - يشوه أو ينحني المكان والزمان، أو الزمكان، من حوله. حركة أي كتلة أخرى هي ببساطة استجابة لهذا الزمكان المنحني. الشكل\(\PageIndex{2}\) عبارة عن تمثيل ثنائي الأبعاد لكتلة أصغر تدور استجابة للفضاء المشوه الناتج عن وجود كتلة أكبر. في صورة أكثر دقة ولكن مربكة، سنرى أيضًا الفضاء مشوهًا بالكتلة المدارية، وستكون كلتا الكتلتين في حالة حركة استجابة للتشوه الكلي للفضاء. لاحظ أن الشكل عبارة عن تمثيل للمساعدة في تصور المفهوم. هذه تشوهات في الفضاء الثلاثي الأبعاد والوقت. نحن لا نراهم كما نفعل مع غمازة على الكرة. لا نرى التشويه إلا من خلال القياسات الدقيقة لحركة الأشياء والضوء أثناء تحركها عبر الفضاء.

بالنسبة لمجالات الجاذبية الضعيفة، لا تختلف نتائج النسبية العامة بشكل كبير عن قانون نيوتن للجاذبية. ولكن بالنسبة لمجالات الجاذبية الشديدة، تتباين النتائج، وقد ثبت أن النسبية العامة تتنبأ بالنتائج الصحيحة. حتى في مجال الجاذبية الضعيف نسبيًا للشمس على مسافة مدار عطارد، يمكننا ملاحظة التأثير. بدءًا من منتصف القرن التاسع عشر، تم قياس مدار عطارد الإهليلجي بعناية. ومع ذلك، على الرغم من كونه بيضاويًا، إلا أن حركته معقدة بسبب حقيقة أن موضع الحضيض للقطع الناقص يتقدم ببطء. يرجع معظم التقدم إلى قوة الجاذبية للكواكب الأخرى، لكن جزءًا صغيرًا من هذا التقدم لا يمكن تفسيره بقانون نيوتن. في وقت من الأوقات، كان هناك حتى بحث عن كوكب «رفيق» من شأنه أن يفسر التناقض. لكن النسبية العامة تتنبأ بالقياسات بشكل صحيح. منذ ذلك الحين، تحققت العديد من القياسات، مثل انحراف ضوء الأجسام البعيدة عن الشمس، من أن النسبية العامة تتنبأ بالملاحظات بشكل صحيح.
نختتم هذه المناقشة بتعليق أخير. لقد أشرنا في كثير من الأحيان إلى تشوهات الزمكان أو التشوهات في كل من المكان والزمان. في كل من النسبية الخاصة والعامة، يتساوى بُعد الوقت مع كل بُعد مكاني (يختلف في مكانه في كلتا النظريتين فقط بعامل تحجيم غير مهم في النهاية). بالقرب من كتلة كبيرة جدًا، لا يقتصر الأمر على «تمدد» المساحة القريبة، ولكن الوقت يتوسع أو «يتباطأ». نناقش هذه التأثيرات أكثر في القسم التالي.
بلاك هولز
يتم التعبير عن نظرية الجاذبية لأينشتاين في معادلة واحدة بسيطة مخادعة للموتر (الأوتار هي تعميم للأرقام القياسية والمتجهات)، والتي تعبر عن كيفية تحديد الكتلة لانحناء الزمكان المحيط بها. تسفر حلول هذه المعادلة عن واحدة من أكثر التنبؤات روعة: الثقب الأسود. التوقع هو أنه إذا كان الجسم كثيفًا بدرجة كافية، فسوف ينهار على نفسه ويكون محاطًا بأفق حدث لا يمكن لأي شيء الهروب منه. يشير اسم «الثقب الأسود»، الذي ابتكره عالم الفلك جون ويلر في عام 1969، إلى حقيقة أن الضوء لا يمكنه الهروب من مثل هذا الكائن. كان كارل شوارزشيلد أول شخص لاحظ هذه الظاهرة في عام 1916، ولكن في ذلك الوقت، كان يُنظر إليها في الغالب على أنها فضول رياضي.
والمثير للدهشة أن فكرة الجسم الضخم الذي لا يستطيع الضوء الهروب منه تعود إلى أواخر القرن الثامن عشر. وبشكل مستقل، استخدم جون ميشيل وبيير سيمون لابلاس قانون نيوتن للجاذبية لإظهار أن الضوء الذي يترك سطح نجم بكتلة كافية لا يمكنه الهروب. استند عملهم إلى حقيقة أن سرعة الضوء قد تم قياسها بواسطة Ole Roemer في عام 1676. وأشار إلى وجود اختلافات في بيانات الفترة المدارية للقمر Io حول كوكب المشتري. أدرك رويمر أن الفرق نشأ من المواقع النسبية للأرض والمشتري في أوقات مختلفة وأنه يمكن أن يجد سرعة الضوء من هذا الاختلاف. أدرك كل من Michell و Laplace أنه نظرًا لأن الضوء له سرعة محدودة، فقد يكون هناك نجم ضخم بما يكفي بحيث يمكن لسرعة الهروب من سطحه أن تتجاوز تلك السرعة. وبالتالي، سيعود الضوء دائمًا إلى النجم. ومن الغريب أن المراقبين البعيدين بما يكفي عن أكبر النجوم لن يتمكنوا من رؤيتها، ومع ذلك يمكنهم رؤية نجمة أصغر من نفس المسافة.
تذكر أنه في الطاقة الكامنة للجاذبية والطاقة الإجمالية، وجدنا أن سرعة الهروب، المعطاة بـ\(v_{\mathrm{esc}}=\sqrt{\frac{2 G M}{R}}\)، مستقلة عن كتلة الجسم المتسرب. على الرغم من أن طبيعة الضوء لم تكن مفهومة تمامًا في ذلك الوقت، إلا أن كتلة الضوء، إن وجدت، لم تكن ذات صلة. وبالتالي، يجب أن تكون هذه المعادلة صالحة للضوء. باستبدال c، سرعة الضوء، لسرعة الهروب، لدينا
\[v_{esc} = c = \sqrt{\dfrac{2GM}{R}} \ldotp\]
وبالتالي، نحتاج فقط إلى قيم R و M بحيث تتجاوز سرعة الهروب c، ومن ثم لن يتمكن الضوء من الهروب. افترض ميشيل أنه إذا كان للنجم كثافة شمسنا ونصف قطر يمتد إلى ما وراء مدار المريخ، فلن يتمكن الضوء من الهروب من سطحه. لقد توقع أيضًا أننا سنظل قادرين على اكتشاف مثل هذا النجم من تأثير الجاذبية الذي سيكون له على الأشياء المحيطة به. كان هذا استنتاجًا ثاقبًا، لأن هذه هي بالضبط الطريقة التي نستنتج بها وجود مثل هذه الأشياء اليوم. في حين أننا لم نزور الثقب الأسود بعد، وقد لا نزور أبدًا، إلا أن الأدلة الظرفية الخاصة به أصبحت مقنعة جدًا لدرجة أن قلة من علماء الفلك يشككون في وجودها.
قبل أن نفحص بعض هذه الأدلة، نعيد انتباهنا إلى حل شوارزشيلد لمعادلة الموتر من النسبية العامة. في هذا الحل ينشأ نصف قطر حرج، يسمى الآن نصف قطر شوارزشيلد (R S). بالنسبة لأي كتلة M، إذا تم ضغط هذه الكتلة إلى الحد الذي يصبح فيه نصف قطرها أقل من نصف قطر شوارزشيلد، فسوف تنهار الكتلة إلى درجة التفرد، وأي شيء يمر داخل هذا القطر لا يمكنه الهروب. بمجرد دخول R S، يأخذ سهم الوقت كل الأشياء إلى التفرد. (بالمعنى الرياضي الواسع، التفرد هو المكان الذي تذهب فيه قيمة الدالة إلى ما لا نهاية. في هذه الحالة، تكون نقطة في الفضاء بحجم صفر بكتلة محدودة. وبالتالي، تصبح كثافة الكتلة وطاقة الجاذبية غير محدودة.) يتم تحديد نصف قطر شوارزشيلد بواسطة
\[R_{S} = \dfrac{2GM}{c^{2}} \ldotp \label{13.12}\]
إذا نظرت إلى معادلة سرعة الهروب الخاصة بنا باستخدام v esc = c، ستلاحظ أنها تعطي هذه النتيجة بدقة. لكن هذا مجرد حادث عرضي ناجم عن عدة افتراضات غير صحيحة. أحد هذه الافتراضات هو استخدام التعبير الكلاسيكي غير الصحيح للطاقة الحركية للضوء. ما مدى كثافة الجسم لكي يتحول إلى ثقب أسود؟
احسب نصف قطر شوارزشيلد لكل من الشمس والأرض. قارن كثافة نواة الذرة بالكثافة المطلوبة لضغط كتلة الأرض بشكل موحد إلى نصف قطر شوارزشيلد. تبلغ كثافة النواة حوالي 2.3 × 10 17 كجم/م 3.
إستراتيجية
نحن نستخدم المعادلة\ ref {13.12} لهذا الحساب. نحتاج فقط إلى كتل الأرض والشمس، والتي نحصل عليها من البيانات الفلكية الواردة في الملحق D.
الحل
باستبدال كتلة الشمس، لدينا
\[R_{S} = \dfrac{2GM}{c^{2}} = \dfrac{2(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(1.99 \times 10^{30}\; kg)}{(3.0 \times 10^{8}\; m/s)^{2}} = 2.95 \times 10^{3}\; m \ldotp\]
يبلغ قطرها حوالي 6 كم فقط. إذا استخدمنا كتلة الأرض، نحصل على R S = 8.85 × 10 −3 م، وهو قطر أقل من 2 سم! إذا قمنا بتجميع كتلة الأرض في كرة نصف قطرها R S = 8.85 × 10 −3 m، نحصل على كثافة
\[\rho = \dfrac{mass}{volume} = \dfrac{5.97 \times 10^{24}\; kg}{\dfrac{4}{3} \pi (8.85 \times 10^{-3}\; m)^{3}} = 2.06 \times 10^{30}\; kg/m^{3} \ldotp\]
الدلالة
النجم النيوتروني هو أصغر جسم معروف - خارج الثقب الأسود نفسه. يتكون النجم النيوتروني من نيوترونات بكثافة نواة ذرية، ويُعتقد، مثل العديد من الثقوب السوداء، أنه بقايا سوبرنوفا - نجم ينفجر في نهاية عمره. لإنشاء ثقب أسود من الأرض، سيتعين علينا ضغطه إلى كثافة أكبر بثلاثة عشر درجة من حجم النجم النيوتروني. ستتطلب هذه العملية قوة لا يمكن تصورها. لا توجد آلية معروفة يمكن أن تتسبب في تحول جسم بحجم الأرض إلى ثقب أسود. بالنسبة للشمس، يجب أن تكون قادرًا على إظهار أنه سيتعين ضغطها إلى كثافة تبلغ حوالي 80 مرة فقط من كثافة النواة. (ملاحظة: بمجرد ضغط الكتلة داخل نصف قطر شوارزشيلد، تملي النسبية العامة أنها ستنهار إلى درجة التفرد. تُظهر هذه الحسابات فقط الكثافة التي يجب أن نحققها لبدء هذا الانهيار.)
ضع في اعتبارك الكثافة المطلوبة لجعل الأرض ثقبًا أسودًا مقارنة بالكثافة المطلوبة للشمس. ما هي النتيجة التي يمكنك استخلاصها من هذه المقارنة حول ما هو مطلوب لإنشاء ثقب أسود؟ هل تتوقع أن يحتوي الكون على العديد من الثقوب السوداء ذات الكتلة الصغيرة؟
أفق الحدث
يُطلق على نصف قطر Schwarzschild أيضًا اسم أفق حدث الثقب الأسود. لاحظنا أن المكان والزمان يتمددان بالقرب من الأجسام الضخمة، مثل الثقوب السوداء. \(\PageIndex{3}\)يوضح الشكل هذا التأثير على الفضاء. التشوه الذي تسببه شمسنا صغير جدًا في الواقع، والرسم التخطيطي مبالغ فيه من أجل الوضوح. تأمل النجم النيوتروني الموصوف في المثال\(\PageIndex{1}\). على الرغم من أن تشوه الزمكان على سطح النجم النيوتروني مرتفع جدًا، إلا أن نصف القطر لا يزال أكبر من نصف قطر شوارزشيلد. لا يزال بإمكان الأجسام الهروب من سطحها.
ومع ذلك، إذا اكتسب نجم نيوتروني كتلة إضافية، فسوف ينهار في النهاية، ويتقلص إلى ما وراء نصف قطر شوارزشيلد. بمجرد حدوث ذلك، سيتم سحب الكتلة بأكملها، حتمًا، إلى التفرد. في الرسم التخطيطي، تمتد المساحة إلى ما لا نهاية. يمتد الوقت أيضًا إلى ما لا نهاية. عندما تسقط الأجسام نحو أفق الحدث، نراها تقترب ببطء أكثر من أي وقت مضى، ولكنها لا تصل أبدًا إلى أفق الحدث. كمراقبين خارجيين، لا نرى أبدًا الأشياء تمر عبر أفق الحدث - على نحو فعال، يمتد الوقت إلى نقطة توقف.
قم بزيارة هذا الموقع لعرض مثال متحرك لهذه التشوهات المكانية.
الأدلة على الثقوب السوداء
لم يتجدد الاهتمام بوجود الثقوب السوداء حتى الستينيات، عندما تم اكتشاف أول نجم نيوتروني. تستند الأدلة الخاصة بالثقوب السوداء إلى عدة أنواع من الملاحظات، مثل التحليل الإشعاعي لثنائيات الأشعة السينية، وعدسة الجاذبية للضوء من المجرات البعيدة، وحركة الأجسام المرئية حول الشركاء غير المرئيين. سنركز على هذه الملاحظات اللاحقة من حيث صلتها بما تعلمناه في هذا الفصل. على الرغم من أن الضوء لا يستطيع الهروب من الثقب الأسود حتى نراه، إلا أنه يمكننا رؤية تأثير الجاذبية للثقب الأسود على الكتل المحيطة.
أقرب دليل، وربما الأكثر إثارة، على وجود ثقب أسود هو مركز مجرة درب التبانة. حددت مجموعة UCLA Galactic Group، باستخدام البيانات التي تم الحصول عليها بواسطة تلسكوبات W M. Keck، مدارات العديد من النجوم بالقرب من مركز مجرتنا. تظهر بعض هذه البيانات في الشكل\(\PageIndex{4}\). تم تسليط الضوء على مدارات نجمين. من قياسات فترات وأحجام مداراتها، تشير التقديرات إلى أنها تدور حول كتلة تبلغ حوالي 4 ملايين كتلة شمسية. لاحظ أن الكتلة يجب أن تكون موجودة في المنطقة التي تم إنشاؤها بواسطة تقاطع الأشكال البيضاوية للنجوم. ستتناسب المنطقة التي يجب أن تتواجد فيها هذه الكتلة داخل مدار الزئبق - ومع ذلك لا يوجد شيء هناك في الطيف المرئي.
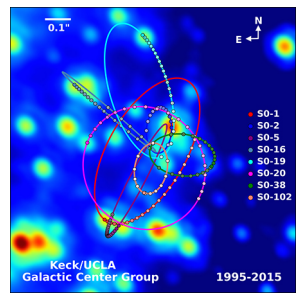
إن فيزياء إنشاء النجوم وتطورها راسخة. المصدر النهائي للطاقة التي تجعل النجوم تتألق هو طاقة الجاذبية الذاتية التي تحفز الاندماج. السلوك العام هو أنه كلما زاد حجم النجم، زاد سطوعه وكلما كان عمره أقصر. والاستدلال المنطقي هو أن الكتلة التي تبلغ 4 ملايين مرة كتلة شمسنا، والتي تقتصر على منطقة صغيرة جدًا، والتي لا يمكن رؤيتها، ليس لها تفسير قابل للتطبيق سوى الثقب الأسود. تشير الملاحظات خارج المجرة بقوة إلى أن الثقوب السوداء شائعة في مركز المجرات.
قم بزيارة الصفحة الرئيسية لمجموعة UCLA Galactic Center Group للحصول على معلومات حول ثنائيات الأشعة السينية وعدسات الجاذبية. قم بزيارة هذه الصفحة لمشاهدة تصور ثلاثي الأبعاد للنجوم التي تدور بالقرب من مركز مجرتنا، حيث توجد الرسوم المتحركة بالقرب من أسفل الصفحة.
المادة المظلمة
تقدم النجوم التي تدور بالقرب من قلب مجرتنا دليلًا قويًا على وجود ثقب أسود هناك، لكن مدارات النجوم البعيدة عن المركز تشير إلى ظاهرة أخرى مثيرة للاهتمام يتم ملاحظتها بشكل غير مباشر أيضًا. تذكر من موقع الجاذبية بالقرب من سطح الأرض أنه يمكننا النظر في كتلة الأجسام الكروية التي يجب وضعها عند نقطة في المركز لحساب تأثيرات الجاذبية على الكتل الأخرى. وبالمثل، يمكننا التعامل مع الكتلة الكلية التي تقع داخل مدار أي نجم في مجرتنا على أنها تقع في مركز قرص درب التبانة. يمكننا تقدير هذه الكتلة من خلال حساب النجوم المرئية وإدراج كتلة الثقب الأسود في المركز أيضًا في تقديرنا.
ولكن عندما نفعل ذلك، نجد أن السرعة المدارية للنجوم سريعة جدًا بحيث لا يمكن أن تنتج عن هذه الكمية من المادة. \(\PageIndex{5}\)يوضِّح الشكل السرعات المدارية للنجوم كدالة على المسافة التي تفصلها عن مركز درب التبانة. يمثل الخط الأزرق السرعات التي نتوقعها من تقديراتنا للكتلة، في حين أن المنحنى الأخضر هو ما نحصل عليه من القياسات المباشرة. يبدو أن هناك الكثير من المواد التي لا نراها، والتي تقدر بحوالي خمسة أضعاف ما نراه، لذلك تم تسميتها بالمادة المظلمة. علاوة على ذلك، لا يتبع ملف تعريف السرعة ما نتوقعه من التوزيع الملحوظ للنجوم المرئية. لا يقتصر الأمر على عدم توافق تقدير الكتلة الكلية مع البيانات فحسب، بل إن التوزيع المتوقع غير متسق أيضًا. وهذه الظاهرة لا تقتصر على مجرتنا، ولكن يبدو أنها سمة من سمات جميع المجرات. في الواقع، تمت ملاحظة المشكلة لأول مرة في ثلاثينيات القرن الماضي عندما تم قياس المجرات داخل المجموعات بحيث تدور حول مركز كتلة تلك المجموعات بشكل أسرع مما ينبغي بناءً على تقديرات الكتلة المرئية.
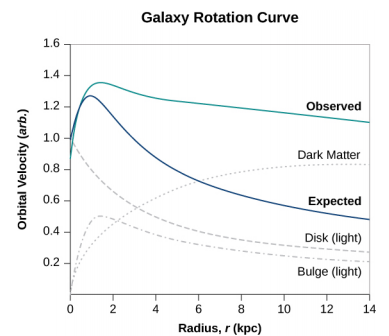
هناك فكرتان سائدتان حول ما يمكن أن يكون عليه هذا الأمر - Wimps و MacHos. يرمز WIMPs إلى الجسيمات الضخمة ذات التفاعل الضعيف. تتفاعل هذه الجسيمات (النيوترينوات هي أحد الأمثلة) بشكل ضعيف جدًا مع المادة العادية، وبالتالي يصعب اكتشافها بشكل مباشر. يرمز mACHOS إلى أجسام الهالة الضخمة المدمجة، والتي تتكون من مادة باريونية عادية، مثل النيوترونات والبروتونات. هناك مشكلات لم يتم حلها مع كل من هذه الأفكار، وستكون هناك حاجة إلى مزيد من البحث لحل اللغز.


