13.6: قوانين كيبلر لحركة الكواكب

أهداف التعلم

• وصف المقاطع المخروطية وكيفية ارتباطها بالحركة المدارية
• وصف كيفية ارتباط السرعة المدارية بالحفاظ على الزخم الزاوي
• أوجد فترة مدار بيضاوي الشكل من محوره الرئيسي

باستخدام البيانات الدقيقة التي جمعها تايكو براهي، حلل يوهانس كيبلر بعناية مواقع جميع الكواكب المعروفة والقمر في السماء، ورسم مواقعها على فترات زمنية منتظمة. من خلال هذا التحليل، قام بصياغة ثلاثة قوانين نتناولها في هذا القسم.

قانون كبلر الأول

كان الرأي السائد خلال زمن كيبلر هو أن جميع مدارات الكواكب كانت دائرية. قدمت بيانات المريخ التحدي الأكبر لوجهة النظر هذه والتي شجعت كيبلر في النهاية على التخلي عن الفكرة الشائعة. ينص قانون كيبلر الأول على أن كل كوكب يتحرك على طول الشكل البيضاوي، حيث تقع الشمس في بؤرة الشكل البيضاوي. يُعرَّف الشكل البيضاوي بأنه مجموعة كل النقاط بحيث يكون مجموع المسافة من كل نقطة إلى بؤرين ثابتًا. \(\PageIndex{1}\)يعرض الشكل الشكل الشكل البيضاوي ويصف طريقة بسيطة لإنشائه.

الشكل\(\PageIndex{1}\): (أ) الشكل البيضاوي هو منحنى يكون فيه مجموع المسافات من نقطة على المنحنى إلى بؤرين (f ₁ و f ₂) ثابتًا. من هذا التعريف، يمكنك أن ترى أنه يمكن إنشاء شكل بيضاوي بالطريقة التالية. ضع دبوسًا عند كل تركيز، ثم ضع حلقة من الخيط حول قلم رصاص والدبابيس. مع الحفاظ على تعليم الخيط، حرّك القلم الرصاص في دائرة كاملة. إذا احتلت البؤرتان نفس المكان، تكون النتيجة دائرة - حالة خاصة من الشكل البيضاوي. (ب) بالنسبة للمدار الإهليلجي، إذا كان m << M، فإن m يتبع مسارًا بيضاويًا يكون فيه M عند نقطة تركيز واحدة. بتعبير أدق، يتحرك كل من m و M في شكل بيضاوي خاص بهما حول مركز الكتلة المشترك.

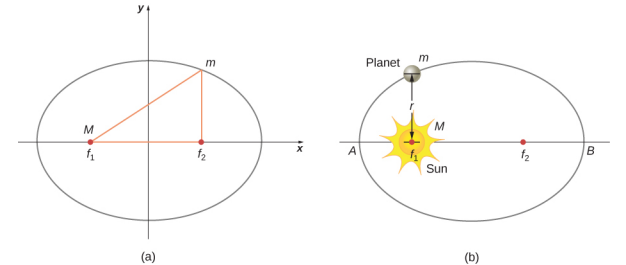
بالنسبة للمدارات الإهليلجية، فإن نقطة الاقتراب الأقرب للكوكب من الشمس تسمى الحضيض. يتم تسميتها بالنقطة A في الشكل\(\PageIndex{1}\). وأبعد نقطة هي نقطة الأوج وتسمى النقطة B في الشكل. بالنسبة لمدار القمر حول الأرض، تسمى هذه النقاط نقطة الحضيض والأوج، على التوالي.

يحتوي القطع الناقص على عدة أشكال رياضية، ولكن جميعها حالة خاصة للمعادلة الأكثر عمومية للأقسام المخروطية. هناك أربعة أقسام مخروطية مختلفة، وكلها معطاة بالمعادلة

\[\frac{\alpha}{r} = 1 + e \cos \theta \ldotp \label{13.10}\]

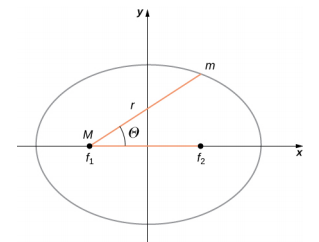
تظهر\(\theta\) المتغيرات\(r\) A في الشكل\(\PageIndex{2}\) في حالة القطع الناقص. يتم تحديد الثوابت α و e من خلال الطاقة الكلية والزخم الزاوي للقمر الصناعي عند نقطة معينة. يسمى الثابت e بالانحراف. تحدد قيم\(\alpha\) القسم e أي من المقاطع المخروطية الأربعة يمثل مسار القمر الصناعي.

الشكل\(\PageIndex{2}\): كما هو الحال من قبل، كانت المسافة بين الكوكب والشمس\(r\)، والزاوية المقاسة من المحور السيني، الذي يقع على طول المحور الرئيسي للقطع الناقص، هي\(\theta\).

إن أحد الانتصارات الحقيقية لقانون نيوتن للجاذبية الكونية، حيث تتناسب القوة مع معكوس المسافة المربعة، هو أنه عندما يتم دمجه مع قانونه الثاني، يكون الحل لمسار أي قمر صناعي هو المقطع المخروطي. كل مسار يسلكه m هو أحد الأقسام المخروطية الأربعة: دائرة أو شكل بيضاوي للمدارات المقيدة أو المغلقة، أو المكافئ أو الضخامي للمدارات غير المحدودة أو المفتوحة. تظهر هذه المقاطع المخروطية في الشكل\(\PageIndex{3}\).

الشكل\(\PageIndex{3}\): كل الحركة الناتجة عن قوة مربعة معكوسة هي واحدة من الأقسام المخروطية الأربعة ويتم تحديدها بواسطة طاقة واتجاه الجسم المتحرك

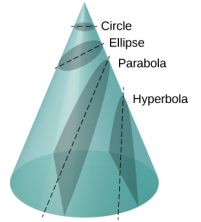
إذا كانت الطاقة الكلية سالبة، فإن 0 ≤ e < 1، وتمثل المعادلة\ ref {13.10} مدارًا مقيدًا أو مغلقًا لشكل بيضاوي أو دائرة، حيث e = 0. [يمكنك أن ترى من المعادلة 13.10 أنه بالنسبة لـ e = 0، r =\(\alpha\)، وبالتالي فإن نصف القطر ثابت.] بالنسبة للأشكال البيضاوية، يرتبط الانحراف بكيفية ظهور الشكل البيضاوي المستطيل. لا تحتوي الدائرة على أي انحراف مركزي، في حين أن الشكل البيضاوي الطويل جدًا والممتد له انحراف مركزي بالقرب من الدائرة.

إذا كانت الطاقة الإجمالية صفرًا تمامًا، فإن e = 1 والمسار هو المكافئ. تذكر أن القمر الصناعي ذو الطاقة الإجمالية الصفرية له سرعة الهروب بالضبط. (يتم تشكيل القطع المكافئ فقط عن طريق تقطيع المخروط الموازي لخط المماس على طول السطح.) أخيرًا، إذا كانت الطاقة الإجمالية موجبة، فإن e > 1 والمسار هو hyperbola. يمثل هذان المساران الأخيران مدارات غير محدودة، حيث يمر m بـ M مرة واحدة ومرة واحدة فقط. وقد لوحظ هذا الوضع للعديد من المذنبات التي تقترب من الشمس ثم تسافر بعيدًا، ولا تعود أبدًا.

لقد حصرنا أنفسنا في الحالة التي تدور فيها الكتلة الأصغر (الكوكب) حول كتلة أكبر بكثير، وبالتالي ثابتة، (الشمس)، لكن المعادلة 13.10 تنطبق أيضًا على أي كتلتين متفاعلتين بالجاذبية. كل كتلة تتتبع نفس القسم المخروطي بالضبط مثل الأخرى. يتم تحديد هذا الشكل من خلال الطاقة الكلية والزخم الزاوي للنظام، مع وجود مركز كتلة النظام عند التركيز. نسبة أبعاد المسارين هي عكس نسبة كتلتهما.

محاكاة

يمكنك مشاهدة رسم متحرك لكائنين متفاعلين في صفحة My Solar System في PhET. اختر خيار الإعداد المسبق للشمس والكوكب. يمكنك أيضًا عرض مشاكل الجسم المتعددة الأكثر تعقيدًا. قد تجد المسار الفعلي للقمر مفاجئًا للغاية، ومع ذلك يخضع لقوانين نيوتن البسيطة للحركة.

عمليات النقل المدارية

تخيل الناس السفر إلى الكواكب الأخرى في مجموعتنا الشمسية منذ اكتشافها. ولكن كيف يمكننا القيام بذلك بشكل أفضل؟ تم اكتشاف الطريقة الأكثر كفاءة في عام 1925 من قبل Walter Hohmann، المستوحاة من رواية الخيال العلمي الشهيرة في ذلك الوقت. تسمى الطريقة الآن تحويل Hohmann. في حالة الانتقال بين مدارين دائريين، يتم النقل على طول شكل بيضاوي «نقل» يعترض تمامًا تلك المدارات عند الأوج وحضيض الشكل البيضاوي. \(\PageIndex{4}\)يوضح الشكل حالة الرحلة من مدار الأرض إلى مدار المريخ. كما كان الحال من قبل، كانت الشمس في بؤرة القطع الناقص.

بالنسبة لأي شكل بيضاوي، يتم تعريف المحور شبه الرئيسي على أنه نصف مجموع الحضيض ونقطة الأوج. في الشكل\(\PageIndex{4}\)، يمثل المحور شبه الرئيسي المسافة من نقطة الأصل إلى أي من جانبي الشكل البيضاوي على طول المحور السيني، أو نصف أطول محور فقط (يسمى المحور الرئيسي). وبالتالي، للانتقال من مدار دائري نصف قطره r ₁ إلى مدار دائري آخر نصف قطره r ₂، سيكون أوج الشكل البيضاوي الانتقالي مساويًا لقيمة المدار الأكبر، بينما سيكون الحضيض هو المدار الأصغر. لذلك يتم إعطاء المحور شبه الرئيسي، الذي يُشار إليه بـ a، بواسطة\(a = \frac{1}{2} (r_{1} + r_{2})\).

الشكل\(\PageIndex{4}\): يحتوي القطع الناقص على نقطة الحضيض الانتقالي في مدار الأرض ونقطة الأوج في مدار المريخ.

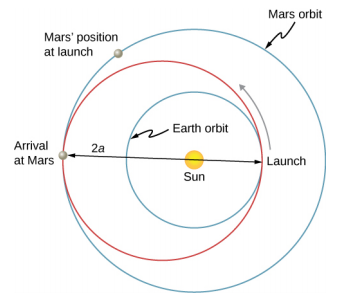
لنأخذ حالة السفر من الأرض إلى المريخ. في الوقت الحالي، نتجاهل الكواكب ونفترض أننا وحدنا في مدار الأرض ونرغب في الانتقال إلى مدار المريخ. من المعادلة 13.9، التعبير عن الطاقة الكلية، يمكننا أن نرى أن الطاقة الإجمالية لمركبة فضائية في المدار الأكبر (المريخ) أكبر (أقل سالبة) من تلك الخاصة بالمدار الأصغر (الأرض). للانتقال إلى الشكل البيضاوي الانتقالي من مدار الأرض، سنحتاج إلى زيادة طاقتنا الحركية، أي أننا بحاجة إلى زيادة السرعة. الطريقة الأكثر كفاءة هي التسارع السريع جدًا على طول المسار المداري الدائري، والذي يقع أيضًا على طول مسار القطع الناقص عند تلك النقطة. (في الواقع، يجب أن يكون التسارع فوريًا، بحيث تتطابق المدارات الدائرية والإهليلجية أثناء التسارع. من الناحية العملية، يكون التسارع المحدود قصيرًا بما يكفي بحيث لا يمثل الفرق اعتبارًا مهمًا.) بمجرد وصولك إلى مدار المريخ، ستحتاج إلى دفعة أخرى للسرعة للانتقال إلى هذا المدار، أو ستبقى في المدار الإهليلجي وستعود ببساطة إلى نقطة الحضيض حيث بدأت. بالنسبة لرحلة العودة، يمكنك ببساطة عكس العملية من خلال تعزيز رجعي في كل نقطة تحويل.

للانتقال إلى الشكل البيضاوي الانتقالي ثم إيقافه مرة أخرى، نحتاج إلى معرفة سرعة كل مدار دائري وسرعات مدار النقل عند الحضيض والدوران. زيادة السرعة المطلوبة هي ببساطة الفرق بين سرعة المدار الدائري وسرعة المدار الإهليلجي عند كل نقطة. يمكننا إيجاد السرعات المدارية الدائرية من المعادلة 13.7. لتحديد سرعات الشكل البيضاوي، نذكر بدون دليل (لأنه خارج نطاق هذه الدورة) أن الطاقة الإجمالية للمدار الإهليلجي هي

\[E = - \frac{GmM_{S}}{2a}\]

حيث M _S هي كتلة الشمس و a هو المحور شبه الرئيسي. ومن اللافت للنظر أن هذه هي نفس المعادلة 13.9 للمدارات الدائرية، ولكن بقيمة المحور شبه الرئيسي لتحل محل نصف القطر المداري. نظرًا لأننا نعرف طاقة الجهد من المعادلة 13.4، يمكننا إيجاد طاقة الحركة وبالتالي السرعة اللازمة لكل نقطة على الشكل البيضاوي. نترك الأمر كمشكلة صعبة للعثور على سرعات النقل هذه لرحلة من الأرض إلى المريخ.

ننهي هذه المناقشة بالإشارة إلى بعض التفاصيل المهمة. أولاً، لم نحسب الطاقة الكامنة في الجاذبية بسبب الأرض والمريخ، أو آليات الهبوط على المريخ. في الممارسة العملية، يجب أن يكون ذلك جزءًا من الحسابات. ثانيًا، التوقيت هو كل شيء. لا تريد الوصول إلى مدار المريخ لتكتشف أنه غير موجود. يجب أن نترك الأرض في الوقت الصحيح تمامًا بحيث يكون المريخ في قمة القطع الناقص الخاص بنا بمجرد وصولنا. تأتي هذه الفرصة كل عامين تقريبًا. وتتطلب العودة توقيتًا صحيحًا أيضًا. ستستغرق الرحلة الإجمالية أقل من 3 سنوات! هناك خيارات أخرى توفر عبورًا أسرع، بما في ذلك الطيران بمساعدة الجاذبية فوق كوكب الزهرة. لكن هذه الخيارات الأخرى تأتي بتكلفة إضافية في الطاقة وخطر على رواد الفضاء.

ملاحظة

قم بزيارة هذا الموقع (https://openstaxcollege.org/l/21plantripmars) لمزيد من التفاصيل حول التخطيط لرحلة إلى المريخ.

قانون كبلر الثاني

ينص قانون كبلر الثاني على أن الكوكب يجتاح مساحات متساوية في أوقات متساوية، أي أن المنطقة المقسمة على الزمن، والتي تسمى السرعة المساحية، ثابتة. ضع في اعتبارك الشكل\(\PageIndex{5}\). الوقت الذي يستغرقه الكوكب للانتقال من الموقع A إلى B، واجتياح المنطقة A ₁، هو بالضبط الوقت المستغرق للانتقال من الموضع C إلى D، وكنس المنطقة A ₂، والانتقال من E إلى F، واجتياح المنطقة A ₃. هذه المناطق هي نفسها: A ₁ = A ₂ = A ₃.

الشكل\(\PageIndex{5}\): تحتوي المناطق المظللة الموضحة على مساحات متساوية وتمثل نفس الفترة الزمنية.

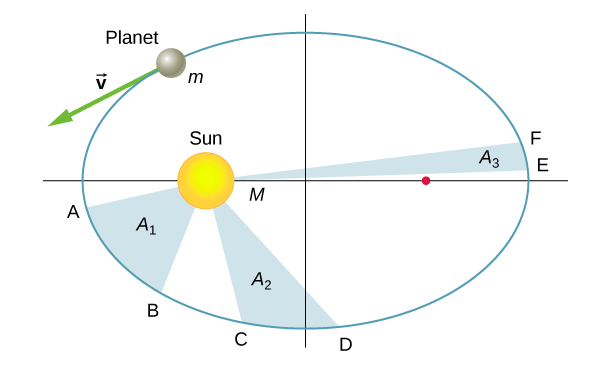
بمقارنة المساحات في الشكل والمسافة المقطوعة على طول الشكل البيضاوي في كل حالة، يمكننا أن نرى أنه لكي تكون المناطق متساوية، يجب أن يتسارع الكوكب عندما يقترب من الشمس ويبطئ أثناء ابتعاده. يتوافق هذا السلوك تمامًا مع معادلة الحفظ الخاصة بنا، المعادلة\ ref {13.5}. لكننا سنبين أن قانون كيبلر الثاني هو في الواقع نتيجة للحفاظ على الزخم الزاوي، والذي ينطبق على أي نظام له قوى شعاعية فقط.

تذكر تعريف الزخم الزاوي من الزخم الزاوي،\(\vec{L} = \vec{r} \times \vec{p}\). في حالة الحركة المدارية،\(\vec{L}\) يكون الزخم الزاوي للكوكب حول الشمس،\(\vec{r}\) هو متجه موقع الكوكب المقاس من الشمس، و\(\vec{p}\) = m\(\vec{v}\) هو الزخم الخطي اللحظي في أي نقطة في المدار. نظرًا لأن الكوكب يتحرك على طول الشكل البيضاوي، فإنه دائمًا\(\vec{p}\) ما يكون مماسًا للقطع الناقص.

يمكننا حل الزخم الخطي إلى مكونين: مكون شعاعي\(\vec{p}_{rad}\) على طول خط الشمس، ومكون\(\vec{p}_{perp}\) عمودي على\(\vec{r}\). يمكن بعد ذلك كتابة المنتج المتقاطع للزخم الزاوي كـ

\[\begin{align*} \vec{L} &= \vec{r} \times \vec{p} \\[4pt] &= \vec{r} \times (\vec{p}_{rad} + \vec{p}_{perp}) \\[4pt] &= \vec{r} \times \vec{p}_{rad} + \vec{r} \times \vec{p}_{perp} \ldotp \end{align*}\]

الحد الأول على اليمين هو صفر لأنه\(\vec{r}\) متوازي مع\(\vec{p}_{rad}\)، وفي الحد الثاني\(\vec{r}\) يكون عموديًا على\(\vec{p}_{perp}\)، لذلك ينخفض حجم الناتج المتقاطع إلى

\[L = rp_{perp} = rmv_{perp}.\]

لاحظ أن الزخم الزاوي لا يعتمد عليه\(p_{rad}\). نظرًا لأن قوة الجاذبية تكون في الاتجاه الشعاعي فقط، فإنها يمكن أن تتغير فقط\(p_{rad}\) ولا تتغير\(p_{perp}\)؛ وبالتالي، يجب أن يظل الزخم الزاوي ثابتًا.

الشكل\(\PageIndex{6}\): تم مسح عنصر المنطقة\(\Delta\) A في الوقت\(\Delta\) t بينما يتحرك الكوكب عبر الزاوية\(\Delta \phi\). الزاوية بين الاتجاه الشعاعي و\(\vec{v}\) is\(\theta\).

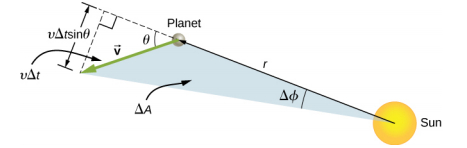
الآن فكر في الشكل\(\PageIndex{6}\). يتم مسح منطقة\(\Delta A\) مثلثة صغيرة بمرور الوقت\(\Delta t\). تقع السرعة على طول المسار وتشكل زاوية\(\theta\) بالاتجاه الشعاعي. ومن ثم، تُعطى السرعة العمودية بواسطة\(v_{perp}= v\sin \theta\). يتحرك الكوكب لمسافة\(\Delta\) s = v\(\Delta\) tin\(\theta\) مسقطة على طول الاتجاه عموديًا على\(r\). نظرًا لأن مساحة المثلث تساوي نصف القاعدة (\(r\)) مضروبة في الارتفاع (\(\Delta s\))، بالنسبة للإزاحة الصغيرة، يتم تحديد المساحة بواسطة

\[\Delta A = \frac{1}{2} r \Delta s. \nonumber\]

نحصل على\(\Delta s\) الاستبدال والضرب\(m\) في البسط والمقام وإعادة الترتيب

\[\Delta A = \frac{1}{2} r \Delta s = \frac{1}{2} r (v \Delta t \sin \theta) = \frac{1}{2m} r (mv \sin \theta \Delta t) = \frac{1}{2m} r (mv_{perp} \Delta t) = \frac{L}{2m} \Delta t \ldotp\]

السرعة المساحية هي ببساطة معدل تغير المنطقة مع مرور الوقت، لذلك لدينا

\[ \text{areal velocity} = \frac{\Delta A}{\Delta t} = \frac{L}{2m} \ldotp\]

نظرًا لأن الزخم الزاوي ثابت، يجب أن تكون سرعة المنطقة ثابتة أيضًا. هذا هو بالضبط قانون كيبلر الثاني. كما هو الحال مع قانون كيبلر الأول، أظهر نيوتن أنه نتيجة طبيعية لقانون الجاذبية الخاص به.

محاكاة

يمكنك مشاهدة نسخة متحركة من الشكل\(\PageIndex{6}\)، والعديد من الرسوم المتحركة الأخرى المثيرة للاهتمام أيضًا، في موقع كلية الفيزياء (جامعة نيو ساوث ويلز).

قانون كبلر الثالث

ينص قانون كبلر الثالث على أن مربع الفترة يتناسب مع مكعب المحور شبه الرئيسي للمدار. في مدارات الأقمار الصناعية والطاقة، استخلصنا قانون كيبلر الثالث للحالة الخاصة للمدار الدائري. تعطينا المعادلة\ ref {13.8} فترة مدار دائري نصف قطره r حول الأرض:

\[T = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} \ldotp \label{13.5.5}\]

بالنسبة للقطع الناقص، تذكر أن المحور شبه الرئيسي يساوي نصف مجموع الحضيض والإوج. بالنسبة للمدار الدائري، يكون المحور شبه الرئيسي (\(a\)) هو نفس نصف قطر المدار. في الواقع، تعطينا المعادلة\ ref {13.5.5} قانون كيبلر الثالث إذا قمنا ببساطة\(r\) باستبدال كلا الجانبين\(a\) وتربيعهما.

\[T^{2} = \frac{4 \pi^{2}}{GM} a^{3} \label{13.11}\]

لقد قمنا بتغيير كتلة الأرض إلى الأكثر عمومية\(M\)، حيث تنطبق هذه المعادلة على الأقمار الصناعية التي تدور حول أي كتلة كبيرة.

مثال\(\PageIndex{1}\): Orbit of Halley’s Comet

أوجد المحور شبه الرئيسي لمدار مذنب هالي، إذا كان يصل إلى الحضيض كل ٧٥٫٣ عامًا. إذا كان الحضيض 0.586 AU، فما هو الأوج؟

إستراتيجية

يتم إعطاؤنا الفترة، حتى نتمكن من إعادة ترتيب المعادلة\ ref {13.11}، وحل المحور شبه الرئيسي. نظرًا لأننا نعرف قيمة الحضيض، يمكننا استخدام تعريف المحور شبه الرئيسي، الموضح سابقًا في هذا القسم، للعثور على الأوج. نلاحظ أن 1 وحدة فلكية (AU) هي متوسط نصف قطر مدار الأرض ويتم تعريفها على أنها 1 AU = 1.50 × 10 ¹¹ m.

الحل

عند إعادة ترتيب المعادلة\ ref {13.11} وإدخال قيم فترة مذنب هالي وكتلة الشمس، لدينا

\[\begin{split} a & = \left(\dfrac{GM}{4 \pi^{2}} T^{2}\right)^{1/3} \\ & = \left(\dfrac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(2.00 \times 10^{30}\; kg)}{4 \pi^{2}} (75.3\; yr \times 365\; days/yr \times 24\; hr/day \times 3600\; s/hr)^{2}\right)^{1/3} \ldotp \end{split}\]

ينتج عن هذا قيمة 2.67 × 10 ¹² م أو 17.8 AU للمحور شبه الرئيسي. المحور شبه الرئيسي هو نصف مجموع الأوج والحضيض، لذلك لدينا

\[\begin{split} a & = \frac{1}{2} (aphelion + perihelion) \\ aphelion & = 2a - perihelion \ldotp \end{split}\]

وباستبدال القيم، وجدنا للمحور شبه الرئيسي والقيمة المعطاة للحضيض، أن قيمة الأوج هي 35.0 AU.

الدلالة

اشتبه إدموند هالي، أحد معاصري نيوتن، لأول مرة في أن ثلاثة مذنبات، تم الإبلاغ عنها في 1531 و 1607 و 1682، كانت في الواقع نفس المذنب. قبل أن يقوم Tycho Brahe بإجراء قياسات للمذنبات، كان يُعتقد أنها أحداث حدثت لمرة واحدة، وربما اضطرابات في الغلاف الجوي، وأنها لم تتأثر بالشمس. استخدم هالي ميكانيكا نيوتن الجديدة للتنبؤ بعودة المذنب الذي يحمل اسمه في عام 1758.

التمارين\(\PageIndex{1}\)

يبلغ متوسط نصف قطر مدار زحل الدائري تقريبًا حوالي 9.5 AU وتبلغ فترته 30 عامًا، بينما يبلغ متوسط أورانوس حوالي 19 AU وتبلغ فترته 84 عامًا. هل هذا يتفق مع نتائجنا لمذنب هالي؟