13.5: مدارات الأقمار الصناعية والطاقة
- Page ID
- 199911
- وصف آلية المدارات الدائرية
- ابحث عن الفترات المدارية وسرعات الأقمار الصناعية
- حدِّد ما إذا كانت الأجسام مرتبطة بالجاذبية
يدور القمر حول الأرض. في المقابل، تدور الأرض والكواكب الأخرى حول الشمس. تمتلئ المساحة الموجودة فوق غلافنا الجوي مباشرة بالأقمار الصناعية في المدار. ندرس أبسط هذه المدارات، المدار الدائري، لفهم العلاقة بين سرعة وفترة الكواكب والأقمار الصناعية فيما يتعلق بمواقعها والأجسام التي تدور حولها.
مدارات دائرية
كما لوحظ في بداية هذا الفصل، اقترح نيكولاوس كوبرنيكوس أولاً أن تدور الأرض وجميع الكواكب الأخرى حول الشمس في دوائر. وأشار كذلك إلى أن الفترات المدارية تزداد مع المسافة من الشمس. أظهر التحليل اللاحق الذي أجراه كيبلر أن هذه المدارات هي في الواقع أشكال بيضاوية، لكن مدارات معظم الكواكب في المجموعة الشمسية دائرية تقريبًا. تتراوح المسافة المدارية للأرض من الشمس بنسبة 2٪ فقط. الاستثناء هو مدار عطارد الغريب، الذي تتراوح مسافته المدارية بنسبة 40٪ تقريبًا.
إن تحديد السرعة المدارية والفترة المدارية للقمر الصناعي أسهل بكثير بالنسبة للمدارات الدائرية، لذلك نقوم بهذا الافتراض في الاشتقاق التالي. كما وصفنا في القسم السابق، فإن الجسم ذي الطاقة الإجمالية السالبة مرتبط بالجاذبية وبالتالي فهو في المدار. سيؤكد حسابنا للحالة الخاصة للمدارات الدائرية هذا. نحن نركز على الأجسام التي تدور حول الأرض، ولكن يمكن تعميم نتائجنا في حالات أخرى.
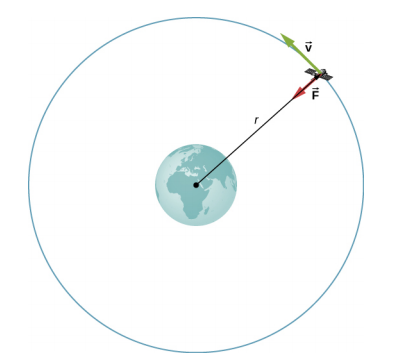
خذ بعين الاعتبار قمرًا صناعيًا كتلته m في مدار دائري حول الأرض على مسافة\(r\) من مركز الأرض (الشكل\(\PageIndex{1}\)). لديها تسارع مركزي موجه نحو مركز الأرض. جاذبية الأرض هي القوة الوحيدة المؤثرة، لذلك يعطي قانون نيوتن الثاني
\[\frac{GmM_{E}}{r^{2}} = ma_{c} = \frac{mv_{orbit}^{2}}{r} \ldotp\]
نقوم بحل سرعة المدار، مع ملاحظة الإلغاء\(m\)، للحصول على السرعة المدارية
\[v_{orbit} = \sqrt{\frac{GM_{E}}{r}} \ldotp \label{13.7}\]
بما يتفق مع ما رأيناه في\(g = G \frac{M_E}{r^2}\) و\(v_{esc} = \sqrt{\frac{2GM}{R}}\)، لا يظهر m في المعادلة\ ref {13.7}. تعتمد قيمة g وسرعة الهروب والسرعة المدارية فقط على المسافة من مركز الكوكب، وليس على كتلة الجسم الذي يتم العمل عليه. لاحظ التشابه في معادلات المدار v و v esc. سرعة الهروب أكبر\(\sqrt{2}\) بمرات بالضبط، حوالي 40٪، من السرعة المدارية. وقد لوحظت هذه المقارنة في المثال 13.4.2، وهي صحيحة بالنسبة للقمر الصناعي في أي دائرة نصف قطرها.
للعثور على فترة مدار دائري، نلاحظ أن القمر الصناعي يسافر حول محيط المدار\( 2\pi r\) في فترة واحدة\(T\). باستخدام تعريف السرعة، لدينا
\[v_{orbit} = \frac{2 \pi r}{T}.\]
نستبدل هذا بالمعادلة\ ref {13.7} ونعيد الترتيب للحصول عليه
\[T = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} \ldotp \label{13.8}\]
نرى في القسم التالي أن هذا يمثل قانون كيبلر الثالث لحالة المدارات الدائرية. كما تؤكد ملاحظة كوبرنيكوس أن فترة الكوكب تزداد مع زيادة المسافة من الشمس. نحتاج فقط إلى الاستبدال\(M_E\) بـ\(M_{Sun}\) في المعادلة\ ref {13.8}.
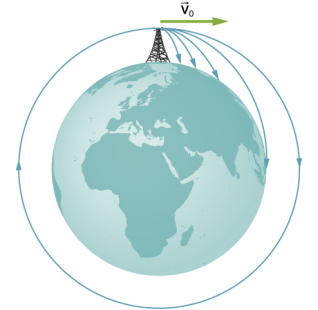
نختتم هذا القسم بالعودة إلى مناقشتنا السابقة حول رواد الفضاء في المدار الذين يبدو أنهم عديمي الوزن، كما لو كانوا يسقطون بحرية نحو الأرض. في الواقع، هم في حالة سقوط حر. ضع في اعتبارك المسارات الموضحة في الشكل\(\PageIndex{2}\). (يستند هذا الشكل إلى رسم لنيوتن في كتابه Principia وظهر أيضًا سابقًا في فيلم Motion in Two and Three Dimension.) جميع المسارات الموضحة التي تصل إلى سطح الأرض لها أقل من السرعة المدارية. سوف يتسارع رواد الفضاء نحو الأرض على طول المسارات غير الدائرية الموضحة ويشعرون بانعدام الوزن. (يتدرب رواد الفضاء فعليًا مدى الحياة في المدار من خلال ركوب الطائرات التي تسقط بحرية لمدة 30 ثانية في كل مرة.) ولكن مع السرعة المدارية الصحيحة، ينحني سطح الأرض بعيدًا عنها بنفس معدل هبوطها نحو الأرض. بالطبع، البقاء على نفس المسافة من السطح هو نقطة المدار الدائري.
يمكننا تلخيص مناقشتنا للأقمار الصناعية المدارية في استراتيجية حل المشكلات التالية.
- حدد ما إذا كانت معادلات السرعة أو الطاقة أو الفترة صالحة للمشكلة المطروحة. إذا لم يكن الأمر كذلك، فابدأ بالمبادئ الأولى التي استخدمناها لاشتقاق تلك المعادلات.
- للبدء من المبادئ الأولى، ارسم مخططًا للجسم الحر وقم بتطبيق قانون نيوتن للجاذبية وقانون نيوتن الثاني.
- إلى جانب تعريفات السرعة والطاقة، قم بتطبيق قانون نيوتن الثاني للحركة على الأجسام ذات الاهتمام.
حدد السرعة المدارية والفترة الزمنية لمحطة الفضاء الدولية (ISS).
إستراتيجية
نظرًا لأن محطة الفضاء الدولية تدور حول 4.00 × 10 × 2 كم فوق سطح الأرض، فإن نصف القطر الذي تدور فيه هو R E + 4.00 × 10 2 كم. نستخدم المعادلات\ ref {13.7} و\ ref {13.8} للعثور على السرعة المدارية والفترة، على التوالي.
الحل
باستخدام المعادلة\ ref {13.7}، تكون السرعة المدارية
\[v_{orbit} = \sqrt{\frac{GM_{E}}{r}} = \sqrt{\frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}{(6.36 \times 10^{6} + 4.00 \times 10^{5})\; m}} = 7.67 \times 10^{3}\; m/s\]
وهو ما يقرب من 17000 ميل بالساعة. باستخدام المعادلة\ ref {13.8}، تكون الفترة
\[T = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} = 2 \pi \sqrt{\frac{(6.36 \times 10^{6} + 4.00 \times 10^{5}\; m)^{3}}{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}} = 5.55 \times 10^{3}\; s\]
وهو ما يزيد قليلاً عن 90 دقيقة.
الأهمية
تعتبر محطة الفضاء الدولية في مدار أرضي منخفض (LEO). جميع الأقمار الصناعية تقريبًا موجودة في مدار أرضي منخفض، بما في ذلك معظم الأقمار الصناعية الخاصة تعتبر الأقمار الصناعية GPS، التي يبلغ طولها حوالي 20,000 كم، مدارًا أرضيًا متوسطًا. كلما ارتفع المدار، زادت الطاقة المطلوبة لوضعه هناك وزادت الحاجة إلى الطاقة للوصول إليه لإجراء الإصلاحات. تعتبر الأقمار الصناعية في المدار المتزامن مع الأرض ذات أهمية خاصة. جميع أطباق الأقمار الصناعية الثابتة على الأرض التي تشير إلى السماء، مثل أطباق استقبال التلفزيون، موجهة نحو الأقمار الصناعية المتزامنة مع الأرض. يتم وضع هذه الأقمار الصناعية على المسافة الدقيقة، وفوق خط الاستواء مباشرة، بحيث تكون فترة مدارها يومًا واحدًا. تبقى في وضع ثابت بالنسبة لسطح الأرض.
ما العامل الذي يجب أن يتغير به نصف القطر لتقليل السرعة المدارية للقمر الصناعي بمقدار النصف؟ بأي عامل سيغير هذا الفترة؟
أوجد كتلة الأرض من مدار القمر.
إستراتيجية
نستخدم المعادلة\ ref {13.8}، وحل M E، ونستبدل الفترة ونصف قطر المدار. تم قياس نصف قطر وفترة مدار القمر بدقة معقولة منذ آلاف السنين. من البيانات الفلكية في الملحق D، تبلغ فترة القمر 27.3 يومًا = 2.36 × 10 6 ثوانٍ، ويبلغ متوسط المسافة بين مراكز الأرض والقمر 384000 كم.
الحل
حل لـ\(M_E\)،
\[\begin{split} T & = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} \\ M_{E} & = \frac{2 \pi^{2} r^{3}}{GT^{2}} = \frac{4 \pi^{2} (3.84 \times 10^{8}\; m)^{3}}{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(2.36 \times 10^{6}\; s)^{2}} = 6.01 \times 10^{24}\; kg \ldotp \end{split}\]
الأهمية
قارن ذلك بقيمة 5.96 × 10 24 كجم التي حصلنا عليها في المثال 13.3.3، باستخدام القيمة\(g\) على سطح الأرض. على الرغم من أن هذه القيم قريبة جدًا (~ 0.8٪)، فإن كلا الحسابين يستخدمان القيم المتوسطة. تختلف قيمة g من خط الاستواء إلى القطبين بنسبة 0.5٪ تقريبًا. لكن القمر يحتوي على مدار بيضاوي الشكل حيث تختلف قيمة r بنسبة تزيد قليلاً عن 10٪. (يختلف الحجم الظاهري للقمر الكامل فعليًا بهذه الكمية تقريبًا، ولكن من الصعب ملاحظة ذلك من خلال الملاحظة العرضية حيث أن الوقت من طرف إلى آخر هو عدة أشهر.)
هناك اعتبار آخر لهذا الحساب الأخير لـ M E. لقد اشتقنا المعادلة\ ref {13.8} بافتراض أن القمر الصناعي يدور حول مركز الجسم الفلكي في نفس نصف القطر المستخدم في التعبير عن قوة الجاذبية بينهما. ما الافتراض الذي يتم تقديمه لتبرير ذلك؟ تبلغ مساحة الأرض حوالي 81 مرة أكبر من القمر. هل يدور القمر حول المركز الدقيق للأرض؟
دعونا نعيد النظر في المثال 13.2.2. افترض أن مجرات درب التبانة وأندروميدا في مدار دائري حول بعضها البعض. ماذا ستكون سرعة كل منها وكم ستكون مدتها المدارية؟ لنفترض أن كتلة كل منها تبلغ 800 مليار كتلة شمسية وأن مراكزها مفصولة بـ 2.5 مليون سنة ضوئية.
إستراتيجية
لا يمكننا استخدام المعادلات\ ref {13.7} و\ ref {13.8} مباشرةً لأنها مشتقة بافتراض أن جسم الكتلة m يدور حول مركز كوكب أكبر بكثير كتلته M. لقد حددنا قوة الجاذبية في المثال 13.2.2 باستخدام قانون نيوتن للجاذبية العامة. يمكننا استخدام قانون نيوتن الثاني، المطبق على التسارع المركزي لأي من المجرات، لتحديد سرعتها العرضية. من هذه النتيجة يمكننا تحديد فترة المدار.
الحل
في المثال 13.2.2، وجدنا القوة بين المجرات
\[F_{12} = G \frac{m_{1} m_{2}}{r^{2}} = (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})\frac{[(800 \times 10^{9})(2.0 \times 10^{30})\; kg]^{2}}{[(2.5 \times 10^{6})(9.5 \times 10^{15})\; m]^{2}} = 3.0 \times 10^{29}\; N\]
وأن تسارع كل مجرة هو
\[a = \frac{F}{m} = \frac{3.0 \times 10^{29}\; N}{(800 \times 10^{9})(2.0 \times 10^{30})\; kg} = 1.9 \times 10^{-13}\; m/s^{2} \ldotp\]
نظرًا لوجود المجرات في مدار دائري، فإنها تتمتع بالتسارع المركزي. إذا تجاهلنا تأثير المجرات الأخرى، فعندئذٍ، كما تعلمنا في الزخم الخطي والاصطدامات ودوران المحور الثابت، تظل مراكز كتلة المجرتين ثابتة. ومن ثم، يجب أن تدور المجرات حول مركز الكتلة المشترك هذا. بالنسبة للكتل المتساوية، يكون مركز الكتلة بالضبط في منتصف الطريق بينهما. لذا فإن نصف قطر المدار، أو المدار، ليس هو نفس المسافة بين المجرات، ولكن نصف هذه القيمة، أو 1.25 مليون سنة ضوئية. تظهر هاتان القيمتان المختلفتان في الشكل\(\PageIndex{3}\).

باستخدام تعبير التسارع المركزي، لدينا
\[\begin{split} a_{c} & = \frac{v_{orbit}^{2}}{r_{orbit}} \\ 1.9 \times 10^{-13}\; m/s^{2} & = \frac{v_{orbit}^{2}}{(1.25 \times 10^{6})(9.5 \times 10^{15})\; m} \ldotp \end{split}\]
لدينا حل لسرعة المدار\(v_{orbit} = 47\, km/s\). أخيرًا، يمكننا تحديد فترة المدار مباشرة من
\[T = \frac{2 \pi r}{v_{orbit}}\]
لتجد أن الفترة هي T = 1.6 × 10 18 ثانية، أي حوالي 50 مليار سنة.
الأهمية
قد تبدو السرعة المدارية البالغة 47 كم/ثانية عالية في البداية. لكن هذه السرعة يمكن مقارنتها بسرعة الهروب من الشمس، والتي قمنا بحسابها في مثال سابق. لإعطاء المزيد من المنظور، فإن هذه الفترة أطول بأربع مرات تقريبًا من الوقت الذي كان فيه الكون موجودًا.
في الواقع، فإن الحركة النسبية الحالية لهاتين المجرتين من المتوقع أن تصطدم في حوالي 4 مليارات سنة. على الرغم من أن كثافة النجوم في كل مجرة تجعل الاصطدام المباشر لأي نجمين أمرًا غير محتمل، فإن مثل هذا التصادم سيكون له تأثير كبير على شكل المجرات. أمثلة مثل هذه التصادمات معروفة جيدًا في علم الفلك.
المجرات ليست كائنات مفردة. كيف تقارن قوة جاذبية إحدى المجرات المؤثرة على النجوم «الأقرب» للمجرة الأخرى بتلك البعيدة؟ ما تأثير ذلك على شكل المجرات نفسها؟
راجع صفحة مسح سلون الرقمي للسماء لمزيد من المعلومات حول المجرات المتصادمة.
استخدم هذه المحاكاة التفاعلية لتحريك الشمس والأرض والقمر ومحطة الفضاء لرؤية التأثيرات على قوى الجاذبية والمسارات المدارية. تخيل الأحجام والمسافات بين الأجسام السماوية المختلفة، وأطفئ الجاذبية لترى ما سيحدث بدونها.
الطاقة في المدارات الدائرية
في الطاقة الكامنة للجاذبية والطاقة الكلية، جادلنا بأن الأجسام مرتبطة بالجاذبية إذا كانت طاقتها الإجمالية سالبة. استندت الحجة إلى الحالة البسيطة حيث كانت السرعة بعيدة مباشرة أو باتجاه الكوكب. نفحص الآن الطاقة الكلية لمدار دائري ونوضح أن الطاقة الكلية سالبة بالفعل. كما فعلنا سابقًا، نبدأ بقانون نيوتن الثاني المطبق على مدار دائري،
\[\begin{split} \frac{GmM_{E}}{r^{2}} & = ma_{c} = \frac{mv^{2}}{r} \\ \frac{GmM_{E}}{r} & = mv^{2} \ldotp \end{split}\]
في الخطوة الأخيرة، ضربنا\(r\) في كل جانب. الجانب الأيمن هو ضعف الطاقة الحركية فقط، لذلك لدينا
\[K = \frac{1}{2} mv^{2} = \frac{GmM_{E}}{2r} \ldotp\]
الطاقة الكلية هي مجموع الطاقات الحركية والمحتملة، لذا فإن النتيجة النهائية هي
\[E = K + U = \frac{GmM_{E}}{2r} - \frac{GmM_{E}}{r} = - \frac{GmM_{E}}{2r} \ldotp \label{13.9}\]
يمكننا أن نرى أن الطاقة الكلية سالبة، بنفس حجم الطاقة الحركية. بالنسبة للمدارات الدائرية، يبلغ حجم الطاقة الحركية بالضبط نصف حجم الطاقة الكامنة. ومن اللافت للنظر أن هذه النتيجة تنطبق على أي كتلتين في مدارات دائرية حول مركز الكتلة المشترك بينهما، على مسافة أو عن بعضهما البعض. يتم ترك الدليل على ذلك كتمرين. سنرى في القسم التالي أن تعبيرًا مشابهًا جدًا ينطبق في حالة المدارات البيضاوية.
في المثال 13.4.1، قمنا بحساب الطاقة المطلوبة لمجرد رفع مركبة سويوز التي تزن 900 كجم من سطح الأرض إلى ارتفاع محطة الفضاء الدولية، 400 كم فوق سطح الأرض. بعبارة أخرى، وجدنا تغيرها في الطاقة الكامنة. نسأل الآن، ما هو إجمالي تغير الطاقة في مركبة سويوز المطلوب لأخذها من سطح الأرض ووضعها في المدار مع محطة الفضاء الدولية من أجل الالتقاء (الشكل\(\PageIndex{4}\))؟ ما مقدار طاقة الحركة من إجمالي هذه الطاقة؟
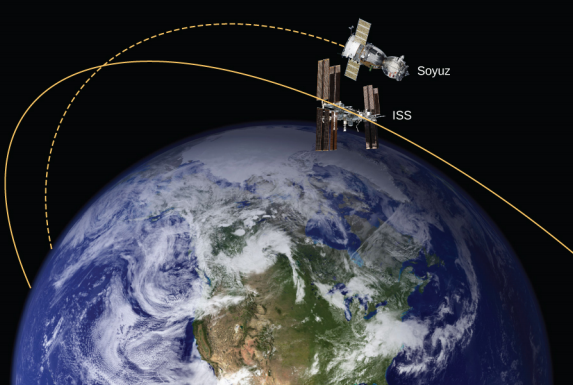
إستراتيجية
الطاقة المطلوبة هي الفرق في إجمالي طاقة Soyuz في المدار وتلك الموجودة على سطح الأرض. يمكننا استخدام Equation\ ref {13.9} لإيجاد الطاقة الكلية لسويوز في مدار محطة الفضاء الدولية. لكن الطاقة الإجمالية على السطح هي ببساطة الطاقة الكامنة، لأنها تبدأ من الراحة. [لاحظ أننا لا نستخدم المعادلة\ ref {13.9} على السطح، لأننا لسنا في مدار على السطح.] يمكن بعد ذلك العثور على الطاقة الحركية من الفرق في إجمالي تغير الطاقة والتغير في الطاقة الكامنة الموجود في المثال 13.4.1. بدلاً من ذلك، يمكننا استخدام المعادلة\ ref {13.7} لإيجاد مدار v وحساب الطاقة الحركية مباشرة من ذلك. الطاقة الإجمالية المطلوبة هي الطاقة الحركية بالإضافة إلى التغيير في الطاقة الكامنة الموجودة في المثال 13.4.1.
الحل
من المعادلة\ ref {13.9}، تكون الطاقة الكلية لسويوز في نفس مدار محطة الفضاء الدولية
\[\begin{split} E_{orbit} & = K_{orbit} + U_{orbit} = - \frac{GmM_{E}}{2r} \\ & = \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(9000\; kg)(5.96 \times 10^{24}\; kg)}{2(6.36 \times 10^{6} + 4.00 \times 10^{5}\; m)} = -2.65 \times 10^{11}\; J \ldotp \end{split}\]
إجمالي الطاقة على سطح الأرض
\[\begin{split} E_{surface} & = K_{surface} + U_{surface} = 0 - \frac{GmM_{E}}{r} \\ & = - \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(9000\; kg)(5.96 \times 10^{24}\; kg)}{(6.36 \times 10^{6}\; m)} \\ & = -5.63 \times 10^{11}\; J \ldotp \end{split}\]
التغيير في الطاقة هو
\[\Delta E = E_{orbit}− E_{surface} = 2.98 x 10^{11}\, J. \nonumber\]
للحصول على الطاقة الحركية، نطرح التغير في الطاقة الكامنة من المثال 13.4.1،\(\Delta\) U = 3.32 × 10 10 J. وهذا يعطينا مدار K = (2.98 × 10 11) - (3.32 × 10 10) = 2.65 × 10 11 J. كما ذكرنا سابقًا، فإن الطاقة الحركية يكون المدار الدائري دائمًا نصف حجم الطاقة الكامنة، ونفس حجم الطاقة الكلية. نتائجنا تؤكد ذلك.
الطريقة الثانية هي استخدام المعادلة\ ref {13.7} للعثور على السرعة المدارية لسويوز، وهو ما فعلناه لمحطة الفضاء الدولية في المثال\(\PageIndex{1}\).
\[ \begin{align*} v_{orbit} &= \sqrt{\frac{GM_{E}}{r}} \\[4pt]&= \sqrt{\frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}{(6.36 \times 10^{6} + 4.00 \times 10^{5})\; m}} \\[4pt] &= 7.67 \times 10^{3}\; m/s \end{align*}\]
إذن الطاقة الحركية لسويوز في المدار هي
\[ \begin{align*}K_{orbit} &= \frac{1}{2} mv_{orbit}^{2} \\[4pt]&= \frac{1}{2} (9000\; kg)(7.67 \times 10^{3}\; m/s)^{2} \\[4pt]&= 2.65 \times 10^{11}\; J,\end{align*}\]
نفس الطريقة السابقة. الطاقة الإجمالية هي فقط
\[ \begin{align*}E_{orbit} &= K_{orbit} + \Delta U \\[4pt]&= (2.65 \times 10^{11}) + (3.32 \times 10^{10}) \\[4pt]&= 2.95 \times 10^{11}\; J \ldotp\end{align*}\]
الأهمية
تبلغ الطاقة الحركية لسويوز ما يقرب من ثمانية أضعاف التغيير في طاقتها الكامنة، أو 90٪ من إجمالي الطاقة اللازمة للالتقاء مع محطة الفضاء الدولية. ومن المهم أن نتذكر أن هذه الطاقة لا تمثل سوى الطاقة التي يجب إعطاؤها لـ Soyuz. بفضل تكنولوجيا الصواريخ الحالية لدينا، تتجاوز كتلة نظام الدفع (وقود الصواريخ وحاوياته ونظام الاحتراق) بكثير كتلة الحمولة، ويجب إعطاء كمية هائلة من الطاقة الحركية لتلك الكتلة. لذا فإن التكلفة الفعلية للطاقة هي عدة أضعاف تكلفة التغيير في طاقة الحمولة نفسها.


