13.4: طاقة وضع الجاذبية والطاقة الكلية

Last updated
Save as PDF

Page ID: 199917

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

أهداف التعلم

حدِّد التغيُّرات في طاقة وضع الجاذبية عبر مسافات كبيرة
تطبيق الحفاظ على الطاقة لتحديد سرعة الهروب
حدد ما إذا كانت الأجسام الفلكية مرتبطة بالجاذبية

درسنا طاقة الجاذبية الكامنة في الطاقة الكامنة والحفاظ على الطاقة، حيث\(g\) ظلت قيمتها ثابتة. نقوم الآن بتطوير تعبير يعمل عبر مسافات بحيث لا يكون g ثابتًا. يعد ذلك ضروريًا لحساب الطاقة اللازمة لوضع الأقمار الصناعية في المدار بشكل صحيح أو لإرسالها في مهمات في الفضاء.

طاقة الجاذبية الكامنة وراء الأرض

لقد حددنا العمل والطاقة المحتملة سابقًا. فائدة هذه التعريفات هي السهولة التي يمكننا بها حل العديد من المشكلات باستخدام الحفاظ على الطاقة. الطاقة الكامنة مفيدة بشكل خاص للقوى التي تتغير مع الموضع، كما تفعل قوة الجاذبية عبر مسافات كبيرة. في الطاقة الكامنة والحفاظ على الطاقة، أظهرنا أن التغيير في طاقة الجاذبية الكامنة بالقرب من سطح الأرض هو

\[ \Delta U = mg(y_2− y_1) \label{simple}\]

يعمل هذا جيدًا إذا لم\(g\) يتغير بشكل كبير بين y ₁ و y ₂. نعود إلى تعريف العمل والطاقة الكامنة لاشتقاق تعبير صحيح عبر مسافات أكبر. تذكر أن العمل (W) هو جزء لا يتجزأ من منتج النقاط بين القوة والمسافة. في الأساس، هو نتاج مكون القوة على طول أوقات النزوح. نحدد العمل\(\Delta u\) الذي تقوم به القوة التي نربطها بالطاقة الكامنة على أنه سلبي. من أجل الوضوح، نشتق تعبيرًا لتحريك كتلة m من المسافة r ₁ من مركز الأرض إلى المسافة r ₂. ومع ذلك، يمكن تعميم النتيجة بسهولة على أي كائنين بتغيير فصلهما من قيمة إلى أخرى.

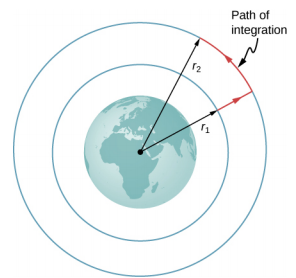
رسم توضيحي للأرض ودائرتين أكبر متحدة المركز تتمركز حولها. يُطلق على نصف قطر الدائرة الصغيرة اسم r 1 بسهم أسود ونصف قطر الدائرة الأكبر بـ r 2 بسهم أسود. يمتد السهم الأحمر من نهاية السهم r 1 إلى الدائرة الأكبر، ثم يشكل قوسًا على الدائرة الأكبر إلى طرف السهم r 2. يُطلق على الخط الأحمر اسم مسار التكامل. — الشكل\(\PageIndex{1}\): يمكن تقييم تكامل العمل، الذي يحدد التغيير في الطاقة الكامنة، على طول المسار الموضح باللون الأحمر.

ضع في اعتبارك الشكل\(\PageIndex{1}\) الذي نأخذ فيه m من مسافة r ₁ من مركز الأرض إلى مسافة r ₂ من المركز. الجاذبية هي قوة محافظة (حجمها واتجاهها هي وظائف الموقع فقط)، لذلك يمكننا اتخاذ أي مسار نرغب فيه، والنتيجة لحساب العمل هي نفسها. نأخذ المسار الموضح، لأنه يبسط التكامل بشكل كبير. نتحرك أولاً شعاعيًا للخارج من المسافة r ₁ إلى المسافة r ₂، ثم نتحرك على طول قوس الدائرة حتى نصل إلى الموضع النهائي. خلال الجزء الشعاعي،\(\vec{F}\) يكون معاكسًا للاتجاه الذي نسير فيه على طول d\(\vec{r}\)، لذلك

\[E = K_1 + U_1 = K_2 + U_2\]

على طول القوس،\(\vec{F}\) يكون عموديًا على d\(\vec{r}\)، لذلك\(\vec{F}\; \cdotp d \vec{r}\) = 0. لا يتم إنجاز أي عمل بينما نتحرك على طول القوس. باستخدام تعبير قوة الجاذبية وملاحظة القيم الموجودة على\(\vec{F}\; \cdotp d \vec{r}\) طول مقطعي مسارنا، لدينا

\[ \begin{align} \Delta U &= - \int_{r_{1}}^{r_{2}} \vec{F}\; \cdotp d \vec{r} \\[4pt] &= GM_{E} m \int_{r_{1}}^{r_{2}} \frac{dr}{r^{2}} \\[4pt] &= GM_{E} m \left(\dfrac{1}{r_{1}} - \dfrac{1}{r_{2}}\right) \ldotp \label{eq13.3} \end{align} \]

نظرًا لأنه\(\Delta U = U_2 − U_1\) يمكننا اعتماد تعبير بسيط لـ\(U\):

\[U = - \frac{GM_{E} m}{r} \ldotp \label{13.4}\]

لاحظ عنصرين مهمين بهذا التعريف. أولاً،\(U → 0\) مثل\(r → \infty\). تكون الطاقة الكامنة صفرًا عندما تكون الكتلتين متباعدتين بشكل لا نهائي. الفرق الوحيد\(U\) هو المهم، لذا فإن اختيار\(U = 0\) النموذج\(r = \infty\) هو مجرد اختيار للراحة. (تذكر أنه في مشاكل الجاذبية السابقة، كان بإمكانك أخذها\(U = 0\) إلى أعلى أو أسفل المبنى، أو في أي مكان.) ثانيًا، لاحظ أن\(U\) الأمر يصبح أكثر سلبية بشكل متزايد مع اقتراب الجماهير. وهذا يتفق مع ما تعلمته عن الطاقة الكامنة في الطاقة المحتملة والحفاظ على الطاقة. عندما يتم فصل الكتلتين، يجب القيام بعمل إيجابي ضد قوة الجاذبية، وبالتالي\(U\) يزداد (يصبح أقل سلبية). تسقط جميع الكتل بشكل طبيعي معًا تحت تأثير الجاذبية، وتنخفض من طاقة ذات جهد أعلى إلى طاقة منخفضة.

مثال\(\PageIndex{1}\): Lifting a Payload

ما مقدار الطاقة المطلوبة لرفع مركبة سويوز التي تزن 900 كجم من سطح الأرض إلى ارتفاع محطة الفضاء الدولية، أي 400 كم فوق سطح الأرض؟

إستراتيجية

استخدم المعادلة\ ref {eq13.3} للعثور على التغيير في الطاقة الكامنة للحمولة. يجب توفير هذا القدر من العمل أو الطاقة لرفع الحمولة.

الحل

مع الانتباه إلى حقيقة أننا نبدأ من سطح الأرض وننتهي عند 400 كم فوق السطح، فإن التغيير في\(U\)

\[ \begin {align*} \Delta U &= U_{orbit} - U_{Earth} \\[4pt] &= - \dfrac{GM_{E} m}{R_{E} + 400\; km} - \left(- \dfrac{GM_{E} m}{R_{E}}\right) \ldotp \end{align*}\]

نقوم بإدراج القيم

\(m = 9000\; kg\)
\(M_{E} = 5.96 \times 10^{24}\; kg\)
\(R_{E} = 6.37 \times 10^{6}\; m\)

ونحول 400 كم إلى 4.00 × 10 ⁵ م، نجد\(\Delta U = 3.32 \times 10^{10} J\). إنه أمر إيجابي، مما يشير إلى زيادة الطاقة المحتملة، كما نتوقع.

الأهمية

من منظور، ضع في اعتبارك أن متوسط استخدام الطاقة المنزلية في الولايات المتحدة في عام 2013 كان 909 كيلووات في الساعة شهريًا. هذه هي طاقة

\[909\; kWh \times 1000\; W/kW \times 3600\; s/h = 3.27 \times 10^{9}\; J\; per\; month \ldotp \nonumber\]

لذا فإن نتيجتنا هي إنفاق طاقة يعادل 10 أشهر. ومع ذلك، هذه هي الطاقة اللازمة لرفع الحمولة 400 كم. إذا أردنا أن تكون مركبة Soyuz في المدار حتى تتمكن من الالتقاء بمحطة الفضاء الدولية وليس مجرد العودة إلى الأرض، فإنها تحتاج إلى الكثير من الطاقة الحركية. كما نرى في القسم التالي، تبلغ الطاقة الحركية حوالي خمسة أضعاف طاقة\(\Delta\) U. بالإضافة إلى ذلك، يتم إنفاق المزيد من الطاقة لرفع نظام الدفع نفسه. السفر إلى الفضاء ليس رخيصًا.

التمارين الرياضية\(\PageIndex{1}\)

لماذا لا تستخدم التعبير الأبسط في المعادلة\ ref {simple} بدلاً من ذلك؟ ما مدى أهمية الخطأ؟ (القيمة\(g\) عند 400 كم فوق الأرض هي 8.67 م/ث ².)

الحفاظ على الطاقة

في الطاقة المحتملة والحفاظ على الطاقة، وصفنا كيفية تطبيق الحفاظ على الطاقة للأنظمة ذات القوى المحافظة. لقد تمكنا من حل العديد من المشكلات، خاصة تلك المتعلقة بالجاذبية، ببساطة باستخدام الحفاظ على الطاقة. تنطبق هذه المبادئ واستراتيجيات حل المشكلات بشكل جيد هنا. التغيير الوحيد هو وضع التعبير الجديد للطاقة الكامنة في معادلة الحفاظ على الطاقة،

\[E_{tot} = K_1 + U_1 = K_2 + U_2.\]

\[\frac{1}{2} mv_{1}^{2} - \frac{GMm}{r_{1}} = \frac{1}{2} mv_{2}^{2} - \frac{GMm}{r_{2}} \label{13.5}\]

لاحظ أننا نستخدم M، بدلاً من M _E، كتذكير بأننا لا نقتصر على المشاكل المتعلقة بالأرض. ومع ذلك، ما زلنا نفترض أن m << M. (بالنسبة للمشكلات التي لا يكون فيها هذا صحيحًا، نحتاج إلى تضمين الطاقة الحركية لكلتا الكتلتين واستخدام الحفاظ على الزخم لربط السرعات ببعضها البعض. لكن المبدأ لا يزال هو نفسه.)

سرعة الهروب

غالبًا ما يتم تعريف سرعة الهروب على أنها الحد الأدنى للسرعة الأولية لجسم مطلوب للهروب من سطح كوكب (أو أي جسم كبير مثل القمر) وعدم العودة أبدًا. كالعادة، نفترض عدم فقدان أي طاقة في الغلاف الجوي، في حالة وجود أي طاقة.

ضع في اعتبارك الحالة التي يتم فيها إطلاق جسم من سطح كوكب بسرعة أولية موجهة بعيدًا عن الكوكب. مع الحد الأدنى من السرعة اللازمة للهروب، سيستريح الجسم بعيدًا إلى ما لا نهاية، أي أن الجسم يتخلى عن آخر طاقته الحركية بمجرد وصوله إلى اللانهاية، حيث تصبح قوة الجاذبية صفرًا. نظرًا لأن U → 0 كـ r →\(\infty\)، فهذا يعني أن الطاقة الإجمالية هي صفر. وهكذا نجد سرعة الهروب من سطح جسم فلكي كتلته M ونصف قطره R عن طريق تحديد الطاقة الكلية التي تساوي الصفر. على سطح الجسم، يقع الجسم عنده\(r_1 = R\) ولديه سرعة هروب\(v_1 = v_{esc}\). تصل\(r_2 = \infty\) بسرعة\(v_2 = 0\). بالاستعاضة عن المعادلة\ المرجع {13.5}، لدينا

\[\frac{1}{2} mv_{esc}^{2} - \frac{GMm}{R} = \frac{1}{2} m0^{2} - \frac{GMm}{\infty} = 0 \ldotp\]

حل سرعة الهروب،

\[v_{esc} = \sqrt{\frac{2GM}{R}} \ldotp \label{13.6}\]

لاحظ أنه\(m\) تم إلغاؤه خارج المعادلة. سرعة الهروب هي نفسها لجميع الكائنات، بغض النظر عن الكتلة. كما أننا لا نقتصر على سطح الكوكب؛ يمكن أن تكون R أي نقطة انطلاق خارج سطح الكوكب.

مثال\(\PageIndex{2}\): Escape from Earth

ما سرعة الهروب من سطح الأرض؟ افترض عدم وجود فقدان للطاقة بسبب مقاومة الهواء. قارن ذلك بسرعة الهروب من الشمس، بدءًا من مدار الأرض.

إستراتيجية

نستخدم المعادلة 13.6، التي تحدد بوضوح قيم R و M. للهروب من الأرض، نحتاج إلى كتلة ونصف قطر الأرض. للهروب من الشمس، نحتاج إلى كتلة الشمس والمسافة المدارية بين الأرض والشمس.

الحل

باستبدال قيم كتلة الأرض ونصف قطرها مباشرة في المعادلة 13.6، نحصل على

\[ \begin {align*} v_{esc} &= \sqrt{\frac{2GM}{R}} \\[4pt] &= \sqrt{\frac{2 (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}{6.37 \times 10^{6}\; m}} \\[4pt] &= 1.12 \times 10^{4}\; m/s \ldotp \end{align*}\]

أي حوالي 11 كم/ثانية أو 25000 ميل في الساعة. للهروب من الشمس، بدءًا من مدار الأرض، نستخدم R = R _ES = 1.50 × 10 ¹¹ م و M _Sun = 1.99 × 10 ³⁰ كجم. والنتيجة هي v _esc = 4.21 × 10 ⁴ م/ث أو حوالي 42 كم/ثانية.

الأهمية

تبلغ السرعة اللازمة للهروب من الشمس (مغادرة النظام الشمسي) ما يقرب من أربعة أضعاف سرعة الهروب من سطح الأرض. ولكن هناك مساعدة في كلتا الحالتين. تدور الأرض بسرعة تقارب 1.7 كم/ثانية عند خط الاستواء، ويمكننا استخدام هذه السرعة للمساعدة في الهروب، أو للوصول إلى المدار. لهذا السبب، تحتفظ العديد من شركات الفضاء التجارية بمرافق الإطلاق بالقرب من خط الاستواء. للهروب من الشمس، هناك المزيد من المساعدة. تدور الأرض حول الشمس بسرعة تقارب 30 كم/ثانية، ومن خلال الإطلاق في الاتجاه الذي تتحرك فيه الأرض، نحتاج فقط إلى 12 كم/ثانية إضافية، واستخدام مساعدة الجاذبية من الكواكب الأخرى، وهي في الأساس تقنية مقلاع الجاذبية، يسمح للمسبار الفضائية بالوصول إلى سرعات أكبر. في تقنية المقلاع هذه، تقترب المركبة من الكوكب ويتم تسريعها من خلال جاذبية الكوكب. وتبلغ سرعتها القصوى عند أقرب نقطة في الاقتراب، على الرغم من أنها تتباطأ بنفس القدر مع ابتعادها. ولكن بالنسبة إلى الكوكب، فإن سرعة السيارة قبل الاقتراب بكثير، وبعدها بفترة طويلة، هي نفسها. إذا تم اختيار الاتجاهات بشكل صحيح، فقد يؤدي ذلك إلى زيادة كبيرة (أو انخفاض إذا لزم الأمر) في سرعة السيارة مقارنة ببقية النظام الشمسي.

الطاقة والأجسام المرتبطة بالجاذبية

كما ذكرنا سابقًا، يمكن تعريف سرعة الهروب على أنها السرعة الأولية لجسم يمكنه الهروب من سطح القمر أو الكوكب. بشكل عام، هي السرعة في أي موضع بحيث تكون الطاقة الإجمالية صفرًا. إذا كانت الطاقة الإجمالية صفرًا أو أكثر، يهرب الكائن. إذا كانت الطاقة الكلية سالبة، فلن يتمكن الكائن من الهروب. دعونا نرى لماذا هذا هو الحال.

كما ذكرنا سابقًا، نرى ذلك على\(U → 0\) النحو التالي\(r → \infty\). إذا كانت الطاقة الكلية صفرًا، فعندما تصل m إلى قيمة r تقترب من اللانهاية، تصبح U صفرًا وكذلك الطاقة الحركية. وبالتالي، يستقر m بعيدًا بشكل لا نهائي عن M. لقد «نجا للتو» M. إذا كانت الطاقة الكلية موجبة، فإن الطاقة الحركية تظل عند المستوى\(r = \infty\) وبالتأكيد لا تعود m. عندما تكون الطاقة الكلية صفرًا أو أكثر، فإننا نقول إن m غير مرتبط بالجاذبية بـ M.

من ناحية أخرى، إذا كانت الطاقة الكلية سالبة، فيجب أن تصل الطاقة الحركية إلى الصفر عند بعض القيمة المحدودة لـ r، حيث تكون U سالبة وتساوي الطاقة الكلية. لا يمكن للجسم أبدًا تجاوز هذه المسافة المحدودة من M، لأن القيام بذلك يتطلب أن تصبح الطاقة الحركية سالبة، وهو أمر غير ممكن. نقول أن m مرتبط بالجاذبية بـ M.

لقد قمنا بتبسيط هذه المناقشة من خلال افتراض أن الكائن كان متجهًا بعيدًا مباشرة عن الكوكب. اللافت للنظر هو أن النتيجة تنطبق على أي سرعة. الطاقة هي كمية قياسية، وبالتالي فإن المعادلة\ ref {13.5} هي معادلة عددية - لا يلعب اتجاه السرعة أي دور في الحفاظ على الطاقة. من الممكن أن يكون هناك نظام مرتبط بالجاذبية حيث لا «تسقط الكتل معًا»، ولكنها تحافظ على الحركة المدارية حول بعضها البعض.

لدينا ملاحظة أخيرة مهمة. ذكرنا سابقًا أنه إذا كانت الطاقة الإجمالية صفرًا أو أكثر، فإن الكائن يهرب. بالمعنى الدقيق للكلمة، تنطبق المعادلة\ المرجع {13.5} والمعادلة\ المرجع {13.6} على كائنات النقاط. تنطبق أيضًا على الأجسام ذات الحجم المحدود والمتناظر كرويًا، بشرط أن تكون القيمة\(r\) في المعادلة\ ref {13.5} دائمًا أكبر من مجموع أنصاف أقطار الجسمين. إذا أصبح r أقل من هذا المجموع، فإن الكائنات تصطدم. (حتى بالنسبة للقيم الأكبر لـ r، ولكن بالقرب من مجموع أنصاف الأقطار، يمكن لقوى المد والجزر الجاذبية أن تخلق تأثيرات كبيرة إذا كان كلا الجسمين بحجم الكوكب. ندرس تأثيرات المد والجزر في قوى المد والجزر.) لا تمنع الطاقة الإجمالية الإيجابية أو السلبية الكتل ذات الحجم المحدود من الاصطدام. بالنسبة للأشياء الحقيقية، يكون الاتجاه مهمًا.

مثال\(\PageIndex{3}\): How Far Can an Object Escape?

لننظر في المثال السابق مرة أخرى، حيث قمنا بحساب سرعة الهروب من الأرض والشمس، بدءًا من مدار الأرض. لاحظنا أن الأرض تبلغ سرعتها المدارية بالفعل 30 كم/ثانية، وكما نرى في القسم التالي، هذه هي السرعة العرضية اللازمة للبقاء في مدار دائري. إذا كان جسم ما بهذه السرعة على مسافة مدار الأرض، لكنه اتجه بعيدًا عن الشمس مباشرةً، فما المسافة التي سيقطعها قبل أن يستريح؟ تجاهل تأثيرات الجاذبية لأي أجسام أخرى.

إستراتيجية

يحتوي الجسم على طاقات حركية وطاقات محتملة أولية يمكننا حسابها. عندما تصل سرعته إلى الصفر، يكون في أقصى مسافة من الشمس. نستخدم المعادلة 13.5، حفظ الطاقة، لإيجاد المسافة التي تساوي عندها طاقة الحركة صفرًا.

الحل

الموضع الأولي للجسم هو نصف قطر مدار الأرض، وتبلغ السرعة الأولية 30 كم/ثانية، والسرعة النهائية تساوي صفرًا، لذا يمكننا حل المسافة عند هذه النقطة من معادلة حفظ الطاقة. باستخدام R _ES = 1.50 × 10 ¹¹ م و M _Sun = 1.99 × 10 ³⁰ كجم، لدينا

\[\begin{split} \frac{1}{2} mv_{1}^{2} - \frac{GMm}{r_{1}} & = \frac{1}{2} mv_{2}^{2} - \frac{GMm}{r_{2}} \\ \frac{1}{2} \cancel{m} (30\; km/s)^{2} - \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(1.99 \times 10^{30}\; kg) \cancel{m}}{1.50 \times 10^{11}\; m} & = \frac{1}{2} m(0)^{2} - \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(1.99 \times 10^{30}\; kg) \cancel{m}}{r_{2}} \end{split}\]

حيث يتم إلغاء الكتلة m. عند حل r ₂ نحصل على r ₂ = 3.0 × 10 ¹¹ م، لاحظ أن هذه هي ضعف المسافة الأولية من الشمس وتأخذنا عبر مدار المريخ، ولكن ليس تمامًا إلى حزام الكويكبات.

الأهمية

وصل الكائن في هذه الحالة إلى مسافة ضعف المسافة المدارية الأولية بالضبط. سنرى سبب ذلك في القسم التالي عندما نحسب سرعة المدارات الدائرية.

التمارين الرياضية\(\PageIndex{3}\)

افترض أنك في مركبة فضائية في مدار حول الشمس في مدار الأرض، ولكن بعيدًا عن الأرض (بحيث يمكن تجاهلها). كيف يمكنك إعادة توجيه سرعتك العرضية إلى الاتجاه الشعاعي بحيث يمكنك بعد ذلك المرور عبر مدار المريخ؟ ما المطلوب لتغيير اتجاه السرعة فقط؟