13.3: الجاذبية بالقرب من سطح الأرض
- Page ID
- 199932
- اشرح العلاقة بين الثوابت G و g
- أوجد كتلة جسم فلكي من خلال تسارع السقوط الحر على سطحه
- وصف كيفية اختلاف قيمة g بسبب الموقع ودوران الأرض
في هذا القسم، نلاحظ كيفية تطبيق قانون نيوتن للجاذبية على سطح الكوكب وكيفية ارتباطه بما تعلمناه سابقًا عن السقوط الحر. ندرس أيضًا تأثيرات الجاذبية داخل الأجسام الكروية.
الوزن
تذكر أن تسارع جسم يسقط بحرية بالقرب من سطح الأرض يبلغ تقريبًا g = 9.80 m/s 2. القوة المسببة لهذا التسارع تسمى وزن الجسم، ومن قانون نيوتن الثاني، له القيمة mg. هذا الوزن موجود بغض النظر عما إذا كان الكائن في حالة سقوط حر. نحن نعلم الآن أن هذه القوة هي قوة الجاذبية بين الجسم والأرض. إذا استبدلنا mg بحجم m\(\vec{F}_{12}\) في قانون نيوتن للجذب العام، و m بـ m 1، و M E عن m 2، نحصل على المعادلة العددية
\[mg = G \frac{m M_{E}}{r^{2}} \label{13.1}\]
حيث r هي المسافة بين مراكز كتلة الجسم والأرض. يبلغ متوسط نصف قطر الأرض حوالي 6370 كم. وبالتالي، بالنسبة للأجسام التي تقع على بعد بضعة كيلومترات من سطح الأرض، يمكننا أن نأخذ\(r = R_E\) (الشكل\(\PageIndex{1}\)). يتم إلغاء الكتلة m من الكائن، تاركًا
\[g = G \frac{M_{E}}{r^{2}} \ldotp \label{13.2}\]
وهذا يفسر سبب سقوط جميع الجماهير بحرية بنفس التسارع. لقد تجاهلنا حقيقة أن الأرض تتسارع أيضًا نحو الجسم الساقط، ولكن هذا مقبول طالما أن كتلة الأرض أكبر بكثير من كتلة الجسم.
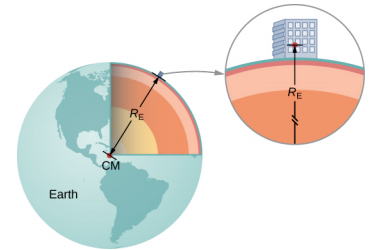
هل تساءلت يومًا كيف نعرف كتلة الأرض؟ بالتأكيد لا يمكننا وضعها على مقياس. تم قياس قيم g ونصف قطر الأرض بدقة معقولة منذ قرون.
- استخدم القيم القياسية لـ g وR E والمعادلة\ ref {13.2} لإيجاد كتلة الأرض.
- قدِّر قيمة g على القمر. استخدم حقيقة أن نصف قطر القمر يبلغ حوالي 1700 كم (تم تحديد قيمة هذه الدقة منذ عدة قرون) وافترض أنه له نفس متوسط كثافة الأرض، 5500 كجم/م 3.
إستراتيجية
باستخدام القيم المعروفة لـ g و R E، يمكننا استخدام المعادلة\ ref {13.2} للعثور على M E. بالنسبة للقمر، نستخدم افتراض متوسط الكثافة المتساوي لتحديد الكتلة من نسبة أحجام الأرض والقمر.
الحل
- عند إعادة ترتيب المعادلة\ المرجع {13.2}، لدينا $M_ {E} =\ frac {g R_ {E} ^ {2} {G} =\ frac {(9.80\؛ م/s^ {2}) (6.37\ مرات 10^ {6}\\\؛ {2}} {6.67\ مرات 10^ {-11}\؛ {\ cdotp m^ 2} /كجم^ {2}} = 5.95\ مرات 10 ^ {24}\؛ كجم\ ldotp $$
- يتناسب حجم الكرة مع نصف القطر المكعب، لذا فإن النسبة البسيطة تعطينا $$\ frac {M_ {M}} {M_ {E}} =\ frac {R_ {M} ^ {3}} {R_ {E} ^ {3}}\ السهم الأيمن M_ {M} =\ يسار (\ dfrac {(1.7\ مرات 10 ^ {6}\ م) ^ {3}} {(6.37\ مرات 10 ^ {6}\؛ م) ^ {3}}\ يمين) (5.95\ مرات 10 ^ {24}\؛ كجم) = 1.1\ مرات 10 ^ {23}\؛ كجم\ lDotP$$نحن نستخدم الآن المعادلة\ المرجع {13.2}. $g_ {M} = G\ frac {M_ {M} {r_ {M} ^ {2}} = (6.67\ مرات 10^ {-11}\؛ N\؛\ cdotp m^ {2} /كج ^ {2})\ يسار (\ دفراك {1.1\ مرات 10^ {1\ مرات 10\\\ م)؛) ^ {2}}\ يمين) = 2.5\؛ م/ثانية^ {2} $$
الأهمية
بمجرد أن حدد كافنديش قيمة G في عام 1798، يمكن حساب كتلة الأرض. (في الواقع، كان هذا هو الغرض النهائي من تجربة كافنديش في المقام الأول.) القيمة التي قمنا بحسابها لـ g من القمر غير صحيحة. يبلغ متوسط كثافة القمر في الواقع 3340 كجم/م 3 فقط و g = 1.6 m/s 2 على السطح. حاول نيوتن قياس كتلة القمر من خلال مقارنة تأثير الشمس على المد والجزر في محيط الأرض مقارنة بتأثير القمر. كانت قيمته عاملًا صغيرًا جدًا. تأتي القيم الأكثر دقة لـ g وكتلة القمر من تتبع حركة المركبات الفضائية التي تدور حول القمر. ولكن يمكن تحديد كتلة القمر بدقة دون الذهاب إلى القمر. تدور الأرض والقمر حول مركز مشترك للكتلة، ويمكن للقياسات الفلكية الدقيقة تحديد هذا الموقع. نسبة كتلة القمر إلى كتلة الأرض هي نسبة [المسافة من مركز الكتلة المشترك إلى مركز القمر] إلى [المسافة من مركز الكتلة المشترك إلى مركز الأرض].
لاحقًا في هذا القسم، سنرى أن كتلة الأجسام الفلكية الأخرى يمكن تحديدها أيضًا من خلال فترة الأقمار الصناعية الصغيرة التي تدور حولها. ولكن حتى حدد كافنديش قيمة G، كانت كتل كل هذه الأجسام غير معروفة.
ما قيمة g 400 km فوق سطح الأرض، حيث توجد محطة الفضاء الدولية في المدار؟
الحل
باستخدام قيمة M E وملاحظة أن نصف القطر هو r = R E + 400 كم، نستخدم المعادلة\ ref {13.2} للعثور على g. من المعادلة\ المرجع {13.2} لدينا
\[g = G \frac{M_{E}}{r^{2}} = (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2}) \left(\dfrac{5.96 \times 10^{24}\; kg}{(6.37 \times 10^{6} + 400 \times 10^{3}\; m)^{2}}\right) = 8.67\; m/s^{2} \ldotp\]
الأهمية
غالبًا ما نشاهد مقطع فيديو لرواد الفضاء في محطات الفضاء، ويبدو أنهم يفتقرون إلى الوزن. لكن من الواضح أن قوة الجاذبية تعمل عليها. بمقارنة قيمة g التي قمنا بحسابها للتو مع تلك الموجودة على الأرض (9.80 م/ث 2)، نرى أن رواد الفضاء في محطة الفضاء الدولية لا يزالون يمتلكون 88٪ من وزنهم. يبدو أنها عديمة الوزن فقط لأنها في حالة سقوط حر. سنعود إلى هذا في مدارات الأقمار الصناعية والطاقة.
كيف يقارن وزنك في الجزء العلوي من مبنى طويل بوزنك في الطابق الأول؟ هل تعتقد أن المهندسين بحاجة إلى مراعاة التغيير في قيمة g عند تصميم الدعم الهيكلي لمبنى طويل جدًا؟
مجال الجاذبية
المعادلة\ ref {13.2} هي معادلة عددية تعطي مقدار تسارع الجاذبية كدالة للمسافة من مركز الكتلة التي تسبب التسارع. ولكن كان بإمكاننا الاحتفاظ بالشكل المتجه لقوة الجاذبية في المعادلة\ ref {13.1}، وكتابة التسارع في شكل متجه كـ
\[\vec{g} = G \frac{M}{r^{2}} \hat{r} \ldotp\]
نحدد مجال المتجهات الذي\(\vec{g}\) يمثله مجال الجاذبية الناتج عن الكتلة M. يمكننا تصوير الحقل كما هو موضح في الشكل\(\PageIndex{2}\). يتم توجيه الخطوط شعاعيًا إلى الداخل ويتم توزيعها بشكل متماثل حول الكتلة.
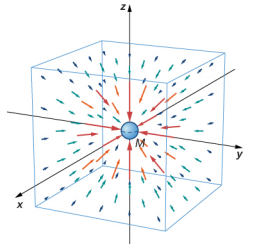
كما هو الحال بالنسبة لأي حقل متجه،\(\vec{g}\) يكون الاتجاه موازيًا لخطوط الحقل في أي نقطة. تتناسب قوة أي\(\vec{g}\) نقطة عكسياً مع تباعد الأسطر. هناك طريقة أخرى لتوضيح ذلك وهي أن حجم المجال في أي منطقة يتناسب مع عدد الخطوط التي تمر عبر مساحة سطح الوحدة، وهي كثافة الخطوط بشكل فعال. نظرًا لأن الخطوط متباعدة بالتساوي في جميع الاتجاهات، فإن عدد الخطوط لكل وحدة مساحة على مسافة r من الكتلة هو إجمالي عدد الخطوط مقسومًا على مساحة سطح كرة نصف قطرها r، والتي تتناسب مع r 2. ومن ثم، فإن هذه الصورة تمثل تمامًا قانون المربع العكسي، بالإضافة إلى الإشارة إلى اتجاه الحقل. في الصورة الميدانية، نقول أن الكتلة m تتفاعل مع مجال الجاذبية للكتلة M. سنستخدم مفهوم الحقول لتحقيق ميزة كبيرة في الأقسام اللاحقة حول الكهرومغناطيسية.
الوزن الظاهري: حساب دوران الأرض
كما رأينا في تطبيقات قوانين نيوتن، فإن الأجسام التي تتحرك بسرعة ثابتة في دائرة لها عجلة جاذبية مركزية موجهة نحو مركز الدائرة، مما يعني أنه يجب أن تكون هناك قوة صافية موجهة نحو مركز تلك الدائرة. نظرًا لأن جميع الأجسام الموجودة على سطح الأرض تتحرك عبر دائرة كل 24 ساعة، يجب أن تكون هناك قوة جذب صافية على كل جسم موجه نحو مركز تلك الدائرة.
لننظر أولاً في كائن كتلته m يقع عند خط الاستواء، معلقًا من مقياس (الشكل\(\PageIndex{3}\)). يُحدث المقياس قوة تصاعدية\(\vec{F}_{s}\) بعيدًا عن مركز الأرض. هذه هي القراءة على المقياس، وبالتالي فهي الوزن الظاهري للكائن. يشير الوزن (mg) نحو مركز الأرض. إذا لم تكن الأرض تدور، فسيكون التسارع صفرًا، وبالتالي ستكون القوة الصافية صفرًا، مما ينتج عنه F s = mg. ستكون هذه القراءة الحقيقية للوزن.
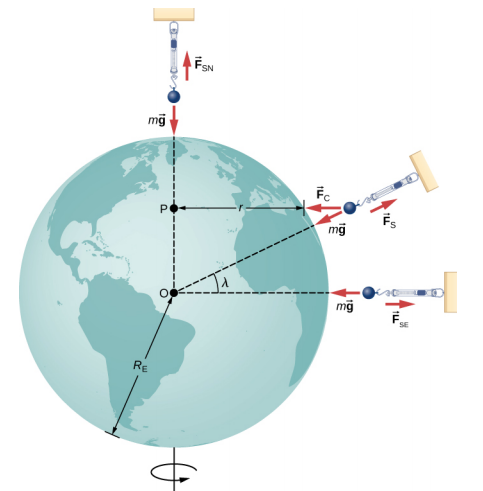
مع الدوران، يجب أن يوفر مجموع هذه القوى التسارع المركزي\(a_c\). باستخدام قانون نيوتن الثاني، لدينا
\[\sum F = F_{s} - mg = ma_{c} \quad where\; a_{c} = - \frac{v^{2}}{r} \ldotp \label{13.3}\]
لاحظ أن a c تشير في نفس اتجاه الوزن؛ وبالتالي فهي سلبية. السرعة العرضية v هي السرعة عند خط الاستواء و r هي R E. يمكننا حساب السرعة ببساطة من خلال ملاحظة أن الأجسام الموجودة على خط الاستواء تسافر في محيط الأرض خلال 24 ساعة. بدلاً من ذلك، دعونا نستخدم التعبير البديل لـ c من الحركة في بعدين وثلاثة أبعاد. تذكر أن السرعة العرضية مرتبطة بالسرعة الزاوية (\(\omega\)) بواسطة v = r\(\omega\). وبالتالي، لدينا c = −r\(\omega\) 2. من خلال إعادة ترتيب المعادلة 13.3 واستبدال r = R E، يكون الوزن الظاهري عند خط الاستواء
\[F_{s} = m (g - R_{E} \omega^{2}) \ldotp\]
السرعة الزاوية للأرض في كل مكان هي
\[\omega = \frac{2 \pi\; rad}{24\; hr \times 3600\; s/hr} = 7.27 \times 10^{-5}\; rad/s \ldotp\]
باستبدال قيم R E و\(\omega\)، لدينا R E\(\omega\) 2 = 0.0337 م/ث 2. هذا يمثل 0.34٪ فقط من قيمة الجاذبية، لذلك من الواضح أنه تصحيح صغير.
ما السرعة التي تحتاجها الأرض للدوران حتى لا يكون لدى أولئك الموجودين عند خط الاستواء أي وزن واضح؟ كم سيكون طول اليوم؟
إستراتيجية
باستخدام المعادلة\ ref {13.3}، يمكننا ضبط الوزن الظاهري (F s) على الصفر وتحديد التسارع المركزي المطلوب. من ذلك، يمكننا أن نجد السرعة عند خط الاستواء. طول اليوم هو الوقت المطلوب لدورة واحدة كاملة.
الحل
من المعادلة\ المرجع {13.2}، لدينا\(\sum\) F = F s − mg = ma c، لذا عند ضبط F s = 0، نحصل على g = a c. باستخدام تعبير c، ليحل محل نصف قطر الأرض والقيمة القياسية للجاذبية، نحصل على
\[\begin{split} a_{c} & = \frac{v^{2}}{r} = g \\ v & = \sqrt{gr} = \sqrt{(9.80\; m/s^{2})(6.37 \times 10^{6}\; m)} = 7.91 \times 10^{3}\; m/s \ldotp \end{split}\]
الفترة T هي الوقت المناسب لدورة واحدة كاملة. لذلك، السرعة العرضية هي المحيط مقسومًا على T، لذلك لدينا
\[\begin{split} v & = \frac{2 \pi r}{T} \\ T & = \frac{2 \pi r}{v} = \frac{2 \pi (6.37 \times 10^{6}\; m)}{7.91 \times 10^{3}\; m/s} = 5.06 \times 10^{3}\; s \ldotp \end{split}\]
هذا حوالي 84 دقيقة.
الأهمية
سنرى لاحقًا في هذا القسم أن هذه السرعة وطول اليوم سيكونان أيضًا السرعة المدارية وفترة القمر الصناعي في المدار على سطح الأرض. في حين أن مثل هذا المدار لن يكون ممكنًا بالقرب من سطح الأرض بسبب مقاومة الهواء، فمن المؤكد أنه ممكن فقط على بعد بضع مئات من الأميال فوق الأرض.
نتائج بعيدة عن خط الاستواء
في القطبين، a c → 0 و Fs = mg، تمامًا كما هو الحال بدون دوران. في أي خط عرض آخر\(\lambda\)، يكون الوضع أكثر تعقيدًا. يتم توجيه التسارع المركزي نحو النقطة P في الشكل، ويصبح نصف القطر\(r = R_E \cos \lambda\). يجب أن يشير المجموع المتجه للوزن\(\vec{F}_{s}\) ويجب أن يشير إلى النقطة P، وبالتالي لم\(\vec{F}_{s}\) يعد يشير بعيدًا عن مركز الأرض. (الفرق صغير ومبالغ فيه في الشكل.) سيشير البومب بوب دائمًا على طول هذا الاتجاه المنحرف. تم بناء جميع المباني بمحاذاة هذا الاتجاه المنحرف، وليس على طول دائرة نصف قطرها عبر مركز الأرض. بالنسبة للمباني الأطول، يمثل هذا انحرافًا لبضعة أقدام في الأعلى.
من الجدير بالذكر أيضًا أن الأرض ليست كرة مثالية. الجزء الداخلي سائل جزئيًا، وهذا يعزز انتفاخ الأرض عند خط الاستواء بسبب دورانها. يبلغ نصف قطر الأرض حوالي 30 كم عند خط الاستواء مقارنة بالقطبين. يُترك كتمرين لمقارنة قوة الجاذبية عند القطبين بتلك الموجودة عند خط الاستواء باستخدام المعادلة\ ref {13.2}. الفرق قابل للمقارنة مع الفرق بسبب الدوران وهو في نفس الاتجاه. يبدو أنه يمكنك حقًا فقدان «الوزن» بالانتقال إلى المناطق الاستوائية.
الجاذبية بعيدًا عن السطح
ذكرنا سابقًا دون دليل أن قانون الجاذبية ينطبق على الأجسام المتماثلة كرويًا، حيث تعمل كتلة كل جسم كما لو كانت في مركز الجسم. نظرًا لأن المعادلة\ ref {13.2} مشتقة من المعادلة\ ref {13.1}، فهي صالحة أيضًا لتوزيعات الكتلة المتماثلة، ولكن كلتا المعادلتين صالحتان فقط لقيم\(r ≥ R_E\). كما رأينا في المثال 13.4، على ارتفاع 400 كم فوق سطح الأرض، حيث تدور محطة الفضاء الدولية،\(g\) تبلغ القيمة 8.67 م/ث 2. (سنرى لاحقًا أن هذا هو أيضًا التسارع المركزي لمحطة الفضاء الدولية.)
بالنسبة إلى\(r < R_E\) المعادلة\ المرجع {13.1} والمعادلة\ المرجع {13.2} غير صالحين. ومع ذلك، يمكننا تحديد g لهذه الحالات باستخدام مبدأ يأتي من قانون Gauss، وهو أداة رياضية قوية ندرسها بمزيد من التفصيل لاحقًا في الدورة. نتيجة قانون غاوس، المطبق على الجاذبية، هي أن الكتلة داخل r فقط هي التي تساهم في قوة الجاذبية. كما يمكن اعتبار هذه الكتلة، تمامًا كما كانت من قبل، موجودة في المركز. تأثير الجاذبية للكتلة خارج r له تأثير صافي صفري.
تحدث حالتان خاصتان مثيرتان للغاية. بالنسبة للكوكب الكروي ذي الكثافة الثابتة، فإن الكتلة داخل r هي الكثافة مضروبة في الحجم داخل r، ويمكن اعتبار هذه الكتلة موجودة في المركز. استبدال M E بالكتلة داخل r فقط، M =\(\rho\) x (حجم الكرة)، و R E بـ r، تصبح المعادلة\ المرجع {13.2}
\[g = G \frac{M_{E}}{R_{E}^{2}} = G \frac{\rho \left(\dfrac{4}{3} \pi r^{3}\right)}{r^{2}} = \frac{4}{3} G \rho \pi r \ldotp\]
تنخفض قيمة g، وبالتالي وزنك، خطيًا عندما تنزل إلى أسفل حفرة إلى مركز الكوكب الكروي. في الوسط، أنت عديم الوزن، حيث تسحب كتلة الكوكب بالتساوي في جميع الاتجاهات. في الواقع، كثافة الأرض ليست ثابتة، ولا الأرض صلبة في جميع الأنحاء. \(\PageIndex{4}\)يوضح الشكل صورة ما\(g\) إذا كانت الأرض ذات كثافة ثابتة والملف الشخصي الأكثر احتمالاً بناءً على تقديرات الكثافة المشتقة من البيانات الزلزالية.
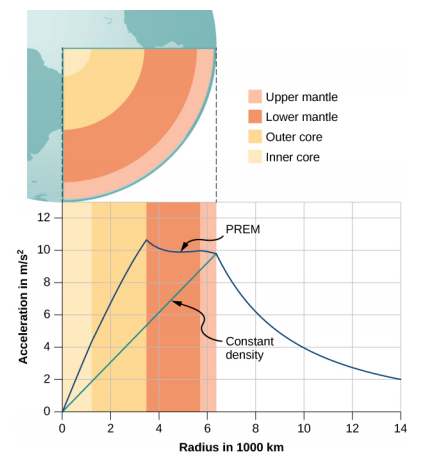
الحالة الثانية المثيرة للاهتمام تتعلق بالعيش على كوكب ذو قشرة كروية. تم اقتراح هذا السيناريو في العديد من قصص الخيال العلمي. وفي تجاهل المشكلات الهندسية الهامة، يمكن بناء الغلاف بنصف القطر المطلوب والكتلة الكلية، بحيث يكون g على السطح هو نفس كتلة الأرض. هل يمكنك تخمين ما يحدث بمجرد نزولك في المصعد إلى داخل الغلاف، حيث لا توجد كتلة بينك وبين المركز؟ ما الفوائد التي يوفرها ذلك للسفر لمسافات كبيرة من نقطة على الكرة إلى أخرى؟ وأخيرًا، ما هو التأثير الذي سيحدث إذا كان الكوكب يدور؟


