13.2: قانون نيوتن للجذب العام
- Page ID
- 199933
- ضع قائمة بالمعالم المهمة في تاريخ الجاذبية
- احسب قوة الجاذبية بين كتلتين
- تقدير قوة الجاذبية بين مجموعات الكتلة
نستعرض أولاً تاريخ دراسة الجاذبية، مع التركيز على تلك الظواهر التي ألهمت الفلاسفة والعلماء لآلاف السنين للبحث عن تفسير. ثم ندرس أبسط شكل من أشكال قانون نيوتن للجاذبية العامة وكيفية تطبيقه.
تاريخ الجاذبية
تساءل الفلاسفة الأوائل لماذا تميل الأشياء بشكل طبيعي إلى السقوط نحو الأرض. اعتقد أرسطو (384-322 قبل الميلاد) أن طبيعة الصخور هي البحث عن الأرض وطبيعة النار للبحث عن السماوات. افترض براهماجوبتا (598 ~ 665 م) أن الأرض عبارة عن كرة وأن الأجسام تمتلك تقاربًا طبيعيًا لها، حيث سقطت باتجاه المركز من أي مكان تقع فيه.
تمت دراسة حركات الشمس وقمرنا والكواكب لآلاف السنين أيضًا. وقد وصف بطليموس (90—168 م) هذه الحركات بدقة مذهلة، حيث وصف أسلوبه في الدراجات مسارات الكواكب كدوائر داخل دوائر. ومع ذلك، هناك القليل من الأدلة على أن أي شخص ربط حركة الأجسام الفلكية بحركة الأجسام الساقطة على الأرض - حتى القرن السابع عشر.
يُنسب عمومًا إلى نيكولاوس كوبرنيكوس (1473—1543) أنه أول من تحدى نظام بطليموس المركزي (المتمركز حول الأرض) واقترح نظامًا مركزيًا للشمس، حيث تكون الشمس في مركز النظام الشمسي. تم دعم هذه الفكرة من خلال القياسات الدقيقة بالعين المجردة لحركات الكواكب بواسطة Tycho Brahe وتحليلها من قبل يوهانس كيبلر وغاليليو غاليلي. أظهر كيبلر أن حركة كل كوكب عبارة عن شكل بيضاوي (أول قوانينه الثلاثة، التي تمت مناقشتها في قوانين كيبلر لحركة الكواكب)، واقترح روبرت هوك (نفس هوك الذي صاغ قانون هوك للينابيع) بشكل بديهي أن هذه الحركات ترجع إلى جذب الكواكب إلى شمس. ومع ذلك، كان إسحاق نيوتن هو الذي ربط تسارع الأجسام بالقرب من سطح الأرض بالتسارع المركزي للقمر في مداره حول الأرض.
أخيرًا، في نظرية الجاذبية لأينشتاين، ننظر إلى نظرية النسبية العامة التي اقترحها ألبرت أينشتاين في عام 1916. تأتي نظريته من منظور مختلف تمامًا، حيث تكون الجاذبية مظهرًا من مظاهر التشوه الجماعي للفضاء والزمان. أدت عواقب نظريته إلى ظهور العديد من التنبؤات الرائعة، والتي تم تأكيدها جميعًا بشكل أساسي على مدى العقود العديدة التي أعقبت نشر النظرية (بما في ذلك قياس موجات الجاذبية لعام 2015 من اندماج ثقبين أسودين).
قانون نيوتن للجذب العام
لاحظ نيوتن أن الأجسام الموجودة على سطح الأرض (وبالتالي على مسافة R E من مركز الأرض) تتسارع بمقدار g، لكن القمر، على مسافة حوالي 60 R E، له تسارع مركزي بحوالي (60) مرتين أصغر من g، ويمكنه تفسير ذلك من خلال الافتراض وجود قوة بين أي جسمين، يُقاس حجمهما بحاصل ضرب الكتلتين مقسومًا على مربع المسافة بينهما. نحن نعلم الآن أن قانون التربيع العكسي هذا موجود في كل مكان بطبيعته، وهو دالة هندسية لمصادر النقاط. تنتشر قوة أي مصدر على مسافة r على سطح كرة تتمحور حول الكتلة. تتناسب مساحة سطح تلك الكرة مع r 2. في الفصول اللاحقة، نرى نفس الشكل في القوة الكهرومغناطيسية.
يمكن التعبير عن قانون نيوتن للجاذبية كـ
\[\vec{F}_{12} = G \frac{m_{1} m_{2}}{r^{2}} \hat{r}_{12} \label{13.1}\]
\(\vec{F}_{12}\)أين القوة المؤثرة على الجسم 1 التي يمارسها الكائن 2\(\hat{r}_{12}\) وهو متجه الوحدة الذي يشير من الكائن 1 نحو الكائن 2.
كما هو موضح في الشكل\(\PageIndex{1}\)، يشير\(\vec{F}_{12}\) المتجه من الكائن 1 نحو الكائن 2، وبالتالي يمثل قوة جذابة بين الكائنات. القوة المتساوية ولكن المعاكسة\(\vec{F}_{21}\) هي القوة المؤثِّرة على الجسم 2 بفعل الجسم 1.
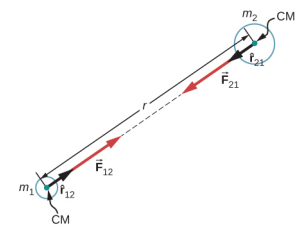
تعكس هذه القوى المتساوية ولكن المعاكسة قانون نيوتن الثالث، الذي ناقشناه سابقًا. لاحظ أنه بالمعنى الدقيق للكلمة، تنطبق المعادلة\ ref {13.1} على الكتل النقطية - كل الكتلة تقع في نقطة واحدة. ولكنه ينطبق بالتساوي على أي أجسام متماثلة كرويًا، حيث r هي المسافة بين مراكز كتلة تلك الأجسام. في كثير من الحالات، يعمل بشكل جيد بشكل معقول مع الأجسام غير المتماثلة، إذا كان فصلها كبيرًا مقارنة بحجمها، ونأخذ r لتكون المسافة بين مركز كتلة كل جسم.
تجربة كافنديش
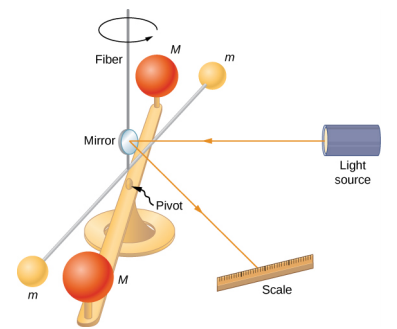
بعد قرن من نشر نيوتن لقانون الجاذبية العالمية، حدد هنري كافنديش ثابت التناسب G من خلال إجراء تجربة مضنية. قام ببناء جهاز مشابه للجهاز الموضح في الشكل\(\PageIndex{2}\)، حيث يتم تعليق الكتل الصغيرة من السلك. بمجرد الوصول إلى حالة الاتزان، يتم وضع كتلتين ثابتتين أكبر حجمًا بشكل متماثل بالقرب من الكتل الأصغر. تؤدي جاذبية الجاذبية إلى حدوث التواء (التواء) في السلك الداعم الذي يمكن قياسه.
يُطلق على الثابت G اسم ثابت الجاذبية الشامل، وقد حدده كافنديش على أنه G = 6.67 × 10 −11 N • m 2/kg 2. تشير كلمة «عالمي» إلى أن العلماء يعتقدون أن هذا الثابت ينطبق على الكتل من أي تركيبة وأنه هو نفسه في جميع أنحاء الكون. قيمة G هي رقم صغير للغاية، مما يدل على أن قوة الجاذبية ضعيفة جدًا. إن الجاذبية بين الكتل الصغيرة مثل أجسادنا، أو حتى الأجسام بحجم ناطحات السحاب، صغيرة للغاية. على سبيل المثال، تؤثر كتلتان كلتاهما بوزن 1.0 كجم على بعضهما البعض قوة مقدارها 6.7 × 10 −11 نيوتن على بعضهما البعض. هذا هو وزن حبة حبوب اللقاح النموذجية.
على الرغم من أن الجاذبية هي أضعف القوى الأساسية الأربعة للطبيعة، إلا أن طبيعتها الجذابة هي التي تحملنا على الأرض، وتجعل الكواكب تدور حول الشمس والشمس لتدور حول مجرتنا، وتربط المجرات في مجموعات تتراوح من بضعة إلى ملايين. الجاذبية هي القوة التي تشكل الكون.
لتحديد الحركة الناتجة عن قوة الجاذبية، اتبع الخطوات التالية:
- حدِّد الكتلتين، واحدة أو كلتاهما، التي ترغب في إيجاد قوة الجاذبية لها.
- ارسم مخططًا للجسم الحر، مع رسم القوة المؤثرة على كل كتلة والإشارة إلى المسافة بين مراكز كتلتها.
- طبّق قانون نيوتن الثاني للحركة على كل كتلة لتحديد كيفية تحركها.
ولنأخذ بعين الاعتبار مركبتين من طراز سويوز شبه كروية، في مدار حول الأرض، وكتلة كل منهما 9000 كجم وقطرها 4.0 أمتار، وهما في البداية في حالة سكون بالنسبة لبعضهما البعض، على بعد 10.0 متر من المركز إلى المركز. (كما سنرى في قوانين كيبلر لحركة الكواكب، يدور كلاهما حول الأرض بنفس السرعة ويتفاعلان تقريبًا كما لو كانا معزولين في الفضاء السحيق.) أوجد قوة الجاذبية بينهما وبين التسارع الأولي. قدِّر المدة التي يستغرقها الانجراف معًا، ومدى سرعة تحركهما عند الارتطام.
إستراتيجية
نستخدم قانون نيوتن للجاذبية لتحديد القوة بينهما ثم نستخدم قانون نيوتن الثاني لإيجاد عجلة كل منهما. وللتقدير، نفترض أن هذا التسارع ثابت، ونستخدم معادلات التسارع الثابت من الحركة على طول الخط المستقيم لإيجاد وقت التصادم وسرعته.
الحل
حجم القوة هو
\[|\vec{F}_{12}| = F_{12} = G \frac{m_{1} m_{2}}{r^{2}} = (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2}) \frac{(9000\; kg)(9000\; kg)}{(10\; m)^{2}} = 5.4 \times 10^{-5}\; N \ldotp\]
التسارع الأولي لكل حمولة هو
\[a = \frac{F}{m} = \frac{5.4 \times 10^{-5}\; N}{9000\; kg} = 6.0 \times 10^{-9}\; m/s^{2} \ldotp\]
يبلغ قطر المركبات 4.0 أمتار، وبالتالي تتحرك المركبات من 10.0 متر إلى 4.0 متر عن بعضها البعض، أو مسافة 3.0 متر لكل منها. طريقة حسابية مماثلة لما ورد أعلاه، فعندما تكون المركبات على مسافة 4.0 أمتار، ينتج تسارع قدره 3.8 × 10 −8 م/ث 2، ومتوسط هاتين القيمتين هو 2.2 × 10 −8 م/ث 2. إذا افترضنا تسارعًا ثابتًا لهذه القيمة وبدأت من السكون، فإن المركبات تصطدم بالسرعة المعطاة بواسطة
\[v^{2} = v_{0}^{2} + 2a (x - x_{0}),\; where\; v_{0} = 0,\]
وبالتالي
\[v = \sqrt{2(2.2 \times 10^{-9}\; N)(3.0\; m)} = 3.6 \times 10^{-4}\; m/s \ldotp\]
نستخدم v = v 0 + at للعثور على t = v/a = 1.7 × 10 4 ثانية أو حوالي 4.6 ساعة.
الدلالة
هذه الحسابات - بما في ذلك القوة الأولية - هي مجرد تقديرات، حيث ربما لا تكون المركبات متماثلة كرويًا. ولكن يمكنك أن ترى أن القوة صغيرة بشكل لا يصدق. يجب على رواد الفضاء ربط أنفسهم عند القيام بالعمل خارج حتى محطة الفضاء الدولية الضخمة (ISS)، كما هو موضح في الشكل\(\PageIndex{3}\)، لأن الجاذبية لا يمكن أن تنقذهم حتى من أصغر دفعة بعيدًا عن المحطة.

ماذا يحدث للقوة والتسارع عندما تسقط المركبات معًا؟ ما تقديراتنا للسرعة عند تصادم أعلى أو أقل من السرعة الفعلية؟ وأخيرًا، ماذا سيحدث إذا لم تكن الجماهير متطابقة؟ هل ستكون القوة على كل منها هي نفسها أم مختلفة؟ ماذا عن تسريعاتها؟
- إجابة
-
أضف نصوصًا هنا. لا تحذف هذا النص أولاً.
إن تأثير الجاذبية بين جسمين لهما كتل على ترتيب هذه المركبات الفضائية صغير بالفعل. ومع ذلك، فإن تأثير الجاذبية عليك من الأرض مهم بما يكفي لأن السقوط في الأرض لمسافة بضعة أقدام فقط يمكن أن يكون خطيرًا. ندرس قوة الجاذبية بالقرب من سطح الأرض في القسم التالي.
أوجد تسارع مجرتنا، درب التبانة، بسبب أقرب مجرة ذات حجم مماثل، مجرة أندروميدا (الشكل\(\PageIndex{4}\)). تبلغ الكتلة التقريبية لكل مجرة 800 مليار كتلة شمسية (الكتلة الشمسية هي كتلة شمسنا)، ويتم فصلها بـ 2.5 مليون سنة ضوئية. (لاحظ أن كتلة أندروميدا ليست معروفة جيدًا ولكن يُعتقد أنها أكبر قليلاً من مجرتنا.) يبلغ قطر كل مجرة حوالي 100000 سنة ضوئية (سنة ضوئية واحدة = 9.5 × 10 15 م).

إستراتيجية
كما في المثال السابق، نستخدم قانون نيوتن للجاذبية لتحديد القوة بينهما ثم نستخدم قانون نيوتن الثاني لإيجاد تسارع درب التبانة. يمكننا اعتبار المجرات كتلًا نقطية، نظرًا لأن أحجامها أصغر بحوالي 25 مرة من انفصالها. تبلغ كتلة الشمس (انظر الملحق D) 2.0 × 10 30 كجم والسنة الضوئية هي المسافة التي يقطعها الضوء في عام واحد، 9.5 × 10 15 م.
الحل
حجم القوة هو
\[F_{12} = G \frac{m_{1} m_{2}}{r^{2}} = (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2}) \frac{[(800 \times 10^{9})(2.0 \times 10^{30}\; kg)]^{2}}{[(2.5 \times 10^{6})(9.5 \times 10^{15}\; m)]^{2}} = 3.0 \times 10^{29}\; N \ldotp\]
تسارع درب التبانة هو
\[a = \frac{F}{m} = \frac{3.0 \times 10^{29}\; N}{(800 \times 10^{9})(2.0 \times 10^{30}\; kg)} = 1.9 \times 10^{-13}\; m/s^{2} \ldotp\]
الدلالة
هل تبدو قيمة التسارع هذه صغيرة بشكل مذهل؟ إذا بدأوا من الراحة، فسوف يتسارعون مباشرة نحو بعضهم البعض، «ويصطدمون» في مركز كتلتهم. دعونا نقدر وقت حدوث ذلك. التسارع الأولي هو ~10 −13 م/ث 2، لذلك باستخدام v = at، نرى أن الأمر سيستغرق حوالي 10 13 ثانية حتى تصل كل مجرة إلى سرعة 1.0 متر/ثانية، وستكون أقرب بمقدار ~0.5 × 10 13 مترًا فقط. وهذا أصغر بتسعة مراتب من المسافة الأولية بينهما. في الواقع، نادرًا ما تكون مثل هذه الحركات بسيطة. ترتبط هاتان المجرتان، إلى جانب حوالي 50 مجرة أخرى أصغر حجمًا، بالجاذبية في مجموعتنا المحلية. ترتبط مجموعتنا المحلية بالجاذبية بمجموعات أخرى في ما يسمى بالكتلة الفائقة. كل هذا جزء من الرقصة الكونية العظيمة الناتجة عن الجاذبية، كما هو موضح في الشكل\(\PageIndex{5}\).