12.3: أمثلة على الاتزان الثابت

أهداف التعلم

• تحديد وتحليل حالات التوازن الثابت
• قم بإعداد مخطط الجسم الحر لكائن ممتد في حالة توازن ثابت
• إعداد وحل ظروف التوازن الثابت للكائنات في حالة توازن في حالات فيزيائية مختلفة

جميع الأمثلة في هذا الفصل هي مشاكل مستوية. وفقًا لذلك، نستخدم شروط التوازن في الشكل المكون للمعادلة 12.2.9 إلى المعادلة 12.2.11. قدمنا إستراتيجية حل المشكلات في المثال 12.1 لتوضيح المعنى المادي لظروف التوازن. الآن نقوم بتعميم هذه الإستراتيجية في قائمة الخطوات التي يجب اتباعها عند حل مشاكل التوازن الثابت للأجسام الصلبة الممتدة. نمضي في خمس خطوات عملية.

إستراتيجية حل المشكلات: الاتزان الثابت

1. حدد الكائن الذي سيتم تحليله. بالنسبة لبعض الأنظمة في حالة التوازن، قد يكون من الضروري النظر في أكثر من كائن واحد. حدد جميع القوى المؤثرة على الكائن. حدد الأسئلة التي تحتاج إلى الإجابة عليها. حدد المعلومات الواردة في المشكلة. في المشكلات الواقعية، قد تكون بعض المعلومات الأساسية مضمنة في الموقف بدلاً من تقديمها بشكل صريح.
2. قم بإعداد مخطط الجسم الحر للكائن. (أ) اختر الإطار المرجعي x للمشكلة. ارسم مخططًا للجسم الحر للكائن، بما في ذلك القوى التي تعمل عليه فقط. عند الاقتضاء، قم بتمثيل القوى من حيث مكوناتها في الإطار المرجعي المختار. أثناء قيامك بذلك لكل قوة، قم بشطب القوة الأصلية بحيث لا تقوم بشكل خاطئ بتضمين نفس القوة مرتين في المعادلات. قم بتسمية جميع القوى - ستحتاج إلى ذلك لإجراء الحسابات الصحيحة للقوى الصافية في الاتجاهين x- و y. بالنسبة لقوة غير معروفة، يجب تحديد الاتجاه بشكل تعسفي؛ فكر في الأمر على أنه «اتجاه عملي» أو «اتجاه مشبوه». يتم تحديد الاتجاه الصحيح من خلال العلامة التي تحصل عليها في الحل النهائي. تعني علامة الجمع (+) أن اتجاه العمل هو الاتجاه الفعلي. تعني علامة الطرح (−) أن الاتجاه الفعلي معاكسٌ لاتجاه العمل المفترض. (ب) اختر موقع محور الدوران؛ وبعبارة أخرى، اختر النقطة المحورية التي ستحسب بها عزم دوران القوى العاملة. في مخطط الجسم الحر، حدد موقع المحور وأذرع الرافعة للقوى العاملة - ستحتاج إلى ذلك لإجراء الحسابات الصحيحة لعزم الدوران. عند اختيار المحور، ضع في اعتبارك أنه يمكن وضع المحور في أي مكان تريده، ولكن المبدأ التوجيهي هو أن الخيار الأفضل سيبسط قدر الإمكان حساب عزم الدوران الصافي على طول محور الدوران.
3. قم بإعداد معادلات التوازن للكائن. (أ) استخدم مخطط الجسم الحر لكتابة معادلة حالة التوازن الصحيحة 12.2.9 لمكونات القوة في الاتجاه x. (ب) استخدم مخطط الجسم الحر لكتابة معادلة حالة التوازن الصحيحة 12.2.13 لمكونات القوة في الاتجاه y. (ج) استخدم مخطط الجسم الحر لكتابة معادلة حالة التوازن الصحيحة 12.2.11 لعزم الدوران على طول محور الدوران. استخدم المعادلة 12.2.12 لتقييم مقادير العزم والحواس.
4. قم بتبسيط وحل نظام معادلات التوازن للحصول على كميات غير معروفة. في هذه المرحلة، يتضمن عملك الجبر فقط. ضع في اعتبارك أن عدد المعادلات يجب أن يكون هو نفس عدد المجاهيل. إذا كان عدد المجاهيل أكبر من عدد المعادلات، فلا يمكن حل المشكلة.
5. قم بتقييم التعبيرات للكميات غير المعروفة التي حصلت عليها في الحل الخاص بك. يجب أن تحتوي إجاباتك النهائية على قيم عددية صحيحة ووحدات مادية صحيحة. إذا لم يفعلوا ذلك، فاستخدم الخطوات السابقة لتتبع الخطأ إلى أصله وتصحيحه. يمكنك أيضًا التحقق بشكل مستقل من إجاباتك الرقمية عن طريق تحويل المحور إلى موقع مختلف وحل المشكلة مرة أخرى، وهو ما فعلناه في المثال 12.1.

لاحظ أن إعداد مخطط الجسم الحر لمشكلة توازن الجسم الصلب هو أهم مكون في عملية الحل. بدون الإعداد الصحيح والمخطط الصحيح، لن تتمكن من كتابة الشروط الصحيحة للتوازن. لاحظ أيضًا أن مخطط الجسم الحر لجسم صلب ممتد قد يخضع لحركة دورانية يختلف عن مخطط الجسم الحر للجسم الذي يختبر الحركة الانتقالية فقط (كما رأيت في الفصول الخاصة بقوانين نيوتن للحركة). في الديناميكيات الانتقالية، يتم تمثيل الجسم على أنه CM الخاص به، حيث يتم ربط جميع القوى الموجودة على الجسم ولا تظهر أي عزم دوران. هذا لا ينطبق على ديناميكيات الدوران، حيث لا يمكن تمثيل الجسم الصلب الممتد بنقطة واحدة فقط. والسبب في ذلك هو أنه عند تحليل الدوران، يجب علينا تحديد عزم الدوران الذي يعمل على الجسم، ويعتمد عزم الدوران على كل من القوة العاملة وذراع الرافعة. هنا، يساعدنا مخطط الجسم الحر لجسم صلب ممتد على تحديد عزم الدوران الخارجي.

مثال 12.3: توازن عزم الدوران

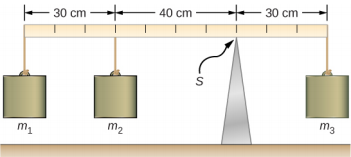
يتم ربط ثلاث كتل بعصا قياس موحدة، كما هو موضح في الشكل\(\PageIndex{1}\). كتلة عصا العداد هي 150.0 g والكتل الموجودة على يسار نقطة الارتكاز هي m ₁ = 50.0 g و m ₂ = 75.0 g، أوجد الكتلة m3 التي توازن النظام عند توصيله في الطرف الأيمن من العصا، وقوة التفاعل العادية عند نقطة الارتكاز عندما يكون النظام متوازنًا.

الشكل\(\PageIndex{1}\): في ميزان عزم الدوران، يتم دعم الشعاع الأفقي عند نقطة الارتكاز (المشار إليها بـ S) ويتم ربط الكتل بكلا جانبي نقطة الارتكاز. يكون النظام في حالة توازن ثابت عندما لا تدور الحزمة. يتم توازنه عندما يظل الشعاع مستويًا.

إستراتيجية

بالنسبة للترتيب الموضح في الشكل، نحدد القوى الخمس التالية التي تعمل على عصا العداد:

1. w ₁ = m ₁ g هو وزن الكتلة m ₁؛
2. w ₂ = m ₂ g هو وزن الكتلة m ₂؛
3. w = mg هو وزن عصا العداد بأكملها؛
4. w ₃ = m ₃ g هو وزن الكتلة غير المعروفة m ₃؛
5. F _S هي قوة رد الفعل العادية عند نقطة الدعم S.

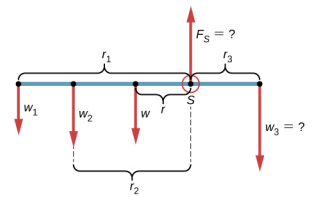
نختار إطارًا مرجعيًا يكون فيه اتجاه المحور y هو اتجاه الجاذبية، ويكون اتجاه المحور السيني على طول عصا العداد، ويكون محور الدوران (المحور z) عموديًا على المحور السيني ويمر عبر نقطة الدعم S. وبعبارة أخرى، نختار المحور عند النقطة التي يكون فيها تلمس عصا العداد الدعم. يعد هذا اختيارًا طبيعيًا للمحور لأن هذه النقطة لا تتحرك أثناء دوران العصا. نحن الآن جاهزون لإعداد مخطط الجسم الحر لعصا القياس. نشير إلى المحور ونعلق خمسة متجهات تمثل القوى الخمس على طول الخط الذي يمثل عصا العداد، ونحدد القوى بالنسبة للشكل المحوري\(\PageIndex{2}\). في هذه المرحلة، يمكننا تحديد أذرع الرافعة للقوى الخمس بالنظر إلى المعلومات المقدمة في المشكلة. بالنسبة للكتل المعلقة الثلاث، تكون المشكلة واضحة بشأن مواقعها على طول العصا، ولكن المعلومات حول موقع الوزن w تُعطى ضمنيًا. الكلمة الرئيسية هنا هي «الزي الرسمي». نعلم من دراساتنا السابقة أن CM لعصا موحدة يقع في منتصفها، لذلك هذا هو المكان الذي نعلق فيه الوزن w، عند علامة 50 سم.

الشكل\(\PageIndex{2}\): مخطط الجسم الحر لعصا القياس. يتم اختيار المحور عند نقطة الدعم S.

الحل

باستخدام الشكل\(\PageIndex{1}\) والشكل\(\PageIndex{2}\) كمرجع، نبدأ بإيجاد أذرع الرافعة للقوى الخمس المؤثرة على العصا:

\[\begin{split} r_{1} & = 30.0\; cm + 40.0\; cm = 70.0\; cm \\ r_{2} & = 40.0\; cm \\ r & = 50.0\; cm - 30.0\; cm = 20.0\; cm \\ r_{S} & = 0.0\; cm\; (because\; F_{S}\; is\; attached\; at\; the\; pivot) \\ r_{3} & = 30.0\; cm \ldotp \end{split}\]

الآن يمكننا العثور على عزم الدوران الخمسة فيما يتعلق بالمحور المختار:

\[\begin{split} \tau_{1} & = +r_{1} w_{1} \sin 90^{o} = +r_{1} m_{1} g \quad (counterclockwise\; rotation,\; positive\; sense) \\ \tau_{2} & = +r_{2} w_{2} \sin 90^{o} = +r_{2} m_{2} g \quad (counterclockwise\; rotation,\; positive\; sense) \\ \tau & = +rw \sin 90^{o} = +rmg \quad \quad \quad (gravitational\; torque) \\ \tau_{S} & = r_{S} F_{S} \sin \theta_{S} = 0 \quad \quad \quad \quad \quad (because\; r_{S} = 0\; cm) \\ \tau_{3} & = -r_{3} w_{3} \sin 90^{o} = -r_{3} m_{3} g \quad (counterclockwise\; rotation,\; negative\; sense) \end{split}\]

حالة التوازن الثانية (معادلة عزم الدوران) لعصا القياس هي

\[\tau_{1} + \tau_{2} + \tau + \tau_{S} + \tau_{3} = 0 \ldotp\]

عند استبدال قيم عزم الدوران في هذه المعادلة، يمكننا حذف عزم الدوران الذي يعطي مساهمات صفرية. بهذه الطريقة يكون شرط التوازن الثاني هو

\[+r_{1} m_{1} g + r_{2} m_{2} g + rmg - r_{3} m_{3} g = 0 \ldotp \label{12.17}\]

عند اختيار اتجاه +y ليكون موازيًا\(\vec{F}_{S}\) له، يكون شرط التوازن الأول للعصا هو

\[-w_{1} - w_{2} - w + F_{S} - w_{3} = 0 \ldotp\]

باستبدال القوى، تصبح حالة التوازن الأولى

\[-m_{1} g - m_{2} g - mg + F_{S} - m_{3} g = 0 \ldotp \label{12.18}\]

نحل هذه المعادلات في وقت واحد للقيم غير المعروفة m ₃ و F _S. في المعادلة\ ref {12.17}، نقوم بإلغاء عامل g وإعادة ترتيب المصطلحات للحصول عليها

\[r_{3} m_{3} = r_{1} m_{1} + r_{2} m_{2} + rm \ldotp\]

للحصول على m ₃، نقسم كلا الجانبين على r ₃، لذلك لدينا

\[\begin{split} m_{3} & = \frac{r_{1}}{r_{3}} m_{1} + \frac{r_{2}}{r_{3}} m_{2} + \frac{r}{r_{3}} m \\ & = \frac{70}{30} (50.0\; g) + \frac{40}{30} (75.0\; g) + \frac{20}{30} (150.0\; g) = 315.0 \left(\dfrac{2}{3}\right)\; g \simeq 317\; g \ldotp \end{split} \label{12.19}\]

للعثور على قوة التفاعل العادية، نعيد ترتيب المصطلحات في المعادلة\ ref {12.18}، وتحويل الجرام إلى الكيلوجرامات:

\[\begin{split} F_{S} & = (m_{1} + m_{2} + m + m_{3}) g \\ & = (50.0 + 75.0 + 150.0 + 316.7) \times (10^{-3}\; kg) \times (9.8\; m/s^{2}) = 5.8\; N \ldotp \end{split} \label{12.20}\]

الأهمية

لاحظ أن المعادلة\ ref {12.17} مستقلة عن قيمة g. لذلك يمكن استخدام ميزان عزم الدوران لقياس الكتلة، لأن الاختلافات في قيم g على سطح الأرض لا تؤثر على هذه القياسات. ليس هذا هو الحال بالنسبة لموازن الزنبرك لأنه يقيس القوة.

التمرين 12.3

كرر المثال 12.3 باستخدام الطرف الأيسر من عصا العداد لحساب عزم الدوران؛ أي عن طريق وضع المحور في الطرف الأيسر من عصا العداد.

في المثال التالي، نوضح كيفية استخدام شرط التوازن الأول (معادلة القوى) في الشكل المتجه المعطى بالمعادلة 12.2.9 والمعادلة 12.2.10. نقدم هذا الحل لتوضيح أهمية الاختيار المناسب للإطار المرجعي. على الرغم من أن جميع الإطارات المرجعية بالقصور الذاتي متكافئة والحلول العددية التي يتم الحصول عليها في إطار واحد هي نفسها في أي إطار آخر، فإن الاختيار غير المناسب للإطار المرجعي يمكن أن يجعل الحل طويلًا ومعقدًا، في حين أن الاختيار الحكيم للإطار المرجعي يجعل الحل بسيطًا. نعرض هذا في الحل المكافئ لنفس المشكلة. يوضح هذا المثال الخاص تطبيق التوازن الثابت على الميكانيكا الحيوية.

مثال 12.4: القوى في الساعد

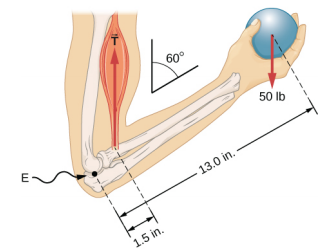
يحمل رافع الأثقال وزنًا يبلغ 50.0 رطلاً (أي ما يعادل 222.4 نيوتن) مع ساعده، كما هو موضح في الشكل\(\PageIndex{3}\). يتم وضع ساعده عند\(\beta\) = 60 درجة فيما يتعلق بالجزء العلوي من ذراعه. يتم دعم الساعد من خلال تقلص عضلة العضلة ذات الرأسين، مما يؤدي إلى عزم الدوران حول الكوع. بافتراض تأثير الشد في العضلة ذات الرأسين على طول الاتجاه الرأسي الناتج عن الجاذبية، فما مقدار الشد الذي يجب أن تمارسه العضلة لتثبيت الساعد في الموضع الموضَّح؟ ما القوة المؤثرة على مفصل المرفق؟ افترض أن وزن الساعد لا يكاد يذكر. قدم إجاباتك النهائية في وحدات SI.

الشكل\(\PageIndex{3}\): يتم تدوير الساعد حول الكوع (E) عن طريق تقلص عضلة العضلة ذات الرأسين، مما يسبب التوتر\(\vec{T}_{M}\).

إستراتيجية

نحدد ثلاث قوى تعمل على الساعد: القوة المجهولة\(\vec{F}\) في الكوع؛ والتوتر غير المعروف\(\vec{T}_{M}\) في العضلات؛ والوزن\(\vec{w}\) بحجم w = 50 رطلاً، ونعتمد الإطار المرجعي مع المحور السيني على طول الساعد والمحور عند الكوع. الاتجاه الرأسي هو اتجاه الوزن، وهو نفس اتجاه الجزء العلوي من الذراع. يصنع المحور السيني زاوية\(\beta\) = 60 درجة مع الوضع الرأسي. المحور y عمودي على المحور السيني. الآن قمنا بإعداد مخطط الجسم الحر للساعد. أولاً، نرسم المحاور والمحور والمتجهات الثلاثة التي تمثل القوى الثلاث المحددة. ثم نحدد الزاوية\(\beta\) ونمثل كل قوة بمكوني x و y، مع تذكر شطب متجه القوة الأصلي لتجنب العد المزدوج. أخيرًا، نقوم بتسمية القوى وأذرع الرافعة الخاصة بها. يظهر مخطط الجسم الحر للساعد في الشكل\(\PageIndex{4}\). في هذه المرحلة، نحن على استعداد لإعداد شروط التوازن للساعد. تحتوي كل قوة على مكونين x- و y؛ لذلك، لدينا معادلتين لشرط التوازن الأول، معادلة واحدة لكل مكون من القوة الكلية المؤثرة على الساعد.

الشكل\(\PageIndex{4}\): مخطط الجسم الحر للساعد: يقع المحور عند النقطة E (الكوع).

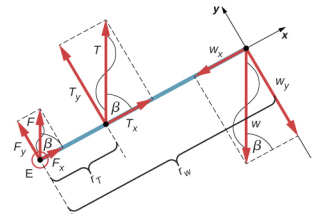
لاحظ أنه في الإطار المرجعي الخاص بنا، تأتي المساهمات في حالة التوازن الثانية (لعزم الدوران) فقط من مكونات y للقوى لأن المكونات x للقوى كلها موازية لأذرع الرافعة الخاصة بها، لذلك بالنسبة لأي منها لدينا sin\(\theta\) = 0 في المعادلة 12.2.12. بالنسبة لمكونات y، لدينا\(\theta\) = ± 90 درجة في المعادلة 12.2.12. لاحظ أيضًا أن عزم القوة عند الكوع هو صفر لأن هذه القوة متصلة بالمحور. لذا فإن المساهمة في عزم الدوران الصافي تأتي فقط من عزم دوران T _y و w _y.

الحل

نرى من مخطط الجسم الحر أن المكون x للقوة الكلية يفي بالمعادلة

\[+F_{x} + T_{x} - w_{x} = 0 \label{12.21}\]

ويلبي المكون y من القوة الصافية

\[+F_{y} + T_{y} - w_{y} = 0 \ldotp \label{12.22}\]

المعادلة\ ref {12.21} والمعادلة\ ref {12.22} هما معادلتان لشرط التوازن الأول (للقوى). بعد ذلك، نقرأ من مخطط الجسم الحر أن عزم الدوران الصافي على طول محور الدوران هو

\[+r_{T} T_{y} - r_{w} w_{y} = 0 \ldotp \label{12.23}\]

المعادلة\ ref {12.23} هي حالة التوازن الثانية (لعزم الدوران) للساعد. يُظهر مخطط الجسم الحر أن أذرع الرافعة هي r _T = 1.5 بوصة. و r _w = 13.0 بوصة. في هذه المرحلة، لا نحتاج إلى تحويل البوصات إلى وحدات SI، لأنه طالما أن هذه الوحدات متسقة في المعادلة 12.23، فإنها تلغى. باستخدام مخطط الجسم الحر مرة أخرى، نجد مقادير القوى المكونة:

\[\begin{split} F_{x} & = F \cos \beta = F \cos 60^{o} = \frac{F}{2} \\ T_{x} & = T \cos \beta = T \cos 60^{o} = \frac{T}{2} \\ w_{x} & = w \cos \beta = w \cos 60^{o} = \frac{w}{2} \\ F_{y} & = F \sin \beta = F \sin 60^{o} = \frac{F \sqrt{3}}{2} \\ T_{y} & = T \sin \beta = T \sin 60^{o} = \frac{T \sqrt{3}}{2} \\ w_{y} & = w \sin \beta = w \sin 60^{o} = \frac{w \sqrt{3}}{2} \ldotp \end{split}\]

نستبدل هذه المقادير بالمعادلة\ ref {12.21}، المعادلة\ المرجع {12.22}، والمعادلة\ المرجع {12.23} للحصول، على التوالي،

\[\begin{split} \frac{F}{2} + \frac{T}{2} - \frac{w}{2} & = 0 \\ \frac{F \sqrt{3}}{2} + \frac{T \sqrt{3}}{2} - \frac{w \sqrt{3}}{2} & = 0 \\ \frac{r_{T} T \sqrt{3}}{2} - \frac{r_{w} w \sqrt{3}}{2} & = 0 \ldotp \end{split}\]

عندما نبسط هذه المعادلات، نرى أنه لم يتبق لنا سوى معادلتين مستقلتين لمقاييس القوة غير المعروفة، F و T، لأن المعادلة\ ref {12.21} للمكون x تعادل المعادلة\ ref {12.22} للمكون y. بهذه الطريقة نحصل على شرط التوازن الأول للقوى

\[F + T - w = 0 \label{12.24}\]

وحالة التوازن الثانية لعزم الدوران

\[r_{T} T - r_{w} w = 0 \ldotp \label{12.25}\]

يتم الحصول على حجم التوتر في العضلات من خلال حل المعادلة\ ref {12.25}:

\[T = \frac{r_{w}}{r_{T}} w =frac{13.0}{1.5} (50\; lb) = 433 \frac{1}{3}\; lb \simeq 433.3\; lb \ldotp\]

يتم الحصول على القوة عند الكوع من خلال حل المعادلة\ ref {12.24}:

\[F = w - T = 50.0\; lb - 433.3\; lb = -383.3\; lb \ldotp\]

تخبرنا العلامة السالبة في المعادلة أن القوة الفعلية عند الكوع تتعارض مع اتجاه العمل المعتمد لرسم مخطط الجسم الحر. في الإجابة النهائية، نقوم بتحويل القوى إلى وحدات قوة SI. الجواب هو

\[F = 383.3\; lb = 383.3(4.448\; N) = 1705\; N\; downward\]

\[T = 433.3\; lb = 433.3(4.448\; N) = 1927\; N\; upward \ldotp\]

الأهمية

هناك مسألتان مهمتان هنا جديرتان بالملاحظة. يتعلق الأول بالتحويل إلى وحدات SI، وهو ما يمكن القيام به في نهاية الحل طالما أننا نحافظ على الاتساق في الوحدات. القضية الثانية المهمة تتعلق بالمفاصل المفصلية مثل الكوع. في التحليل الأولي للمشكلة، يجب دائمًا افتراض أن المفاصل المفصلية تمارس قوة في اتجاه تعسفي، ومن ثم يجب عليك حل جميع مكونات قوة المفصلة بشكل مستقل. في هذا المثال، تكون قوة الكوع عمودية لأن المشكلة تفترض أن شد العضلة ذات الرأسين عمودي أيضًا. ومع ذلك، فإن هذا التبسيط ليس قاعدة عامة.

الحل 2

لنفترض أننا نعتمد إطارًا مرجعيًا مع اتجاه المحور y على طول وزن 50 رطلاً والمحور الموضوع عند الكوع. في هذا الإطار، تحتوي جميع القوى الثلاث على مكونات y فقط، لذلك لدينا معادلة واحدة فقط لشرط التوازن الأول (للقوى). نرسم مخطط الجسم الحر للساعد كما هو موضح في الشكل\(\PageIndex{5}\)، مع الإشارة إلى المحور والقوى العاملة وأذرع الرافعة فيما يتعلق بالمحور\(\theta_{T}\) والزوايا\(\theta_{w}\) التي تصنعها القوى\(\vec{T}_{M}\)\(\vec{w}\) (على التوالي) بأذرع الرافعة. في تعريف عزم الدوران المعطى بالمعادلة 12.2.12،\(\theta_{T}\) تكون الزاوية هي زاوية اتجاه المتجه\(\vec{T}_{M}\)، ويتم حسابها بعكس اتجاه عقارب الساعة من الاتجاه الشعاعي لذراع الرافعة الذي يشير دائمًا بعيدًا عن المحور. وفقًا لنفس الاتفاقية،\(\theta_{w}\) يتم قياس الزاوية بعكس اتجاه عقارب الساعة من الاتجاه الشعاعي لذراع الرافعة إلى المتجه\(\vec{w}\). بهذه الطريقة، يتم حساب عزم الدوران غير الصفري بسهولة عن طريق الاستبدال المباشر للمعادلة 12.2.12 على النحو التالي:

\[\tau_{T} = r_{T} T \sin \theta_{T} = r_{T} T \sin \beta = r_{T} T \sin 60^{o} = + \frac{r_{T} T \sqrt{3}}{2}\]

\[\tau_{w} = r_{w} w \sin \theta_{w} = r_{w} w \sin (\beta + 180^{o}) = -r_{w} w \sin \beta = - \frac{r_{w} w \sqrt{3}}{2} \ldotp\]

الشكل\(\PageIndex{5}\): مخطط الجسم الحر للساعد للحل المكافئ. يقع المحور عند النقطة E (الكوع).

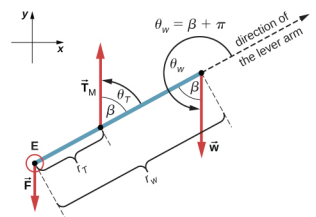
يمكن الآن كتابة حالة التوازن الثانية،\(\tau_{T}\) +\(\tau_{w}\) = 0، كـ

\[\frac{r_{T} T \sqrt{3}}{2} - \frac{r_{w} w \sqrt{3}}{2} = 0 \ldotp \label{12.26}\]

من مخطط الجسم الحر، فإن حالة التوازن الأولى (للقوى) هي

\[-F + T - w = 0 \ldotp \label{12.27}\]

المعادلة\ ref {12.26} مطابقة للمعادلة\ المرجع {12.25} وتعطي النتيجة T = 433.3 lb. المعادلة\ ref {12.27} تعطي

\[F = T - w = 433.3\; lb - 50.0\; lb = 383.3\; lb\]

نرى أن هذه الإجابات مطابقة لإجاباتنا السابقة، ولكن الخيار الثاني للإطار المرجعي يؤدي إلى حل مكافئ أبسط وأسرع لأنه لا يتطلب حل القوى في مكوناتها المستطيلة.

التمرين 12.4

كرر المثال 12.4 بافتراض أن الساعد هو كائن ذو كثافة موحدة يزن 8.896 نيوتن.

مثال 12.5: سلم يستقر على الحائط

سلم منتظم طوله = 5.0 متر ووزنه 400.0 نيوتن، ويستقر السلم على جدار عمودي زلق، كما هو موضح في الشكل\(\PageIndex{6}\). زاوية الميل بين السلم والأرضية الخشنة هي\(\beta\) = 53 درجة. أوجد قوى التفاعل من الأرض ومن الجدار على السلم ومعامل الاحتكاك الإستاتيكي\(\mu_{s}\) عند واجهة السلم مع الأرضية التي تمنع السلم من الانزلاق.

الشكل\(\PageIndex{6}\) أ سلم بطول 5.0 متر يقع على جدار غير قابل للاحتكاك.

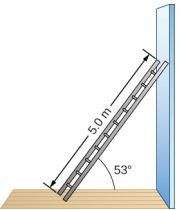
إستراتيجية

يمكننا تحديد أربع قوى تعمل على السلم. القوة الأولى هي قوة التفاعل العادية N من الأرض في الاتجاه الرأسي التصاعدي. القوة الثانية هي قوة الاحتكاك الثابتة f =\(\mu_{s}\) N الموجهة أفقيًا على طول الأرض نحو الجدار - هذه القوة تمنع السلم من الانزلاق. تعمل هاتان القوتان على السلم عند نقطة التلامس مع الأرض. القوة الثالثة هي وزن السلم w، المثبت عند CM الموجود في منتصف المسافة بين طرفيه. القوة الرابعة هي قوة رد الفعل العادية F من الجدار في الاتجاه الأفقي بعيدًا عن الجدار، والمثبتة عند نقطة الاتصال بالجدار. لا توجد قوى أخرى لأن الجدار زلق، مما يعني عدم وجود احتكاك بين الجدار والسلم. بناءً على هذا التحليل، نعتمد الإطار المرجعي مع المحور y في الاتجاه الرأسي (الموازي للجدار) والمحور السيني في الاتجاه الأفقي (الموازي للأرضية). في هذا الإطار، تحتوي كل قوة إما على مكون أفقي أو مكون عمودي ولكن ليس كلاهما، مما يبسط الحل. نختار المحور عند نقطة الاتصال مع الأرضية. في مخطط الجسم الحر للسلم، نشير إلى المحور والقوى الأربع وأذرع الرافعة والزوايا بين أذرع الرافعة والقوى، كما هو موضح في الشكل\(\PageIndex{7}\). من خلال اختيارنا للموقع المحوري، لا يوجد عزم دوران سواء من قوة التفاعل العادية N أو من الاحتكاك الثابت f لأن كلاهما يعمل في المحور.

الشكل\(\PageIndex{7}\): رسم تخطيطي للجسم الحر لسلم يرتكز على جدار خالٍ من الاحتكاك.

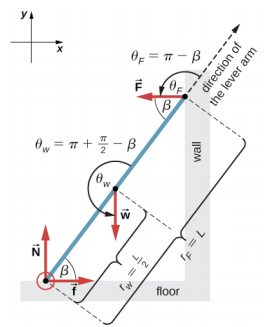
الحل

من مخطط الجسم الحر، القوة الكلية في الاتجاه x هي

\[+f - F = 0 \label{12.28}\]

القوة الصافية في الاتجاه y هي

\[+ N - w = 0 \label{12.29}\]

وعزم الدوران الصافي على طول محور الدوران عند النقطة المحورية هو

\[\tau_{w} + \tau_{F} = 0 \ldotp \label{12.30}\]

أين\(\tau_{w}\) هو عزم الدوران للوزن w\(\tau_{F}\) وهو عزم التفاعل F. من مخطط الجسم الحر، نحدد أن ذراع الرافعة للتفاعل عند الجدار هو r _F = L = 5.0 m وذراع الرافعة للوزن هو r _w\(\frac{L}{2}\) = = 2.5 m بمساعدة مخطط الجسم الحر، نحدد الزوايا المراد استخدامها في المعادلة 12.2.12 لعزم الدوران:\(\theta_{F}\) = 180 درجة -\(\beta\) لعزم الدوران من قوة التفاعل مع الجدار، و\(\theta_{w}\) = 180°+ (90° −\(\beta\)) لعزم الدوران بسبب الوزن. نحن الآن جاهزون لاستخدام المعادلة 12.2.12 لحساب عزم الدوران:

\[\tau_{w} = r_{w} w \sin \theta_{w} = r_{w} w \sin (180^{o} + 90^{o} - \beta) = - \frac{L}{2} w \sin (90^{o} - \beta) = - \frac{L}{2} w \cos \beta\]

\[tau_{F} = r_{F} F \sin \theta_{F} = r_{F} F \sin (180^{o} - \beta) = LF \sin \beta \ldotp\]

نستبدل عزم الدوران في المعادلة\ ref {12.30} ونحل بـ F:

\[- \frac{L}{2} w \cos \beta + LF \sin \beta = 0 \label{12.31}\]

\[F = \frac{w}{2} \cot \beta = \frac{400.0\; N}{2} \cot 53^{o} = 150.7\; N\]

نحصل على قوة التفاعل العادية مع الأرض عن طريق حل المعادلة\ المرجع {12.29}: N = w = 400.0 N. يتم الحصول على مقدار الاحتكاك بحل المعادلة\ ref {12.28}: f = F = 150.7 N. معامل الاحتكاك الإستاتيكي هو\(\mu_{s}\) =\(\frac{f}{N}\) =\(\frac{150.7}{400.0}\) = 0.377.

القوة الصافية على السلم عند نقطة التلامس مع الأرض هي المجموع المتجه للتفاعل الطبيعي من الأرض وقوى الاحتكاك الإستاتيكية:

\[\vec{F}_{floor} = \vec{f} + \vec{N} = (150.7\; N)(- \hat{i}) + (400.0\; N)(+ \hat{j}) = (-150.7\; \hat{i} + 400.0\; \hat{j}) N \ldotp\]

حجمه هو

\[F_{floor} = \sqrt{f^{2} + N^{2}} = \sqrt{150.7^{2} + 400.0^{2}}\; N = 427.4\; N\]

واتجاهها هو

\[\varphi = \tan^{-1} \left(\dfrac{N}{f}\right) = \tan^{-1} \left(\dfrac{400.0}{150.7}\right) = 69.3^{o}\; above\; the\; floor \ldotp\]

يجب أن نؤكد هنا على ملاحظتين عامتين للاستخدام العملي. أولاً، لاحظ أنه عندما نختار نقطة محورية، ليس هناك توقع بأن النظام سوف يتمحور فعليًا حول النقطة المختارة. السلم في هذا المثال لا يدور على الإطلاق ولكنه يقف بثبات على الأرض؛ ومع ذلك، فإن نقطة التلامس مع الأرض تعد اختيارًا جيدًا للمحور. ثانيًا، لاحظ عندما نستخدم المعادلة 12.2.12 لحساب عزم الدوران الفردي، لا نحتاج إلى حل القوى في مكوناتها العادية والمتوازية فيما يتعلق باتجاه ذراع الرافعة، ولا نحتاج إلى التفكير في الإحساس بعزم الدوران. طالما تم تحديد الزاوية في المعادلة 12.2.12 بشكل صحيح - بمساعدة مخطط الجسم الحر - كالزاوية المقاسة بعكس اتجاه عقارب الساعة من اتجاه ذراع الرافعة إلى اتجاه متجه القوة، فإن المعادلة 12.2.12 تعطي كلاً من مقدار العزم وإحساسه. ويرجع ذلك إلى أن عزم الدوران هو المنتج المتجه لمتجه ذراع الرافعة المتقاطع مع متجه القوة، وتعبر المعادلة 12.2.12 عن المكون المستطيل لمنتج المتجه هذا على طول محور الدوران.

الأهمية

هذه النتيجة مستقلة عن طول السلم لأنه يتم إلغاء L في حالة التوازن الثانية، المعادلة\ ref {12.31}. بغض النظر عن طول السلم أو قصره، طالما أن وزنه 400 نيوتن والزاوية مع الأرض هي 53 درجة، فإن نتائجنا ثابتة. لكن السلم سينزلق إذا أصبح عزم الدوران الصافي سالبًا في المعادلة\ ref {12.31}. يحدث هذا لبعض الزوايا عندما لا يكون معامل الاحتكاك الساكن كبيرًا بما يكفي لمنع السلم من الانزلاق.

التمرين 12.5

بالنسبة للحالة الموضحة في المثال 12.5، حدد قيم معامل الاحتكاك الإستاتيكي الذي يبدأ السلم بالانزلاق\(\mu_{s}\) من أجله، علمًا بأن β هي الزاوية التي يصنعها السلم مع الأرضية.

مثال 12.6: القوى على مفصلات الأبواب

يتم دعم الباب المتأرجح الذي يزن w = 400.0 N بمفصلات A و B بحيث يمكن للباب أن يتأرجح حول محور عمودي يمر عبر المفصلات الشكل\(\PageIndex{8}\). يبلغ عرض الباب b = 1.00 m، ولبلاطة الباب كثافة كتلة موحدة. يتم وضع المفصلات بشكل متماثل على حافة الباب بحيث يتم توزيع وزن الباب بالتساوي بينهما. يتم فصل المفصلات بالمسافة a = 2.00 m، أوجد القوى الموجودة على المفصلات عندما يكون الباب نصف مفتوح.

الشكل\(\PageIndex{8}\): الباب العمودي المتأرجح 400-N مدعوم بمفصلين متصلين عند النقطتين A و B.

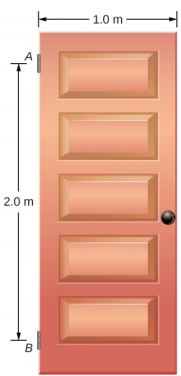
إستراتيجية

يمكن العثور على القوى التي يمارسها الباب على مفصلاته ببساطة عن طريق عكس اتجاهات القوى التي تمارسها المفصلات على الباب. ومن ثم، فإن مهمتنا هي العثور على القوى من المفصلات على الباب. تعمل ثلاث قوى على لوح الباب: قوة غير معروفة\(\vec{A}\) من المفصلة A، وقوة غير معروفة\(\vec{B}\) من المفصلة B، والوزن المعروف\(\vec{w}\) المرفق في مركز كتلة لوح الباب. يقع CM في المركز الهندسي للباب لأن البلاطة لها كثافة كتلة موحدة. نعتمد إطارًا مرجعيًا مستطيلًا مع المحور y على طول اتجاه الجاذبية والمحور السيني في مستوى البلاطة، كما هو موضح في اللوحة (أ) من الشكل\(\PageIndex{9}\)، ونقوم بحل جميع القوى في مكوناتها المستطيلة. بهذه الطريقة، لدينا أربع قوى مكونة غير معروفة: عنصران للقوة\(\vec{A}\) (A _x و A _y)، ومكونان للقوة\(\vec{B}\) (B _x و B _y). في مخطط الجسم الحر، نمثل القوتين عند المفصلات بواسطة مكونات المتجهات، التي تكون توجهاتها المفترضة عشوائية. نظرًا لوجود أربعة معادلات مجهولة (A _x و B _x و A _y و B _y)، يجب علينا إعداد أربع معادلات مستقلة. المعادلة الأولى هي حالة توازن القوى في الاتجاه x. المعادلة الثانية هي حالة توازن القوى في الاتجاه y. المعادلة الثالثة هي حالة توازن عزم الدوران في الدوران حول المفصلة. نظرًا لتوزيع الوزن بالتساوي بين المفصلات، لدينا المعادلة الرابعة، A _y = B _y. لإعداد ظروف التوازن، نرسم مخططًا للجسم الحر ونختار النقطة المحورية في المفصلة العلوية، كما هو موضح في اللوحة (ب) من الشكل\(\PageIndex{9}\). أخيرًا، نحل معادلات مكونات القوة غير المعروفة ونجد القوى.

الشكل\(\PageIndex{9}\): (أ) الهندسة و (ب) مخطط الجسم الحر للباب.

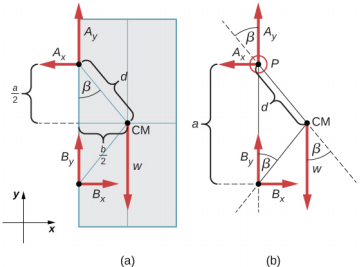
الحل

من مخطط الجسم الحر للباب، لدينا شرط التوازن الأول للقوى:

في الاتجاه السيني، $-A_ {x} + B_ {x} = 0\ السهم الأيمن A_ {x} + B_ {x} $$في اتجاه Y، $+ A_ {y} + B_ {y} - w = 0\ السهم الأيمن A_ {y} = B_ {y} = B_ {y} =\ frac {y} {2} =\ frac {400.0\; N} {2}} = 200.0\; N\ ldotp\]

نختار المحور عند النقطة P (المفصلة العلوية، وفقًا لمخطط الجسم الحر) ونكتب حالة التوازن الثانية لعزم الدوران في الدوران حول النقطة P:

المحور عند P: $$\ tau_ {w} +\ tau_ {Bx} +\ tau_ {By} = 0\ ldotp\ label {12.32}\]

نستخدم مخطط الجسم الحر للعثور على جميع المصطلحات في هذه المعادلة:

\[\begin{split} \tau_{w} & = dw \sin (- \beta) = -dw \sin \beta = -dw \frac{\frac{b}{2}}{d} = -w \frac{b}{2} \\ \tau_{Bx} & = a B_{x} \sin 90^{o} = + a B_{x} \\ \tau_{By} & = a B_{y} \sin 180^{o} = 0 \ldotp \end{split}\]

في تقييم الخطيئة\(\beta\)، نستخدم هندسة المثلث الموضح في الجزء (أ) من الشكل. الآن نستبدل عزم الدوران هذه بالمعادلة\ ref {12.32} ونحسب B _x:

محور في P: $-w\ frac {b} {2} + A B_ {x} = 0\ السهم الأيمن B_ {x} = w\ frac {b} {2a} = (400.0\; N)\ frac {1} {2\;\ cdotp 2} = 100.0\; N\ ldotp\]

لذلك فإن مقادير قوى المكون الأفقي هي A _x = B _x = 100.0 N. القوى الموجودة على الباب هي

في المفصلة العلوية: $$\ vec {F} _ {A\; على\; الباب} = -100.0\; N\;\ قبعة {i} + 200.0\; N\;\ قبعة {j} $$عند المفصلة السفلية: $\ vec {F} _ {B;; على\; الباب} = +100.0\; N\;\ قبعة {i} + 200.0\; N\;\\ قبعة {i} + 200.0\;\\\ قبعة {j}\ ldotp\]

تم العثور على القوى الموجودة على المفصلات من قانون نيوتن الثالث كـ

على المفصلة العلوية: $$\ vec {F} _ {الباب\; على\; A} = 100.0\; N\;\ القبعة {i} - 200.0\; N\;\ القبعة {j} $$على المفصلة السفلية: $\ vec {F} _ {\;; على\; B} = - 100.0\; N\;\ قبعة {i} - 200.0\; N\;\\ قبعة {i} - 200.0\;\\\ قبعة {j}\ ldotp\]

الأهمية

لاحظ أنه إذا تمت صياغة المشكلة دون افتراض توزيع الوزن بالتساوي بين المفصلين، فلن نتمكن من حلها لأن عدد المجاهيل سيكون أكبر من عدد المعادلات التي تعبر عن ظروف التوازن.

التمرين 12.6

حل المشكلة في المثال 12.6 عن طريق أخذ الموضع المحوري في مركز الكتلة.

التمرين 12.7

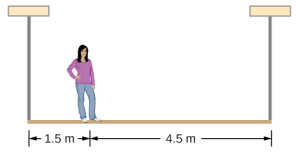
يقف شخص وزنه ٥٠ كجم على بُعد ١٫٥ مترًا من أحد طرفي سقالة موحدة طولها ٦٫٠ م وكتلتها ٧٠٫٠ كجم. ابحث عن التوترات في الحبلين العموديين الداعمين للسقالة.

التمرين 12.8

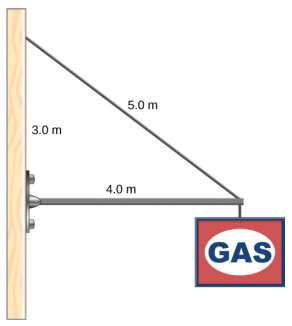
علامة 400.0-N معلقة من نهاية الدعامة الموحدة. يبلغ طول الدعامة 4.0 أمتار ويزن 600.0 نيوتن، ويتم دعم الدعامة بمفصلة على الحائط وكابل يتم ربط طرفه الآخر بالحائط عند نقطة أعلى 3.0 متر من الطرف الأيسر من الدعامة. ابحث عن الشد في الكبل الداعم وقوة المفصلة على الدعامة.