12.2: شروط التوازن الثابت
- Page ID
- 200009
- حدد الظروف المادية للتوازن الثابت.
- ارسم مخططًا للجسم الحر لجسم صلب تعمل عليه القوى.
- اشرح كيف تسمح لنا شروط التوازن بحل المسائل الإحصائية.
نقول أن الجسم الصلب في حالة توازن عندما يكون كل من التسارع الخطي والزاوي صفرًا بالنسبة للإطار المرجعي بالقصور الذاتي. هذا يعني أن الجسم في حالة التوازن يمكن أن يتحرك، ولكن إذا كان الأمر كذلك، يجب أن تكون سرعاته الخطية والزاوية ثابتة. نقول أن الجسم الصلب في حالة توازن ثابت عندما يكون في حالة سكون في الإطار المرجعي المحدد. لاحظ أن التمييز بين حالة الراحة وحالة الحركة المنتظمة هو تمييز مصطنع - أي أن الجسم قد يكون في حالة سكون في الإطار المرجعي الذي اخترناه، ولكن بالنسبة للراصد الذي يتحرك بسرعة ثابتة بالنسبة لإطارنا، يبدو أن نفس الكائن في حركة موحدة بسرعة ثابتة. ولأن الحركة نسبية، فإن ما هو في حالة توازن ثابت بالنسبة لنا هو في حالة توازن ديناميكي للراصد المتحرك، والعكس صحيح. نظرًا لأن قوانين الفيزياء متطابقة لجميع الأطر المرجعية بالقصور الذاتي، في الإطار المرجعي بالقصور الذاتي، لا يوجد فرق بين التوازن الثابت والتوازن.
وفقًا لقانون نيوتن الثاني للحركة، يحدث التسارع الخطي لجسم جامد بسبب قوة صافية تؤثر عليه، أو
\[\sum_{k} \vec{F}_{k} = m \vec{a}_{CM} \ldotp \label{12.1}\]
هنا، مجموع كل القوى الخارجية المؤثرة على الجسم، حيث m هي كتلته وهو التسارع الخطي لمركز كتلته (\(\vec{a}_{CM}\)وهو مفهوم ناقشناه في الزخم الخطي والتصادمات على الزخم الخطي والاصطدامات). في حالة الاتزان، يكون التسارع الخطي صفرًا. إذا قمنا بتعيين التسارع إلى الصفر في المعادلة\ ref {12.1}، نحصل على المعادلة التالية:
تعبر حالة التوازن الأولى للتوازن الثابت للجسم الصلب عن التوازن الانتقالي:
\[\sum_{k} \vec{F}_{k} = \vec{0} \ldotp \label{12.2}\]
حالة التوازن الأولى، المعادلة\ ref {12.2}، هي حالة توازن القوى، التي واجهناها عند دراسة تطبيقات قوانين نيوتن.
تعادل معادلة المتجهات هذه المعادلات العددية الثلاث التالية لمكونات القوة الصافية:
\[\sum_{k} F_{kx} = 0,\; \sum_{k} F_{ky} = 0,\; \sum_{k} F_{kz} = 0 \ldotp \label{12.3}\]
على غرار المعادلة\ ref {12.1}، يمكننا القول أن التسارع\(\vec{\alpha}\) الدوراني لجسم صلب حول محور دوران ثابت ناتج عن عزم الدوران الصافي الذي يؤثر على الجسم، أو
\[\sum_{k} \vec{\tau}_{k} = I \vec{\alpha} \ldotp \label{12.4}\]
ها هو القصور الدوراني للجسم أثناء الدوران حول هذا المحور ويكون التجميع فوق كل عزم\(\vec{\tau}_{k}\) دوران القوى الخارجية في المعادلة\ ref {12.2}. في حالة التوازن، يكون التسارع الدوراني صفرًا. من خلال ضبط الجانب الأيمن من المعادلة على الصفر\ ref {12.4}، نحصل على شرط التوازن الثاني:
تعبر حالة التوازن الثانية للتوازن الثابت للجسم الصلب عن التوازن الدوراني:
\[\sum_{k} \vec{\tau}_{k} = \vec{0} \ldotp \label{12.5}\]
حالة التوازن الثانية، المعادلة\ ref {12.5}، هي حالة توازن عزم الدوران التي واجهناها عندما درسنا ديناميكيات الدوران. تجدر الإشارة إلى أن معادلة التوازن هذه صالحة عمومًا للتوازن الدوراني حول أي محور دوران (ثابت أو غير ذلك). مرة أخرى، تعادل معادلة المتجهات هذه ثلاث معادلات قياسية للمكونات المتجهة لعزم الدوران الصافي:
\[\sum_{k} \tau_{kx} = 0,\; \sum_{k} \tau_{ky} = 0,\; \sum_{k} \tau_{kz} = 0 \ldotp \label{12.6}\]
تعني حالة التوازن الثانية أنه في حالة التوازن، لا يوجد عزم دوران خارجي صافي للتسبب في الدوران حول أي محور. يتم ذكر شروط التوازن الأولى والثانية في إطار مرجعي معين. يتضمن الشرط الأول القوى فقط وبالتالي فهو مستقل عن أصل الإطار المرجعي. ومع ذلك، فإن الشرط الثاني يتضمن عزم الدوران، الذي يُعرّف بأنه منتج متقاطع\(\vec{\tau}_{k} = \vec{r}_{k} \times \vec{F}_{k}\)، حيث يدخل متجه الموضع فيما يتعلق\(\vec{r}_{k}\) بمحور دوران النقطة التي يتم فيها تطبيق القوة في المعادلة. لذلك، يعتمد عزم الدوران على موقع المحور في الإطار المرجعي. ومع ذلك، عندما تستقر ظروف التوازن الدوراني والانتقالي في وقت واحد في إطار مرجعي واحد، فإنها تبقى أيضًا في أي إطار مرجعي آخر بالقصور الذاتي، بحيث يظل عزم الدوران الصافي حول أي محور دوران صفرًا. تفسير ذلك واضح إلى حد ما.
لنفترض أن المتجه\(\vec{R}\) هو موضع أصل إطار مرجعي جديد بالقصور الذاتي S في الإطار المرجعي القديم بالقصور الذاتي S. من خلال دراستنا للحركة النسبية، نعلم أنه في الإطار المرجعي الجديد S ′، يكون متجه\(\vec{r}′_{k}\) موضع النقطة التي يتم فيها تطبيق القوة\(\vec{F}_{k}\) هو متعلق بـ\(\vec{r}_{k}\) عبر المعادلة
\[\vec{r}'_{k} = \vec{r}_{k} - \vec{R} \ldotp\]
الآن، يمكننا جمع كل عزم الدوران\(\vec{\tau}'_{k} = \vec{r}'_{k} \times \vec{F}_{k}\) لجميع القوى الخارجية في إطار مرجعي جديد، S':
\[\sum_{k} \vec{\tau}'_{k} = \sum_{k} \vec{r}'_{k} \times \vec{F}_{k} = \sum_{k} (\vec{r}_{k} - \vec{R}) \times \vec{F}_{k} = \sum_{k} \vec{r}_{k} \times \vec{F}_{k} - \sum_{k} \vec{R} \times \vec{F}_{k} = \sum \vec{\tau}_{k} - \vec{R} \times \sum_{k} \vec{F}_{k} = \vec{0} \ldotp\]
في الخطوة الأخيرة من سلسلة التفكير هذه، استخدمنا حقيقة أنه في حالة التوازن في الإطار المرجعي القديم، S، يختفي المصطلح الأول بسبب المعادلة\ ref {12.5} ويختفي المصطلح الثاني بسبب المعادلة\ ref {12.2}. وبالتالي، نرى أن عزم الدوران الصافي في أي إطار بالقصور الذاتي المرجعي S ′ هو صفر، بشرط أن يثبت كلا الشرطين للتوازن في إطار مرجعي بالقصور الذاتي\ ref {S}.
المعنى العملي لذلك هو أنه عند تطبيق شروط التوازن لجسم صلب، فإننا أحرار في اختيار أي نقطة كأصل للإطار المرجعي. يتم تحديد اختيارنا للإطار المرجعي من خلال التفاصيل المادية للمشكلة التي نقوم بحلها. في إطار مرجعي واحد، قد يكون الشكل الرياضي لظروف التوازن معقدًا جدًا، بينما في إطار آخر، قد تحتوي نفس الشروط على شكل رياضي أبسط يسهل حله. يُطلق على أصل الإطار المرجعي المحدد اسم النقطة المحورية.
في الحالة الأكثر عمومية، يتم التعبير عن ظروف التوازن من خلال المعادلات العددية الستة (المعادلات\ ref {12.3} و\ ref {12.6}). بالنسبة لمشاكل التوازن المستوي مع الدوران حول محور ثابت، والتي نأخذها في الاعتبار في هذا الفصل، يمكننا تقليل عدد المعادلات إلى ثلاثة. يتمثل الإجراء القياسي في اعتماد إطار مرجعي حيث يكون المحور z هو محور الدوران. مع هذا الاختيار للمحور، يحتوي عزم الدوران الصافي على مكون z فقط، وتقع جميع القوى التي تحتوي على عزم دوران غير صفري في المستوى xy، وبالتالي فإن المساهمات في عزم الدوران الصافي تأتي فقط من مكونات x- و y للقوى الخارجية. وبالتالي، بالنسبة للمشاكل المستوية ذات محور الدوران العمودي على المستوى السيني، لدينا شروط التوازن الثلاثة التالية للقوى وعزم الدوران:
\[F_{1x} + F_{2x} + \cdots + F_{Nx} = 0 \label{12.7}\]
\[F_{1y} + F_{2y} + \cdots + F_{Ny} = 0 \label{12.8}\]
\[\tau_{1} + \tau_{2} + \cdots + \tau_{N} = 0 \label{12.9}\]
حيث يكون المجموع فوق جميع القوى الخارجية N التي تعمل على الجسم وعلى عزم الدوران. في المعادلة\ ref {12.9}، قمنا بتبسيط الترميز بإسقاط الرمز z، لكننا نفهم هنا أن المجموع يشمل جميع المساهمات على طول المحور z، وهو محور الدوران. في المعادلة\ ref {12.9}، يكون المكون z لعزم الدوران\(\vec{\tau}_{k}\) من القوة\(\vec{F}_{k}\) هو
\[\tau_{k} = r_{k} F_{k} \sin \theta \label{12.10}\]
حيث r k هو طول ذراع الرافعة للقوة و F k هو حجم القوة (كما رأيت في دوران المحور الثابت). الزاوية\(\theta\) هي الزاوية بين المتجهات\(\vec{r}_{k}\) والقياس\(\vec{F}_{k}\) من متجه\(\vec{r}_{k}\) إلى متجه\(\vec{F}_{k}\) في اتجاه عكس عقارب الساعة (الشكل\(\PageIndex{1}\)). عند استخدام Equation\ ref {12.10}، غالبًا ما نحسب حجم عزم الدوران ونعين إحساسه إما إيجابيًا (+) أو سالبًا (−)، اعتمادًا على اتجاه الدوران الناتج عن عزم الدوران هذا وحده. في المعادلة\ ref {12.9}، عزم الدوران الصافي هو مجموع المصطلحات، مع حساب كل مصطلح من المعادلة\ ref {12.10}، ويجب أن يكون لكل مصطلح المعنى الصحيح. وبالمثل، في المعادلة\ ref {12.7}، نقوم بتعيين علامة + لفرض المكونات في اتجاه + x وعلامة − للمكونات في اتجاه − x. يجب اتباع نفس القاعدة باستمرار في المعادلة\ ref {12.8}، عند حساب مكونات القوة على طول المحور y.
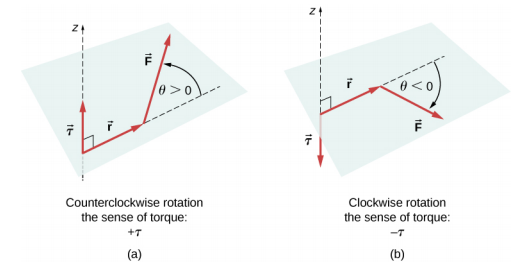
شاهد هذا العرض التوضيحي لرؤية قوتين تؤثران على مربع صلب في بعدين. في جميع الأوقات، يتم استيفاء شروط التوازن الثابت التي قدمتها المعادلة\ ref {12.7} من خلال المعادلة\ المرجع {12.9}. يمكنك تغيير مقادير القوى وأذرع الرافعة الخاصة بها ومراقبة تأثير هذه التغييرات على المربع.
في العديد من حالات التوازن، تكون إحدى القوى المؤثرة على الجسم هي وزنه. في مخططات الجسم الحر، يتم ربط ناقل الوزن بمركز ثقل الجسم. لجميع الأغراض العملية، يتطابق مركز الجاذبية مع مركز الكتلة، كما تعلمت في كتاب الزخم الخطي والتصادمات حول الزخم الخطي والاصطدامات. فقط في الحالات التي يكون فيها للجسم امتداد مكاني كبير بحيث يكون مجال الجاذبية غير منتظم في جميع أنحاء حجمه، يقع مركز الجاذبية ومركز الكتلة في نقاط مختلفة. ولكن في الحالات العملية، حتى الأجسام الكبيرة مثل المباني أو السفن السياحية توجد في مجال جاذبية منتظم على سطح الأرض، حيث يكون التسارع الناتج عن الجاذبية ثابتًا قدره g = 9.8 m/s 2. في هذه الحالات، يكون مركز الجاذبية مطابقًا لمركز الكتلة. لذلك، خلال هذا الفصل، نستخدم مركز الكتلة (CM) كنقطة يتم فيها ربط متجه الوزن. تذكر أن CM له معنى فيزيائي خاص: عندما يتم تطبيق قوة خارجية على الجسم عند قياسه بالضبط، يخضع الجسم ككل لحركة انتقالية ولا تتسبب هذه القوة في الدوران.
عندما يقع CM خارج محور الدوران، يحدث عزم الجاذبية الصافي على الجسم. عزم الجاذبية هو عزم الدوران الناتج عن الوزن. قد يقوم عزم الجاذبية هذا بتدوير الجسم إذا لم يكن هناك دعم لموازنته. يعتمد حجم عزم الجاذبية على مدى بُعد CM عن المحور. على سبيل المثال، في حالة شاحنة النقل (الشكل\(\PageIndex{2}\))، يقع المحور على الخط الذي تتلامس فيه الإطارات مع سطح الطريق. إذا كان CM مرتفعًا فوق سطح الطريق، فقد يكون عزم الجاذبية كبيرًا بما يكفي لقلب الشاحنة. تعتبر سيارات الركاب ذات السقف المنخفض والقريبة من الرصيف أكثر مقاومة للانقلاب من الشاحنات.
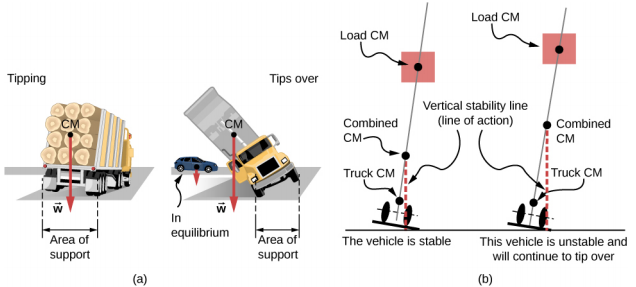
إذا قمت بإمالة مربع بحيث تظل إحدى الحواف على اتصال بالجدول الموجود أسفله، فإن إحدى حواف قاعدة الدعم تصبح محورًا. طالما بقي مركز ثقل الصندوق فوق قاعدة الدعم، يقوم عزم الجاذبية بتدوير الصندوق مرة أخرى نحو موضعه الأصلي للتوازن المستقر. عندما يتحرك مركز الجاذبية خارج قاعدة الدعم، يقوم عزم الجاذبية بتدوير الصندوق في الاتجاه المعاكس، ويتدحرج الصندوق. شاهد هذا العرض التوضيحي لتجربة المواضع المستقرة وغير المستقرة للصندوق.
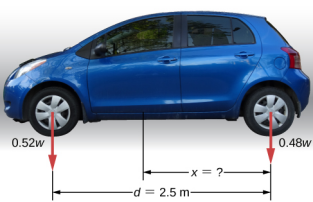
تحتوي سيارة الركاب ذات قاعدة العجلات التي يبلغ طولها 2.5 متر على 52% من وزنها على العجلات الأمامية على الأرض المستوية، كما هو موضح في الشكل 12.4. أين يقع CM لهذه السيارة فيما يتعلق بالمحور الخلفي؟
إستراتيجية
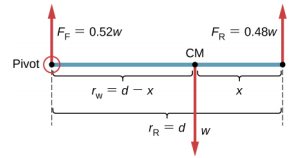
لا نعرف وزن السيارة. كل ما نعرفه هو أنه عندما تستقر السيارة على سطح مستوٍ، تدفع 0.52w لأسفل على السطح عند نقاط التلامس للعجلات الأمامية وتدفع 0.48 واط لأسفل على السطح عند نقاط التلامس للعجلات الخلفية. أيضًا، يتم فصل نقاط الاتصال عن بعضها البعض بالمسافة d = 2.5 متر، وعند نقاط الاتصال هذه، تتعرض السيارة لقوى رد فعل طبيعية بمقادير F = 0.52w و F R = 0.48w على المحاور الأمامية والخلفية، على التوالي. نعلم أيضًا أن السيارة هي مثال لجسم صلب في حالة توازن يعمل وزنه بالكامل w عند CM. يقع CM في مكان ما بين النقاط التي تعمل فيها قوى التفاعل العادية، في مكان ما على مسافة x من النقطة التي تعمل فيها F R. مهمتنا هي إيجاد x، وبالتالي نحدد ثلاث قوى تعمل على الجسم (السيارة)، ويمكننا رسم مخطط الجسم الحر للجسم الصلب الممتد، كما هو موضح في الشكل\(\PageIndex{4}\).
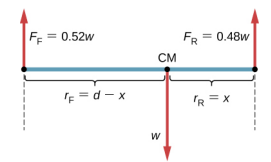
نحن على استعداد تقريبًا لكتابة معادلة شروط التوازن\ ref {12.7} من خلال المعادلة\ ref {12.9} للسيارة، ولكن يجب علينا أولاً تحديد الإطار المرجعي. لنفترض أننا اخترنا المحور السيني بطول السيارة والمحور الصادي والمحور z عموديًا على هذا المستوى السيني. مع هذا الاختيار، نحتاج فقط إلى كتابة المعادلة\ ref {12.7} والمعادلة\ ref {12.9} لأن جميع مكونات y متطابقة في الصفر. الآن نحن بحاجة إلى اتخاذ قرار بشأن موقع النقطة المحورية. يمكننا اختيار أي نقطة كموقع لمحور الدوران (المحور z). لنفترض أننا نضع محور الدوران عند CM، كما هو موضح في مخطط الجسم الحر للسيارة. في هذه المرحلة، نحن على استعداد لكتابة شروط التوازن للسيارة.
الحل
تحتوي كل حالة توازن على ثلاثة مصطلحات فقط لأن هناك قوى N = 3 تعمل على السيارة. تنص حالة التوازن الأولى، المعادلة\ المرجع {12.7}، على ما يلي:
\[+F_{F} - w + F_{R} = 0 \ldotp \label{12.11}\]
يتم استيفاء هذا الشرط بشكل بسيط لأنه عندما نستبدل البيانات، تصبح المعادلة\ المرجع {12.11} +0.52w − w + 0.48w = 0. تنص حالة التوازن الثانية، المعادلة\ المرجع {12.9}، على ما يلي:
\[\tau_{F} + \tau_{w} + \tau_{R} = 0 \label{12.12}\]
أين\(\tau_{F}\) هو عزم القوة F F،\(\tau_{w}\) هو عزم الجاذبية للقوة w،\(\tau_{R}\) وهو عزم القوة F R. عندما يقع المحور عند CM، يكون عزم الجاذبية صفرًا تمامًا لأن ذراع الرافعة للوزن بالنسبة للمحور الذي يمر عبر CM هو صفر. يكون خطي عمل كل من قوتي التفاعل العاديتين متعامدتين على أذرع الرافعة، لذلك في المعادلة\ ref {12.10}، لدينا |sin\(\theta\) | = 1 لكلتا القوتين. من مخطط الجسم الحر، نقرأ أن عزم الدوران\(\tau_{F}\) يسبب دورانًا في اتجاه عقارب الساعة حول المحور عند CM، لذا فإن إحساسه سلبي؛\(\tau_{R}\) ويؤدي عزم الدوران إلى دوران عكس اتجاه عقارب الساعة حول المحور عند CM، لذا فإن إحساسه إيجابي. باستخدام هذه المعلومات، نكتب شرط التوازن الثاني على النحو التالي:
\[-r_{F} F_{F} + r_{R} F_{R} = 0 \ldotp \label{12.13}\]
بمساعدة مخطط الجسم الحر، نحدد مقادير القوة F R = 0.48w و F = 0.52w، وأذرع الرافعة المقابلة لها r = x و r F = d − x. يمكننا الآن كتابة حالة التوازن الثانية، المعادلة\ المرجع {12.13}، بشكل صريح بدلالة مسافة غير معروفة x:
\[-0.52(d - x)w + 0.48xw = 0 \ldotp \label{12.14}\]
هنا يتم إلغاء الوزن w ويمكننا حل معادلة الموضع غير المعروف x لـ CM. الإجابة هي x = 0.52d = 0.52 (2.5 م) = 1.3 متر. الحل اختيار المحور في موضع المحور الأمامي لا يغير النتيجة. يتم عرض مخطط الجسم الحر لهذا الموقع المحوري في الشكل 12.6. بالنسبة لهذا الاختيار للنقطة المحورية، فإن شرط التوازن الثاني هو
\[-r_{w} w + r_{R} F_{R} = 0 \ldotp \label{12.15}\]
عندما نستبدل الكميات المشار إليها في الرسم التخطيطي، نحصل على
\[-(d - x)w + 0.48dw = 0 \ldotp \label{12.16}\]
الإجابة التي تم الحصول عليها عن طريق حل المعادلة\ ref {12.13} هي، مرة أخرى، x = 0.52d = 1.3 م.
الأهمية
يوضح هذا المثال أنه عند حل مشاكل التوازن الثابت، فإننا أحرار في اختيار الموقع المحوري. بالنسبة للاختيارات المختلفة للنقطة المحورية، لدينا مجموعات مختلفة من شروط التوازن لحلها. ومع ذلك، تؤدي جميع الخيارات إلى نفس الحل للمشكلة.
حل المثال 12.1 عن طريق اختيار المحور المحوري في موقع المحور الخلفي.
اشرح أي من الحالات التالية يفي بشرطي الاتزان: (أ) كرة تنس لا تدور أثناء انتقالها في الهواء؛ (ب) طائر البجع الذي ينزلق في الهواء بسرعة ثابتة على ارتفاع واحد؛ أو (ج) العمود المرفقي في محرك سيارة متوقفة.
تحدث حالة خاصة من التوازن الساكن عندما تعمل جميع القوى الخارجية على جسم ما عند محور الدوران أو على طوله أو عندما يمكن تجاهل الامتداد المكاني للكائن. في مثل هذه الحالة، يمكن معالجة الكائن بشكل فعال مثل كتلة نقطية. في هذه الحالة الخاصة، لا داعي للقلق بشأن حالة التوازن الثانية، المعادلة\ ref {12.9}، لأن جميع عزم الدوران متماثل للصفر وشرط التوازن الأول (للقوى) هو الشرط الوحيد الذي يجب الوفاء به. تم توضيح مخطط الجسم الحر واستراتيجية حل المشكلات لهذه الحالة الخاصة في قوانين نيوتن للحركة وتطبيقات قوانين نيوتن. سترى حالة توازن نموذجية تتضمن حالة التوازن الأولى فقط في المثال التالي.
شاهد هذا العرض التوضيحي لرؤية ثلاثة أوزان متصلة بواسطة سلاسل فوق البكرات ومربوطة معًا في عقدة. يمكنك تجربة الأوزان لمعرفة كيفية تأثيرها على موضع توازن العقدة، وفي نفس الوقت، مشاهدة التمثيل التخطيطي المتجهي لحالة التوازن الأولى في العمل.
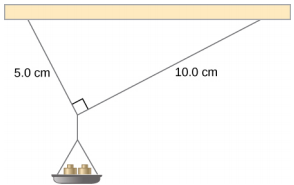
وعاء صغير كتلته 42.0 g مدعوم بسلسلتين، كما هو موضح في الشكل 12.7. الحد الأقصى للشد الذي يمكن أن يدعمه الخيط هو 2.80 نيوتن. تتم إضافة الكتلة تدريجيًا إلى المقلاة حتى تستقر إحدى السلاسل. أي سلسلة هي؟ ما مقدار الكتلة التي يجب إضافتها حتى يحدث ذلك؟
إستراتيجية
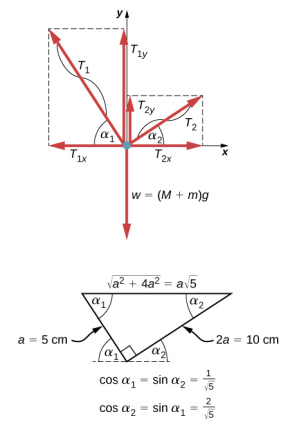
يتكون هذا النظام الميكانيكي من الأوتار والكتل والمقلاة في حالة توازن ثابت. على وجه التحديد، تكون العقدة التي تربط السلاسل بالمقلاة في حالة توازن ثابت. يمكن التعامل مع العقدة كنقطة؛ لذلك، نحتاج فقط إلى حالة التوازن الأولى. القوى الثلاث التي تسحب عند العقدة هي الشد\(\vec{T}_{1}\) في الخيط الذي يبلغ طوله 5.0 سم، والشد\(\vec{T}_{2}\) في الخيط الذي يبلغ طوله 10.0 سم،\(\vec{w}\) ووزن المقلاة التي تحمل الكتل. نعتمد نظام إحداثيات مستطيل مع محور y يشير عكس اتجاه الجاذبية ونرسم مخطط الجسم الحر للعقدة (انظر الشكل 12.8). للعثور على مكونات الشد، يجب أن نحدد زوايا\(\alpha_{1}\) الاتجاه\(\alpha_{2}\) التي تصنعها السلاسل بالاتجاه الأفقي وهو المحور السيني. كما ترى في الشكل 12.7، تشكل السلاسل جانبين للمثلث الأيمن. يمكننا استخدام نظرية فيثاغورس لحل هذا المثلث، الموضح في الشكل 12.8، وإيجاد الجيب وجيب التمام للزوايا\(\alpha_{1}\) و\(\alpha_{2}\). ثم يمكننا حل التوترات في مكوناتها المستطيلة، والاستعاضة في الشرط الأول عن التوازن (المعادلة\ ref {12.7} والمعادلة\ ref {12.8})، وحل التوترات في الأوتار. سوف تنكسر السلسلة ذات التوتر الأكبر أولاً.
الحل
يرجع الوزن الذي يسحب العقدة إلى الكتلة M من المقلاة والكتلة m المضافة إلى المقلاة، أو w = (M + m) g، وبمساعدة مخطط الجسم الحر في الشكل 12.8، يمكننا إعداد شروط التوازن للعقدة:
في الاتجاه السيني،\[-T_{1x} + T_{2x} = 0\] في الاتجاه الصادي،\[+T_{1y} + T_{2y} - w = 0 \ldotp\]
من مخطط الجسم الحر، مقادير المكونات في هذه المعادلات هي
\[\begin{split} T_{1x} & = T_{1} \cos \alpha_{1} = \frac{T_{1}}{\sqrt{5}},\quad T_{1y} = T_{1} \sin \alpha_{1} = \frac{2T_{1}}{\sqrt{5}} \\ T_{2x} & = T_{2} \cos \alpha_{2} = \frac{2T_{2}}{\sqrt{5}},\quad T_{2y} = T_{2} \sin \alpha_{2} = \frac{T_{2}}{\sqrt{5}} \ldotp \end{split}\]
نقوم باستبدال هذه المكونات في ظروف التوازن وتبسيطها. نحصل بعد ذلك على معادلتي توازن للتوترات:
في الاتجاه السيني،\[T_{1} = 2T_{2}\]
في اتجاه y،\[\frac{2T_{1}}{\sqrt{5}} + \frac{T_{2}}{\sqrt{5}} = (M + m)g \ldotp\]
تخبرنا معادلة التوازن للاتجاه x أن الشد T 1 في الخيط الذي يبلغ طوله 5.0 سم يساوي ضعف الشد T 2 في الخيط الذي يبلغ طوله 10.0 سم. لذلك، سيتم قطع السلسلة الأقصر. عندما نستخدم المعادلة الأولى لإزالة T 2 من المعادلة الثانية، نحصل على العلاقة بين الكتلة m على المقلاة والتوتر T 1 في السلسلة الأقصر:
\[\frac{2.5T_{1}}{\sqrt{5}} = (M + m)g \ldotp\]
تنكسر السلسلة عندما يصل التوتر إلى القيمة الحرجة لـ T 1 = 2.80 N. يمكن حل المعادلة السابقة للكتلة الحرجة m التي تكسر السلسلة:
\[m = \frac{2.5}{\sqrt{5}} \frac{T_{1}}{g} - M = \frac{2.5}{\sqrt{5}} \frac{2.80\; N}{9.8\; m/s^{2}} - 0.042\; kg = 0.277\; kg = 277.0\; g \ldotp\]
الأهمية
لنفترض أن النظام الميكانيكي المذكور في هذا المثال متصل بسقف داخل المصعد الصاعد. طالما أن المصعد يتحرك بسرعة ثابتة، تظل النتيجة كما هي لأن الوزن w لا يتغير. إذا تحرك المصعد مع التسارع، تكون الكتلة الحرجة أصغر لأن وزن M + m يصبح أكبر بالوزن الظاهري بسبب تسارع المصعد. ومع ذلك، في جميع الحالات، تنكسر السلسلة الأقصر أولاً.


