11.4: الحفاظ على الزخم الزاوي
- Page ID
- 199893
- قم بتطبيق الحفاظ على الزخم الزاوي لتحديد السرعة الزاوية لنظام الدوران الذي تتغير فيه لحظة القصور الذاتي
- اشرح كيف تتغير طاقة الحركة الدورانية عندما يخضع النظام لتغييرات في كل من لحظة القصور الذاتي والسرعة الزاوية
حتى الآن، نظرنا إلى الزخم الزاوي للأنظمة التي تتكون من الجسيمات النقطية والأجسام الصلبة. لقد قمنا أيضًا بتحليل عزم الدوران المتضمن، باستخدام التعبير الذي يربط عزم الدوران الصافي الخارجي بالتغير في الزخم الزاوي. تتضمن أمثلة الأنظمة التي تخضع لهذه المعادلة إطار دراجة يدور بحرية ويتباطأ بمرور الوقت بسبب عزم الدوران الناتج عن الاحتكاك، أو تباطؤ دوران الأرض على مدى ملايين السنين بسبب قوى الاحتكاك التي تمارس على تشوهات المد والجزر.
ومع ذلك، لنفترض عدم وجود عزم دوران خارجي صافي على النظام،\(\sum \vec{\tau}\) = 0. في هذه الحالة، يمكننا تقديم قانون الحفاظ على الزخم الزاوي.
يتم الحفاظ على الزخم الزاوي لنظام الجسيمات حول نقطة في إطار مرجعي ثابت بالقصور الذاتي إذا لم يكن هناك عزم دوران خارجي صافي حول تلك النقطة:
\[\frac{d \vec{L}}{dt} = 0 \label{11.10}\]
أو
\[\vec{L} = \vec{l}_{1} + \vec{l}_{2} + \cdots + \vec{l}_{N} = constant \ldotp \label{11.11}\]
لاحظ أنه تم الحفاظ على الزخم\(\vec{L}\) الزاوي الكلي. يمكن تغيير أي من اللحظات الزاوية الفردية طالما ظل مجموعها ثابتًا. يماثل هذا القانون الزخم الخطي الذي يتم الحفاظ عليه عندما تكون القوة الخارجية على النظام صفرًا.
وكمثال على الحفاظ على الزخم الزاوي،\(\PageIndex{1}\) يُظهر الشكل متزلجًا على الجليد أثناء الدوران. عزم الدوران الصافي عليها قريب جدًا من الصفر نظرًا لوجود احتكاك قليل نسبيًا بين زلاجاتها والجليد. أيضًا، يتم إجراء الاحتكاك بالقرب جدًا من النقطة المحورية. \(|\vec{r}|\)كلاهما\(|\vec{F}|\) صغير، لذلك لا\(|\vec{\tau}|\) يكاد يذكر. وبالتالي، يمكنها الدوران لبعض الوقت. يمكنها أيضًا زيادة معدل دورانها عن طريق سحب ذراعيها وساقيها. لماذا يزيد سحب ذراعيها وساقيها من معدل دورانها؟ الجواب هو أن زخمها الزاوي ثابت، لذلك
\[L' = L\]
أو
\[I' \omega' = I \omega,\]
حيث تشير الكميات الجاهزة إلى الظروف بعد أن سحبت ذراعيها وقللت من لحظة الجمود. نظرًا لأن I′ أصغر، يجب أن تزداد السرعة\(\omega\) الزاوية للحفاظ على ثبات الزخم الزاوي.
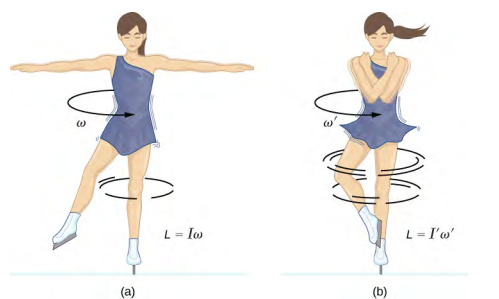
من المثير للاهتمام أن نرى كيف تتغير الطاقة الحركية الدورانية للمتزلجة عندما تسحب ذراعيها إلى الداخل. طاقتها الدورانية الأولية هي
\[K_{Rot} = \frac{1}{2} I \omega^{2},\]
في حين أن طاقتها الدورانية النهائية هي
\[K'_{Rot} = \frac{1}{2} I (\omega')^{2} \ldotp\]
بما أن\(\omega\) I′ ′ = I\(\omega\)، يمكننا أن نستبدل\(\omega\) ′ ونجد
\[K'_{Rot} = \frac{1}{2} I' (\omega')^{2} = \frac{1}{2} I' \left(\dfrac{I}{I'} \omega \right)^{2} = \frac{1}{2} I \omega^{2} \left(\dfrac{I}{I'}\right) = K_{Rot} \left(\dfrac{I}{I'}\right) \ldotp\]
بسبب انخفاض لحظة الجمود\(I′ < I\)، زادت طاقتها الحركية الدورانية النهائية. مصدر هذه الطاقة الحركية الدورانية الإضافية هو العمل المطلوب لسحب ذراعيها إلى الداخل. لاحظ أن أذرع المتزلج لا تتحرك في دائرة مثالية - فهي تدور نحو الداخل. يتسبب هذا العمل في زيادة الطاقة الحركية الدورانية، بينما يظل زخمها الزاوي ثابتًا. نظرًا لأنها في بيئة خالية من الاحتكاك، فلا توجد طاقة تفلت من النظام. وبالتالي، إذا قامت بمد ذراعيها إلى وضعهما الأصليين، فسوف تدور بسرعتها الزاوية الأصلية وستعود طاقتها الحركية إلى قيمتها الأصلية.
النظام الشمسي هو مثال آخر على كيفية عمل الحفاظ على الزخم الزاوي في عالمنا. وُلد نظامنا الشمسي من سحابة ضخمة من الغاز والغبار كانت تحتوي في البداية على طاقة دورانية. تسببت قوى الجاذبية في تقلص السحابة، وزاد معدل الدوران نتيجة الحفاظ على الزخم الزاوي (الشكل\(\PageIndex{2}\)).
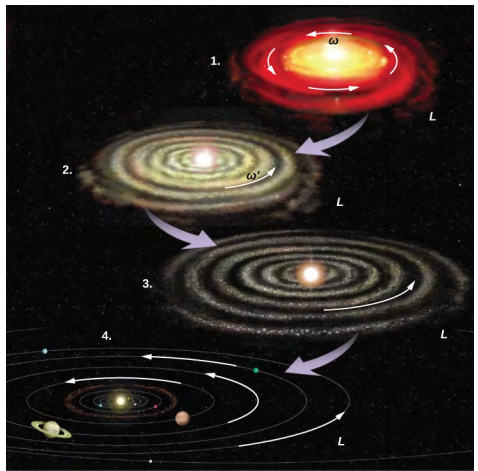
نواصل مناقشتنا بمثال له تطبيقات في الهندسة.
تدور دولاب الموازنة بدون احتكاك بسرعة زاوية\(\omega_{0}\) = 600 لفة/دقيقة على عمود عمودي غير احتكاكي ذي قصور دوراني ضئيل. يتم إسقاط دولاب الموازنة الثاني، الذي يكون في حالة سكون ولديه لحظة من القصور الذاتي ثلاث مرات من دولاب الموازنة الدوارة، عليها (الشكل\(\PageIndex{3}\)). نظرًا لوجود احتكاك بين الأسطح، تصل الحذافات بسرعة كبيرة إلى نفس سرعة الدوران، وبعد ذلك تدور معًا.
- استخدم قانون الحفاظ على الزخم الزاوي لتحديد السرعة\(\omega\) الزاوية للمجموعة.
- ما الكسر من طاقة الحركة الأولية المفقودة في اقتران الحذافات؟
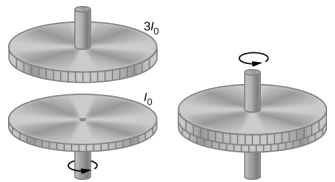
إستراتيجية
الجزء (أ) سهل الحل للسرعة الزاوية للنظام المزدوج. نستخدم نتيجة (أ) لمقارنة الطاقات الحركية الأولية والنهائية للنظام في الجزء (ب).
الحل
- لا توجد عزم دوران خارجي يعمل على النظام. تنتج القوة الناتجة عن الاحتكاك عزم دوران داخلي لا يؤثر على الزخم الزاوي للنظام. لذلك فإن الحفاظ على الزخم الزاوي يعطي\[I_{0} \omega_{0} = (I_{0} + 3I_{0}) \omega, \nonumber\]\[\omega = \frac{1}{4} \omega_{0} = 150\; rev/min = 15.7\; rad/s \ldotp \nonumber\]
- قبل الاتصال، يتم تدوير دولاب الموازنة واحد فقط. الطاقة الحركية الدورانية لعجلة الموازنة هذه هي الطاقة الحركية الدورانية الأولية للنظام\(\frac{1}{2} I_{0} \omega_{0}^{2}\). الطاقة الحركية النهائية هي\[\frac{1}{2} (4I_{0}) \omega^{2} = \frac{1}{2} (4I_{0}) \left(\dfrac{\omega_{0}}{4}\right)^{2} = \frac{1}{8} I_{0} \omega_{0}^{2}. \nonumber\] لذلك، فإن نسبة الطاقة الحركية النهائية إلى الطاقة الحركية الأولية هي،\[\frac{\frac{1}{8} I_{0} \omega_{0}^{2}}{\frac{1}{2} I_{0} \omega_{0}^{2}} = \frac{1}{4} \ldotp \nonumber\] وبالتالي، يتم فقدان 3/4 من الطاقة الحركية الأولية بسبب اقتران الحذافتين.
الأهمية
منذ زيادة القصور الدوراني للنظام، انخفضت السرعة الزاوية، كما هو متوقع من قانون الحفاظ على الزخم الزاوي. في هذا المثال، نرى أن الطاقة الحركية النهائية للنظام قد انخفضت، حيث يتم فقدان الطاقة بسبب اقتران الحذافات. قارن هذا بمثال المتزلجة في الشكل وهي\(\PageIndex{1}\) تقوم بعمل لجلب ذراعيها إلى الداخل وإضافة طاقة حركية دورانية.
تدور جولة المرح في الملعب بمعدل 4.0 لفة/دقيقة. يقفز ثلاثة أطفال ويزيدون من لحظة القصور الذاتي لنظام المرح والدوران للأطفال بنسبة 25٪. ما هو معدل الدوران الجديد؟
ترحل لاعبة جمباز تزن 80.0 كجم من حانة عالية. يبدأ الترجل بالامتداد الكامل، ثم يقوم بالثنيات لإكمال عدد من الثورات قبل الهبوط. يمكن تقريب لحظة القصور الذاتي عند تمديده بالكامل كقضيب طوله 1.8 متر وعندما يكون في الثنية قضيب بنصف هذا الطول. إذا كان معدل دورانه عند الامتداد الكامل ١٫٠ لفة/ثانية ودخل الثنية عندما يكون مركز كتلته على ارتفاع ٣٫٠ م متحركًا أفقيًا نحو الأرض، فما عدد الثورات التي يمكنه تنفيذها إذا خرج من الثنية بارتفاع ١٫٨ م؟ انظر الشكل\(\PageIndex{4}\).
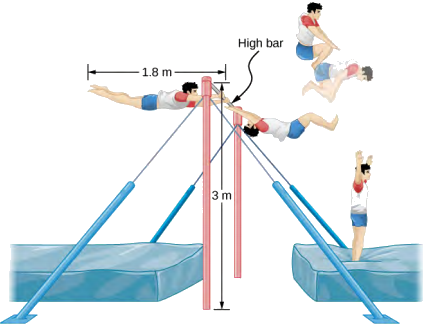
إستراتيجية
باستخدام الحفاظ على الزخم الزاوي، يمكننا إيجاد معدل دورانه عندما يكون في الثنية. باستخدام معادلات الكينماتيكا، يمكننا إيجاد الفاصل الزمني من ارتفاع ٣٫٠ م إلى ١٫٨ م، ونظرًا لأنه يتحرَّك أفقيًّا بالنسبة إلى الأرض، تُبسِّط معادلات السقوط الحر. سيسمح هذا بحساب عدد الثورات التي يمكن تنفيذها. نظرًا لأننا نستخدم النسبة، يمكننا الاحتفاظ بالوحدات على هيئة rev/s ولا نحتاج إلى التحويل إلى radians/s.
الحل
لحظة الجمود عند الامتداد الكامل هي\[I_{0} = \frac{1}{12} mL^{2} = \frac{1}{12} (80.0\; kg)(1.8\; m)^{2} = 21.6\; kg\; \cdotp m^{2} \ldotp \nonumber\]
لحظة القصور الذاتي في الثنية هي\[I_{f} = \frac{1}{12} mL_{f}^{2} = \frac{1}{12} (80.0\; kg)(0.9\; m)^{2} = 5.4\; kg\; \cdotp m^{2} \ldotp \nonumber\]
الحفاظ على الزخم الزاوي:\[I_{f} \omega_{f} = I_{0} \omega_{0} \Rightarrow \omega_{f} = \frac{I_{0} \omega_{0}}{I_{f}} = \frac{(21.6\; kg\; \cdotp m^{2})(1.0\; rev/s)}{5.4\; kg\; \cdotp m^{2}} = 4.0\; rev/s \ldotp \nonumber\]
الفاصل الزمني في الثنية:\[t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2(3.0 - 1.8) m}{9.8\; m/s}} = 0.5\; s \ldotp \nonumber\]
في غضون 0.5 ثانية، سيكون قادرًا على تنفيذ دورتين بسرعة 4.0 لفة/ثانية.
الأهمية
لاحظ أن عدد الثورات التي يمكنه إكمالها سيعتمد على مدة وجوده في الهواء. في المشكلة، يخرج من الشريط العالي أفقيًا على الأرض. يمكنه أيضًا الخروج بزاوية فيما يتعلق بالأرض، مما يمنحه وقتًا أطول أو أقل في الهواء اعتمادًا على الزاوية، الإيجابية أو السلبية، فيما يتعلق بالأرض. يجب على لاعبي الجمباز أخذ ذلك في الاعتبار عند تنفيذ التخفيضات الخاصة بهم.
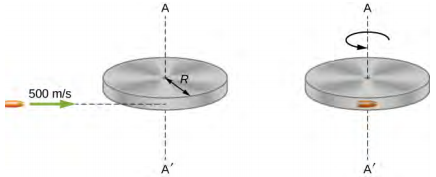
تتحرَّك رصاصة كتلتها m = 2.0 g أفقيًّا بسرعة 500.0 م/ث، وتسقط الرصاصة في حافة قرص صلب كتلته M = 3.2 kg ونصف قطر R = 0.5 m، وتكون الأسطوانة حرة في الدوران حول محورها وتكون في وضع السكون مبدئيًا (الشكل\(\PageIndex{5}\)). ما السرعة الزاوية للقرص مباشرة بعد دمج الرصاصة؟
إستراتيجية
بالنسبة لنظام الرصاصة والأسطوانة، لا يعمل أي عزم دوران خارجي على طول المحور الرأسي من خلال مركز القرص. وبالتالي، يتم الحفاظ على الزخم الزاوي على طول هذا المحور. والزخم الزاوي الأولي للرصاصة هو mVR، والذي يتم التقاطه حول المحور الدوراني للقرص في اللحظة التي تسبق التصادم. الزخم الزاوي الأولي للأسطوانة هو صفر. وبالتالي، فإن الزخم الزاوي الصافي للنظام هو mVR. نظرًا للحفاظ على الزخم الزاوي، فإن الزخم الزاوي الأولي للنظام يساوي الزخم الزاوي للرصاصة المضمنة في القرص مباشرة بعد الاصطدام.
الحل
الزخم الزاوي الأولي للنظام هو
\[L_{i} = mvR \ldotp \nonumber\]
لحظة القصور الذاتي للنظام مع الرصاصة المضمنة في القرص هي
\[I = mR^{2} + \frac{1}{2} MR^{2} = \left(m + \dfrac{M}{2}\right) R^{2} \ldotp \nonumber\]
الزخم الزاوي النهائي للنظام هو
\[L_{f} = I \omega_{f} \ldotp \nonumber\]
وهكذا، من خلال الحفاظ على الزخم الزاوي، L i = L f و
\[mvR = \left(m + \dfrac{M}{2}\right) R^{2} \omega_{f} \ldotp \nonumber\]
حل لـ\(\omega_{f}\)،
\[\omega_{f} = \frac{mvR}{\left(m + \dfrac{M}{2}\right) R^{2}} = \frac{(2.0 \times 10^{-3}\; kg)(500.0\; m/s)}{(2.0 \times 10^{-3}\; kg + 1.6\; kg)(0.50\; m)} = 1.2\; rad/s \ldotp \nonumber\]
الأهمية
يتكون النظام من جسيم نقطي وجسم صلب. يجب توخي الحذر عند صياغة الزخم الزاوي قبل التصادم وبعده. قبل التأثير مباشرة، يتم أخذ الزخم الزاوي للرصاصة حول المحور الدوراني للقرص.


