11.3: الزخم الزاوي

أهداف التعلم

• وصف الطبيعة المتجهة للزخم الزاوي
• أوجد إجمالي الزخم الزاوي وعزم الدوران حول أصل معين لنظام الجسيمات
• احسب كمية الحركة الزاوية لجسم صلب يدور حول محور ثابت
• احسب عزم الدوران على جسم صلب يدور حول محور ثابت
• استخدم الحفاظ على الزخم الزاوي في تحليل الكائنات التي تغير معدل دورانها

لماذا تستمر الأرض في الدوران؟ ما الذي بدأ الدوران في البداية؟ لماذا لا تؤدي جاذبية الأرض إلى سقوط القمر نحو الأرض؟ وكيف تتمكن المتزلجة على الجليد من الدوران بشكل أسرع وأسرع ببساطة عن طريق سحب ذراعيها للداخل؟ لماذا لا تضطر إلى ممارسة عزم الدوران بشكل أسرع؟

الإجابة على هذه الأسئلة هي أنه مثلما يتم الحفاظ على الحركة الخطية الكلية (الزخم) في الكون، يتم الحفاظ على الحركة الدورانية الكلية. نسمي الزخم الزاوي للحركة الدورانية الكلية، النظير الدوراني للزخم الخطي. في هذا الفصل، نحدد أولاً ثم نستكشف الزخم الزاوي من مجموعة متنوعة من وجهات النظر. ومع ذلك، أولاً، نبحث في الزخم الزاوي لجسيم واحد. هذا يسمح لنا بتطوير الزخم الزاوي لنظام الجسيمات والجسم الصلب.

كمية الحركة الزاوية لجسيم واحد

\(\PageIndex{1}\)يوضِّح الشكل جسيمًا في موضع\(\vec{r}\) ذي زخم خطي\(\vec{p}\) = m\(\vec{v}\) بالنسبة إلى الأصل. حتى إذا كان الجسيم لا يدور حول الأصل، فلا يزال بإمكاننا تحديد الزخم الزاوي من حيث متجه الموضع والزخم الخطي.

كمية الحركة الزاويّة للجسيم

يُعرَّف الزخم\(\vec{l}\) الزاوي للجسيم بأنه الناتج المتقاطع لـ\(\vec{r}\) and\(\vec{p}\)، وهو عمودي على المستوى الذي يحتوي على\(\vec{r}\) و\(\vec{p}\):

\[\vec{l} = \vec{r} \times \vec{p} \ldotp \label{11.5}\]

الشكل\(\PageIndex{1}\): في الفضاء ثلاثي الأبعاد،\(\vec{r}\) يحدد متجه الموضع جسيمًا في المستوى السيني بزخم خطي\(\vec{p}\). الزخم الزاوي فيما يتعلق بالأصل هو\(\vec{l} = \vec{r} \times \vec{p}\)، الذي يقع في الاتجاه z. \(\vec{l}\)يتم تحديد الاتجاه من خلال قاعدة اليد اليمنى، كما هو موضح.

الهدف من اختيار اتجاه الزخم الزاوي ليكون عموديًا على المستوى الذي يحتوي على\(\vec{r}\)\(\vec{p}\) ويشبه اختيار اتجاه عزم الدوران ليكون عموديًا على مستوى\(\vec{r}\) و\(\vec{F}\)، كما تمت مناقشته في دوران المحور الثابت. تم العثور على حجم الزخم الزاوي من تعريف المنتج المتقاطع،

\[l = rp \sin \theta,\]

\(\theta\)أين الزاوية بين\(\vec{r}\) و\(\vec{p}\). وحدات الزخم الزاوي هي kg • m ² ss. كما هو الحال مع تعريف عزم الدوران، يمكننا تحديد ذراع الرافعة\(r_\perp\) الذي يمثل المسافة العمودية من متجه الزخم\(\vec{p}\) إلى الأصل،\(r_\perp = r \sin \theta\). مع هذا التعريف، يصبح حجم الزخم الزاوي

\[l = r_{\perp} p = r_{\perp} mv \ldotp\]

نرى أنه إذا كان الاتجاه بحيث\(\vec{p}\) يمر عبر نقطة الأصل، فعندئذٍ\(\theta\) = 0، والزخم الزاوي هو صفر لأن ذراع الرافعة صفر. في هذا الصدد، يعتمد حجم الزخم الزاوي على اختيار الأصل. إذا أخذنا المشتق الزمني للزخم الزاوي، نصل إلى تعبير عن عزم الدوران على الجسيم:

\[ \begin{align*} \frac{d \vec{l}}{dt} &= \frac{d \vec{r}}{dt} \times \vec{p} + \vec{r} \times \frac{d \vec{p}}{dt} \\[4pt] &= \vec{v} \times m \vec{v} + \vec{r} \times \frac{d \vec{p}}{dt} \\[4pt] &= \vec{r} \times \frac{d \vec{p}}{dt} \ldotp \end{align*}\]

لقد استخدمنا هنا التعريف وحقيقة أن المتجه الذي تم عبوره إلى نفسه هو صفر.\(\vec{p}\) من قانون نيوتن الثاني\(\frac{d \vec{p}}{dt} = \sum \vec{F}\)، والقوة الكلية المؤثرة على الجسيم، وتعريف عزم الدوران الصافي، يمكننا أن نكتب

\[\frac{d \vec{l}}{dt} = \sum \vec{\tau} \ldotp \label{11.6}\]

لاحظ التشابه مع النتيجة الخطية لقانون نيوتن الثاني،\(\frac{d \vec{p}}{dt} = \sum \vec{F}\). يمكن أن تكون استراتيجية حل المشكلات التالية بمثابة دليل لحساب الزخم الزاوي للجسيم.

إستراتيجية حل المشكلات: الزخم الزاوي للجسيم

1. اختر نظام الإحداثيات الذي سيتم حساب الزخم الزاوي حوله.
2. اكتب متجه نصف القطر إلى الجسيم النقطي في رمز متجه الوحدة.
3. اكتب متجه الزخم الخطي للجسيم في رمز متجه الوحدة.
4. خذ المنتج المتقاطع\(\vec{l} = \vec{r} \times \vec{p}\) واستخدم القاعدة اليمنى لتحديد اتجاه متجه الزخم الزاوي.
5. تحقق مما إذا كان هناك اعتماد زمني في التعبير عن متجه الزخم الزاوي. إذا كان هناك، فسيكون هناك عزم دوران حول الأصل، ويستخدم\(\frac{d \vec{l}}{dt} = \sum \vec{\tau}\) لحساب عزم الدوران. إذا لم يكن هناك اعتماد زمني في التعبير عن الزخم الزاوي، فإن عزم الدوران الصافي يكون صفرًا.

مثال\(\PageIndex{2}\): Angular Momentum and Torque on a Meteor

يدخل نيزك الغلاف الجوي للأرض (الشكل\(\PageIndex{2}\)) ويراقبه شخص ما على الأرض قبل أن يحترق في الغلاف الجوي. \(\hat{j}\)يعطي المتجه\(\vec{r}\) = 25 كم\(\hat{i}\) + 25 كم موضع النيزك بالنسبة للراصد. في اللحظة التي يرى فيها الراصد النيزك، يكون له زخم خطي\(\vec{p}\) = (15.0 كجم) (−2.0 كم/ثانية\(\hat{j}\))، ويتسارع بسرعة ثابتة تبلغ 2.0 م/ث ² (\(− \hat{j}\)) على طول مساره، وهو ما يمكن اعتباره لأغراضنا كخط مستقيم.

1. ما مقدار الحركة الزاوية للنيزك حول نقطة الأصل، التي تقع في موقع الراصد؟
2. ما عزم دوران النيزك حول نقطة الأصل؟

الشكل\(\PageIndex{2}\): يرى مراقب على الأرض نيزكًا في موضعه\(\vec{r}\) بقوة دفع خطية\(\vec{p}\).

إستراتيجية

نقوم بحل التسارع إلى مكونات x- و y ونستخدم المعادلات الحركية للتعبير عن السرعة كدالة للتسارع والوقت. نقوم بإدخال هذه التعبيرات في الزخم الخطي ثم نحسب الزخم الزاوي باستخدام المنتج المتقاطع. نظرًا لوجود متجهات الموضع والزخم في المستوى السيني، نتوقع أن يكون متجه الزخم الزاوي على طول المحور z. لإيجاد عزم الدوران، نأخذ المشتق الزمني للزخم الزاوي.

الحل

يدخل النيزك الغلاف الجوي للأرض بزاوية 90.0 درجة تحت الأفقي، وبالتالي فإن مكونات التسارع في الاتجاهين x- و y هي

\[a_{x} = 0,\; a_{y} = -2.0\; m/s^{2} \ldotp \nonumber\]

نكتب السرعات باستخدام المعادلات الحركية.

\[v_{x} = 0,\; v_{y} = (-2.0 \times 10^{3}\; m/s) - (2.0\; m/s^{2})t \ldotp \nonumber\]

1. الزخم الزاوي هو\[\begin{split} \vec{l} & = \vec{r} \times \vec{p} = (25.0\; km\; \hat{i} + 25.0\; km\; \hat{j}) \times (15.0\; kg)(0 \hat{i} + v_{y} \hat{j}) \\ & = 15.0\; kg [ 25.0\; km (v_{y}) \hat{k}] \\ & = 15.0\; kg \{ (2.50 \times 10^{4}\; m)[(-2.0 \times 10^{3}\; m/s) - (2.0\; m/s^{2})t] \hat{k} \} \ldotp \end{split} \nonumber\] At = 0، والزخم الزاوي للنيزك حول الأصل هو\[\vec{l}_{0} = 15.0\; kg [ (2.50 \times 10^{4}\; m)(-2.0 \times 10^{3}\; m/s) \hat{k}] = 7.50 \times 10^{8}\; kg\; \cdotp m^{2}/s (- \hat{k}) \ldotp \nonumber\] هذه هي اللحظة التي يرى فيها الراصد النيزك.
2. لإيجاد عزم الدوران، نأخذ المشتق الزمني للزخم الزاوي. بأخذ المشتق الزمني\(\vec{l}\) كدالة للوقت، وهي المعادلة الثانية أعلاه مباشرة، لدينا\[\frac{d \vec{l}}{dt} = (-15.0\; kg)(2.50 \times 10^{4}\; m)(2.0\; m/s^{2}) \hat{k} \ldotp \nonumber\] بعد ذلك، ومنذ ذلك الحين\(\frac{d \vec{l}}{dt} = \sum \vec{\tau}\)، وحدات عزم الدوران تُعطى في صورة نيوتن متر، ولا ينبغي الخلط بينها وبين الجول.\[\sum \vec{\tau} = -7.5 \times 10^{5}\; N\; \cdotp m\; \hat{k} \ldotp \nonumber\] وكفحص، نلاحظ أن ذراع الرافعة هو المكون x للمتجه\(\vec{r}\) في الشكل\(\PageIndex{2}\) لأنه عمودي على القوة المؤثرة على النيزك، الذي يقع على طول مساره. بموجب قانون نيوتن الثاني، هذه القوة هي $$\ vec {F} = MA (-\ hat {j}) = (15.0\؛ كجم) (2.0\؛ م/s^ {2}) (-\ قبعة {j}) = 30.0\؛ كجم\؛\ cdotp m/s^ {2} (-\ قبعة {j})\ lDotp $) ذراع الرافعة هو $\ vec} _ {\ perp} = 2.5\ مرات 10^ {4}\; م\;\ قبعة {i}\ ldoTP$$وبالتالي، فإن عزم الدوران هو $$\ ابدأ {الانقسام}\ المجموع\ vec {\ tau} =\ vec {r} _ {\ perp}\ مرات\ vec {\ perp}\ مرات\ vec {\ F } & = (2.5\ مرات 10^ {4}\؛ م\؛\ قبعة {i})\ مرات (-30.0\؛ كجم\؛\ cdotp m/s^ {2}\؛\\ قبعة {j})،\\\ & = 7.5\ مرات 10^ {5\\؛ N\\ cdotp m (-\ hat {k})\ ldotp\ End slit {j} $$

الأهمية

نظرًا لأن النيزك يتسارع نحو الأرض، يتغير نصف قطره ومتجه السرعة. لذلك\(\vec{l} = \vec{r} \times \vec{p}\)، نظرًا لأن الزخم الزاوي يتغير كدالة للوقت. ومع ذلك، فإن عزم النيزك حول الأصل ثابت، لأن ذراع الرافعة\(\vec{r}_{\perp}\) والقوة على النيزك ثوابت. هذا المثال مهم لأنه يوضح أن الزخم الزاوي يعتمد على اختيار الأصل الذي يتم حسابه به. تعتبر الطرق المستخدمة في هذا المثال مهمة أيضًا في تطوير الزخم الزاوي لنظام الجسيمات والجسم الصلب.

التمارين الرياضية\(\PageIndex{1}\)

يقوم بروتون يدور حول مجال مغناطيسي بتنفيذ حركة دائرية في مستوى الورقة، كما هو موضح أدناه. نصف قطر المسار الدائري ٠٫٤ م، وسرعة البروتون ٤٫٠ × ١٠ ^٦ م/ث، ما مقدار الحركة الزاوية للبروتون حول نقطة الأصل؟

الزخم الزاوي لنظام الجسيمات

إن الزخم الزاوي لنظام الجسيمات مهم في العديد من التخصصات العلمية، وأحدها علم الفلك. تأمل المجرة الحلزونية، جزيرة دوارة من النجوم مثل درب التبانة الخاص بنا. يمكن التعامل مع النجوم الفردية كجسيمات نقطية، ولكل منها زخمها الزاوي الخاص. يعطي المجموع المتجه للحظات الزاوية الفردية الزخم الزاوي الكلي للمجرة. في هذا القسم، نقوم بتطوير الأدوات التي يمكننا من خلالها حساب الزخم الزاوي الكلي لنظام الجسيمات.

في القسم السابق، قدمنا الزخم الزاوي لجسيم واحد حول أصل معين. التعبير عن هذا الزخم الزاوي هو\(\vec{l} = \vec{r} \times \vec{p}\)، حيث\(\vec{r}\) يكون المتجه من الأصل إلى الجسيم،\(\vec{p}\) وهو الزخم الخطي للجسيم. إذا كان لدينا نظام من جسيمات N، ولكل منها متجه موضعي من نقطة الأصل المعطاة\(\vec{r}_{i}\) ولكل منها زخم\(\vec{p}_{i}\)، فإن الزخم الزاوي الكلي لنظام الجسيمات حول الأصل هو المجموع المتجه للحظات الزاوية الفردية حول الأصل. وهذا هو،

\[\vec{L} = \vec{l}_{1} + \vec{l}_{2} + \cdots + \vec{l}_{N} \ldotp \label{11.7}\]

وبالمثل، إذا كان الجسيم i خاضعًا لعزم دوران صافٍ\(\vec{\tau_{i}}\) حول الأصل، فيمكننا إيجاد عزم الدوران الصافي حول الأصل بسبب نظام الجسيمات عن طريق التفريق بين المعادلة 11.7:

\[\frac{d \vec{L}}{dt} = \sum_{i} \frac{d \vec{l}_{i}}{dt} = \sum_{i} \tau_{i} \ldotp\]

ينتج مجموع عزم الدوران الفردي عزم دوران خارجي صافيًا على النظام الذي نحدده\(\sum \vec{\tau}\). وهكذا،

\[\frac{d \vec{L}}{dt} = \sum_{i} \tau_{i} \ldotp \label{11.8}\]

تنص المعادلة\ ref {11.8} على أن معدل التغيير في الزخم الزاوي الكلي للنظام يساوي صافي عزم الدوران الخارجي الذي يعمل على النظام عندما يتم قياس كلتا الكميتين فيما يتعلق بأصل معين. يمكن تطبيق المعادلة\ ref {11.8} على أي نظام يحتوي على الزخم الزاوي الصافي، بما في ذلك الأجسام الصلبة، كما هو موضح في القسم التالي.

مثال\(\PageIndex{2}\): Angular Momentum of Three Particles

بالإشارة إلى الشكل\(\PageIndex{1a}\):

1. أوجد الزخم الزاوي الكلي الناتج عن الجسيمات الثلاثة حول الأصل.
2. ما معدَّل تغيُّر الزخم الزاوي؟

الشكل\(\PageIndex{3}\): ثلاثة جسيمات في المستوى السيني بموضع مختلف ومتجهات زخم مختلفة.

إستراتيجية

اكتب الموضع ومتجهات الزخم للجسيمات الثلاثة. احسب اللحظات الزاوية الفردية وأضفها كمتجهات للعثور على الزخم الزاوي الكلي. ثم افعل نفس الشيء بالنسبة لعزم الدوران.

الحل

1. الجسيم 1: $$\ vec {r} _ {1} = -2.0\؛ م\؛\ قبعة {i} + 1.0\؛ م\؛\ قبعة {j}،\\\\\\ vec {p} _ {1} = (2.0\؛ كجم) (4.0\؛ م/ث\؛\ قبعة {j}) = 8.0\؛ كغ\؛\ cdotp m/s\؛\\ قبعة {j}، $$\ vec {l} _ {1} =\ vec {r} _ {1}\ مرات\ فيك {p} _ {1} = -16.0\؛ كجم\؛\ cdotp m^ {2} /s\؛\ قبعة {k}\ ldotp$$ الجسيمات 2: $$\ vec {r} _ {2} = 4.0\؛ م\؛\\ قبعة {j},\;\ vec {p} _ {2} = (4.0\; كجم) (5.0\; م/ث\;\ قبعة {i}) = 20.0\; كجم\;\ cdotp m/s\;\ قبعة {i}, $$$$$\ vec {l} _ {2} =\ vec {r} _ {2} =\ vec {r} _ {2} =\ vec {r} _ {2} =\ vec {r} _ {2} =\ vec {r} _ {2}; kg\;\ cdotp m^ {2} /s\;\ قبعة {k}\ lDOTP$الجسيم 3: $\ vec {r} _ {3} = 2.0\; م\;\ قبعة {i} - 2.0\; م\;\ قبعة {j},\\ hat {j},\\\\ vec {p} _ {3} = (1.0\; كغ) (3.0\; م/ث\;\\ قبعة} {i}) = 3.0\؛ كجم\؛ \ cdotp m/s\;\ hat {j}, $$ $\ vec {l} _ {3} =\ vec {r} _ {3}\ مرات\ فيك {p} _ {3} = 6.0\; كجم\;\ cdotp m^ {2} /s\;\ hat {k}\ lDotp $نضيف اللحظات الزاويّة الفردية للعثور على المجموع حول الأصل: $$\ vec {l} _ {T} =\ vec {l} _ {1} +\ vec {l} _ {2} +\ vec {l} _ {3} = -30\؛ كجم\؛\ cdotp m^ {2} /s\؛\ قبعة {ك}\ ldotp $$
2. القوات الفردية وأذرع الرافعة هي $$\ begin {split}\ vec {r} _ {1\ perp} & = 1.0\؛\\\ قبعة {j}،\\\ قبعة {j}،\\\\\\\\\ قبعة {j} _ {1} = 6.0\؛\\\\\\\\\\\\\\\}\\\ vec {r} _ {2\ perp} & = 4.0\؛ م\؛\ قبعة {i}،\؛\ vec {F} _ {2} = 10.0\؛ N\؛\\ قبعة {i}،\؛\ vec {\ تاو} _ {2} = 40.0\؛ N\؛\ cdotp\؛\ قبعة {k}\\\ vec {r} _ {3\ perp} & = 2.0\؛ م\؛\ قبعة {j}،\\\\\\ vec {F} _ {3} = -8.0\؛ N\؛\ قبعة {j}\؛\\\ vec {\ تاو} _ {3} = -16.0\؛ N\ cdotp\؛\\ قبعة {k}\ ldotp\ النهاية {الانقسام} $$لذلك: $$\ sum_ {i}\ vec {\ تاو} _ {i} =\ فيك {\ تاو} _ {1} +\ فيك {2} +\ فيك {\ تاو} _ {\ تاو} _ {3} = 30\; N\;\ cdotp m\;\ قبعة {k}\ ldotp $$

الأهمية

يوضح هذا المثال مبدأ التراكب للزخم الزاوي وعزم الدوران لنظام الجسيمات. يجب توخي الحذر عند تقييم متجهات\(\vec{r}_{i}\) نصف قطر الجسيمات لحساب اللحظات الزاوية وأذرع الرافعة\(\vec{r}_{i \perp}\) لحساب عزم الدوران، لأنها كميات مختلفة تمامًا.

الزخم الزاوي لجسم جاسئ

لقد بحثنا في الزخم الزاوي لجسيم واحد، والذي قمنا بتعميمه على نظام من الجسيمات. الآن يمكننا استخدام المبادئ التي تمت مناقشتها في القسم السابق لتطوير مفهوم الزخم الزاوي للجسم الصلب. تتمتع الأجسام السماوية مثل الكواكب بزخم زاوي بسبب دورانها ومداراتها حول النجوم. في مجال الهندسة، يحمل أي شيء يدور حول محور زخمًا زاويًا، مثل الحذافات والمراوح والأجزاء الدوارة في المحركات. تعد معرفة اللحظات الزاوية لهذه الكائنات أمرًا بالغ الأهمية لتصميم النظام الذي تشكل جزءًا منه.

لتطوير الزخم الزاوي للجسم الصلب، نقوم بنمذجة الجسم الصلب على أنه يتكون من أجزاء كتلة صغيرة،\(\Delta\) m _i. في الشكل\(\PageIndex{4}\)، يتم تقييد الجسم الصلب للدوران حول المحور z بسرعة زاوية\(\omega\). تخضع جميع مقاطع الكتلة التي يتكون منها الجسم الصلب لحركة دائرية حول المحور z بنفس السرعة الزاوية. يُظهر الجزء (أ) من الشكل مقطع الكتلة\(\Delta\) m _i مع متجه الموضع\(\vec{r}_{i}\) من نقطة الأصل ونصف القطر R _i إلى المحور z. حجم سرعته العرضية هو v _i = R _i\(\omega\). نظرًا لأن المتجهين\(\vec{v}_{i}\)\(\vec{r}_{i}\) متعامدتان مع بعضهما البعض، فإن مقدار الزخم الزاوي لهذا الجزء الكتلي هو

\[l_{i} = r_{i} (\Delta mv_{i}) \sin 90^{o} \ldotp\]

الشكل\(\PageIndex{4}\): (أ) الجسم الصلب مقيد بالدوران حول المحور z. الجسم الصلب متماثل حول المحور z. يقع مقطع الكتلة\(\Delta\) m _i في الموضع\(\vec{r}_{i}\)، مما يجعل الزاوية\(\theta_{i}\) بالنسبة للمحور z. تظهر الحركة الدائرية لمقطع الكتلة المتناهية الصغر. (ب)\(\vec{l}_{i}\) هو الزخم الزاوي للجزء الكتلي وله مكون على طول المحور z (\(\vec{l}_{i}\)) _z.

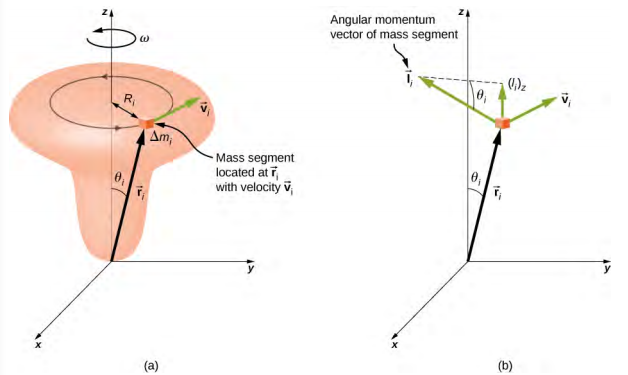
باستخدام قاعدة اليد اليمنى، يشير متجه الزخم الزاوي في الاتجاه الموضح في الشكل\(\PageIndex{4b}\). يحتوي مجموع اللحظات الزاوية لجميع مقاطع الكتلة على مكونات بطول محور الدوران وعموديًا عليه. يحتوي كل مقطع كتلي على مكون عمودي من الزخم الزاوي الذي سيتم إلغاؤه بواسطة المكون العمودي لقطعة كتلة متطابقة على الجانب الآخر من الجسم الصلب. وبالتالي، فإن المكون على طول محور الدوران هو المكون الوحيد الذي يعطي قيمة غير صفرية عند جمعها على جميع مقاطع الكتلة. من الجزء (ب)، يكون المكون الموجود\(\vec{l}_{i}\) على طول محور الدوران هو

\[\begin{split} (l_{i})_{z} & = l_{i} \sin \theta_{i} = (r_{i} \Delta m_{i} v_{i}) \sin \theta_{i}, \\ & = (r_{i} \sin \theta_{i})(\Delta m_{i} v_{i}) = R_{i} \Delta m_{i} v_{i} \ldotp \end{split}\]

الزخم الزاوي الصافي للجسم الصلب على طول محور الدوران هو

\[L = \sum_{i} (\vec{l}_{i})_{z} = \sum_{i} R_{i} \Delta m_{i} v_{i} = \sum_{i} R_{i} \Delta m_{i} (R_{i} \omega) = \omega \sum_{i} \Delta m_{i} (R_{i})^{2} \ldotp\]

إن التلخيص\(\sum_{i} \Delta\) (R _i) ² هو ببساطة لحظة القصور الذاتي الأول للجسم الصلب حول محور الدوران. بالنسبة إلى الطوق الرقيق الذي يدور حول محور عمودي على مستوى الطوق، فإن كل حرف R _i يساوي R وبالتالي ينخفض المجموع إلى R ²\(\sum_{i} \Delta\) m _i = mR ²، وهي لحظة القصور الذاتي للطوق الرقيق الموجود في الشكل 10.20. وبالتالي، فإن حجم الزخم الزاوي على طول محور دوران جسم صلب يدور بسرعة زاوية\(\omega\) حول المحور هو

\[L = I \omega \ldotp \label{11.9}\]

هذه المعادلة مماثلة لحجم الزخم الخطي p = mv. يتم توجيه اتجاه متجه الزخم الزاوي على طول محور الدوران المعطى بقاعدة اليد اليمنى.

مثال\(\PageIndex{3}\): Angular Momentum of a Robot Arm

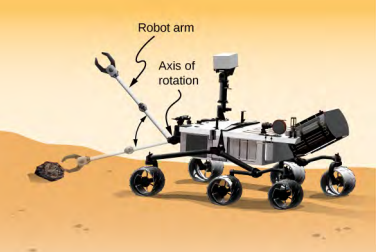
يبلغ طول ذراع الروبوت الموجود على مركبة المريخ مثل Curiosity الموضح في الشكل\(\PageIndex{5}\) 1.0 متر ويحتوي على ملقط في الطرف الحر لالتقاط الصخور. تبلغ كتلة الذراع 2.0 كجم وكتلة الملقط 1.0 كجم (الشكل\(\PageIndex{5}\)). يتحرك ذراع الروبوت والملقط من السكون إلى\(\omega\) = 0.1\(\pi\) راد/ثانية في 0.1 ثانية، ويدور لأسفل ويلتقط صخرة المريخ التي كتلتها 1.5 كجم. محور الدوران هو النقطة التي يتصل فيها ذراع الروبوت بالمركبة.

1. ما مقدار الزخم الزاوي لذراع الروبوت في حد ذاته حول محور الدوران بعد 0.1 ثانية عندما يتوقف الذراع عن التسارع؟
2. ما مقدار الزخم الزاوي لذراع الروبوت عندما تكون صخرة المريخ في ملقطها وتدور لأعلى؟
3. عندما لا تحتوي الذراع على صخرة في الملقط، ما عزم الدوران حول النقطة التي يتصل فيها الذراع بالمركبة الجوالة عندما تتسارع من السكون إلى سرعتها الزاوية النهائية؟

الشكل\(\PageIndex{5}\): ذراع روبوت على مركبة روفر المريخ يتأرجح لأسفل ويلتقط صخرة المريخ. (الائتمان: تعديل العمل من قبل ناسا/JPL-Caltech)

إستراتيجية

نستخدم المعادلة\ ref {11.9} للعثور على الزخم الزاوي في التكوينات المختلفة. عندما يدور الذراع لأسفل، تعطي القاعدة اليمنى متجه الزخم الزاوي الموجه خارج الصفحة، والذي سنسميه اتجاه z الموجب. عندما يدور الذراع لأعلى، تعطي القاعدة اليمنى اتجاه متجه الزخم الزاوي في الصفحة أو في اتجاه z السالب. لحظة القصور الذاتي هي مجموع اللحظات الفردية من القصور الذاتي. يمكن تقريب الذراع بقضيب صلب، ويمكن تقريب الملقط وصخور المريخ ككتل نقطية تقع على مسافة 1 متر من الأصل. بالنسبة للجزء (ج)، نستخدم قانون نيوتن الثاني للحركة للدوران لإيجاد عزم الدوران على ذراع الروبوت.

الحل

1. نكتب اللحظات الفردية من القصور الذاتي، لدينا

• ذراع الروبوت:\[I_{R} = \frac{1}{3} m_{R} r^{2} = \frac{1}{3} (2.00\; kg)(1.00\; m)^{2} = \frac{2}{3}\; kg\; \cdotp m^{2} \ldotp\]
• ملقط:\[I_{F} = m_{F} r^{2} = (1.0\; kg)(1.0\; m)^{2} = 1.0\; kg\; \cdotp m^{2} \ldotp\]
• صخرة المريخ:\[I_{MR} = m_{MR} r^{2} = (1.5\; kg)(1.0\; m)^{2} = 1.5\; kg\; \cdotp m^{2} \ldotp\]

لذلك، بدون صخرة المريخ، تكون اللحظة الإجمالية للقصور الذاتي هي

\[I_{Total} = I_{R} + I_{F} = 1.67\; kg\; \cdotp m^{2}\]

وحجم الزخم الزاوي هو

\[L = I \omega = (1.67\; kg\; \cdotp m^{2})(0.1 \pi\; rad/s) = 0.17 \pi\; kg\; \cdotp m^{2}/s \ldotp\]

يتم توجيه متجه الزخم الزاوي خارج الصفحة في\(\hat{k}\) الاتجاه لأن ذراع الروبوت يدور عكس اتجاه عقارب الساعة.

2. يجب علينا تضمين صخرة المريخ في حساب لحظة القصور الذاتي، لذلك لدينا\[I_{Total} = I_{R} + I_{F} + I_{MR} = 3.17\; kg\; \cdotp m^{2}\]\[L = I \omega = (3.17\; kg\; \cdotp m^{2})(0.1 \pi\; rad/s) = 0.32 \pi\; kg\; \cdotp m^{2}/s \ldotp\] والآن يتم توجيه متجه الزخم الزاوي إلى الصفحة في\(− \hat{k}\) الاتجاه، من خلال القاعدة اليمنى، حيث أن ذراع الروبوت يدور الآن في اتجاه عقارب الساعة.
3. نجد عزم الدوران عندما لا يحتوي الذراع على الصخرة عن طريق أخذ مشتق الزخم الزاوي باستخدام المعادلة\ ref {11.8}\(\frac{d \vec{L}}{dt} = \sum \vec{\tau}\). ولكن بما أن L = I\(\omega\)، ومع إدراك أن اتجاه الزخم الزاوي ومتجهات عزم الدوران يقع على طول محور الدوران، يمكننا قمع رمز\[\frac{dL}{dt} = \frac{d (I \omega)}{dt} = I \frac{d \omega}{dt} = I \alpha = \sum \tau,\] المتجه وإيجاد قانون نيوتن الثاني للدوران. نظرًا لأنه\(\alpha = \frac{0.1 \pi\; rad/s}{0.1\; s} = \pi\; rad/s^{2}\) يمكننا حساب عزم الدوران الصافي:\[\sum \tau = I \alpha = (1.67\; kg\; \cdotp m^{2})(\pi\; rad/s^{2}) = 1.67 \pi\; N\; \cdotp m \ldotp\]

الأهمية

الزخم الزاوي في (أ) أقل من (ب) بسبب حقيقة أن لحظة القصور الذاتي في (ب) أكبر من (أ)، في حين أن السرعة الزاوية هي نفسها.

التمارين الرياضية\(\PageIndex{3}\)

ما مقدار الحركة الزاوي الأكبر: كرة صلبة كتلتها م تدور بتردد زاوي ثابت\(\omega_{0}\) حول المحور z، أم أسطوانة صلبة لها نفس الكتلة ومعدل دوران حول المحور z؟

محاكاة

قم بزيارة المحاكاة التفاعلية للزخم الزاوي بجامعة كولورادو لمعرفة المزيد عن الزخم الزاوي.