11.2: رولينغ موشن
- Page ID
- 199878
- وصف فيزياء الحركة الدورانية دون الانزلاق
- اشرح كيف ترتبط المتغيرات الخطية بالمتغيرات الزاوية لحالة الحركة الدورانية دون الانزلاق
- ابحث عن التسارع الخطي والزاوي في الحركة الدورانية مع الانزلاق وبدونه
- احسب قوة الاحتكاك الثابتة المرتبطة بحركة التدحرج دون الانزلاق
- استخدم الحفاظ على الطاقة لتحليل الحركة المتدحرجة
الحركة الدورانية هي تلك التركيبة الشائعة من الحركة الدورانية والانتقالية التي نراها في كل مكان وكل يوم. فكر في المواقف المختلفة للعجلات التي تتحرك على سيارة على طول طريق سريع، أو عجلات على متن طائرة تهبط على مدرج، أو عجلات على مستكشف آلي على كوكب آخر. يعد فهم القوى وعزم الدوران المشاركة في الحركة الدورانية عاملاً حاسمًا في العديد من أنواع المواقف المختلفة.
لتحليل حركة التدحرج في هذا الفصل، راجع الشكل 10.5.4 في دوران المحور الثابت للعثور على لحظات القصور الذاتي لبعض الأجسام الهندسية الشائعة. قد تجدها مفيدة أيضًا في العمليات الحسابية الأخرى التي تتضمن الدوران.
حركة متدحرجة بدون انزلاق
لاحظ الناس حركة التدحرج دون الانزلاق منذ اختراع العجلة. على سبيل المثال، يمكننا أن ننظر إلى تفاعل إطارات السيارة وسطح الطريق. إذا قام السائق بالضغط على دواسة الوقود على الأرض، بحيث تدور الإطارات دون أن تتحرك السيارة للأمام، فيجب أن يكون هناك احتكاك حركي بين العجلات وسطح الطريق. إذا قام السائق بالضغط على دواسة الوقود ببطء، مما يتسبب في تحرك السيارة للأمام، فإن الإطارات تتدحرج دون انزلاق. من المدهش لمعظم الناس أن الجزء السفلي من العجلة في حالة راحة فيما يتعلق بالأرض، مما يشير إلى ضرورة وجود احتكاك ثابت بين الإطارات وسطح الطريق. في الشكل\(\PageIndex{1}\)، تتحرك الدراجة مع بقاء الراكب في وضع مستقيم. تتلامس الإطارات مع سطح الطريق، وعلى الرغم من أنها تدور، فإن قيعان الإطارات تتشوه قليلاً، ولا تنزلق، وهي في حالة راحة فيما يتعلق بسطح الطريق لفترة زمنية قابلة للقياس. يجب أن يكون هناك احتكاك ثابت بين الإطار وسطح الطريق حتى يكون الأمر كذلك.
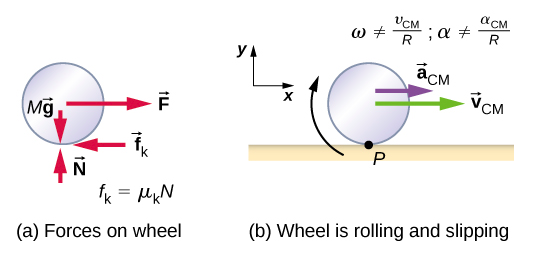
لتحليل التدحرج دون الانزلاق، نقوم أولاً باستخلاص المتغيرات الخطية للسرعة وتسارع مركز كتلة العجلة من حيث المتغيرات الزاوية التي تصف حركة العجلة. يظهر الموقف في الشكل\(\PageIndex{2}\).
من الشكل\(\PageIndex{2}\) (أ)، نرى متجهات القوة المشاركة في منع العجلة من الانزلاق. في (ب)، تكون النقطة P التي تلامس السطح في حالة سكون بالنسبة للسطح. بالنسبة إلى مركز الكتلة، فإن النقطة P لها السرعة −R\(\omega \hat{i}\)، حيث R هي نصف قطر العجلة\(\omega\) وهي السرعة الزاوية للعجلة حول محورها. نظرًا لأن العجلة تدور، فإن سرعة P فيما يتعلق بالسطح هي سرعتها فيما يتعلق بمركز الكتلة بالإضافة إلى سرعة مركز الكتلة فيما يتعلق بالسطح:
\[\vec{v}_{P} = -R \omega \hat{i} + v_{CM} \hat{i} \ldotp\]
نظرًا لأن سرعة P بالنسبة للسطح هي صفر، v P = 0، فهذا يعني أن
\[v_{CM} = R \omega \ldotp \label{11.1}\]
وبالتالي، فإن سرعة مركز كتلة العجلة هي نصف قطرها مضروبًا في السرعة الزاوية حول محورها. نعرض تطابق المتغير الخطي على الجانب الأيسر من المعادلة مع المتغير الزاوي على الجانب الأيمن من المعادلة. يتم ذلك أدناه للتسارع الخطي.
إذا فرقنا المعادلة\ ref {11.1} على الجانب الأيسر من المعادلة، نحصل على تعبير عن التسارع الخطي لمركز الكتلة. على الجانب الأيمن من المعادلة، R هو ثابت ومنذ ذلك الحين\(\alpha = \frac{d \omega}{dt}\)، لدينا
\[a_{CM} = R \alpha \ldotp \label{11.2}\]
علاوة على ذلك، يمكننا إيجاد المسافة التي تقطعها العجلة من حيث المتغيرات الزاوية بالرجوع إلى الشكل\(\PageIndex{3}\). عندما تتحرك العجلة من النقطة A إلى النقطة B، يتم رسم خرائط سطحها الخارجي على الأرض من خلال المسافة المقطوعة بالضبط، وهي d CM.
نرى من الشكل\(\PageIndex{3}\) أن طول السطح الخارجي الذي يرسم على الأرض هو طول القوس R\(\theta\). نحصل على معادلة المسافتين
\[d_{CM} = R \theta \ldotp \label{11.3}\]
تتدحرج أسطوانة صلبة على مستوى مائل دون الانزلاق، بدءًا من السكون. كتلته m ونصف قطره r. (أ) ما عجلته؟ (ب) ما هي الحالة التي يجب أن\(\mu_{S}\) يفي بها معامل الاحتكاك الساكن حتى لا تنزلق الأسطوانة؟
إستراتيجية
ارسم رسمًا تخطيطيًا ومخططًا للجسم الحر، واختر نظام الإحداثيات. نضع x في الاتجاه لأسفل المستوى و y لأعلى عموديًا على المستوى. حدد القوى المشاركة. هذه هي القوة العادية وقوة الجاذبية والقوة الناتجة عن الاحتكاك. اكتب قوانين نيوتن في الاتجاهين x و y، وقانون نيوتن للدوران، ثم حل التسارع والقوة الناتجة عن الاحتكاك.
الحل
- يظهر مخطط الجسم الحر والرسم التخطيطي في الشكل\(\PageIndex{4}\)، بما في ذلك القوة العادية ومكونات الوزن وقوة الاحتكاك الإستاتيكية. بالكاد يوجد احتكاك كافٍ للحفاظ على دوران الأسطوانة دون الانزلاق. نظرًا لعدم وجود انزلاق، فإن حجم قوة الاحتكاك أقل من أو يساوي\(\mu_{S}\) N. كتابة قوانين نيوتن في الاتجاهين x و y، لدينا
\[\sum F_{x} = ma_{x};\; \sum F_{y} = ma_{y} \ldotp\]
الاستبدال من مخطط الجسم الحر
\[\begin{split} mg \sin \theta - f_{s} & = m(a_{CM}) x, \\ N - mg \cos \theta & = 0 \end{split}\]
يمكننا بعد ذلك حل التسارع الخطي لمركز الكتلة من هذه المعادلات:
\[a_{CM} = g\sin \theta - \frac{f_s}{m} \ldotp\]
ومع ذلك، من المفيد التعبير عن التسارع الخطي من حيث لحظة القصور الذاتي. لهذا، نكتب قانون نيوتن الثاني للدوران،
\[\sum \tau_{CM} = I_{CM} \alpha \ldotp\]
يتم حساب عزم الدوران حول المحور من خلال مركز كتلة الأسطوانة. يتم توفير عزم الدوران الوحيد غير الصفري من خلال قوة الاحتكاك. لدينا
\[f_{s} r = I_{CM} \alpha \ldotp\]
أخيرًا، يرتبط التسارع الخطي بالتسارع الزاوي بواسطة
\[(a_{CM})_{x} = r \alpha \ldotp\]
يمكن استخدام هذه المعادلات لحل CM و f S من حيث لحظة القصور الذاتي، حيث قمنا بإسقاط x-subcept.\(\alpha\) نكتب CM بدلالة المكون الرأسي للجاذبية وقوة الاحتكاك، ونجري البدائل التالية.
\[f_{S} = \frac{I_{CM} \alpha}{r} = \frac{I_{CM} a_{CM}}{r^{2}}\]
من هذا نحصل عليه
\[\begin{split} a_{CM} & = g \sin \theta - \frac{I_{CM} a_{CM}}{mr^{2}}, \\ & = \frac{mg \sin \theta}{m + \left(\dfrac{I_{CM}}{r^{2}}\right)} \ldotp \end{split}\]
لاحظ أن هذه النتيجة مستقلة عن معامل الاحتكاك الساكن،\(\mu_{s}\).
نظرًا لأن لدينا أسطوانة صلبة، من الشكل 10.5.4، لدينا I CM =\(\frac{mr^{2}}{2}\) و
\[a_{CM} = \frac{mg \sin \theta}{m + \left(\dfrac{mr^{2}}{2r^{2}}\right)} = \frac{2}{3} g \sin \theta \ldotp\]
لذلك، لدينا
\[\alpha = \frac{a_{CM}}{r} = \frac{2}{3r} g \sin \theta \ldotp\]
- بسبب عدم حدوث الانزلاق، f S ≤\(\mu_{s}\) N. حل قوة الاحتكاك، $f_ {s} = I_ {CM}\ frac {\ alpha} {r} = I_ {CM}\ frac {(a_ {CM})} {r^ {2}} = =\ يسار (\ dfrac {I_ {CM} {r} {2}}\ يمين)\ يسار (\ dfrac {I_ {CM} {r} {2}} {mg\ sin\ theta} {م +\ يسار (\ dfrac {I_ {CM}} {r^ {2}}\ يمين)}\ يمين) =\ frac {mg I_ {CM}\ سين\ ثيتا} {mr ^ {2} + I_ {CM}\ lDotP$استبدال هذا التعبير بشرط عدم الانزلاق، مع ملاحظة أن N = mg cos\(\theta\)، لدينا $\ frac {mg I_ {CM}\ sin\ theta} {mr ^ {2} + I_ {CM}}\ leq\ mu_ {s} mg\ cos\ theta$أو $$\ mu_ {s}\ geq\ frac {\ تان\ ثيتا} {1 +\ يسار (\ dfrac {mr^ {2}} {I_ {CM}}\ يمين)}\ lDotP$$للمادة الصلبة الأسطوانة، تصبح هذه $$\ mu_ {s}\ geq\ frac {\ tan\ theta} {1 +\ يسار (\ dfrac {2}} {mr ^ {2}}\ يمين)} =\ فراك {1} {3}\ تان\ ثيتا\ ldotp $$
الدلالة
- التسارع الخطي يتناسب خطيًا مع الخطيئة\(\theta\). وبالتالي، كلما زادت زاوية المنحدر، زاد التسارع الخطي، كما هو متوقع. ومع ذلك، فإن التسارع الزاوي يتناسب خطيًا مع الخطيئة\(\theta\) ويتناسب عكسيًا مع نصف قطر الأسطوانة. وبالتالي، كلما زاد نصف القطر، قل التسارع الزاوي.
- حتى لا يحدث أي انزلاق، يجب أن يكون معامل الاحتكاك الإستاتيكي أكبر من أو يساوي\(\frac{1}{3}\) تان\(\theta\). وبالتالي، كلما زادت زاوية المنحدر، يجب أن يكون معامل الاحتكاك الساكن أكبر لمنع الأسطوانة من الانزلاق.
توجد أسطوانة مجوفة على منحدر بزاوية 60 درجة. معامل الاحتكاك الساكن على السطح هو\(\mu_{s}\) = 0.6. (أ) هل تتدحرج الأسطوانة دون انزلاق؟ (ب) هل ستتدحرج الأسطوانة الصلبة دون انزلاق؟
من المفيد تكرار المعادلة المشتقة في هذا المثال لتسريع جسم يتدحرج دون انزلاق:
\[a_{CM} = \frac{mg \sin \theta}{m + \left(\dfrac{I_{CM}}{r^{2}}\right)} \ldotp \label{11.4}\]
هذه معادلة مفيدة جدًا لحل المشكلات التي تتضمن التدحرج دون الانزلاق. لاحظ أن التسارع أقل من ذلك الخاص بجسم ينزلق إلى أسفل مستوى خالٍ من الاحتكاك بدون دوران. سيكون التسارع مختلفًا أيضًا بالنسبة لأسطوانتين دوارتين بقصور ذاتية دورانية مختلفة.
حركة التدحرج مع الانزلاق
في حالة حركة التدحرج مع الانزلاق، يجب أن نستخدم معامل الاحتكاك الحركي، الذي يؤدي إلى ظهور قوة الاحتكاك الحركي لأن الاحتكاك الساكن غير موجود. يظهر الموقف في الشكل\(\PageIndex{5}\). في حالة الانزلاق، v CM − R\(\omega\) 0، لأن النقطة P على العجلة ليست في وضع السكون على السطح، و v P 0. وهكذا\(\omega\)،\(\frac{v_{CM}}{R}\)،\(\alpha \neq \frac{a_{CM}}{R}\).
تتدحرج أسطوانة صلبة على مستوى مائل من السكون وتتعرض للانزلاق (الشكل\(\PageIndex{6}\)). كتلته m ونصف قطره r. (أ) ما عجلته الخطية؟ (ب) ما التسارع الزاوي حول محور يمر بمركز الكتلة؟
إستراتيجية
ارسم رسمًا تخطيطيًا ومخططًا للجسم الحر يوضح القوى المعنية. يشبه مخطط الجسم الحر حالة عدم الانزلاق باستثناء قوة الاحتكاك، التي تكون حركية وليست ثابتة. استخدم قانون نيوتن الثاني لحل التسارع في الاتجاه x. استخدم قانون نيوتن الثاني للدوران لحل التسارع الزاوي.
الحل
مجموع القوى في الاتجاه y هو صفر، وبالتالي فإن قوة الاحتكاك هي الآن f k =\(\mu_{k}\) N =\(\mu_{k}\) mg cos\(\theta\). يصبح قانون نيوتن الثاني في الاتجاه x
\[\sum F_{x} = ma_{x}, \nonumber\]
\[mg \sin \theta - \mu_{k} mg \cos \theta = m(a_{CM})_{x}, \nonumber\]
أو
\[(a_{CM})_{x} = g(\sin \theta - \mu_{k} \cos \theta) \ldotp \nonumber\]
توفر قوة الاحتكاك عزم الدوران الوحيد حول المحور من خلال مركز الكتلة، لذلك يصبح قانون نيوتن الثاني للدوران
\[\sum \tau_{CM} = I_{CM} \alpha, \nonumber\]
\[f_{k} r = I_{CM} \alpha = \frac{1}{2} mr^{2} \alpha \ldotp \nonumber\]
حل المشكلة\(\alpha\)، لدينا
\[\alpha = \frac{2f_{k}}{mr} = \frac{2 \mu_{k} g \cos \theta}{r} \ldotp \nonumber\]
الدلالة
نكتب التسارع الخطي والزاوي من حيث معامل الاحتكاك الحركي. التسارع الخطي هو نفسه الذي يوجد لجسم ينزلق إلى أسفل مستوى مائل مع احتكاك حركي. يتناسب التسارع الزاوي حول محور الدوران خطيًا مع القوة العادية، والتي تعتمد على جيب التمام لزاوية الميل. مثل\(\theta\) → 90 درجة، تذهب هذه القوة إلى الصفر، وبالتالي، يذهب التسارع الزاوي إلى الصفر.
الحفاظ على الطاقة الميكانيكية في الحركة الدورانية
في الفصل السابق، قدمنا طاقة الحركة الدورانية. يحمل أي جسم متداول طاقة حركية دورانية، بالإضافة إلى طاقة حركية انتقالية وطاقة كامنة إذا تطلب النظام ذلك. بما في ذلك الطاقة الكامنة للجاذبية، فإن إجمالي الطاقة الميكانيكية لجسم يتدحرج هو
\[E_{T} = \frac{1}{2} mv^{2}_{CM} + \frac{1}{2} I_{CM} \omega^{2} + mgh \ldotp\]
في حالة عدم وجود أي قوى غير محافظة من شأنها إخراج الطاقة من النظام في شكل حرارة، يتم الحفاظ على الطاقة الكلية للجسم المتداول دون الانزلاق وتكون ثابتة طوال الحركة. ومن الأمثلة على الحالات التي لا يتم فيها حفظ الطاقة الجسم المتداول الذي ينزلق، وإنتاج الحرارة نتيجة الاحتكاك الحركي، والجسم المتداول الذي يواجه مقاومة الهواء.
قد تسأل لماذا يحافظ الجسم المتداول الذي لا ينزلق على الطاقة، لأن قوة الاحتكاك الساكنة غير محافظة. يمكن العثور على الإجابة بالرجوع إلى الشكل\(\PageIndex{2}\). تكون النقطة P الملامسة للسطح في حالة سكون فيما يتعلق بالسطح. لذلك، فإن إزاحته متناهية الصغر d\(\vec{r}\) فيما يتعلق بالسطح هي صفر، والعمل الإضافي الذي تقوم به قوة الاحتكاك الثابتة هو صفر. يمكننا تطبيق الحفاظ على الطاقة في دراستنا للحركة المتدحرجة لإخراج بعض النتائج المثيرة للاهتمام.
تم نشر مركبة كيوريوسيتي الجوالة\(\PageIndex{7}\)، الموضحة في الشكل، على المريخ في 6 أغسطس 2012. يبلغ نصف قطر عجلات الروفر 25 سم. لنفترض أن رواد الفضاء وصلوا إلى المريخ في عام 2050 ووجدوا Curiosity المعطل الآن على جانب الحوض. أثناء تفكيك المركبة الجوالة، يفقد رائد الفضاء بطريق الخطأ قبضته على إحدى العجلات، التي تتدحرج دون الانزلاق إلى قاع الحوض على عمق 25 مترًا. إذا كانت كتلة العجلة ٥ كجم، فما سرعتها في قاع الحوض؟
إستراتيجية
نحن نستخدم الحفاظ على الطاقة الميكانيكية لتحليل المشكلة. في الجزء العلوي من التل، تكون العجلة في حالة راحة ولديها طاقة كامنة فقط. في الجزء السفلي من الحوض، تحتوي العجلة على طاقة حركية دورانية وانتقالية، والتي يجب أن تكون مساوية للطاقة الكامنة الأولية من خلال الحفاظ على الطاقة. نظرًا لأن العجلة تدور دون انزلاق، فإننا نستخدم العلاقة v CM = r\(\omega\) لربط المتغيرات الانتقالية بالمتغيرات الدورانية في معادلة الحفاظ على الطاقة. ثم نقوم بحل السرعة. من الشكل\(\PageIndex{7}\)، نرى أن الأسطوانة المجوفة تمثل تقديرًا تقريبيًا جيدًا للعجلة، لذلك يمكننا استخدام لحظة القصور الذاتي هذه لتبسيط الحساب.
الحل
الطاقة في الجزء العلوي من الحوض تساوي الطاقة في الأسفل:
\[mgh = \frac{1}{2} mv_{CM}^{2} + \frac{1}{2} I_{CM} \omega^{2} \ldotp \nonumber\]
الكميات المعروفة هي I CM = mr 2، r = 0.25 م، و h = 25.0 م.
نعيد كتابة معادلة الحفاظ على الطاقة\(\omega\) بالحذف باستخدام\(\omega\) = v CM r. لدينا
\[mgh = \frac{1}{2} mv_{CM}^{2} + \frac{1}{2} mr^{2} \frac{v_{CM}^{2}}{r^{2}} \nonumber\]
أو
\[gh = \frac{1}{2} v_{CM}^{2} + \frac{1}{2} v_{CM}^{2} \Rightarrow v_{CM} = \sqrt{gh} \ldotp \nonumber\]
تبلغ سرعة الجاذبية في المريخ 3.71 متر/ثانية 2، مما يعطي مقدار السرعة في الجزء السفلي من الحوض كما يلي:
\[v_{CM} = \sqrt{(3.71\; m/s^{2})(25.0\; m)} = 9.63\; m/s \ldotp \nonumber\]
الدلالة
هذه نتيجة دقيقة إلى حد ما بالنظر إلى أن الغلاف الجوي للمريخ قليل جدًا، وأن فقدان الطاقة بسبب مقاومة الهواء سيكون ضئيلًا. تفترض النتيجة أيضًا أن التضاريس سلسة، بحيث لا تواجه العجلة الصخور والصدمات على طول الطريق.
أيضًا، في هذا المثال، يتم تقاسم الطاقة الحركية، أو طاقة الحركة، بالتساوي بين الحركة الخطية والحركة الدورانية. إذا نظرنا إلى لحظات القصور الذاتي في الشكل 10.5.4، نرى أن الأسطوانة المجوفة تحتوي على أكبر لحظة من القصور الذاتي لنصف قطر وكتلة معينين. إذا كانت عجلات المسبار صلبة ومقربة بأسطوانات صلبة، على سبيل المثال، فستكون هناك طاقة حركية في الحركة الخطية أكثر من الحركة الدورانية. وهذا من شأنه أن يعطي العجلة سرعة خطية أكبر من تقريب الأسطوانة المجوفة. وبالتالي، ستصل الأسطوانة الصلبة إلى قاع الحوض بشكل أسرع من الأسطوانة المجوفة.


