7.4: نظرية الشغل والطاقة
- Page ID
- 200024
- طبّق نظرية الشغل والطاقة لإيجاد معلومات عن حركة الجسم، بمعلومية القوى المؤثِّرة عليه
- استخدم نظرية الشغل والطاقة لإيجاد معلومات عن القوى المؤثِّرة على الجسم، بمعلومية معلومات عن حركته
لقد ناقشنا كيفية إيجاد العمل المنجز على الجسيم بواسطة القوى التي تعمل عليه، ولكن كيف يتجلى هذا العمل في حركة الجسيم؟ وفقًا لقانون نيوتن الثاني للحركة، فإن مجموع كل القوى المؤثرة على الجسم، أو القوة الكلية، يحدد معدل التغير في كمية حركة الجسيم، أو حركته. لذلك، يجب أن نأخذ في الاعتبار العمل الذي تقوم به جميع القوى المؤثرة على الجسيم، أو الشغل الكلي، لنرى مدى تأثيره على حركة الجسيم.
لنبدأ بالنظر إلى العمل الصافي المنجز على الجسيم أثناء تحركه فوق الإزاحة متناهية الصغر، وهي المنتج النقطي للقوة الصافية والإزاحة:
\[dW_{net} = \vec{F}_{net} \cdotp d \vec{r}. \nonumber\]
يخبرنا قانون نيوتن الثاني بذلك
\[\vec{F}_{net} = m \left(\dfrac{d \vec{v}}{dt}\right) \nonumber\]
وبالتالي
\[dW_{net} = m \left(\dfrac{d \vec{v}}{dt}\right) \cdotp d \vec{r}. \nonumber\]
بالنسبة للوظائف الرياضية التي تصف حركة جسيم فيزيائي، يمكننا إعادة ترتيب الفوارق dt، وما إلى ذلك، ككميات جبرية في هذا التعبير، أي
\[\begin{align*} dW_{net} &= m \left(\dfrac{d \vec{v}}{dt}\right) \cdotp d \vec{r} \\[4pt] &= m\, d \vec{v}\; \cdotp \left(\dfrac{d \vec{r}}{dt}\right) \\[4pt] &= m \vec{v}\; \cdotp d \vec{v}, \end{align*}\]
حيث قمنا باستبدال السرعة بالمشتق الزمني للإزاحة واستخدمنا خاصية الإبدال للمنتج النقطي. نظرًا لأن مشتقات وتكاملات الأرقام القياسية ربما تكون أكثر شيوعًا بالنسبة لك في هذه المرحلة، فإننا نعبر عن منتج النقاط من حيث الإحداثيات الديكارتية قبل أن ندمج بين أي نقطتين A و B على مسار الجسيم. هذا يعطينا العمل الصافي المنجز على الجسيم:
\[\begin{align} W_{net,\; AB} & = \int_{A}^{B} (mv_{x} dv_{x} + mv_{y}dv_{y} + mv_{z}dv_{z} \\[4pt] & = \frac{1}{2} m \left| v_{x}^{2} + v_{y}^{2} + v_{z}^{2} \right|_{A}^{B} = \left|\frac{1}{2} mv^{2} \right|_{A}^{B} = K_{B} - K_{A} \ldotp \end{align} \label{7.8}\]
في الخطوة الوسطى، استخدمنا حقيقة أن مربع السرعة هو مجموع مربعات مكوناته الكارتيزية، وفي الخطوة الأخيرة، استخدمنا تعريف الطاقة الحركية للجسيم. هذه النتيجة المهمة تسمى نظرية الشغل والطاقة.
العمل الكلي الذي تم على جسيم يساوي التغيير في الطاقة الحركية للجسيم:
\[W_{net} = K_{B} - K_{A} \ldotp \label{7.9}\]

وفقًا لهذه النظرية، عندما يتباطأ جسم ما، تكون طاقة حركته النهائية أقل من طاقته الحركية الأولية، ويكون التغير في طاقة حركته سالبًا، وكذلك يكون إجمالي العمل المنجز عليه. إذا زادت سرعة الكائن، فإن العمل الصافي المنجز عليه يكون موجبًا. عند حساب العمل الصافي، يجب تضمين جميع القوى التي تعمل على كائن. إذا تركت أي قوى تؤثر على كائن ما، أو إذا قمت بتضمين أي قوى لا تعمل عليه، فستحصل على نتيجة خاطئة.
تكمن أهمية نظرية الشغل والطاقة، والتعميمات الإضافية التي تؤدي إليها، في أنها تجعل بعض أنواع الحسابات أسهل بكثير في الإنجاز مقارنة بمحاولة حل قانون نيوتن الثاني. على سبيل المثال، في القسم الخاص بقوانين نيوتن للحركة، وجدنا سرعة جسم ينزلق إلى أسفل مستوى خالٍ من الاحتكاك عن طريق حل قانون نيوتن الثاني للعجلة واستخدام المعادلات الحركية للعجلة الثابتة، والحصول على
\[v_{f}^{2} = v_{i}^{2} + 2g(s_{f} - s_{i}) \sin \theta,\]
\(s\)أين الإزاحة أسفل الطائرة.
يمكننا أيضًا الحصول على هذه النتيجة من نظرية الشغل والطاقة (المعادلة\ ref {7.9}). نظرًا لأن قوتين فقط تعملان على الجسم - الجاذبية والقوة العادية - والقوة العادية لا تقوم بأي عمل، فإن العمل الصافي هو مجرد العمل الذي تقوم به الجاذبية. هذا يعتمد فقط على وزن الكائن والفرق في الارتفاع، لذلك
\[W_{net} = W_{grav} = -mg (y_{f} - y_{i}),\]
أين\(y\) هو الإيجابي. تقول نظرية الشغل والطاقة أن هذا يساوي التغيير في الطاقة الحركية:
\[-mg (y_{f} - y_{i}) = \frac{1}{2} (v_{f}^{2} - v_{i}^{2}) \ldotp\]
باستخدام المثلث الأيمن، يمكننا أن نرى ذلك
\[(y_f − y_i) = (s_f − s-i)\sin \theta, \nonumber\]
وبالتالي فإن نتيجة السرعة النهائية هي نفسها.
ما الذي يُكتسب باستخدام نظرية الشغل والطاقة؟ الجواب هو أنه بالنسبة لسطح مستوٍ خالٍ من الاحتكاك، ليس كثيرًا. ومع ذلك، من السهل حل قانون نيوتن الثاني لهذه الحالة بالذات فقط، في حين أن نظرية الشغل والطاقة تعطي السرعة النهائية لأي سطح غير احتكاكي. بالنسبة للسطح المنحني العشوائي، فإن القوة العادية ليست ثابتة، وقد يكون من الصعب أو المستحيل حل قانون نيوتن الثاني تحليليًا. سواء كانت ثابتة أم لا، بالنسبة للحركة على سطح ما، فإن القوة العادية لا تقوم أبدًا بأي عمل، لأنها متعامدة مع الإزاحة. يتجنب الحساب باستخدام نظرية العمل والطاقة هذه الصعوبة وينطبق على المواقف الأكثر عمومية.
- ارسم مخططًا للجسم الحر لكل قوة على الكائن.
- حدد ما إذا كانت كل قوة تعمل على الإزاحة في الشكل أم لا. تأكد من الاحتفاظ بأي علامات إيجابية أو سلبية في العمل المنجز.
- اجمع إجمالي مقدار العمل الذي أنجزته كل قوة.
- قم بتعيين هذا العمل الإجمالي مساويًا للتغير في الطاقة الحركية وحل أي معامل غير معروف.
- تحقق من إجاباتك. إذا كان الجسم يتحرك بسرعة ثابتة أو تسارع صفري، يجب أن يكون إجمالي العمل المنجز صفرًا ومطابقًا للتغير في الطاقة الحركية. إذا كان إجمالي العمل موجبًا، يجب أن يكون الكائن قد زاد من سرعة الطاقة الحركية أو زيادتها. إذا كان إجمالي العمل سالبًا، يجب أن يكون الكائن قد تباطأ أو انخفض طاقة الحركة
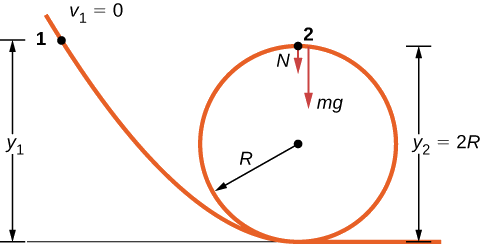
يشتمل المسار الخالي من الاحتكاك لسيارة لعبة على دائرة نصف قطرها حلقة\(R\). ما هو الارتفاع الذي يجب أن تضعه السيارة عند قياسها من أسفل الحلقة بحيث تبدأ من وضع السكون على الجزء المقترب من المسار وتنطلق في جميع أنحاء الحلقة؟
إستراتيجية
تم رسم مخطط الجسم الحر في الموضع النهائي للكائن في الشكل\(\PageIndex{2}\). عمل الجاذبية هو العمل الوحيد الذي يتم إجراؤه خلال الإزاحة والذي ليس صفرًا. نظرًا لأن الوزن يشير في نفس اتجاه الإزاحة الرأسية الصافية، فإن إجمالي العمل الذي تقوم به قوة الجاذبية يكون موجبًا. من نظرية الشغل والطاقة، يحدد ارتفاع البداية سرعة السيارة في الجزء العلوي من الحلقة،
\[mg(y_{2} - y_{1}) = \dfrac{1}{2} mv_{2}^{2}, \nonumber\]
حيث يظهر الترميز في الشكل المصاحب. في الجزء العلوي من الحلقة، تنخفض القوة الطبيعية والجاذبية معًا ويكون التسارع جاذبًا، لذلك
\[a_{top} = \dfrac{F}{m} = \dfrac{N + mg}{m} = \frac{v_{2}^{2}}{R} \ldotp \nonumber\]
شرط الحفاظ على الاتصال بالمسار هو أنه يجب أن تكون هناك بعض القوة العادية، مهما كانت طفيفة؛ أي\(N > 0\). كبديل عن\(v_{2}^{2}\) و\(N\)، يمكننا العثور على الشرط لـ\(y_1\).
الحل
قم بتنفيذ الخطوات في الاستراتيجية للوصول إلى النتيجة المرجوة:
\[N = -mg + \frac{mv_{2}^{2}}{R} = \frac{-mgR + 2mg(y_{1} - 2R)}{R} > 0\; or\; y_{1} > \frac{5R}{2} \ldotp \nonumber\]
الدلالة
على سطح الحلقة، يجب أن يوفر المكون الطبيعي للجاذبية وقوة الاتصال العادية التسارع المركزي للسيارة التي تدور حول الحلقة. يؤدي المكون العرضي للجاذبية إلى إبطاء السيارة أو تسريعها. سيكتشف الطفل مدى ارتفاع تشغيل السيارة عن طريق التجربة والخطأ، ولكن الآن بعد أن عرفت نظرية العمل والطاقة، يمكنك التنبؤ بالحد الأدنى للارتفاع (بالإضافة إلى النتائج الأخرى الأكثر فائدة) من المبادئ الفيزيائية. باستخدام نظرية الشغل والطاقة، لم يكن عليك حل معادلة تفاضلية لتحديد الارتفاع.
لنفترض أن نصف قطر حلقة الحلقة في المثال\(\PageIndex{1}\) هو 15 سم وتبدأ سيارة اللعبة من السكون على ارتفاع 45 سم فوق القاع. ما سرعتها في الجزء العلوي من الحلقة؟
في الحالات التي تكون فيها حركة الجسم معروفة، ولكن قيم واحدة أو أكثر من القوى المؤثرة عليه غير معروفة، قد تتمكن من استخدام نظرية الشغل والطاقة للحصول على بعض المعلومات حول القوى. يعتمد العمل على القوة والمسافة التي يعمل بها، لذلك يتم توفير المعلومات عبر منتجهم.
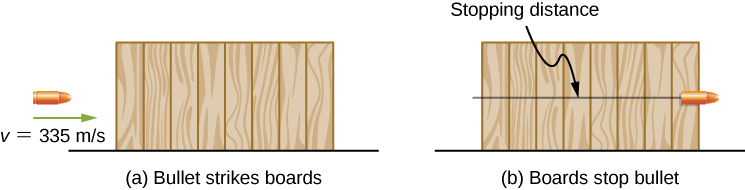
كتلة رصاصة مقدارها ٤٠ حبة (٢٫٦٠ جم) وسرعة كمامة مقدارها ١١٠٠ قدم. /ثانية (335 م/ث). يمكن أن تخترق ثمانية ألواح صنوبر مقاس 1 بوصة، كل منها بسماكة 0.75 بوصة. ما متوسط قوة الإيقاف التي يؤثِّر بها الخشب، كما هو موضَّح في الشكل\(\PageIndex{3}\)؟
إستراتيجية
يمكننا أن نفترض أنه في ظل الظروف العامة المذكورة، تفقد الرصاصة كل طاقتها الحركية التي تخترق الألواح، لذلك تقول نظرية العمل والطاقة أن طاقتها الحركية الأولية تساوي متوسط قوة التوقف مضروبًا في المسافة المخترقة. التغيُّر في طاقة حركة الرصاصة والعمل الكلي المبذول لإيقافها كلاهما سالب، لذلك عندما تكتب نظرية الشغل والطاقة، حيث تساوي الشغل الكلي القوة المتوسطة في مسافة التوقف، فهذا هو ما تحصل عليه. السماكة الإجمالية لثمانية ألواح صنوبر مقاس 1 بوصة تخترقها الرصاصة هي 8 ×\(\frac{3}{4}\) بوصة. = 6 بوصات = 15.2 سم.
الحل
عند تطبيق نظرية الشغل والطاقة، نحصل على
\[W_{net} = - F_{ave} \Delta s_{stop} = - K_{initial} , \nonumber\]
وبالتالي
\[F_{ave} = \frac{\frac{1}{2} mv^{2}}{\Delta s_{stop}} = \frac{\frac{1}{2} (2.66 \times 10^{-3}\; kg)(335\; m/s)^{2}}{0.152\; m} = 960\; N \ldotp \nonumber\]
الدلالة
كان بإمكاننا استخدام قانون نيوتن الثاني وعلم الحركة في هذا المثال، لكن نظرية الشغل والطاقة توفر أيضًا إجابة لحالات أقل بساطة. تمت مناقشة تغلغل الرصاصة، التي أُطلقت عموديًا لأعلى في كتلة من الخشب، في قسم واحد من مقال آصف شاكور الأخير [«لغز فيديو علمي من الرصاص». مدرس الفيزياء (يناير 2015) 53 (1): 15-16]. إذا تم إطلاق الرصاصة في منتصف الكتلة، فإنها تفقد كل طاقتها الحركية وتخترق مسافة أبعد قليلاً مما لو تم إطلاقها خارج المركز. والسبب هو أنه إذا اصطدمت الرصاصة بعيدًا عن المركز، فإنها تحصل على القليل من الطاقة الحركية بعد توقفها عن الاختراق، لأن الكتلة تدور. تشير نظرية الشغل والطاقة إلى أن التغيير الأصغر في الطاقة الحركية ينتج عنه اختراق أصغر. ستفهم المزيد من الفيزياء في هذه المقالة المثيرة للاهتمام بعد الانتهاء من قراءة Angular Momentum.
تعرف على المزيد حول العمل والطاقة في محاكاة PhET هذه (https://phet.colorado.edu/en/simulation/the-ramp) المسماة «المنحدر». حاول تغيير القوة التي تدفع الصندوق وقوة الاحتكاك على طول المنحدر. يمكن فحص مخططات العمل والطاقة لملاحظة إجمالي العمل المنجز والتغيير في الطاقة الحركية للصندوق.


