Skip to main content
Global

5.E: قوانين نيوتن للحركة (تمارين)

  1. Last updated
  2. Save as PDF
  • Page ID
    200104

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أسئلة مفاهيمية

    5.1 القوى

    1. ما الخصائص التي تمتلكها القوى التي تسمح لنا بتصنيفها كمتجهات؟

    5.2 قانون نيوتن الأول

    1. عند أخذ إطار متصل بالأرض بالقصور الذاتي، أي من الكائنات التالية لا يمكن أن تحتوي على إطارات بالقصور الذاتي مرفقة بها، وما هي الإطارات المرجعية بالقصور الذاتي؟
      1. سيارة تتحرك بسرعة ثابتة
      2. سيارة تتسارع
      3. مصعد في السقوط الحر
      4. كبسولة فضائية تدور حول الأرض
      5. مصعد ينزل بشكل موحد
    2. كانت امرأة تنقل صندوقًا مفتوحًا من الكعك إلى حفلة مدرسية. توقفت السيارة التي كانت أمامها فجأة؛ وطبقت الفرامل على الفور. كانت ترتدي حزام الأمان الخاص بها ولم تتعرض لأي أذى جسدي (مجرد قدر كبير من الإحراج)، لكن الكعك طار إلى لوحة القيادة وأصبح «كعكات». اشرح ما حدث.

    5.3 قانون نيوتن الثاني

    1. لماذا يمكننا إهمال قوى مثل تلك التي تجمع الجسد معًا عندما نطبق قانون نيوتن الثاني؟
    2. يتم إلقاء صخرة بشكل مستقيم. في الجزء العلوي من المسار، تكون السرعة صفرًا مؤقتًا. هل يعني هذا أن القوة المؤثرة على الجسم هي صفر؟ اشرح إجابتك.

    5.4 الكتلة والوزن

    1. ما العلاقة بين الوزن والكتلة؟ ما هي الخاصية الجوهرية وغير المتغيرة للجسم؟
    2. كم يبلغ وزن رائد فضاء وزنه 70 كجم في الفضاء، بعيدًا عن أي جسم سماوي؟ ما هي كتلتها في هذا الموقع؟
    3. أي من العبارات التالية دقيقة؟
      1. الكتلة والوزن هما نفس الشيء الذي يتم التعبير عنه بوحدات مختلفة.
      2. إذا لم يكن للجسم وزن، فيجب ألا يكون له كتلة.
      3. إذا كان وزن الجسم مختلفًا، فيجب أن تختلف الكتلة أيضًا.
      4. الكتلة والقصور الذاتي هي مفاهيم مختلفة.
      5. الوزن يتناسب دائمًا مع الكتلة.
    4. عندما تقف على الأرض، تضغط قدميك عليها بقوة تساوي وزنك. لماذا لا تتسارع الأرض بعيدًا عنك؟
    5. كيف يمكنك إعطاء القيمة\(\vec{g}\) في شكل متجه؟

    ٥.٥ قانون نيوتن الثالث

    1. حدد قوى العمل ورد الفعل في الحالات التالية:
      1. تجذب الأرض القمر،
      2. صبي يركل كرة قدم،
      3. صاروخ يتسارع إلى الأعلى،
      4. تتسارع السيارة إلى الأمام،
      5. قفزات عالية، و
      6. يتم إطلاق رصاصة من بندقية.
    2. افترض أنك تحمل فنجانًا من القهوة في يدك. حدد جميع القوى على الكأس ورد الفعل على كل قوة.
    3. (أ) لماذا ترتد البندقية العادية (تركل للخلف) عند إطلاقها؟ (ب) يكون ماسورة البندقية عديمة الارتداد مفتوحة من كلا الطرفين. وصف كيفية تطبيق قانون نيوتن الثالث عند إطلاق النار. (ج) هل يمكنك الوقوف بأمان بالقرب من إحداها عند إطلاقها؟

    5.6 القوى المشتركة

    1. يتم وضع طاولة على سجادة. ثم يتم وضع كتاب على الطاولة. على ماذا تؤثِّر الأرضية بقوة عادية؟
    2. يتحرك جسيم إلى اليمين. (أ) هل يمكن للقوة الموجودة عليها أن تعمل على اليسار؟ إذا كانت الإجابة بنعم، ماذا سيحدث؟ (ب) هل يمكن لهذه القوة أن تعمل نزولاً؟ إذا كانت الإجابة بنعم، لماذا؟

    5.7 رسم مخططات الجسم الحر

    1. عند إكمال حل مشكلة تتضمن القوى، ماذا نفعل بعد إنشاء مخطط الجسم الحر؟ وهذا هو، ماذا نطبق؟
    2. إذا كان الكتاب موجودًا على طاولة، فما عدد القوى التي يجب توضيحها في مخطط الجسم الحر للكتاب؟ قم بتوصيفها.
    3. إذا كان الكتاب في السؤال السابق في حالة سقوط حر، فما عدد القوى التي يجب أن تظهر في مخطط الجسم الحر للكتاب؟ قم بتوصيفها.

    مشاكل

    5.1 القوى

    1. يتم ربط حبلين بشجرة، ويتم تطبيق قوى\(\vec{F}_{1}\) = 2.0\(\hat{i}\) + 4.0\(\hat{j}\) N و\(\vec{F}_{2}\) = 3.0\(\hat{i}\) + 6.0\(\hat{j}\) N. القوى مستوية (في نفس المستوى). (أ) ما الناتج (القوة الصافية) لمتجه القوة هذين؟ (ب) أوجد مقدار واتجاه هذه القوة الصافية.
    2. يحتوي عمود الهاتف على ثلاثة كبلات تسحب كما هو موضح من الأعلى، مع\(\vec{F}_{1}\) = (\(\hat{i}\)300.0+ 500.0\(\hat{j}\))،\(\vec{F}_{2}\) = −200.0\(\hat{i}\)،\(\vec{F}_{3}\) و= −800.0\(\hat{j}\). (أ) أوجد القوة الصافية على عمود الهاتف في شكل مكون. (ب) أوجد مقدار واتجاه هذه القوة الصافية.

    يوضح الشكل محاور الإحداثيات، والمتجه F1 بزاوية تبلغ حوالي 28 درجة مع المحور y الموجب، والمتجه F2 على طول المحور x السالب، والمتجه F3 على طول المحور y السالب.

    1. يقوم مراهقان بسحب الحبال المرفقة بشجرة. الزاوية بين الحبال هي 30.0 درجة. يسحب ديفيد بقوة 400.0 نيوتن وتسحب ستيفاني بقوة 300.0 نيوتن. (أ) أوجد الشكل المكوِّن للقوة الصافية. (ب) أوجد مقدار القوة المحصلة (الشبكة) على الشجرة والزاوية التي تصنعها بحبل داود.

    5.2 قانون نيوتن الأول

    1. تؤثر قوتان\(\vec{F}_{1}\) = 75.0 2 (\(\hat{i}\)−\(\hat{j}\)) N و\(\vec{F}_{2}\) =\(\frac{150.0}{\sqrt{2}} (\hat{i} − \hat{j})\) N على جسم. أوجد القوة\(\vec{F}_{3}\) الثالثة اللازمة لموازنة القوتين الأوليين.
    2. أثناء انزلاق الأريكة على الأرض، تمارس أندريا وجينيفر\(\vec{F}_{A}\) قواهما\(\vec{F}_{J}\) على الأريكة. قوة أندريا متجهة شمالًا بقوة ١٣٠٫٠ نيوتن وقوة جينيفر ٣٢ درجة شرقًا شمالًا بقوة ١٨٠٫٠ نيوتن. (أ) أوجد القوة الكلية في شكل مكوِّن. (ب) أوجد مقدار القوة الصافية واتجاهها. (ج) إذا لم يوافق زملاء أندريا وجينيفر في المنزل، ديفيد وستيفاني، على هذه الخطوة وأرادوا منع نقلها، فما هي القوة المشتركة التي\(\vec{F}_{DS}\) ينبغي عليهم دفعها حتى لا تتحرك الأريكة؟

    5.3 قانون نيوتن الثاني

    1. يبدأ أندريا، العداء الذي يبلغ وزنه 63.0 كجم، سباقًا بتسارع 4.200 متر/ثانية 2. ما هي القوة الخارجية الصافية عليها؟
    2. إذا كانت العداءة الناتجة عن المشكلة السابقة تتسارع بهذا المعدل لمسافة ٢٠٫٠٠ م ثم حافظت على تلك السرعة للفترة المتبقية من مسافة ١٠٠٠٠ متر، فما الوقت الذي ستقضيه في السباق؟
    3. يدفع المُنظِّف عربة الغسيل التي تزن ٤٫٥٠ كجم بحيث يكون صافي القوة الخارجية عليها ٦٠٫٠ نيوتن. احسب مقدار تسارع عربته.
    4. يبدو أن رواد الفضاء في المدار يفتقرون إلى الوزن. هذا يعني أن هناك حاجة إلى طريقة ذكية لقياس كتلة رواد الفضاء لمراقبة مكاسبهم أو خسائرهم الجماعية وتعديل نظامهم الغذائي. تتمثل إحدى طرق القيام بذلك في ممارسة قوة معروفة على رائد فضاء وقياس التسارع الناتج. لنفترض أن قوة خارجية صافية مقدارها ٥٠٫٠ نيوتن قد تمت، وأن تسارع رائد الفضاء قد تم قياسه ليكون ٨٩٫٨٩٣ م/ث ٢. (أ) احسب كتلتها. (ب) من خلال ممارسة قوة على رائد الفضاء، تتعرض المركبة التي تدور فيها لقوة متساوية ومعاكسة. استخدم هذه المعرفة لإيجاد معادلة لتسريع النظام (رائد الفضاء وسفينة الفضاء) التي يمكن قياسها بواسطة مراقب قريب. (ج) مناقشة كيفية تأثير ذلك على قياس تسارع رائد الفضاء. اقترح طريقة يتم من خلالها تجنب ارتداد السيارة.
    5. في الشكل 5.4.3، تُعطى القوة الخارجية الصافية المؤثرة على جزازة وزنها ٢٤ كجم كما يساوي ٥١ نيوتن. إذا كانت قوة الاحتكاك المقابلة للحركة هي ٢٤ نيوتن، فما القوة F (بالنيوتون) التي يُمارس عليها الشخص على جزازة العشب؟ لنفترض أن الجزازة تتحرك بسرعة 1.5 متر/ثانية عند إزالة القوة F. إلى أي مدى ستذهب الجزازة قبل التوقف؟
    6. تتباطأ زلاجة الصاروخ الموضحة أدناه بمعدل 196 متر/ثانية 2. ما القوة اللازمة لإحداث هذا التباطؤ؟ افترض أن الصواريخ مطفأة. تبلغ كتلة النظام 2.10 × 10 3 كجم.

    يوضِّح الشكل زلاجة صاروخية تشير إلى اليمين. قوة الاحتكاك للنقاط المتبقية. القوة الصاعدة N والقوة الهبوطية w متساوية في الحجم.

    1. إذا كانت الزلاجة الصاروخية الموضحة في المشكلة السابقة تبدأ بحرق صاروخ واحد فقط، فما مقدار هذا التسارع؟ لنفترض أن كتلة النظام تساوي 2.10 × 3 كجم، وقوة الدفع T تساوي 2.40 × 10 4 نيوتن، وقوة الاحتكاك المقابلة للحركة هي 650.0 نيوتن. (ب) لماذا لا يمثل التسارع ربع ما يحدث مع احتراق جميع الصواريخ؟
    2. ما مقدار تباطؤ الزلاجة الصاروخية إذا استقرت بعد ١٫١٠ ث من سرعة ١٠٠٫٠ كم/س؟ (تسبب هذا التباطؤ في تعرض أحد الاختبارات لفقدان الوعي والعمى المؤقت.)
    3. لنفترض أن طفلين يدفعان أفقيًا، ولكن في اتجاهين متعاكسين تمامًا، على طفل ثالث في عربة. يُمارس الطفل الأول قوة مقدارها ٧٥٫٠ نيوتن، والثاني بقوة ٩٠٫٠ نيوتن، والاحتكاك ١٢,٠ نيوتن، وكتلة الطفل الثالث زائد العربة ٢٣٫٠ كجم. (أ) ما هو نظام الفائدة إذا أريد حساب تسارع الطفل في العربة؟ (انظر مخطط الجسم الحر.) (ب) حساب التسارع. (ج) ماذا سيكون التسارع إذا كان الاحتكاك يبلغ 15.0 نيوتن؟

    يوضح الشكل مخطط الجسم الحر. القوة: 4 نقاط لليمين، وأجبر نقاط N لأعلى، وأجبر Fu و f على الانتقال إلى اليسار، وأجبر w على الإشارة إلى الأسفل.

    1. يمكن لدراجة نارية قوية أن تنتج تسارعًا قدره 3.50 م/ث 2 أثناء السير بسرعة 90.0 كم/ساعة، وعند هذه السرعة، يبلغ إجمالي القوى المقاومة للحركة، بما في ذلك الاحتكاك ومقاومة الهواء، 400.0 نيوتن (مقاومة الهواء مماثلة للاحتكاك الهوائي. إنها تعارض دائمًا حركة الكائن.) ما مقدار القوة التي تؤثِّر بها الدراجة النارية للخلف على الأرض لإحداث التسارع إذا كانت كتلة الدراجة النارية التي كان راكبها ٢٤٥ كجم؟
    2. تسارع سيارة كتلتها ١٠٠٠٠ كجم من ٠ إلى ٩٠٫٠ كم/س خلال ١٠٫٠ ث. (أ) ما عجلتها؟ (ب) ما القوة الصافية المؤثِّرة على السيارة؟
    3. استخدم السائق في المشكلة السابقة المكابح عندما تتحرَّك السيارة بسرعة ٩٠٫٠ كم/س، وتستريح السيارة بعد قطعها مسافة ٤٠٫٠ مترًا، ما القوة الكلية المؤثِّرة على السيارة أثناء التباطؤ؟
    4. راكب وزنه 80.0 كجم في سيارة دفع رباعي يسافر بسرعة 1.00 × 10 2 كم/ساعة يرتدي حزام الأمان. يضغط السائق على المكابح وتتوقف السيارة الرياضية متعددة الاستخدامات على مسافة 45.0 مترًا، واكتشف قوة حزام الأمان على الراكب.
    5. جسم كتلته ٢٫٠ كجم تؤثِّر عليه قوة واحدة\(\vec{F}_{1}\) = ١٨\(\hat{i}\) نيوتن. (أ) ما مقدار تسارع الجسيم؟ (ب) إذا بدأ الجسيم في السكون، فما المسافة التي يقطعها في أول 5.0 ثوانٍ؟
    6. لنفترض أن جسيم المشكلة السابقة يواجه أيضًا قوى\(\vec{F}_{2}\) = −15\(\hat{i}\) نيوتن\(\vec{F}_{3}\) و= 6.0\(\hat{j}\) نيوتن. ما عجلته في هذه الحالة؟
    7. أوجد تسارع الجسم الذي كتلته ٥٫٠ كجم الموضَّح أدناه.

    يوضح الشكل دائرة تحمل العلامة m في المستوى xy. ثلاثة سهام تنبع منه. نقطة واحدة لليمين ويتم تصنيفها بـ 10 في نيوتن. بقيت نقاط أخرى وتم تصنيفها -2 في نيوتن. تشير النقطة الثالثة إلى الأسفل ويتم تصنيفها - 4 j نيوتن.

    1. في الشكل التالي، يكون السطح الأفقي الذي تنزلق عليه هذه الكتلة بدون احتكاك. إذا كان مقدار كل من القوتين المؤثرتين عليه F = 30.0 نيوتن وM = 10.0 كجم، فما مقدار التسارع الناتج للكتلة؟

    يوضح الشكل صندوقًا يحمل العلامة M يستقر على سطح. يُطلق على السهم الذي يشكل زاوية ناقص 30 درجة مع الأفقي علامة F ويشير إلى اتجاه المربع. يشير سهم آخر يحمل علامة F إلى اليمين.

    5.4 الكتلة والوزن

    1. يبلغ وزن رائد الفضاء بالإضافة إلى بدلته الفضائية على القمر 250 نيوتن فقط. (أ) كم يزن رائد الفضاء المناسب على الأرض؟ (ب) ما هي الكتلة على القمر؟ على الأرض؟
    2. لنفترض أن كتلة الوحدة المحملة بالكامل التي ينطلق منها رواد الفضاء من القمر هي 1.00 × 10 4 كجم. قوة دفع محركاتها هي 3.00 × 10 4 نيوتن. (أ) احسب مقدار تسارع الوحدة في الإقلاع الرأسي من القمر. (ب) هل يمكن أن تنطلق من الأرض؟ إذا لم يكن الأمر كذلك، فلماذا لا؟ إذا كان ذلك ممكنًا، فاحسب حجم التسارع.
    3. تتسارع زلاجة صاروخية بمعدل ٤٩٫٠ م/ث ٢. يبلغ وزن راكبها 75.0 كجم. (أ) احسب المكون الأفقي للقوة التي يمارسها المقعد على جسمه. قارن هذا بوزنه باستخدام النسبة. (ب) احسب اتجاه وحجم القوة الكلية التي يمارسها المقعد على جسمه.
    4. كرر المشكلة السابقة في حالة تتباطأ فيها زلاجة الصاروخ بمعدل 201 متر/ثانية 2. في هذه المشكلة، يتم التأثير على القوى بواسطة المقعد وحزام الأمان.
    5. دُفع جسم كتلته ٢٫٠٠ كجم لأعلى بشكل مستقيم بقوة رأسية مقدارها ٢٥٫٠ نيوتن. ما هو التسارع؟
    6. تبدأ سيارة وزنها ١٢٥٠٠ نيوتن من السكون وتتسارع إلى ٨٣٫٠ كم/س في ٥٫٠٠ ث، وتكون قوة الاحتكاك ١٣٥٠ نيوتن. أوجد القوة المُطبّقة التي يُنتجها المحرّك.
    7. يُفترَض وجود جسم كتلته ١٠٫٠ كجم في مجال جاذبية الأرض بمقدار g = ٩٫٨٠ م/ث ٢. ما القوة الكلية المؤثِّرة على الجسم إذا لم تكن هناك قوى خارجية أخرى تؤثِّر على الجسم؟
    8. كتلة رجل الإطفاء m؛ يسمع إنذار الحريق وينزلق لأسفل العمود بسرعة a (وهو أقل من g في الحجم). (أ) اكتب معادلة توضح القوة الرأسية التي يجب أن يطبقها على القطب. (ب) إذا كانت كتلته ٩٠٫٠ كجم وتسارع بسرعة ٥٫٠٠ م/ث ٢، فما مقدار قوته المُطبَّقة؟
    9. يقوم صائد البيسبول بأداء حيلة لإعلان تلفزيوني. سيلتقط كرة بيسبول (كتلتها ١٤٥ جم) سقطت من ارتفاع ٦٠٫٠ مترًا فوق قفازه. أوقف قفازه الكرة خلال ٠٫٠٫١ ث، ما القوة التي يؤثِّر بها القفاز على الكرة؟
    10. عندما يكون القمر فوق سطح القمر مباشرة عند غروب الشمس، تكون قوة الأرض على القمر، F EM، أساسًا عند 90 درجة مقابل قوة الشمس على القمر، F SM، كما هو موضح أدناه. إذا كانت F EM = 1.98 x 10 20 N وF SM = 4.36 x 10 20 N، فإن جميع القوى الأخرى على القمر ضئيلة، وكتلة القمر 7.35 x 10 22 kg، فأوجد مقدار تسارع القمر.

    يوضِّح الشكل دائرة تحمل اسم القمر. يُطلق على السهم الذي يشير إلى الأعلى اسم F subcept EM. سهم آخر منه يشير إلى اليمين يسمى F sumpict SM.

    ٥.٥ قانون نيوتن الثالث

    1. (أ) ما القوة الخارجية الصافية المؤثِّرة على قذيفة مدفعية وزنها 1100.0 كجم أُطلقت من سفينة حربية إذا تسارعت القذيفة بسرعة 2.40 x 10 4 م/ث 2؟ (ب) ما مقدار القوة التي تؤثر بها قذيفة المدفعية على السفينة، ولماذا؟
    2. يتم دفع لاعب الرجبي الشجاع ولكن غير الكافي إلى الوراء من قبل لاعب منافس يمارس قوة 800.0 N عليه. كتلة اللاعب الخاسر بالإضافة إلى المعدات هي 90.0 kg، وهو يتسارع للخلف بسرعة 1.20 m/s 2. (أ) ما هي قوة الاحتكاك بين أقدام اللاعب الخاسر والعشب؟ (ب) ما القوة التي يمارسها اللاعب الفائز على الأرض للمضي قدمًا إذا كانت كتلته زائد المعدات 110.0 كجم؟
    3. يوجد كتاب تاريخ فوق كتاب فيزياء على مكتب، كما هو موضح أدناه؛ كما يظهر رسم تخطيطي للجسم الحر. تزن كتب التاريخ والفيزياء 14 نيوتن و 18 نيوتن على التوالي. حدد كل قوة في كل كتاب باستخدام رمز منخفض مزدوج (على سبيل المثال، يمكن وصف قوة الاتصال لكتاب التاريخ التي تضغط على كتاب الفيزياء على أنها\(\vec{F}_{HP}\))، وحدد قيمة كل من هذه القوى، مع شرح العملية المستخدمة.

    يتم عرض مخططين مجانيين للجسم. يحتوي الأول على حرف F subcpt يشير لأعلى و F subcipt eh يشير إلى الأسفل. يحتوي الثاني على C subcipt يشير إلى الأعلى و C subcipt لأعلى و F subcupt p يشير لأسفل.

    1. تصطدم الشاحنة بسيارة، وأثناء التصادم، تكون القوة الصافية لكل مركبة هي في الأساس القوة التي تمارسها الأخرى. لنفترض أن كتلة السيارة 550 كجم، وكتلة الشاحنة 2200 كجم، وحجم تسارع الشاحنة هو 10 م/ث 2. أوجد مقدار تسارع السيارة.

    5.6 القوى المشتركة

    1. يتم تعليق الساق في نظام الجر، كما هو موضح أدناه. (أ) أي جزء من الشكل يُستخدم لحساب القوة المؤثِّرة على القدم؟ (ب) ما مقدار الشد في الحبل؟ هنا\(\vec{T}\) التوتر،\(\vec{w}_{leg}\) هو وزن الساق، ووزن\(\vec{w}\) الحمولة التي توفر التوتر.

    يوضح الشكل ساقًا على اليسار. يتم توصيله بحبل في الكاحل وتعليقه من بكرة في الأعلى. يستمر الحبل حتى يصل إلى بكرة ثانية على يمين الأولى، وثالثة إلى أسفل الثانية، ورابعة إلى أسفل يسار الثالثة، وخامس إلى أسفل يمين الرابعة. يتم تثبيت جسم وزنه w = mg في نهاية الحبل. يشير سهم مكتوب عليه ساق صغيرة إلى الأسفل من الكاحل وسهم يحمل علامة T يشير لأعلى من هناك. يُشكل سهم مُسمى T، من البكرة الرابعة إلى الثالثة، زاوية ثيتا بالأفقية. سهم آخر يسمى T، من البكرة الرابعة إلى الخامسة يشكل زاوية ناقص ثيتا مع الأفقي.

    1. لنفترض أن عظمة الظنبوب في الصورة السابقة كانت عظمة فخذ في منطقة جر لعظم مكسور، مع توفر البكرات والحبل. كيف يمكننا زيادة القوة على طول عظم الفخذ باستخدام نفس الوزن؟
    2. يقوم فريق مكون من تسعة أعضاء في مبنى طويل بشد خيط متصل بصخر كبير على سطح جليدي. كتلة الصخرة 200 كجم وتم سحبها بقوة 2350 نيوتن. (أ) ما مقدار العجلة؟ (ب) ما القوة المطلوبة لإنتاج سرعة ثابتة؟
    3. ما القوة التي يجب على الترامبولين تطبيقها على جينيفر، لاعبة الجمباز التي تزن ٤٥٫٠ كجم، لتسريع صعودها بشكل مستقيم بسرعة ٧٫٥٠ م/ث ٢؟ الإجابة مستقلة عن سرعة لاعبة الجمباز - يمكن أن تتحرك لأعلى أو لأسفل أو يمكن أن تكون ثابتة على الفور.
    4. (أ) احسب الشد في خيط عمودي من شبكة العنكبوت إذا كان عنكبوت كتلته 2.00 x 10 −5 kg معلَّقًا عليه بلا حراك. (ب) احسب الشد في خيط أفقي من شبكة العنكبوت إذا كان العنكبوت نفسه يجلس بلا حراك في منتصفه مثل المشاية ذات الحبل المشدود في الشكل 5.26. يتدلى الحبل بزاوية 12 درجة تحت الأفقي. قارن هذا بالتوتر في الخصلة الرأسية (ابحث عن نسبتها).
    5. لنفترض أن كيفن، وهو لاعب جمباز يبلغ وزنه 60 كجم، يتسلق حبلًا. (أ) ما مقدار الشد في الحبل إذا تسلق بسرعة ثابتة؟ (ب) ما مقدار الشد في الحبل إذا تسارع لأعلى بمعدل 1.50 م/ث 2؟
    6. أظهر، كما هو موضح في النص، أن القوة \(\perp\)F المؤثرة على وسيط مرن في وسطه وعموديًا على طوله (مثل على سلك الحبل المشدود في الشكل 5.26) تؤدي إلى توتر ذي حجم\(T = \frac{F_{\perp}}{2 \sin \theta}\).
    7. ضع في اعتبارك الشكل 5.28. يحاول السائق إخراج السيارة من الوحل عن طريق ممارسة قوة عمودية مقدارها 610.0 نيوتن، والمسافة التي تدفعها في منتصف الحبل هي 1.00 متر بينما تقف على بعد 6.00 متر من السيارة على اليسار و6.00 متر من الشجرة على اليمين. ما مقدار الشد T في الحبل، وكيف تجد الإجابة؟
    8. كتلة طائر 26 جرامًا ويجثم في منتصف خط هاتف ممتد. (أ) أظهر أن التوتر في الخط يمكن حسابه باستخدام المعادلة\(T = \frac{mg}{2 \sin \theta}\). حدد التوتر عندما (ب)\(\theta\) = 5 درجات و (ج)\(\theta\) = 0.5 درجة. افترض أن كل نصف من الخط مستقيم.

    يوضِّح الشكل طائرًا جالسًا على سلك مثبت في كلا الطرفين. يتدلى السلك بوزنه، مكونًا ثيتا الزاوية مع الوضع الأفقي على كلا الجانبين.

    1. أحد طرفي حبل طوله 30 مترًا مربوط بشجرة؛ والطرف الآخر مرتبط بسيارة عالقة في الطين. يسحب السائق جانبًا عند منتصف الحبل، ويخرجه لمسافة 2 متر، وإذا مارس قوة مقدارها ٨٠ نيوتن في ظل هذه الظروف، فأوجد القوة المؤثِّرة على السيارة.
    2. ضع في اعتبارك وزن الطفل في الشكل التالي. (أ) ما كتلة الرضيع والسلة إذا لوحظت قراءة مقياس مقدارها 55 نيوتن؟ (ب) ما هو الشد T 1 في الحبل الذي يربط الطفل بالميزان؟ (ج) ما مقدار الشد T 2 في السلك الذي يربط المقياس بالسقف، إذا كانت كتلة المقياس 0.500 كجم؟ (د) رسم الموقف، مع الإشارة إلى نظام الاهتمام المستخدم لحل كل جزء. كتل الحبال ضئيلة.

    يُظهر الشكل طفلًا في سلة متصلة بمقياس زنبركي، والذي بدوره يتم تثبيته من دعامة صلبة. يشير السهم T2 إلى الأسفل من الدعم. يشير سهم آخر T2 لأعلى من أعلى المقياس. يشير السهم T1 إلى الأسفل من أسفل المقياس. يشير سهم آخر T1 لأعلى من السلة. سهم W يشير لأسفل من السلة. يحتوي المقياس على علامات من 0 إلى 300 نيوتن.

    1. ما القوة التي يجب أن تؤثِّر على صندوق وزنه ١٠٠٫٠ كجم على مستوًى غير احتكاكي يميل على ٣٠ درجة ليؤدي إلى تسارع مقداره ٢٫٠ م/ث ٢ فوق المستوى؟

    يوضِّح الشكل كائنًا على منحدر مقداره ٣٠ درجة. يُطلق على السهم الذي يشير لأعلى وبالتوازي مع المنحدر اسم F.

    1. توجد كتلة بوزن 2.0 كجم على منحدر سلس تمامًا يصنع زاوية 30 درجة مع الأفقي. (أ) ما هو تسارع الكتلة أسفل المنحدر وقوة المنحدر على الكتلة؟ (ب) ما القوة التي تؤثر صعوداً وبالتوازي مع المنحدر والتي تسمح للكتلة بالتحرك بسرعة ثابتة؟

    5.7 رسم مخططات الجسم الحر

    1. كرة كتلتها م معلقة عند السكون، معلقة بخيط. (أ) رسم جميع القوى. (ب) ارسم مخطط الجسم الحر للكرة.
    2. تتحرَّك سيارة على طول طريق أفقي. ارسم مخططًا للجسم الحر؛ تأكد من تضمين احتكاك الطريق الذي يتعارض مع الحركة الأمامية للسيارة.
    3. يندفع عداء ضد المسار، كما هو موضح. (أ) توفير رسم تخطيطي للجسم الحر يوضح جميع القوى الموجودة على العداء. (تلميح: ضع كل القوى في مركز جسمه، وقم بتضمين وزنه.) (ب) أعط رسمًا بيانيًا منقحًا يوضح نموذج المكون x.

    تظهر صورة لرجل يركض نحو اليمين. يشير سهم يحمل علامة F لأعلى ولليمين من الأرض باتجاه قدمه.

    1. يتم تعليق إشارة المرور من الكابلات كما هو موضح. ارسم مخططًا للجسم الحر على مستوى إحداثي لهذه الحالة.

    يوضح الشكل إشارة مرور معلقة من كبل أفقي بواسطة ثلاثة كبلات أخرى، T1 وT2 وT3. يتدلى T1 لأسفل ولليمين لتكوين زاوية 41 درجة باستخدام الكبل الأفقي. يتدلى T2 لأسفل ولليسار، مما يجعل الزاوية 63 درجة باستخدام الكبل الأفقي. تلتقي هذه عند نقطة ويتدلى T3 عموديًا من هنا. يتم توصيل الضوء بـ T3. يُطلق على المتجه المتجه المتجه لأسفل من الضوء اسم w يساوي 200 نيوتن.

    مشاكل إضافية

    1. تُؤثِّر قوتان صغيرتان،\(\vec{F}_{1}\) = −2.40\(\hat{i}\) − 6.10t\(\hat{j}\) شمالًا،\(\vec{F}_{2}\) و= 8.50\(\hat{i}\) − 9.70\(\hat{j}\) نيوتن، على كويكب مارق بواسطة زوج من الجرارات الفضائية. (أ) أوجد القوة الصافية. (ب) ما مقدار القوة الصافية واتجاهها؟ (ج) إذا كانت كتلة الكويكب 125 كجم، فما التسارع الذي يشهده (في شكل متجه)؟ (د) ما هو حجم التسارع واتجاهه؟
    2. تؤثر قوتان بقوة ٢٥ و٤٥ نيوتن على جسم ما. تختلف اتجاهاتهم بمقدار 70 درجة. تبلغ قوة التسارع الناتج 10.0 م/ث 2. ما كتلة الجسم؟
    3. تعمل قوة مقدارها 1600 نيوتن بالتوازي مع منحدر لدفع بيانو وزنه 300 كجم إلى شاحنة متحركة. المنحدر يميل عند 20 درجة. (أ) ما هو تسارع البيانو إلى أعلى المنحدر؟ (ب) ما سرعة البيانو عندما يصل إلى القمة إذا كان المنحدر يبلغ طوله 4.0 أمتار ويبدأ البيانو من السكون؟
    4. ارسم مخططًا للجسم الحر للغواص الذي دخل الماء وتحرك نحو الأسفل وتتأثر بقوة تصاعدية بسبب الماء الذي يوازن الوزن (أي أن الغواص معلق).
    5. بالنسبة للسباح الذي قفز للتو من على لوح الغوص، افترض أن مقاومة الهواء ضئيلة. كتلة السباح 80.0 كجم ويقفز من على لوح بارتفاع 10.0 متر فوق الماء. بعد ثلاث ثوان من دخول الماء، توقفت حركتها الهابطة. ما متوسط القوة التصاعدية التي مارسها الماء عليها؟
    6. (أ) أوجد معادلة لتحديد مقدار القوة الكلية المطلوبة لإيقاف سيارة كتلتها م، علمًا بأن السرعة الأولية للسيارة هي v 0 ومسافة التوقف هي x. (ب) أوجد مقدار القوة الصافية إذا كانت كتلة السيارة 1050 كجم، والسرعة الأولية 40.0 كم/ساعة، ونقطة التوقف المسافة هي 25.0 م.
    7. كتلة مركب شراعي 1.50 × 10 3 كجم وتؤثر عليه قوة مقدارها 2.00 × 10 3 نيوتن باتجاه الشرق، بينما تعمل الرياح خلف الأشرعة بقوة 3.00 × 10 3 نيوتن في اتجاه 45° شمال الشرق. أوجد مقدار واتجاه التسارع الناتج.
    8. أوجد تسارع الجسم الذي كتلته ١٠٫٠ كجم الموضَّح أدناه.

    تشع ثلاثة أسهم إلى الخارج من دائرة تسمى m. F1، تساوي 10 نيوتن، وتشير عموديًا لأسفل. يشير F2، الذي يساوي 20 نيوتن، لأعلى ولليمين، مما يجعل زاوية ناقص 37 درجة بمحور y الموجب. يشير F3، الذي يساوي 10 نيوتن، إلى الأعلى واليسار، ويصنع زاوية قدرها 37 درجة بمحور y الموجب.

    1. يتحرك جسم كتلته ٢٫٠ كجم على طول المحور السيني بسرعة ٣٫٠ م/ث في اللحظة المُمثَّلة أدناه. (أ) ما هو تسارع الجسم؟ (ب) ما سرعة الجسم بعد 10.0 ثانية؟ (ج) ما هي إزاحتها بعد 10.0 ثوان؟

    تشع ثلاثة أسهم إلى الخارج من دائرة تسمى m. F1، تساوي 50 نيوتن، وتشير لأعلى ولليمين، فتكون الزاوية 37 درجة باستخدام المحور x. يشير F2، الذي يساوي 30 نيوتن، إلى اليسار وإلى الأسفل، مما يجعل زاوية ناقص 30 درجة مع محور y السالب. يشير F3، الذي يساوي 80 نيوتن، إلى اليسار.

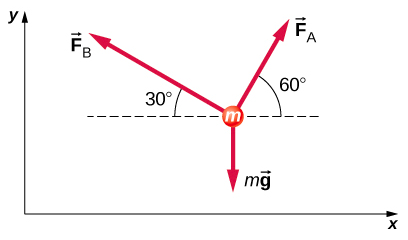
    1. القوة\(\vec{F}_{B}\) لديها ضعف حجم القوة\(\vec{F}_{A}\). أوجد الاتجاه الذي تتسارع فيه الجُسيم في هذا الشكل.

    يشع سهمان إلى الخارج من دائرة تسمى m. F. يشير الحرف A إلى اليمين. يشير F conpt B إلى الأسفل واليسار، مما يجعل الزاوية 45 درجة مع الأفقي.

    1. يوضِّح أدناه جسم كتلته ١٫٠ كجم تحت تأثير القوى\(\vec{F}_{A}\)\(\vec{F}_{B}\)، وm\(\vec{g}\). إذا تسارع الجسم إلى اليسار بسرعة ٢٠ م/ث ٢، فما القيمة\(\vec{F}_{A}\) و\(\vec{F}_{B}\)؟

    تشع ثلاثة سهام إلى الخارج من نقطة تسمى m F. يشير الحرف A إلى اليسار وإلى الأسفل، مما يجعل الزاوية 60 درجة مع محور x السالب. يشير F إلى اليسار وإلى الأعلى، مما يجعل زاوية ناقص 30 درجة مع محور x السالب. يشير المتجه mg عموديًا لأسفل.

    1. تؤثِّر قوة على سيارة كتلتها م بحيث تزداد السرعة v للسيارة مع الموضع x كـ v = kx 2، حيث تكون k ثابتة وتكون جميع الكميات بوحدات SI. أوجد القوة المؤثرة على السيارة كدالة للموضع.
    2. يتم تطبيق قوة 7.0-N موازية للانحدار على قفص وزنه 1.0 كجم. المنحدر مائل عند 20 درجة وهو غير قابل للاحتكاك. (أ) ما هو تسارع الصندوق؟ (ب) إذا كانت جميع الظروف الأخرى متماثلة ولكن قوة احتكاك المنحدر تبلغ 1.9 نيوتن، فما مقدار التسارع؟
    3. صندوقان، A و B، في حالة راحة. يقع الصندوق A على أرض مستوية، بينما يرتكز المربع B على مستوى مائل\(\theta\) بزاوية أفقية. (أ) اكتب تعبيرات القوة العادية المؤثرة على كل كتلة. (ب) قارن بين القوتين؛ أي حدد أيهما أكبر أو ما إذا كانت متساوية في الحجم. (ج) إذا كانت زاوية الميل ١٠ درجات، فما القوة الأكبر؟
    4. كتلة مقدارها 250.0 جم مُعلَّقة من زنبرك مُعلَّق رأسيًّا. يمتد الربيع 6.00 سم. ما مقدار تمدد الزنبرك إذا كانت الكتلة العالقة 530.0 جم؟
    5. كما هو موضح أدناه، يدعم زنبرك متطابقان، كل منهما ثابت زنبركي 20 نيوتن/متر، وزنًا يبلغ 15.0-نيوتن. (أ) ما هو التوتر في الربيع A؟ (ب) ما مقدار امتداد الزنبرك A من موضع الراحة؟

    يوضح الشكل نوابض متطابقة معلقة جنبًا إلى جنب. يتم تجميع أطرافها السفلية معًا لدعم الوزن. يصنع كل زنبرك زاوية 30 درجة مع الوضع الرأسي.

    1. يظهر أدناه كتلة وزنها 30.0 كجم ترتكز على منحدر غير احتكاكي يميل بزاوية 60 درجة إلى الأفقي. يتم تثبيت الكتلة بواسطة زنبرك ممتد 5.0 سم. ما ثابت قوة الزنبرك؟

    يوضِّح الشكل سطحًا مائلًا لأسفل ولليسار، مما يجعل الزاوية 60 درجة باستخدام الأفقي. جسم وزنه ٣٠ كجم يتدلى من زنبرك ويستقر على المنحدر.

    1. في بناء منزل، يستخدم النجارون المسامير من صندوق كبير. يتم تعليق الصندوق من الزنبرك مرتين خلال اليوم لقياس استخدام الأظافر. في بداية اليوم، يمتد الربيع 50 سم. في نهاية اليوم، يمتد الربيع 30 سم. ما الكسر أو النسبة المئوية من الأظافر التي تم استخدامها؟
    2. يتم تطبيق قوة على كتلة لتحريكها لأعلى بزاوية 30 درجة. المنحدر غير قابل للاحتكاك. إذا كانت F = 65.0 نيوتن وM = 5.00 كجم، فما مقدار تسارع الكتلة؟

    يوضِّح الشكل سطحًا مائلًا لأسفل ولليمينًا، ويصنع الزاوية الأفقية بزاوية مقدارها 30 درجة. يرتكز عليه صندوق يحمل علامة M. يشير سهم يحمل علامة F أفقيًا إلى اليسار باتجاه المربع. الزاوية التي يتكون منها السهم والمنحدر هي 30 درجة.

    1. تُطبّق قوتان على جسم وزنه ٥ كجم، وتتسارع بسرعة ٢٫٠ م/ث ٢ في الاتجاه الصادي الموجب. إذا كانت إحدى القوى تؤثِّر في الاتجاه السيني الموجب بمقدار 12.0 نيوتن، فأوجد مقدار القوة الأخرى.
    2. الكتلة الموجودة على اليمين الموضحة أدناه لها كتلة أكبر من الكتلة الموجودة على اليسار (m 2> m 1). ارسم مخططات للجسم الحر لكل كتلة.

    يتم توصيل بكرة بالسقف. يمر حبل فوقه. يتم توصيل كتلة كتلتها m1 بالطرف الأيسر من الحبل وكتلة أخرى تحمل علامة m2 متصلة بالطرف الأيمن من الحبل. M2 معلق بدرجة أقل من m1.

    مشاكل التحدي

    1. في حالة سحب قاطرتين على سفينة معطلة، كما هو موضح هنا في المنظر العلوي، سيتم سحب السفينة المعطلة على طول الاتجاه المشار إليه بنتيجة القوى المستخدمة. (أ) رسم مخطط للجسم الحر للسفينة. افترض عدم تأثير قوى الاحتكاك أو السحب على السفينة. (ب) هل قمت بتضمين جميع القوى في المنظر العلوي في مخطط الجسم الحر الخاص بك؟ لماذا أو لماذا لا؟

    يوضِّح الشكل المنظر العلوي لقاطرتين تسحبان سفينة معطلة إلى اليسار. يقع Arrow F1 على طول الخط الذي يربط السفينة بالقاطرة العلوية. يقع السهم F2 على طول الخط الذي يربط السفينة بالقاطرة السفلية. F1 أطول من F2. يُظهر السهم F مخطوطة R القوة المجمعة. يقع بين F1 و F2، ويشير إلى اليسار وإلى الأعلى قليلاً.

    1. يتحرَّك جسم وزنه ١٠٫٠ كجم في البداية شرقًا بسرعة ١٥٫٠ م/ث، ثم تؤثِّر عليه قوة لمدة ٢٫٠٠ ثانية، ثم تتحرَّك بعد ذلك نحو الشمال الغربي بسرعة ١٥٫٠ م/ث أيضًا. ما مقدار واتجاه القوة المتوسطة التي تؤثِّر على الجسم خلال فترة ٢٫٠٠ ثانية؟
    2. في 25 يونيو 1983، قام مضرب الرماية أودو باير من ألمانيا الشرقية بإلقاء الطلقة التي يبلغ وزنها 7.26 كجم على ارتفاع 22.22 مترًا، والتي كانت في ذلك الوقت رقمًا قياسيًا عالميًا. (أ) إذا أُطلقت الطلقة على ارتفاع 2.20 مترًا بزاوية إسقاط مقدارها 45.0 درجة، فما سرعتها الأولية؟ (ب) إذا كانت الطلقة في يد باير قد تسارعت بشكل منتظم على مسافة ١٫٢٠ م، فما القوة الصافية المؤثِّرة عليها؟
    3. يتحرك جسم كتلته m في اتجاه أفقي بحيث يُعطى موضعه في الوقت المناسب x (t) = عند 4+ bt 3+ ct، حيث تكون a و b و c ثوابت. (أ) ما هو تسارع الجسم؟ (ب) ما هي القوة المعتمدة على الوقت التي تؤثر على الجسم؟
    4. جسم كتلته m سرعته الأولية v 0 في الاتجاه السيني الموجب. يتم التأثير عليها بقوة ثابتة F للوقت t حتى تصبح السرعة صفرًا؛ تستمر القوة في التأثير على الجسم حتى تصبح سرعته −v 0 في نفس الفترة الزمنية. اكتب مقدارًا يُعبِّر عن المسافة الكلية التي يقطعها الجسم بدلالة المتغيرات المشار إليها.
    5. تبلغ سرعات جسم وزنه 3.0 كجم عند t = 6.0 ثانية و t = 8.0 ثانية (3.0\(\hat{i}\) − 6.0\(\hat{j}\) + 4.0\(\hat{k}\)) م/ث و (−2.0\(\hat{i}\) + 4.0\(\hat{k}\)) م/ث، على التوالي. إذا كان الجسم يتحرَّك بسرعة ثابتة، فما القوة المؤثِّرة عليه؟
    6. رائد فضاء وزنه 120 كجم يركب زلاجة صاروخية تنزلق على طول طائرة مائلة. تحتوي الزلاجة على مكون أفقي للتسارع يبلغ 5.0 م/ث 2 ومكون هبوطي قدره 3.8 م/ث 2. احسب مقدار القوة المؤثِّرة على الراكب بواسطة الزلاجة. (تلميح: تذكر أنه يجب مراعاة تسارع الجاذبية.)
    7. تؤثِّر قوَّتان على جسم وزنه 5.0 كجم يتحرَّك بسرعة 2.0 م/ث 2 في الاتجاه الصادي الموجب. إذا كانت إحدى القوى تؤثِّر في الاتجاه السيني الموجب ومقدارها 12 نيوتن، فما مقدار القوة الأخرى؟
    8. لنفترض أنك تشاهد لعبة كرة قدم من طائرة هليكوبتر فوق الملعب. يقوم لاعبان من لاعبي كرة القدم في نفس الوقت بركل كرة قدم ثابتة في الملعب المسطح؛ كتلة كرة القدم 0.420 كجم. يركل اللاعب الأول بقوة 162 نيوتن عند 9.0° شمال الغرب. في نفس اللحظة، يركل اللاعب الثاني بقوة 215 نيوتن عند 15 درجة شرق الجنوب. أوجد تسارع الكرة في\(\hat{i}\)\(\hat{j}\) الشكل.
    9. كتلة مقدارها ١٠,٠ كجم معلقة من زنبرك ثابت زنبركي يبلغ ٥٣٥ نيوتن/م، أوجد موضع نهاية الزنبرك بعيدًا عن موضع السكون. (استخدم g = 9.80 م/ث 2.)
    10. يتم توصيل زوج من النرد الضبابي وزنه 0.0502 كجم بمرآة الرؤية الخلفية للسيارة بخيط قصير. تتسارع السيارة بمعدل ثابت، ويتدلى النرد بزاوية 3.20 درجة من العمودي بسبب تسارع السيارة. ما مقدار تسارع السيارة؟
    11. في السيرك، يسحب حمار زلاجة تحمل مهرجًا صغيرًا بقوة مقدارها 2.48\(\hat{i}\) + 4.33\(\hat{j}\) نيوتن. يسحب حصان على نفس الزلاجة لمساعدة الحمار التعيس بقوة 6.56\(\hat{i}\) + 5.33\(\hat{j}\) نيوتن وكتلة الزلاجة 575 كجم. باستخدام\(\hat{j}\) الشكل\(\hat{i}\) والصورة للإجابة على كل مسألة، أوجد (أ) القوة الكلية المؤثِّرة على الزلاجة عندما يعمل الحيوانان معًا، (ب) تسارع الزلاجة، (ج) السرعة بعد ٦٫٥٠ ثانية.
    12. يتدلى من السقف فوق سرير الأطفال، بعيدًا عن متناول الطفل، خيط بأشكال بلاستيكية، كما هو موضح هنا. الخيط مشدود (لا يوجد ارتخاء)، كما هو موضح في الأجزاء المستقيمة. كل شكل بلاستيكي له نفس الكتلة m، ويتباعد بينهما بالتساوي بمسافة d، كما هو موضح. \(\theta\)تصف الزوايا المُصنَّفة الزاوية المتكونة من نهاية الخيط والسقف عند كل طرف. طول مركز اللدغة أفقي. يشكل كل من المقطعين المتبقيين زاوية مع وضع علامة أفقية\(\phi\). دع T 1 يكون الشد في القسم الأيسر من السلسلة، ويكون T 2 هو التوتر في القسم المجاور له، و T 3 هو التوتر في الجزء الأفقي. (أ) ابحث عن معادلة الشد في كل قسم من السلسلة بدلالة المتغيرات m و g و\(\theta\). (ب) أوجد الزاوية\(\phi\) بدلالة الزاوية\(\theta\). (ج) إذا كان\(\theta\) = 5.10 درجة، فما قيمة\(\phi\)؟ (د) أوجد المسافة x بين نقاط النهاية بدلالة d و\(\theta\).

    يوضح الشكل أربعة أشكال معلقة على خيط متصل بالسقف عند كلا الطرفين. تقسم الأشكال السلسلة إلى خمسة مقاطع متساوية، طول كل منها d. الجزء الأوسط أفقي. المسافة بين طرفي الخيط هي x. الزوايا بين السقف والأجزاء الأقرب إلى السقف تسمى theta. تم تصنيف الزوايا التي تشكلت من الأجزاء الأولى من السقف مع الأجزاء المجاورة لها على حد سواء phi.

    1. رصاصة تُطلق من بندقية كتلتها ١٠٫٠ جم وتنتقل إلى اليمين بسرعة ٣٥٠ م/ث، وتصطدم بهدف، وهو كيس رمل كبير، وتخترقه مسافة ٣٤٫٠ سم. أوجد مقدار واتجاه قوة التثبيط التي تبطئ الرصاصة وتوقفها.
    2. تؤثر على جسم ثلاث قوى متزامنة:\(\vec{F}_{1}\) =( −3.00\(\hat{i}\) + 2.00\(\hat{j}\)) N،\(\vec{F}_{2}\) = (6.00\(\hat{i}\) − 4.00\(\hat{i}\)) N،\(\vec{F}_{3}\) = (2.00\(\hat{i}\) + 5.00\(\hat{i}\)) N. يواجه الجسم تسارعًا مقداره 4.23 م/ث 2. (أ) أوجد متجه التسارع بدلالة m. (ب) أوجد كتلة الجسم. (ج) إذا بدأ الجسم من السكون، فأوجد سرعته بعد الساعة ٥٫٠٠ ث. (د) أوجد مكونات سرعة الجسم بعد ٥٫٠٠ ث.
    3. في مسرّع جسيمات، كتلته ١٫٦٧ × ١٠ −٢٧ كجم، وسرعته الأولية ٢٫٠٠ × ١٠ ٥ م/ث، ويتحرَّك في خط مستقيم، وترتفع سرعته إلى ٩٫٠٠ × ١٠ ٥ م/ث على مسافة ١٠٫٠ سم. افترض أن التسارع ثابت. أوجد مقدار القوة المؤثِّرة على البروتون.
    4. يتم توجيه طائرة بدون طيار عبر بحيرة مغطاة بالجليد بدون احتكاك. تبلغ كتلة الطائرة بدون طيار 1.50 kg، وسرعتها 3.00\(\hat{i}\) m/s، وبعد 10.0 ثانية، تصبح السرعة\(\hat{i}\) 9.00+ 4.00\(\hat{j}\) m/s، وإذا كانت هناك قوة ثابتة في الاتجاه الأفقي تسبب هذا التغيير في الحركة، فأوجد (أ) مكونات القوة و (ب) مقدار القوة.

    المساهمون والصفات

    Template:ContribOpenStaxUni