Skip to main content
Global

5.8: رسم مخططات الجسم الحر

  1. Last updated
  2. Save as PDF
  • Page ID
    200094

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم
    • اشرح قواعد رسم مخطط الجسم الحر
    • قم بإنشاء مخططات للجسم الحر لمواقف مختلفة

    تتضمن الخطوة الأولى في وصف وتحليل معظم الظواهر في الفيزياء الرسم الدقيق لمخطط الجسم الحر. تم استخدام مخططات الجسم الحر في أمثلة طوال هذا الفصل. تذكر أن مخطط الجسم الحر يجب أن يتضمن فقط القوى الخارجية التي تعمل على الجسم المعني. بمجرد رسم مخطط دقيق للجسم الحر، يمكننا تطبيق قانون نيوتن الأول إذا كان الجسم في حالة توازن (قوى متوازنة؛ أي\(F_{net} = 0\)) أو قانون نيوتن الثاني إذا كان الجسم يتسارع (القوة غير المتوازنة؛ أي\(F_{net} \neq 0\)).

    في Forces، قدمنا إستراتيجية مختصرة لحل المشكلات لمساعدتك على فهم مخططات الجسم الحر. هنا، نضيف بعض التفاصيل إلى الاستراتيجية التي ستساعدك في إنشاء هذه الرسوم البيانية.

    إستراتيجية حل المشكلات: إنشاء مخططات الجسم الحر

    يجب مراعاة القواعد التالية عند إنشاء مخطط الجسم الحر:

    1. ارسم الكائن قيد النظر؛ لا يجب أن يكون فنيًا. في البداية، قد ترغب في رسم دائرة حول الكائن محل الاهتمام للتأكد من التركيز على تصنيف القوى المؤثرة على الكائن. إذا كنت تتعامل مع الكائن كجسيم (بدون حجم أو شكل ولا دوران)، فقم بتمثيل الكائن كنقطة. غالبًا ما نضع هذه النقطة في أصل نظام الإحداثيات السينية.
    2. قم بتضمين جميع القوى التي تؤثر على الكائن، والتي تمثل هذه القوى في صورة متجهات. ضع في اعتبارك أنواع القوى الموصوفة في القوات المشتركة - القوة العادية والاحتكاك والتوتر وقوة الزنبرك - بالإضافة إلى الوزن والقوة المطبقة. لا تقم بتضمين القوة الصافية على الكائن. باستثناء الجاذبية، تتطلب جميع القوى التي ناقشناها اتصالًا مباشرًا بالجسم. ومع ذلك، يجب عدم تضمين القوى التي يمارسها الكائن على بيئته. لا نقوم أبدًا بتضمين كلتا قوتي زوج الحركة والتفاعل.
    3. قم بتحويل مخطط الجسم الحر إلى مخطط أكثر تفصيلاً يوضح مكونات x- و y لقوة معينة (غالبًا ما يكون هذا مفيدًا عند حل مشكلة باستخدام قانون نيوتن الأول أو الثاني). في هذه الحالة، ضع خطًا متعربًا عبر المتجه الأصلي لإظهار أنه لم يعد قيد التشغيل - فقد تم استبداله بمكوني x- و y.
    4. إذا كان هناك كائنان أو أكثر، أو جسدان، في المشكلة، ارسم مخططًا منفصلاً للجسم الحر لكل كائن.

    ملاحظة: إذا كان هناك تسارع، فإننا لا ندرجه مباشرة في مخطط الجسم الحر؛ ومع ذلك، قد يكون من المفيد الإشارة إلى التسارع خارج مخطط الجسم الحر. يمكنك تسميته بلون مختلف للإشارة إلى أنه منفصل عن مخطط الجسم الحر.

    دعونا نطبق استراتيجية حل المشكلات في رسم مخطط الجسم الحر للزلاجة. في الشكل\(\PageIndex{1a}\)، يتم سحب الزلاجة بالقوة\(\vec{P}\) بزاوية 30 درجة. في الجزء (ب)، نعرض مخططًا للجسم الحر لهذا الموقف، كما هو موضح في الخطوتين 1 و 2 من استراتيجية حل المشكلات. في الجزء (ج)، نعرض جميع القوى من حيث مكوناتها x- و y، بما يتماشى مع الخطوة 3.

    يوضح الشكل أ زلاجة وزنها 15 كجم. يشكل السهم المسمى P الذي يشير إلى اليمين وللأعلى زاوية مقدارها 30 درجة مع الأفقي. الشكل ب عبارة عن مخطط حر للجسم مع إشارة P و N لأعلى و w تشير إلى الأسفل. الشكل c عبارة عن مخطط مجاني للجسم يحتوي على P و N و w ومكونين من P: Px يشير إلى اليمين ويشير Py لأعلى.
    الشكل\(\PageIndex{1}\): (أ) تظهر الزلاجة المتحركة على شكل (ب) مخطط الجسم الحر و (ج) مخطط الجسم الحر بمكونات القوة.
    مثال\(\PageIndex{1}\): Two Blocks on an Inclined Plane

    قم بإنشاء مخطط الجسم الحر للكائن A والكائن B في الشكل\(\PageIndex{1}\).

    إستراتيجية

    نحن نتبع الخطوات الأربع المدرجة في استراتيجية حل المشكلات.

    الحل

    نبدأ بإنشاء رسم تخطيطي لأول كائن مهم. في الشكل\(\PageIndex{2a}\)، الكائن A معزول (محاط بدائرة) ويتم تمثيله بنقطة.

    يوضِّح الشكل أ جسمين على مستوًى مائل ينحدران إلى اليسار. يوجد الكائن A فوق الجسم B. يُظهر مخطط الجسم الحر T يشير إلى اليمين وإلى الأعلى، بالتوازي مع المستوى، N copuncept BA يشير إلى اليسار وإلى الأعلى، عموديًا على المستوى، إذا كان الرمز BA يشير إلى اليسار وإلى الأسفل، موازيًا للمستوى، ونحن نسقط A يشير عموديًا لأسفل. W p p هو وزن الكتلة A، T هو الشد، N منخفض BA هو القوة العادية التي يمارسها B على A، إذا كان الحد الأدنى BA هو قوة الاحتكاك التي يمارسها B على A. يوضح الشكل B الأجسام الموجودة على المنحدر بنفس الطريقة. يحتوي مخطط الجسم الحر على منخفض B و F يشير إلى اليمين وإلى الأعلى، موازيًا للمنحدر، N منخفض B يشير إلى اليسار وإلى الأعلى عموديًا على المنحدر، ث منخفض B يشير عموديًا لأسفل و N منخفض AB يشير لأسفل واليمين، عموديًا على المنحدر. W. الحد B هو وزن الكتلة B، N منخفض AB هو القوة العادية التي يمارسها A على B، N. منخفض B هو القوة الطبيعية التي يمارسها المستوى المنحدر على B. إذا كان المقطع AB هو قوة احتكاك يمارسها A على B. إذا كان المنحدر B هو قوة احتكاك يمارسها المستوى المائل على B.
    الشكل\(\PageIndex{2}\): (أ) مخطط الجسم الحر للجسم المعزول A. (ب) مخطط الجسم الحر للجسم المعزول B. بمقارنة الرسمتين، نرى أن الاحتكاك يعمل في الاتجاه المعاكس في الشكلين. نظرًا لأن الجسم A يواجه قوة تميل إلى سحبه إلى اليمين، يجب أن يعمل الاحتكاك على اليسار. نظرًا لأن الجسم B يواجه أحد مكونات وزنه الذي يسحبه إلى اليسار، إلى أسفل المنحدر، يجب أن تتصدى قوة الاحتكاك له وتعمل صعودًا على المنحدر. يعمل الاحتكاك دائمًا عكس الاتجاه المقصود للحركة.

    نقوم الآن بتضمين أي قوة تعمل على الجسم. هنا، لا توجد قوة مطبقة. يعمل وزن الجسم كقوة تشير عموديًا لأسفل، ويشير وجود السلك إلى قوة شد تتجه بعيدًا عن الجسم. يحتوي الكائن A على واجهة واحدة وبالتالي يواجه قوة عادية موجهة بعيدًا عن الواجهة. مصدر هذه القوة هو الكائن B، ويتم تصنيف هذه القوة العادية وفقًا لذلك. نظرًا لأن الكائن B يميل إلى الانزلاق لأسفل، فإن الكائن A يميل إلى الانزلاق لأعلى فيما يتعلق بالواجهة، لذلك يتم توجيه احتكاك BA لأسفل بالتوازي مع المستوى المائل.

    كما هو موضح في الخطوة 4 من إستراتيجية حل المشكلات، نقوم بعد ذلك ببناء مخطط الجسم الحر في الشكل 5.32 (ب) باستخدام نفس النهج. يواجه الكائن B قوتين عاديتين وقوتي احتكاك بسبب وجود سطحين ملامسان. تمارس الواجهة مع المستوى المائل قوى خارجية لـ N B و f B، وتمارس الواجهة مع الكائن B القوة العادية N AB والاحتكاك f AB؛ يتم توجيه N AB بعيدًا عن الكائن B، و f AB تعارض ميل الحركة النسبية للكائن B فيما يتعلق بالكائن A.

    الأهمية

    الكائن قيد النظر في كل جزء من هذه المشكلة مُحاط بدائرة باللون الرمادي. عندما تتعلم لأول مرة كيفية رسم مخططات الجسم الحر، ستجد أنه من المفيد وضع دائرة حول الكائن قبل تحديد القوى التي تؤثر على هذا الكائن المحدد. هذا يركز انتباهك ويمنعك من التفكير في القوى التي لا تعمل على الجسم

    مثال\(\PageIndex{2}\): Two Blocks in Contact

    يتم تطبيق القوة على كتلتين في حالة تلامس، كما هو موضح.

    إستراتيجية

    ارسم مخططًا للجسم الحر لكل كتلة. تأكد من مراعاة قانون نيوتن الثالث في الواجهة حيث تتلامس الكتلتين.

    يظهر مربعان في اتصال مع بعضهما البعض. الجزء الأيسر أصغر ويحمل اسم m1. الحجم الصحيح أكبر ويحمل علامة m2. يُطلق على السهم الذي يشير يمينًا نحو m1 اسم F.

    الحل

    يوضح الشكل رسمين تخطيطيين للجسم الحر. يُظهر الأول السهم A والسيناريو 21 الذي يشير إلى اليسار والسهم F الذي يشير إلى اليمين. يُظهر الثاني السهم A 12 الذي يشير إلى اليمين. يحتوي كلا المخططين أيضًا على أسهم تشير لأعلى ولأسفل.

    الأهمية

    \(\vec{A}_{21}\)هي قوة عمل الكتلة 2 على الكتلة 1. \(\vec{A}_{12}\)هي قوة رد فعل الكتلة 1 على الكتلة 2. نستخدم مخططات الجسم الحر هذه في تطبيقات قوانين نيوتن.

    مثال\(\PageIndex{3}\): Block on the Table (Coupled Blocks)

    توجد كتلة على الطاولة، كما هو موضح. يتم توصيل حبل خفيف به ويمر فوق بكرة. يتم ربط الطرف الآخر من الحبل بكتلة ثانية. ويقال أن الكتلتين مقترنتان. وتمارس الكتلة m 2 قوة بسبب وزنها، مما يؤدي إلى تسريع النظام (كتلتان وسلسلة).

    إستراتيجية

    نفترض أن السلسلة ليس لها كتلة حتى لا نضطر إلى اعتبارها كائنًا منفصلاً. ارسم مخططًا للجسم الحر لكل كتلة.

    يوضح الشكل الكتلة m1 الموضوعة على الطاولة. يمر خيط متصل بها فوق بكرة وأسفل الجانب الأيمن من الطاولة. تم تعليق كتلة m2 منه. يشير السهم a1 إلى اليمين ويشير السهم a2 إلى الأسفل.

    الحل

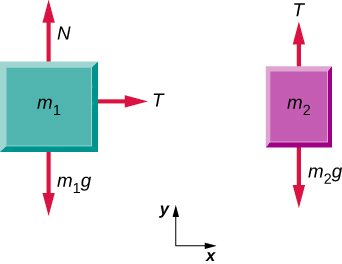
    يعرض الشكل أ الكتلة m1. يشير السهم المسمى N إلى الأعلى منه، ويشير السهم m1g إلى الأسفل، ويشير السهم T إلى اليمين. يوضح الشكل (ب) الكتلة m2. يشير سهم T لأعلى منه ويشير سهم m2g إلى الأسفل.

    الأهمية

    تتسارع كل كتلة (لاحظ الملصقات الموضحة لـ\(\vec{a}_{1}\) و\(\vec{a}_{2}\))؛ ومع ذلك، بافتراض بقاء الخيط مشدودًا، فإنها تتسارع بنفس المعدل. وبالتالي، لدينا |\(\vec{a}_{1}\) | = |\(\vec{a}_{2}\) |. إذا أردنا الاستمرار في حل المشكلة، يمكننا ببساطة الاتصال بالتسارع\(\vec{a}\). نستخدم أيضًا رسمين تخطيطيين للجسم الحر لأننا عادةً ما نجد الشد T، والذي قد يتطلب منا استخدام نظام من معادلتين في هذا النوع من المسائل. التوتر هو نفسه على كل من m 1 و m 2.

    التمارين الرياضية\(\PageIndex{1}\)
    1. ارسم مخطط الجسم الحر للحالة المعروضة.
    2. أعد رسمه لإظهار المكونات؛ استخدم محاور x موازية للمنحدرين.

    يتم ربط عربتين بحبل يمر فوق بكرة فوق تل. تقع كل عربة على منحدر واحد من التل على جانبي البكرة. عربة التسوق الموجودة على اليسار تحمل اسم m1 والعربة الموجودة على اليمين تسمى m2.

    محاكاة

    شاهد هذه المحاكاة للتنبؤ، من الناحية النوعية، بكيفية تأثير قوة خارجية على سرعة واتجاه حركة الجسم. اشرح التأثيرات بمساعدة مخطط الجسم الحر. استخدم مخططات الجسم الحر لرسم الرسوم البيانية للموضع والسرعة والتسارع والقوة والعكس صحيح. اشرح كيفية ارتباط الرسوم البيانية ببعضها البعض. باستخدام سيناريو أو رسم بياني، ارسم جميع الرسوم البيانية الأربعة.