4.6: الحركة النسبية في البعد الواحد والبعدين

Last updated
Save as PDF

Page ID: 200043

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

أهداف التعلم

شرح مفهوم الإطارات المرجعية.
اكتب معادلات الموضع ومتجه السرعة للحركة النسبية.
ارسم متجهات الموضع والسرعة للحركة النسبية.
قم بتحليل مشاكل الحركة النسبية أحادية البعد وثنائية الأبعاد باستخدام معادلات الموضع ومتجه السرعة.

لا تحدث الحركة بمعزل عن غيرها. إذا كنت تركب قطارًا يتحرك بسرعة ١٠ م/ث شرقًا، فسيتم قياس هذه السرعة بالنسبة إلى الأرض التي تسافر عليها. ومع ذلك، إذا مر بك قطار آخر بسرعة 15 متر/ثانية شرقًا، فإن سرعتك بالنسبة إلى هذا القطار الآخر تختلف عن سرعتك بالنسبة إلى الأرض. سرعتك بالنسبة إلى القطار الآخر هي 5 م/ث غربًا. لاستكشاف هذه الفكرة بشكل أكبر، نحتاج أولاً إلى وضع بعض المصطلحات.

إطارات مرجعية

لمناقشة الحركة النسبية في بُعد واحد أو أكثر، نقدم أولاً مفهوم الإطارات المرجعية. عندما نقول أن الجسم له سرعة معينة، يجب أن نذكر أنه يحتوي على سرعة فيما يتعلق بإطار مرجعي معين. في معظم الأمثلة التي فحصناها حتى الآن، كان هذا الإطار المرجعي هو الأرض. إذا قلت إن شخصًا يجلس في قطار يتحرك بسرعة 10 م/ث شرقًا، فأنت تشير إلى أن الشخص على متن القطار يتحرك بالنسبة إلى سطح الأرض بهذه السرعة، والأرض هي الإطار المرجعي. يمكننا توسيع نظرتنا لحركة الشخص على متن القطار ونقول أن الأرض تدور في مدارها حول الشمس، وفي هذه الحالة تصبح الحركة أكثر تعقيدًا. في هذه الحالة، يكون النظام الشمسي هو الإطار المرجعي. باختصار، يجب أن تحدد جميع مناقشات الحركة النسبية الأطر المرجعية المعنية. نقوم الآن بتطوير طريقة للإشارة إلى الإطارات المرجعية في الحركة النسبية.

الحركة النسبية في بُعد واحد

نقدم الحركة النسبية في بُعد واحد أولاً، لأن متجهات السرعة تبسط وجود اتجاهين ممكنين فقط. خذ مثال الشخص الجالس في قطار يتجه شرقًا. إذا اخترنا الشرق باعتباره الاتجاه الإيجابي والأرض كإطار مرجعي، فيمكننا كتابة سرعة القطار فيما يتعلق بالأرض كـ$\vec{v}_{TE}$ = 10 م/ث$\hat{i}$ شرقًا، حيث تشير المقتطفات TE إلى القطار والأرض. لنفترض الآن أن الشخص نهض من مقعده وسار باتجاه مؤخرة القطار بسرعة 2 متر/ثانية، وهذا يخبرنا أن سرعته تتناسب مع الإطار المرجعي للقطار. بما أن الشخص يسير غربًا، في الاتجاه السالب، نكتب سرعته بالنسبة إلى القطار كما$\vec{v}_{PT}$ = −2 م/ث$\hat{i}$. يمكننا إضافة متجهي السرعة لإيجاد سرعة الشخص بالنسبة للأرض. تتم كتابة هذه السرعة النسبية كـ

\[\vec{v}_{PE} = \vec{v}_{PT} + \vec{v}_{TE} \ldotp \label{4.33}\]

لاحظ ترتيب النقاط الفرعية للإطارات المرجعية المختلفة في المعادلة\ ref {4.33}. تظهر رموز الإطار المرجعي للاقتران، وهو القطار، بشكل متتابع في الجانب الأيمن من المعادلة. $\PageIndex{1}$يوضح الشكل الترتيب الصحيح للنقاط الفرعية عند تكوين معادلة المتجهات.

بديل — الشكل$\PageIndex{1}$: عند إنشاء معادلة المتجهات، تظهر الرموز الفرعية للإطار المرجعي للاقتران على التوالي من الداخل. إن الرموز الفرعية الموجودة على الجانب الأيسر من المعادلة هي نفس النقطتين الخارجيتين على الجانب الأيمن من المعادلة.

عند جمع المتجهات، نجد$\vec{v}_{PE}$ = 8 م/ث$\hat{i}$، بحيث يتحرك الشخص 8 م/ث شرقًا بالنسبة إلى الأرض. من الناحية الرسومية، يظهر هذا في الشكل$\PageIndex{2}$.

متجهات سرعة القطار فيما يتعلق بالأرض والشخص فيما يتعلق بالقطار والشخص فيما يتعلق بالأرض. V sub T E هو متجه سرعة القطار فيما يتعلق بالأرض. تبلغ قيمته 10 أمتار في الثانية ويتم تمثيله كسهم أخضر طويل يشير إلى اليمين. V sub P T هو متجه السرعة للشخص فيما يتعلق بالقطار. تبلغ قيمته -2 متر في الثانية ويتم تمثيله كسهم أخضر قصير يشير إلى اليسار. V sub P E هو متجه السرعة للشخص فيما يتعلق بالأرض. تبلغ قيمته 8 أمتار في الثانية ويتم تمثيله كسهم أخضر متوسط الطول يشير إلى اليمين. — الشكل$\PageIndex{2}$: متجهات سرعة القطار فيما يتعلق بالأرض، والشخص فيما يتعلق بالقطار، والشخص فيما يتعلق بالأرض.

السرعة النسبية في بعدين

يمكننا الآن تطبيق هذه المفاهيم لوصف الحركة في بعدين. ضع في اعتبارك الجسيم P والإطاران المرجعيان S و S ′، كما هو موضح في الشكل$\PageIndex{3}$. موضع أصل S ′ كما تم قياسه في S هو$\vec{r}_{S'S}$، موضع P كما تم قياسه في S ′$\vec{r}_{PS'}$، وموضع P كما تم قياسه في S هو$\vec{r}_{PS}$.

يتم عرض نظام إحداثيات x y z وتسميته باسم النظام S. يتم تحويل نظام الإحداثيات الثاني، S Prime مع المحاور x Prime و y Prime و z Prime، بالنسبة إلى S. ويمتد المتجه r sub S Prime S، الموضح كسهم أرجواني، من أصل S إلى أصل S. المتجه r sub P S هو متجه من أصل S إلى نقطة P. Vector r sub P S Prime هو متجه من أصل S Prime إلى نفس النقطة P. تشكل المتجهات r s prime s و r P S Prime و r P S مثلثًا، و r P S هو مجموع متجه r S Prime S و r P S Prime. — الشكل$\PageIndex{3}$: مواضع الجسيم P بالنسبة للإطارات S و S ′ هي$\vec{r}_{PS}$ و$\vec{r}_{PS'}$، على التوالي.

من الشكل$\PageIndex{3}$ نرى ذلك

\[\vec{r}_{PS} = \vec{r}_{PS} + \vec{r}_{S'S} \ldotp \label{4.34}\]

السرعات النسبية هي المشتقات الزمنية لمتجهات الموضع. لذلك،

\[\vec{v}_{PS} = \vec{v}_{PS'} + \vec{v}_{S'S} \ldotp \label{4.35}\]

سرعة الجسيم بالنسبة إلى S تساوي سرعته بالنسبة إلى S ′ بالإضافة إلى سرعة S بالنسبة إلى S.

يمكننا توسيع المعادلة\ ref {4.35} إلى أي عدد من الإطارات المرجعية. بالنسبة للجسيم P ذي السرعات$\vec{v}_{PA}$$\vec{v}_{PB}$،$\vec{v}_{PC}$ وفي الإطارات A و B و C،

\[\vec{v}_{PC} = \vec{v}_{PA} + \vec{v}_{AB} + \vec{v}_{BC} \ldotp \label{4.36}\]

يمكننا أيضًا معرفة كيفية ارتباط التسرعات كما لوحظ في إطارين مرجعيين عن طريق تمييز المعادلة\ ref {4.35}:

\[\vec{a}_{PS} = \vec{a}_{PS'} + \vec{a}_{S'S} \ldotp \label{4.37}\]

نرى أنه إذا كانت سرعة S ′ بالنسبة إلى S ثابتة، فعندئذٍ$\vec{a}_{S'S}$ = 0 و

\[\vec{a}_{PS} = \vec{a}_{PS'} \ldotp \label{4.38}\]

يشير هذا إلى أن تسارع الجسيم هو نفسه الذي تم قياسه بواسطة مراقبين يتحركان بسرعة ثابتة بالنسبة لبعضهما البعض.

مثال 4.13: حركة سيارة بالنسبة إلى الشاحنة

تسير شاحنة جنوبًا بسرعة ٧٠ كم/ساعة في اتجاه أحد التقاطعات. تسير سيارة شرقًا باتجاه التقاطع بسرعة ٨٠ كم/ساعة (الشكل$\PageIndex{4}$). ما سرعة السيارة بالنسبة للشاحنة؟

تظهر شاحنة تسير جنوبًا بسرعة V الفرعية T E البالغة 70 كم/ساعة باتجاه أحد التقاطعات. تسير سيارة شرقًا باتجاه التقاطع بسرعة V دون C E تبلغ 80 كم/ساعة — الشكل$\PageIndex{4}$: تسير سيارة شرقًا نحو التقاطع بينما تتحرك الشاحنة جنوبًا نحو نفس التقاطع.

إستراتيجية

أولاً، يجب علينا إنشاء الإطار المرجعي المشترك لكلتا السيارتين، وهو الأرض. ثم نكتب سرعات كل منها فيما يتعلق بالإطار المرجعي للأرض، مما يمكننا من تكوين معادلة متجهية تربط السيارة والشاحنة والأرض لحل سرعة السيارة بالنسبة للشاحنة.

الحل

تبلغ سرعة السيارة بالنسبة للأرض$\vec{v}_{CE}$ = 80 كم/ساعة$\hat{i}$. تبلغ سرعة الشاحنة بالنسبة للأرض$\vec{v}_{TE}$ = −70 كم/ساعة$\hat{j}$. باستخدام قاعدة جمع السرعة، فإن معادلة الحركة النسبية التي نسعى إليها هي

\[\vec{v}_{CT} = \vec{v}_{CE} + \vec{v}_{ET} \ldotp \label{ex2}\]

هنا،$\vec{v}_{CT}$ سرعة السيارة بالنسبة للشاحنة، والأرض هي الإطار المرجعي المتصل. نظرًا لأن لدينا سرعة الشاحنة فيما يتعلق بالأرض، فإن سالب هذا المتجه هو سرعة الأرض بالنسبة للشاحنة:$\vec{v}_{ET} = − \vec{v}_{TE}$. يظهر الرسم التخطيطي للمتجه لهذه المعادلة في الشكل$\PageIndex{5}$.

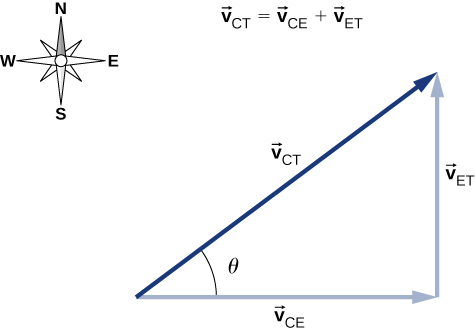
يظهر المثلث الأيمن المتكون من المتجهات V sub C E إلى اليمين، V sub E T لأسفل، V sub C T لأعلى ولليمين V sub C T لأعلى ولليمين V sub C T هو الوتر ويجعل زاوية ثيتا مع V sub C E. يُعطى متجه معادلة المتجهات v sub C T يساوي المتجه C E زائد المتجه E. تظهر بوصلة تشير إلى الشمال لأعلى، ومن الشرق إلى اليمين، ومن الجنوب إلى الأسفل، ومن الغرب إلى اليسار. — الشكل$\PageIndex{5}$: مخطط متجه لمعادلة المتجهات\ ref {ex2}.

يمكننا الآن حل سرعة السيارة فيما يتعلق بالشاحنة:

\[\big| \vec{v}_{CT} \big| = \sqrt{(80.0\; km/h)^{2} + (70.0\; km/h)^{2}} = 106.\; km/h \nonumber\]

\[\theta = \tan^{-1} \left(\dfrac{70.0}{80.0}\right) = 41.2^{o}\; north\; of\; east \ldotp \nonumber\]

الدلالة

يمكن أن يساعد رسم مخطط متجه يوضح متجهات السرعة في فهم السرعة النسبية للكائنين.

التمرين 4.6

يتجه قارب نحو الشمال في مياه ساكنة بسرعة ٤٫٥ م/ث مباشرةً عبر نهر يجري شرقًا بسرعة ٣٫٠ م/ث، ما سرعة القارب بالنسبة إلى الأرض؟

مثال 4.14: الطيران بالطائرة في الرياح

يجب أن يقود الطيار طائرته شمالًا للوصول إلى وجهته. يمكن للطائرة أن تطير بسرعة 300 كم/ساعة في الهواء الساكن. تهب ريح من الشمال الشرقي بسرعة ٩٠ كم/ساعة. (أ) ما سرعة الطائرة بالنسبة إلى الأرض؟ (ب) في أي اتجاه يجب أن تقود الطيارة طائرتها لتطير شمالاً؟

إستراتيجية

يجب على الطيار توجيه طائرتها إلى حد ما إلى الشرق من الشمال للتعويض عن سرعة الرياح. نحن بحاجة إلى بناء معادلة متجهة تحتوي على سرعة الطائرة بالنسبة للأرض، وسرعة الطائرة بالنسبة للهواء، وسرعة الهواء بالنسبة للأرض. نظرًا لأن هاتين الكميتين الأخيرتين معروفتان، يمكننا حل سرعة الطائرة فيما يتعلق بالأرض. يمكننا رسم المتجهات واستخدام هذا المخطط لتقييم حجم سرعة الطائرة بالنسبة إلى الأرض. سيخبرنا الرسم التخطيطي أيضًا بالزاوية التي تصنعها سرعة الطائرة مع الشمال فيما يتعلق بالهواء، وهو الاتجاه الذي يجب أن يقود الطيار طائرته.

الحل

معادلة المتجهات هي$\vec{v}_{PG} = \vec{v}_{PA} + \vec{v}_{AG}$، حيث P = المستوى، A = الهواء، و G = الأرض. من خلال الشكل الهندسي في الشكل$\PageIndex{6}$، يمكننا بسهولة حل حجم سرعة الطائرة فيما يتعلق بالأرض وزاوية اتجاه الطائرة$\theta$.

تُظهر البوصلة الشمال لأعلى، ومن الشرق إلى اليمين، ومن الجنوب إلى الأسفل، ومن الغرب إلى اليسار. تشكل المتجهات V الفرعية P G و V الفرعية A G و V الفرعية P A مثلثًا. تظهر طائرة على المتجه V الفرعي P G، الذي يشير لأعلى. يشير V sub P A إلى الأعلى وإلى اليمين، بزاوية من ثيتا إلى متجه V الفرعي P G يشير إلى الأسفل وإلى اليسار، بزاوية 45 درجة تحت الأفقي. V sub P G هو مجموع المتجهات لـ v sub P A و V sub A G. — الشكل$\PageIndex{6}$: مخطط متجه للمعادلة\ ref {4.34} يوضح المتجهات$\vec{v}_{PA}$$\vec{v}_{AG}$ و$\vec{v}_{PG}$.

الكميات المعروفة: $\ big|\ vec {v} _ {PA}\ big| = 300\; كلم/ساعة $$$/big|\ vec {v} _ {AG}\ big| = 90\; كم/ساعة $استبدال معادلة الحركة، نحصل على$\big| \vec{v}_{PG} \big|$ = 230 كم/ساعة.
الزاوية$\theta$ = تان ⁻¹$\left(\dfrac{63.64}{300}\right)$ = 12 درجة شرق الشمال.