4.5: حركة دائرية موحدة

Last updated
Save as PDF

Page ID: 200044

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

أهداف التعلم

حل التسارع المركزي لجسم يتحرك على مسار دائري.
استخدم معادلات الحركة الدائرية لإيجاد موضع الجسم الذي ينفّذ حركة دائرية وسرعته وعجلته.
اشرح الاختلافات بين التسارع المركزي والتسارع العرضي الناتج عن الحركة الدائرية غير المنتظمة.
قم بتقييم التسارع المركزي والتسارع العرضي في الحركة الدائرية غير المنتظمة، وابحث عن متجه التسارع الكلي.

الحركة الدائرية المنتظمة هي نوع معين من الحركة التي ينتقل فيها الجسم في دائرة بسرعة ثابتة. على سبيل المثال، أي نقطة على مروحة تدور بمعدل ثابت تؤدي إلى تنفيذ حركة دائرية موحدة. ومن الأمثلة الأخرى عقرب الساعة الثاني وعقارب الدقائق وعقارب الساعة. من اللافت للنظر أن النقاط على هذه الأجسام الدوارة تتسارع بالفعل، على الرغم من أن معدل الدوران ثابت. لرؤية هذا، يجب علينا تحليل الحركة من حيث المتجهات.

تسريع الجاذبية المركزية

في علم الحركة أحادي البعد، يكون للأجسام ذات السرعة الثابتة تسارع صفري. ومع ذلك، في معادلات الحركة ثنائية وثلاثية الأبعاد، حتى لو كانت السرعة ثابتة، يمكن للجسيم أن يتسارع إذا تحرك على طول مسار منحني مثل الدائرة. في هذه الحالة يتغير متجه السرعة،\(\frac{d\vec{v}}{dt}\) أو 0. يظهر هذا في الشكل\(\PageIndex{1}\). عندما يتحرك الجسيم بعكس اتجاه عقارب الساعة في الوقت\(\Delta\) t على المسار الدائري، يتحرك متجه موضعه\(\vec{r}(t)\) من الأعلى\(\vec{r}(t + \Delta t)\). ومتجه السرعة له حجم ثابت ويكون مماسًا للمسار عندما يتغير من\(\vec{v}\) (t) إلى\(\vec{v}\left(t + \Delta t\right)\)، مع تغيير اتجاهه فقط. نظرًا\(\vec{v}(t)\) لأن متجه السرعة عمودي على متجه الموضع\(\vec{r}\) (t)، فإن المثلثات المتكونة من متجهات الموضع ومتجهات السرعة\(\Delta \vec{v}\) متشابهة.\(\Delta \vec{r}\) علاوة على ذلك، منذ

\[|\vec{r}(t) | = | \vec{r} (t + \Delta t)| \nonumber\]

\[| \vec{v} (t)| = | \vec{v} (t + \Delta t)|, \nonumber \]

المثلثان متساوي الساقين. من هذه الحقائق يمكننا التأكيد

\[\dfrac{\Delta v}{v} = \dfrac{\Delta r}{r}\]

أو

\[\Delta v = \dfrac{v}{r} \Delta r.\]

يوضح الشكل أ دائرة مركزها عند النقطة C. يظهر نصف القطر r من t ونصف القطر r ونصف القطر r لـ t، وهما الزاوية التي تفصل بينهما دلتا ثيتا، وطول الوتر دلتا r الذي يربط طرفي نصفي القطر. تشكل المتجهات r of t و r of t بالإضافة إلى دلتا t و Delta r مثلثًا. عند طرف المتجه r of t، تظهر السرعة على هيئة v من t وتشير إلى الأعلى وإلى اليمين، مماس الدائرة. عند طرف المتجه r of t زائد دلتا t، تظهر السرعة في صورة v من t زائد دلتا t وتشير إلى الأعلى وإلى اليسار، مماس الدائرة. يُظهر الشكل (ب) المتجهين v لـ t وv من t زائد دلتا t بذيولها معًا، ومتجه دلتا v من طرف v من t إلى طرف v من t زائد دلتا t، وتشكل هذه المتجهات الثلاثة مثلثًا. الزاوية بين v of t و v لـ t بالإضافة إلى دلتا t هي ثيتا. — الشكل\(\PageIndex{1}\): (أ) يتحرك الجسيم في دائرة بسرعة ثابتة، مع وجود متجهات الموضع والسرعة في بعض الأحيان\(t\) و\(t + \Delta t\). (ب) متجهات السرعة التي تشكل مثلثًا. المثلثان في الشكل متشابهان. \(\Delta \vec{v}\)يشير المتجه نحو مركز الدائرة في الحد\(\Delta t → 0.\)

يمكننا العثور على حجم التسارع من

\[a = \lim_{\Delta t \rightarrow 0} \left(\dfrac{\Delta v}{\Delta t}\right) = \frac{v}{r} \left(\lim_{\Delta t \rightarrow 0} \dfrac{\Delta r}{\Delta t}\right) = \frac{v^{2}}{r} \ldotp\]

يمكن أيضًا العثور على اتجاه التسارع من خلال ملاحظة أنه مع اقتراب\(\Delta\) t وبالتالي\(\Delta \theta\) من الصفر،\(\Delta \vec{v}\) يقترب المتجه من اتجاه عمودي على\(\vec{v}\). في الحد\(\Delta t → 0,\)\(\Delta \vec{v}\) يكون عموديًا على\(\vec{v}\). \(\vec{v}\)نظرًا لوجود مماس الدائرة، فإن التسارع\(\frac{d \vec{v}}{dt}\) يشير إلى مركز الدائرة. تلخيصًا، فإن جسيمًا يتحرَّك في دائرة بسرعة ثابتة له تسارع ذي حجم

\[a_{c} = \frac{v^{2}}{r} \ldotp \label{4.27}\]

اتجاه متجه التسارع هو مركز الدائرة (الشكل\(\PageIndex{2}\)). هذا هو التسارع الشعاعي ويسمى التسارع المركزي، ولهذا السبب نعطيه الرمز المنخفض\(c\). تأتي كلمة centripetal من الكلمات اللاتينية centrum (بمعنى «المركز») و petere (معنى البحث»)، وبالتالي تأخذ معنى «البحث عن المركز».

تظهر الدائرة بسهم أرجواني مُسمى كمتجه، وجزء فرعي c يشير شعاعيًا إلى الداخل، وسهم أخضر مماس الدائرة ومُسمى v. وتظهر الأسهم مع ذيولها في نفس النقطة على الدائرة. — الشكل\(\PageIndex{2}\): يشير متجه التسارع المركزي نحو مركز المسار الدائري للحركة وهو تسارع في الاتجاه الشعاعي. يظهر متجه السرعة أيضًا وهو مماس الدائرة.

دعونا نتحرى بعض الأمثلة التي توضح المقادير النسبية للسرعة ونصف القطر والتسارع المركزي.

مثال\(\PageIndex{1}\): Creating an Acceleration of 1 g

تحلق طائرة بسرعة ١٣٤٫١ م/ث على طول خط مستقيم وتدور على طول مسار دائري مع الأرض. ماذا يجب أن يكون نصف قطر الدائرة لإنتاج عجلة جاذبية مركزية مقدارها ١ g على الطيار وطائرة متجهة نحو مركز المسار الدائري؟

إستراتيجية

بالنظر إلى سرعة الطائرة، يمكننا حل نصف قطر الدائرة في تعبير التسارع المركزي.

الحل

اضبط تسارع الجاذبية المركزية الذي يساوي تسارع الجاذبية: 9.8 م/ث ² =\(\frac{v^{2}}{r}\).

نجد حل نصف القطر

\[r = \frac{(134.1\; m/s)^{2}}{9.8\; m/s^{2}} = 1835\; m = 1.835\; km \ldotp\]

الأهمية

لتحقيق تسارع أكبر من g على الطيار، سيتعين على الطائرة إما تقليل نصف قطر مسارها الدائري أو زيادة سرعتها على مسارها الحالي أو كليهما.

التمرين 4.5

يبلغ نصف قطر دولاب الموازنة ٢٠٫٠ سم. ما سرعة نقطة على حافة دولاب الموازنة إذا تعرضت لعجلة جاذبية مركزية مقدارها 900.0 سم/ث ²؟

يمكن أن يحتوي التسارع المركزي على نطاق واسع من القيم، اعتمادًا على سرعة ونصف قطر انحناء المسار الدائري. يتم إعطاء التسرعات المركزية النموذجية في الجدول\(\PageIndex{1}\).

الجدول\(\PageIndex{1}\): التسرعات المركزية النموذجية
الكائن	تسارع الجاذبية المركزية (م/ث ² أو عوامل g)
الأرض حول الشمس	5.93 × 10 ^-3
القمر حول الأرض	2.73 × 10 ^-3
ساتل في مدار متزامن مع الأرض	0.233
الحافة الخارجية للقرص المضغوط عند اللعب	5.75
طائرة في لفة برميل	(2-3 جرام)
السفينة الدوارة	(5 جم)
إلكترون يدور حول بروتون في نموذج بوهر البسيط للذرة	9.0 × 10 ²²

معادلات الحركة للحركة الدائرية المنتظمة

يمكن وصف الجسيم الذي ينفذ حركة دائرية بواسطة متجه موضعه\(\vec{r}(t)\). \(\PageIndex{3}\)يوضِّح الشكل جسيمًا ينفِّذ حركة دائرية في اتجاه عكس عقارب الساعة. عندما يتحرك الجسيم على الدائرة، يقوم متجه موضعه بمسح الزاوية\(\theta\) باستخدام المحور السيني. يظهر المتجه الذي\(\vec{r}(t)\) يصنع زاوية\(\theta\) مع المحور السيني بمكوناته على طول المحورين x و y. حجم متجه الموضع هو\(A = |\vec{r}(t)|\) ولا يزال أيضًا نصف قطر الدائرة، بحيث من حيث مكوناتها،

\[\vec{r} (t) = A \cos \omega \hat{i} + A \sin \omega t \hat{j} \ldotp \label{4.28}\]

هنا،\(\omega\) يوجد ثابت يسمى التردد الزاوي للجسيم. يحتوي التردد الزاوي على وحدات راديان (راد) في الثانية وهو ببساطة عدد راديان القياس الزاوي الذي يمر من خلاله الجسيم في الثانية. الزاوية\(θ\) التي يحتويها متجه الموضع في أي وقت معين هي\(\omega\) t.

\(T\)إذا كانت فترة الحركة، أو وقت إكمال ثورة واحدة (\(2 \pi\, rad\))، إذن

يظهر نصف قطر الدائرة r، المتمركز حول أصل نظام الإحداثيات x y. نصف القطر r of t هو متجه من نقطة الأصل إلى نقطة على الدائرة ويكون بزاوية ثيتا تساوي أوميغا t على الأفقي. المكون x للمتجه r هو مقدار r من t مضروبًا في جيب التمام لأوميغا t، والمكون y للمتجه r هو مقدار r من t مضروبًا في الجيب لـ omega t، ويكون الدوران عكس اتجاه عقارب الساعة حول الدائرة. — الشكل\(\PageIndex{3}\): متجه الموضع للجسيم في حركة دائرية مع مكوناته على طول المحاور x- و y. يتحرك الجسيم بعكس اتجاه عقارب الساعة. الزاوية\(\theta\) هي التردد الزاوي بالراديان\(\omega\) في الثانية مضروبًا في\(t\).

يمكن الحصول على السرعة والتسارع من دالة الموضع عن طريق التمايز:

\[\vec{v} (t) = \frac{d \vec{r} (t)}{dt} = -A \omega \sin \omega t \hat{i} + A \omega \cos \omega t \hat{j} \ldotp \label{4.29}\]

يمكن أن يظهر من الشكل\(\PageIndex{3}\) أن متجه السرعة مماس للدائرة عند موقع الجسيم، بحجم A\(\omega\). وبالمثل، يتم العثور على متجه التسارع من خلال تمييز السرعة:

\[\vec{a} (t) = \frac{d \vec{v} (t)}{dt} = -A \omega^{2} \cos \omega t \hat{i} - A \omega^{2} \sin \omega t \hat{j} \ldotp \label{4.30}\]

من هذه المعادلة نرى أن متجه التسارع له المقدار A\(\omega^{2}\) ويتم توجيهه مقابل متجه الموضع، نحو نقطة الأصل، لأن\(\vec{a}\) (t) = −\(\omega^{2} \vec{r}\) (t).

مثال\(\PageIndex{2}\): Circular Motion of a Proton

سرعة بروتون ٥ × ١٠ ^٦ م/ث ويتحرك في دائرة في المستوى xy نصف قطره r = 0.175 m، ما موضعه في المستوى xy في الوقت t = ٢٫٠ × ١٠ ^−٧ ث = ٢٠٠ نانو ثانية؟ عند t = 0، يكون موضع البروتون 0.175 m\(\hat{i}\) ويدور حول عكس اتجاه عقارب الساعة. ارسم المسار.

الحل

من البيانات المعطاة، يحتوي البروتون على فترة وتردد زاوي:

\[T = \frac{2 \pi r}{v} = \frac{2 \pi (0.175\; m)}{5.0 \times 10^{6}\; m/s} = 2.20 \times 10^{-7}\; s \nonumber \]

\[\omega = \frac{2 \pi}{T} = \frac{2 \pi}{2.20 \times 10^{-7}\; s} = 2.856 \times 10^{7}\; rad/s \ldotp \nonumber \]

موضع الجسيم عند t = 2.0 × 10 ⁻⁷ ثانية مع A = 0.175 m هو

\[\begin{align*} \vec{r} (2.0 \times 10^{-7}\; s) & = A \cos \omega (2.0 \times 10^{-7}\; s) \hat{i} + A \sin \omega (2.0 \times 10^{-7}\; s) \hat{j}\; m \\[4pt] & = 0.175 \cos (2.856 \times 10^{7}\; rad/s) (2.0 \times 10^{-7}\; s) \hat{i} + 0.175 \sin (2.856 \times 10^{7}\; rad/s) (2.0 \times 10^{-7}\; s) \hat{j}\; m \\[4pt] & = 0.175 \cos (5.712\; rad) \hat{i} + 0.175 \sin (5.172\; rad) \hat{j}\; m \\ & = 0.147 \hat{i} - 0.095 \hat{j}\; m \ldotp \end{align*}\]

من هذه النتيجة نرى أن البروتون يقع قليلاً تحت المحور السيني. يظهر هذا في الشكل\(\PageIndex{4}\).

يظهر رسم بياني لموضع y كدالة لموضع x. يتم قياس كل من x و y بالأمتار ويتم تشغيلهما من -0.2 إلى 0.2. تتحرَّك بروتون في دائرة بعكس اتجاه عقارب الساعة تتمركز حول نقطة الأصل وتُظهر في ١١ مرة مختلفة. عند t = 0 ثانية يكون الجسيم عند x = 0.175 m و y = 0. عند t = 200 نانو ثانية، يكون الجسيم في موضع يحدده المتجه 0.147 I الذي ناقص 0.95 j من عدادات الحرارة. — الشكل\(\PageIndex{4}\): متجه الموضع للبروتون عند\(t = 2.0 \times 10^{−7}\,ms = 200\, ns\). يظهر مسار البروتون. الزاوية التي ينتقل خلالها البروتون على طول الدائرة تساوي 5.712 راد، أي أقل بقليل من دورة واحدة كاملة.

الأهمية

اخترنا الموضع الأولي للجسيم ليكون على المحور السيني. كان هذا تعسفيًا تمامًا. إذا تم إعطاء موضع بداية مختلف، فسيكون لدينا موضع نهائي مختلف عند t = 200 ns.

حركة دائرية غير منتظمة

لا يجب أن تكون الحركة الدائرية بسرعة ثابتة. يمكن للجسيم أن ينتقل في دائرة ويسرع أو يبطئ، مما يُظهر تسارعًا في اتجاه الحركة.

في الحركة الدائرية المنتظمة، يكون للجسيم المنفذ للحركة الدائرية سرعة ثابتة والدائرة في نصف قطر ثابت. إذا كانت سرعة الجسيم تتغير أيضًا، فإننا نقدم تسارعًا إضافيًا في الاتجاه المماسي للدائرة. تحدث مثل هذه التسرعات عند نقطة على القمة تقوم بتغيير معدل الدوران، أو أي دوار متسارع. في متجهات الإزاحة والسرعة، أظهرنا أن التسارع المركزي هو المعدل الزمني لتغيير اتجاه متجه السرعة. إذا كانت سرعة الجسيم تتغير، فسيكون له تسارع مماسي وهو المعدل الزمني لتغيير حجم السرعة:

\[a_{T} = \frac{d |\vec{v}|}{dt} \ldotp \label{4.31}\]

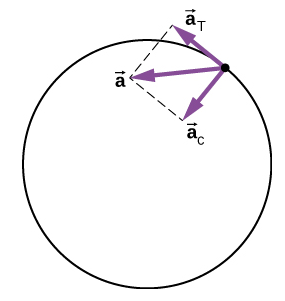
يكون اتجاه التسارع العرضي مماسًا للدائرة بينما يكون اتجاه التسارع المركزي شعاعيًا نحو الداخل باتجاه مركز الدائرة. وهكذا، فإن الجسيم في الحركة الدائرية مع التسارع العرضي له تسارع كلي يمثل المجموع المتجه للتسارع المركزي والتسارع العرضي:

\[\vec{a} = \vec{a}_{c} + \vec{a}_{T} \ldotp \label{4.32}\]

تظهر متجهات التسارع في الشكل\(\PageIndex{5}\). لاحظ أن\(\vec{a}_{c}\) متجهي التسارع\(\vec{a}_{T}\) متعامدتان مع\(\vec{a}_{c}\) بعضهما البعض،\(\vec{a}_{T}\) في الاتجاه الشعاعي وفي الاتجاه العرضي. \(\vec{a}\)نقاط التسارع الإجمالية بزاوية بين\(\vec{a}_{c}\) و\(\vec{a}_{T}\).

يظهر تسارع الجسيم على الدائرة جنبًا إلى جنب مع مكوناته الشعاعية والمتماسية. يشير التسارع المركزي a sub c شعاعيًا نحو مركز الدائرة. يكون التسارع المماسي للفرعية T مماسيًا للدائرة عند موضع الجسيم. التسارع الكلي هو مجموع المتجهات للتسارعات العرضية والجذبية، والتي تكون عمودية. — الشكل\(\PageIndex{5}\): يشير التسارع المركزي نحو مركز الدائرة. يكون التسارع العرضي مماسيًا للدائرة عند موضع الجسيم. التسارع الكلي هو مجموع المتجهات للتسارعات العرضية والجذبية، والتي تكون عمودية.

مثال\(\PageIndex{3}\): Total Acceleration during Circular Motion

يتحرك جسم في دائرة نصف قطرها r = 2.0 m، وخلال الفترة الزمنية من t = 1.5 ثانية إلى t = 4.0 ثانية، تختلف سرعته بمرور الوقت وفقًا لـ

\[v(t) = c_{1} - \frac{c_{2}}{t^{2}}, c_{1} = 4.0\; m/s, c_{2} = 6.0\; m \cdotp s \ldotp\]

ما التسارع الكلي للجسيم عند t = 2.0 s؟

إستراتيجية

يتم إعطاؤنا سرعة الجسيم ونصف قطر الدائرة، حتى نتمكن من حساب تسارع الجاذبية المركزية بسهولة. اتجاه التسارع المركزي هو نحو مركز الدائرة. نجد مقدار العجلة المماسية بأخذ المشتق بالنسبة إلى زمن |v (t) | باستخدام المعادلة\ ref {4.31} وتقييمه عند t = 2.0 ثانية، ونستخدم هذا ومقدار العجلة الجاذزية لإيجاد العجلة الكلية.

الحل

تسارع الجاذبية المركزية هو

\[v(2.0\; s) = \left(4.0 - \dfrac{6.0}{(2.0)^{2}}\right) m/s = 2.5\; m/s \nonumber \]

\[a_{c} = \frac{v^{2}}{r} = \frac{(2.5\; m/s)^{2}}{2.0\; m} = 3.1\; m/s^{2} \nonumber \]

موجهة نحو مركز الدائرة. التسارع العرضي هو

\[a_{T} = \Big| \frac{d \vec{v}}{dt} \Big| = \frac{2 c_{2}}{t^{3}} = \frac{12.0}{(2.0)^{3}} m/s^{2} = 1.5\; m/s^{2} \ldotp \nonumber \]

التسارع الكلي هو

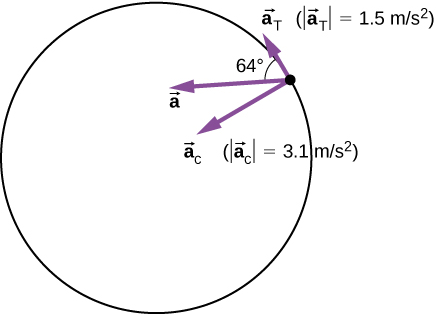
\[|\vec{a}| = \sqrt{3.1^{2} + 1.5^{2}} m/s^{2} = 3.44\; m/s^{2}\]

و\(\theta\) = تان ⁻¹\(\left(\dfrac{3.1}{1.5}\right)\) = 64° من المماس إلى الدائرة. انظر الشكل\(\PageIndex{6}\).

alt= يظهر تسارع الجسيم على الدائرة جنبًا إلى جنب مع مكوناته الشعاعية والمتماسية. يشير التسارع المركزي (a sub-c) شعاعيًا نحو مركز الدائرة وتبلغ قوته 3.1 مترًا في الثانية مربعة. التسارع العرضي للفرعية T يكون مماسيًا للدائرة عند موضع الجسيم وتبلغ قوته 1.5 متر في الثانية المربعة. الزاوية بين التسارع الكلي a والتسارع العرضي للفرعية T هي 64 درجة.» — الشكل\(\PageIndex{6}\): ناقلات التسارع العرضي والجذبي. التسارع الصافي\(\vec{a}\) هو مجموع المتجهات للتسارعين.

الأهمية

يمكن وصف اتجاهات التسارع المركزي والتماسي بشكل أكثر ملاءمة من حيث نظام الإحداثيات القطبية، مع وجود متجهات الوحدة في الاتجاهين الشعاعي والمماسي. تتم مناقشة نظام الإحداثيات هذا، المستخدم للحركة على طول المسارات المنحنية، بالتفصيل لاحقًا في الكتاب.